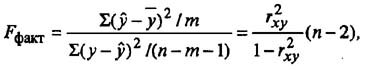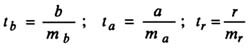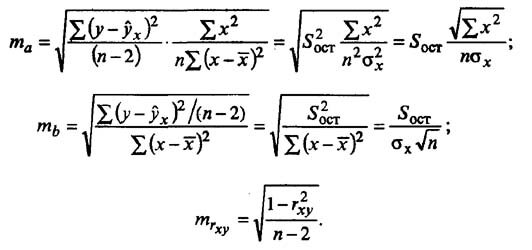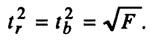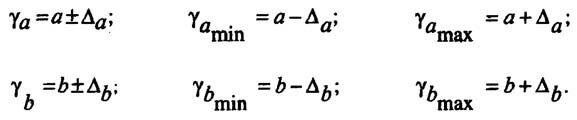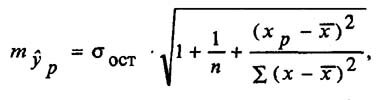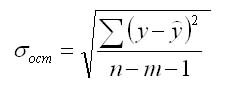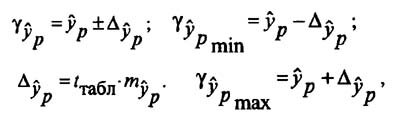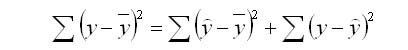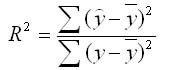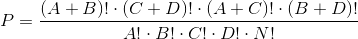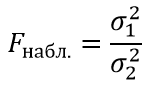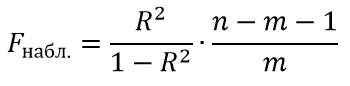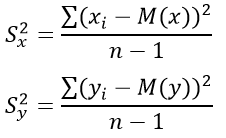Что такое критерий фишера
Критерий Фишера и Стьюдента
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
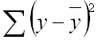
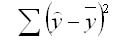
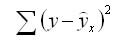
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Любые задачи по эконометрике решаются здесь
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА
– это критерий, который используется для сравнения двух и более относительных показателей, характеризующих частоту определенного признака, имеющего два значения. Исходные данные для расчета точного критерия Фишера обычно группируются в виде четырехпольной таблицы, но могут быть представлены и многопольной таблицей.
1. История разработки критерия
Впервые критерий был предложен Рональдом Фишером в его книге «Проектирование экспериментов». Это произошло в 1935 году. Сам Фишер утверждал, что на эту мысль его натолкнула Муриэль Бристоль. В начале 1920-х годов Рональд, Муриэль и Уильям Роуч находились в Англии на опытной сельскохозяйственной станции. Муриэль утверждала, что может определить, в какой последовательности наливали в ее чашку чай и молоко. На тот момент проверить правильность ее высказывания не представлялось возможным.
Это дало толчок идее Фишера о «нуль гипотезе». Целью стала не попытка доказать, что Муриэль может определить разницу между по-разному приготовленными чашками чая. Решено было опровергнуть гипотезу, что выбор женщина делает наугад. Было определено, что нуль-гипотезу нельзя ни доказать, ни обосновать. Зато ее можно опровергнуть во время экспериментов.
Было приготовлено 8 чашек. В первые четыре налито молоко сначала, в другие четыре – чай. Чашки были помешаны. Бристоль предложили опробовать чай на вкус и разделить чашки по методу приготовления чая. В результате должно было получиться две группы. История говорит, что эксперимент прошел удачно.
Благодаря тесту Фишера вероятность того, что Бристоль действует интуитивно, была уменьшена до 0.01428. То есть, верно определить чашку можно было в одном случае из 70. Но все же нет возможности свести к нулю шансы того, что мадам определяет случайно. Даже если увеличивать число чашек.
Эта история дала толчок развитию «нуль гипотезы». Тогда же был предложен точный критерий Фишера, суть которого в переборе всех возможных комбинаций зависимой и независимой переменных.
2. Для чего используется точный критерий Фишера?
Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений.
Особое место отводится точному критерию Фишера в медицине. Это важный метод обработки медицинских данных, нашедший свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь определенных фактора и исхода, сравнивать частоту патологических состояний между разными группами пациентов и т.д.
3. В каких случаях можно использовать точный критерий Фишера?
Аналогом точного критерия Фишера является Критерий хи-квадрат Пирсона, при этом точный критерий Фишера обладает более высокой мощностью, особенно при сравнении малых выборок, в связи с чем в этом случае обладает преимуществом.
4. Как рассчитать точный критерий Фишера?
Вначале составляем четырехпольную таблицу сопряженности:
| Исход есть (Наличие ВПР) | Исхода нет (Отсутствие ВПР) | Всего | |
| Фактор риска есть (Курящие) | A = 10 | B = 70 | (A + B) = 80 |
| Фактор риска отсутствует (Некурящие) | C = 2 | D = 88 | (C + D) = 90 |
| Всего | (A + C) = 12 | (B + D) = 158 | (A + B + C + D) = 170 |
Точный критерий Фишера рассчитывается по следующей формуле:
В результате вычислений находим, что P = 0,0137.
5. Как интерпретировать значение точного критерия Фишера?
Достоинством метода является соответствие полученного критерия точному значению уровня значимости p. То есть, полученное в нашем примере значение 0,0137 и есть уровень значимости различий сравниваемых групп по частоте развития ВПР плода. Необходимо лишь сопоставить данное число с критическим уровнем значимости, обычно принимаемым в медицинских исследованиях за 0,05.
Критерий Фишера
Критерий Фишера используют в качестве проверке равенства (однородности) дисперсий двух выборок, в том числе проверки значимости модели регрессии.
Критерий Фишера находится по формуле:
σ1 – большая дисперсия выборки;
σ2 – меньшая дисперсия выборки.
Формула критерий Фишера для оценки значимости уравнения регрессии:
Число степеней свободы исправленных дисперсий находятся по формулам:
для первой выборки
для второй выборки
Пример
Дана выборка успеваемости по двум группам.
| № п/п | X | Y |
| 1 | 34 | 45 |
| 2 | 44 | 68 |
| 3 | 97 | 76 |
| 4 | 62 | 56 |
| 5 | 39 | 78 |
| 6 | 73 | 64 |
| 7 | 42 | 84 |
| 8 | 95 | 54 |
| 9 | 35 | 81 |
| 10 | 37 | 79 |
| 11 | 45 | 41 |
| 12 | 43 | 47 |
| 13 | 73 | 79 |
| 14 | 53 | 32 |
| 15 | 32 | 44 |
Требуется определить различия в оценках между двумя группами при α = 0.05.
Решение
Вычислим дисперсию по X и по Y
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 34 | 45 | 42,684 | 31,609 |
| 2 | 44 | 68 | 10,24 | 4,1798 |
| 3 | 97 | 76 | 209,28 | 22,195 |
| 4 | 62 | 56 | 7,84 | 3,8242 |
| 5 | 39 | 78 | 23,684 | 28,92 |
| 6 | 73 | 64 | 41,818 | 0,5057 |
| 7 | 42 | 84 | 14,951 | 54,432 |
| 8 | 95 | 54 | 190,44 | 6,876 |
| 9 | 35 | 81 | 38,44 | 40,676 |
| 10 | 37 | 79 | 30,618 | 32,617 |
| 11 | 45 | 41 | 8,2178 | 48,38 |
| 12 | 43 | 47 | 12,484 | 24,558 |
| 13 | 73 | 79 | 41,818 | 32,617 |
| 14 | 53 | 32 | 0,04 | 99,113 |
| 15 | 32 | 44 | 51,84 | 35,469 |
| Сумма | 804 | 928 | 724,4 | 465,97 |
| Среднее | 53,6 | 61,867 |
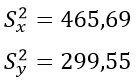
По критерию Фишера находим Fэмп. 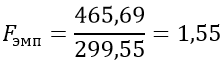
k1=15 — 1 = 14,
k2=15 — 1 = 14
По таблице критерия Фишера находим критическое значение
Fкрит=2.49, следовательно, 2.49>1.55, Fкрит>Fэмп
Отсюда, различия в оценках между двумя выборками групп присутствует, принимаем гипотезу.
F-тест качества спецификации множественной регрессионной модели
Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.
1. Роль степеней свободы (degree of freedom) в статистике
Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:
Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:
А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).
Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.
Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено
. Для оценки мы используем 2 параметра
, а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод
Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.
В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:
2. Анализ дисперсии, F-тест
При выполнении основных предположений линейной регрессии имеет место формула:
где ,
,
В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .
Масштабируем SSE и SSR с учетом их степеней свободы:
Получены хи-квадрат распределения. F-статистика вычисляется по формуле:
Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе
в случае линейной регрессионной модели вида (1).
3. Выбор линейной регрессионной модели
Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.
Определим “полную” модель: (10)
Определим “укороченную” модель: (11)
Вычисляем сумму квадратов ошибок для каждой модели:
(12)
(13)
Определяем количество степеней свобод
(14)
Коэффициент детерминации из формулы (6):
Из формулы (15) выразим SSE(F):
SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:
Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.
Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.
3 Проверка значимости линейной регрессии
Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид
. Следовательно
. Используя формулу (14.в), получим
Заключение
Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.
Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.
Надеюсь вам было интересно, спасибо за внимание.
При выводе формул очень помогли некоторые главы из курса по статистике STAT 501