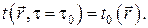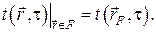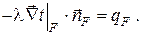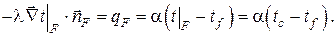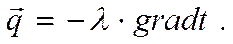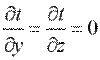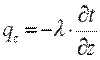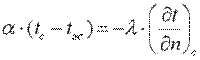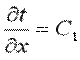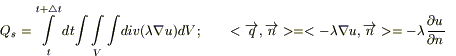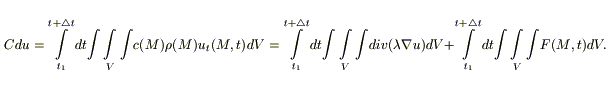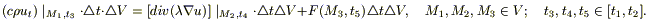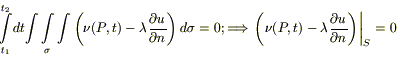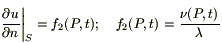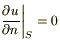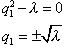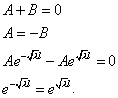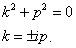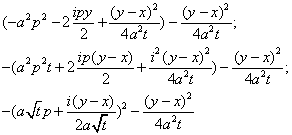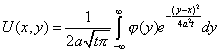Что такое краевые условия теплообмена
Краевые условия для уравнения теплопроводности
Дифференциальное уравнение теплопроводности в однородных изотропных средах в терминах математической физики есть неоднородное дифференциальное уравнение в частных производных параболического типа (первого порядка по времени и второго порядка по пространственным координатам). Если внутренние тепловыделения 
Как бы то ни было, любое дифференциальное уравнение может дать однозначное решение только если заданы условия однозначности. В случае дифференциального уравнения параболического типа должно быть задано начальное условие
Что касается граничных условий, то-есть условий теплообмена на границе рассматриваемого объёма с окружающей (контактирующей с ним) средой, то здесь имеют место несколько (а именно, четыре) возможностей, каждая из которых характеризует тот или иной тип теплового взаимодействия с внешней средой. Эти возможности обычно нумеруются римскими цифрами. Перечислим их.
I. Граничные условия I рода
В этом случае задаётся распределение температур на физической границе рассматриваемого объёма, т.е. задаётся функция координат поверхности и времени
II. Граничные условия II рода
Задаётся плотность теплового потока на границе рассматриваемого тела, что позволяет записать
Такие граничные условия обычно имеют место при решении задач теплопроводности в твёрдых телах с теплообменом излучением на границах. Чаще всего такие задачи возникают при решении задач в металлургической теплотехнике, в астрофизике и т.д.
III. Граничные условия III рода
Граничные условия III рода наиболее распространены при решении задач теплопроводности в энергетике, в металлургии и в химической технологии.
Граничные условия III рода описывают в математической форме условия теплообмена внешней поверхности твёрдого тела с контактирующей с ним жидкостью или газом, т.е. со средами, допускающими конвективные движения с перемешиванием.
Математическая формулировка граничных условий III рода базируется на гипотезе (законе) Ньютона-Рихмана, согласно которой тепловой поток с поверхности к омывающей её жидкости пропорционален разности температур, т.е.
Здесь 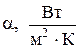
Экспериментальное обоснование гипотезы Ньютона-Рихмана состоит в том, что, как показывают экспериментальные исследования, количество теплоты, снимаемое с поверхности твёрдого тела, прямо пропорционально поверхности и разности температур поверхности и жидкости вдали от неё (как говорят, в ядре потока). Нахождение величины коэффициента теплоотдачи 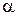
IV. Граничные условия IV рода
Граничные условия IV рода задают условия теплообмена на границе контакта твёрдых поверхностей. В частности, если контакт твёрдых поверхностей неидеален, то на границе их контакта в математическом смысле будет иметь место скачок температуры 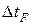
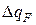
Краевые условия — Начальные и граничные условия




Краевые условия
геометрию и размеры тела, физические параметры среды и тела, граничные условия, которые характеризуют распределение температуры на поверхности тела, или взаимодействие между высвобождающимнениями, обеспечивают полное описание конкретного процесса теплопередачи
ся телом и окружающей средой. Все эти особенности, наряду с дифференциальными урав Людмила Фирмаль
и называются условиями уникальности или граничными условиями. Обычно начальное условие распределения температуры указывается для времени t = 0. * Граничные условия можно указывать тремя способами. Первый тип граничного условия определяется распределением температуры на поверхности тела в определенный момент. Второй тип граничного условия зависит от плотности
теплового потока в каждой точке поверхности тела в любой данный момент. •. Третий тип граничного условия зависит от температуры среды, окружающей тело, и закона теплообмена между поверхностью тела и окружающей средой. Закон конвективного теплообмена между поверхностью тела и окружающей средой очень сложен и будет обсуждаться в специальном разделе курса. Исследование
между поверхностью тела и окружающей средой. «Он численно равен количеству тепла, выделяемого (или воспринимаемого) поверхностными единицами за единицу времени, когда разность температур между поверхностью тела и окружающей средой составляет 1 °. Коэффициент теплопередачи зависит от многих
выделяемого (или воспринимаемого) Людмила Фирмаль
факторов, но почти всегда принимается в качестве константы при решении твердых задач теплопроводности. «% Согласно Закону о сохранении энергии количество тепла, поступающего в окружающую среду в единицу времени от единицы поверхности тела к окружающей среде в результате теплообмена, представляет собой тепло, передаваемое в единицу поверхности за единицу времени за
счет теплопроводности изнутри тела. Должен быть равным. (22-14) Где (dIdp) pop — проекция градиента температуры в нормальном направлении участка. dF \ index «pov» указывает, что градиент температуры относится к поверхности тела (n = 0). Уравнение (22-14) представляет собой математическую формулировку граничного условия третьего типа и действует в каждый момент. Решая
уравнение дифференциальной теплоты при заданном условии уникальности, вы можете определить температурное поле всего тела или найти функцию в любой момент. t = f (x, y \ z, m). Секретные вопросы в главе XXII I. Каковы основные случаи теплопередачи? • 2. Подробное объяснение всех видов теплопередачи. 3. Что такое конвективный теплообмен? 4. Какова природа лучистой энергии и
теплопроводность различных веществ. 14. Вывод дифференциального уравнения теплопроводности. 15. Уравнение Фурье для трехмерного температурного поля. 16. Что называется температуропроводностью? 17. Какие величины определяют граничные условия типа 1, типа 2 и типа 3? 18.- Закон № Ньютон-Ричман. 19. Каков коэффициент теплопередачи? Лучевая?
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
ЛЕКЦИЯ «ОСНОВЫ ТЕОРИИ ТЕПЛООБМЕНА»
ЛЕКЦИЯ «ОСНОВЫ ТЕОРИИ ТЕПЛООБМЕНА»
1. Температурное поле.
2. Градиенты температур.
3. Основой закон теплопроводности.
4. Дифференциальное уравнение теплопроводности.
ОСНОВЫ ТЕОРИИ ТЕПЛООБМЕНА
Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:
• теплопроводностью;
• конвекцией;
• излучением (радиацией).
Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.
Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностьюСостояние сухого насыщенного пара определяется одним параметром.
Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией).
Совокупность всех трех видов теплообмена называется сложным теплообменом.
ТЕМПЕРАТУРНОЕ ПОЛЕ. ТЕПЛОВОЙ ПОТОК.
Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:
Температурное поле, которое изменяется во времени, называется нестационарным (неустановившемся).
В стационарном (установившемся) температурном поле температуры разных точек тела могут быть разными, но не изменяющимися во времени.
Уравнение стационарного температурного поля :
Т= f(x,y,z).
Графически температурное поле изображают посредством изотермических поверхностей, под которыми понимается геометрическое место точек с одинаковой температурой.
Кривые, образующиеся в результате пересечения изотермической поверхности и плоскости, называются изотермами
Градиенты температур
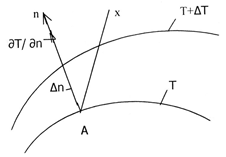
Предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn, когда Δn стремится к нулю, называют градиентом температуры
Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормали n:
Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону увеличения температуры и численно равный частной производной от температуры по этому направлению.
За положительное направление градиента принимается направление возрастания
температур, его размерность °С/м
Тепловой поток
Количество теплоты, переносимой за единицу времени через произвольную изотермическую поверхность площадью F, называется тепловым потоком Q.
Единицей измерения которого служит ватт(вт).
Тепловой поток, отнесённый к единице поверхности,называется плотностью теплового потока, или удельным тепловым потоком,
Единицей измерения q является ватт на квадратный метр (вт/м2).
Связь между Q и q устанавливается из определений:
Если тепловой поток отнесен к единице изотермической поверхности, то величина q является вектором, направление которого совпадает с направлением распространения тепла в данной точке и противоположно направлению вектора температурного градиента.
ЗАКОН ФУРЬЕ
Температуры.
Количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространения тепла.
Математическое выражение закона Фурье для плотности теплового потока имеет вид:
где λ называют коэффициентом теплопроводности
Плотность теплового потока q – векторная величина. Вектор q направлен в сторону уменьшения температуры. Знак минус в уравнении отражает противоположность направлений векторов плотности теплового потока и температурного градиента.
ГРАНИЧНЫЕ УСЛОВИЯ
Математическую формулировку частных особенностей явления называют краевыми условиями или условиями однозначности.
Различают три рода таких условий:
1) граничные условия первого рода – на поверхности тела задано распределение температуры Тп в каждый момент времени;
2) граничные условия второго рода – на поверхности тела задано распределение плотности теплового потока qп в каждый момент времени.
3) граничные условия третьего рода – известна (задана) температура окружающей тело среды и закон теплоотдачи между поверхностью тела и окружающей средой
В основу изучения конвективного теплообмена положен закон Ньютона:
Тст – температура поверхности тела (стенки), К;
Тж – температура окружающей среды (жидкости или газа), К;
α – коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м 2 ∙К).
Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.
Он численно равен количеству теплоты, отдаваемой (или воспринимаемой) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в 1 С.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется температурным полем?
2. Напишите уравнение температурного поля при нестационарном (неустановившемся) тепловом режиме.
3. Напишите уравнение температурного поля при стационарном режиме.
4. Что называется изотермической поверхностью и изотермой?
5. Что называется градиентом температуры?
6. Что называется плотностью теплового потока?
7. Напишите математическое выражение закона Фурье.
Что называется коэффициентом теплопроводности?
8. От каких факторов зависит коэффициент теплопроводности?
9. Опишите особенности теплопроводности различных веществ.
10. Дифференциальное уравнение теплопроводности.
11. Опишите граничные условия первого, второго и третьего рода.
12. Закон Ньютона для конвективного теплообмена.
13. Что называется коэффициентом теплоотдачи?
КОНТРОЛЬНЫЕ ТЕСТЫ
Процессы теплопроводности описываются уравнением:
а) Навье – Стокса;
б) Ньютона;
в) Планка;
*г) Фурье;
д) Кирхгофа.
Тепловой поток, передаваемый внутри твёрдого тела, пропорционален:
а) коэффициенту диффузии;
б) коэффициенту теплоотдачи;
*в) коэффициенту теплопроводности;
г) коэффициенту динамической вязкости.
Распределение температур внутри плоской стенки характеризуется:
а) логарифмической кривой;
б) параболой;
в) гиперболой;
*г) прямой линией.
Размерность плотности теплового потока равна:
а) о С/м; б) ; в) ; г) кДж/м2; * д) Вт/м2.
Передача теплоты между поверхностью твёрдого тела и жидкостью осуществляется за счёт:
а) сил тяжести;
б) теплопроводности;
*в) конвекции;
г) теплопроводности и конвекции;
д) электромагнитного взаимодействия;
Е) силы давления.
Процессом теплопередачи называется:
а) передача тепла внутри тела;
б) передача тепла за счёт теплового излучения;
*в) передача тепловой энергии от горячей среды к холодной через твёрдую стенку;
г) конвективный перенос тепла от горячего теплоносителя к твердой стенке.
Абсолютно чёрное тело:
а) полностью отражает тепловые лучи;
б) полностью пропускает тепловые лучи;
*в) полностью поглощает тепловое излучение.
Величина 1/ α называется:
а) коэффициентом теплопередачи;
*б) сопротивлением теплоотдачи;
в) термическим сопротивлением стенки;
г) коэффициентом теплопередачи;
д) коэффициентом теплоотдачи.
Для определения теплового потока между жидкостью и стенкой по формуле Ньютона необходимо знать, кроме площади поверхности нагрева и температурного перепада, следующие величины:
а) коэффициент теплопроводности;
*б) коэффициент теплоотдачи;
в) коэффициент температуропроводности;
г) коэффициент динамической вязкости;
д) коэффициент излучения.
СТАЦИОНАРНЫЙ ТЕПЛООБМЕН
В стационарных процессах теплопроводности температура в любой точке твердого тела не зависит от времени, т.е. ∂Т/∂t =0.
Ñ 2 Т = ∂ 2 Т/∂x 2 + ∂ 2 Т/∂y 2 + ∂ 2 Т/∂z 2 = 0
ЛЕКЦИЯ «ОСНОВЫ ТЕОРИИ ТЕПЛООБМЕНА»
1. Температурное поле.
2. Градиенты температур.
3. Основой закон теплопроводности.
4. Дифференциальное уравнение теплопроводности.
ОСНОВЫ ТЕОРИИ ТЕПЛООБМЕНА
Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:
• теплопроводностью;
• конвекцией;
• излучением (радиацией).
Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.
Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностьюСостояние сухого насыщенного пара определяется одним параметром.
Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией).
Совокупность всех трех видов теплообмена называется сложным теплообменом.
уравнение теплопроводности. поток тепла. коэффициенты теплопроводности и температуропроводности. Начальное условие



ЧАСТЬ 2. ТЕПЛОМАССООБМЕН Тема 9. ТЕПЛОПРОВОДНОСТЬ
9.1.Основные понятия и определения
Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.
Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.
Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).
Конвекция осуществляется путем перемещения в пространстве неравномерно нагретых объемов среды. При этом перенос теплоты неразрывно связан с переносом самой среды.
Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.
Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.
Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.
Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.
Совместное протекание процессов теплообмена и массообменна называетсятепломассообменном.
Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.
Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:
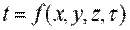
где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда
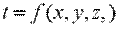
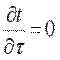
Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:
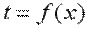
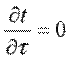
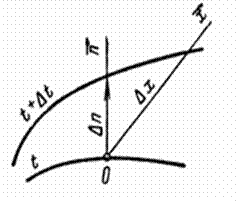
Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной 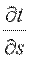
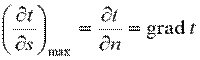
Вектор 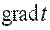
Согласно гипотезе Фурье, количество теплоты d 2 Qτ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту 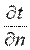
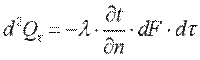
Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:
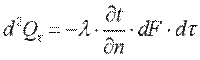
Проекции вектора q на координатные оси соответственно:
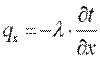
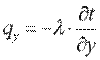
Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.
Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком: 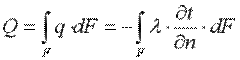
Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения 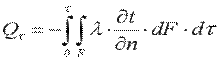
Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):
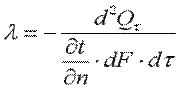
Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции
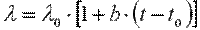
где λ0 — значение коэффициента теплопроводности при температуре t0=0 0 С; b — постоянная, определяемая опытным путем.
Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 0 С равен 0,0244 Вт/(м·К).
Для жидкости λ=0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 0 С и дальше уменьшается.
Наилучшими проводниками теплоты являются металлы, у которых λ=20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.
Материалы с λ 2 ·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду, 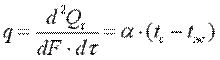
Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:
Переписав последнее уравнение в виде:
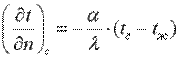
получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.
9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода
 |
| Рис. 9.2. Однородная плоская стенка |
Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры tс1 и tс2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме ( 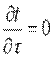
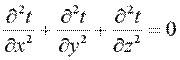
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае 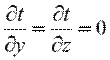
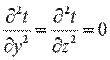
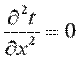
После второго интегрирования получаем 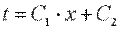
Постоянные С1 и С2 определим из граничных условий: при x=0 t=tc1, С2=tc1; приx=δ t=tc2=С1·δ+tc1, отсюда 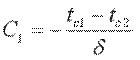
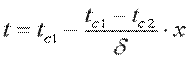
Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому 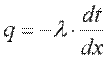
Учитывая, что 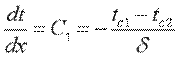
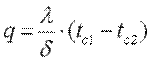
Общее количество теплоты, которое передается через поверхность стенки F за время τ,
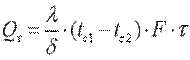
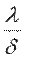
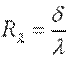
ТЕПЛОВОЙ ПОТОК — количество теплоты, переданное через изотермическую поверхность в единицу времени.
Т.П.количество теплоты, переданное через изотермическую поверхность в единицу времени. РазмерностьТ. п. совпадает с размерностью мощности (См. Мощность). Т. п. измеряется в Ваттахили ккал/ч (1 вт = 0,86ккал/ч).Т. п., отнесённый к единице изотермической поверхности, называется плотностью Т. п., удельным Т.п. или тепловой нагрузкой; обозначается обычно q, измеряется в вт/м 2 или ккал/(м 2 ․ч). Плотность Т. п. —вектор, любая компонента которого численно равна количеству теплоты, передаваемой в единицу временичерез единицу площади, перпендикулярной к направлению взятой компоненты.
Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания)температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянномдавлении, в системе СИ измеряется в м²/с.
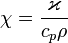
где 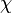
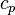
Температуропроводность и теплопроводность являются двумя из наиболее важных параметров веществ и материалов, поскольку они описывают процесс переноса теплоты и изменение температуры в них.
Величина коэффициента температуропроводности зависит от природы вещества. Жидкости и газы обладают сравнительно малой температуропроводностью. Металлы, напротив, имеют бо́льший коэффициент температуропроводности.
Коэффициент температуропроводности в тепловых процессах характеризует скорость изменения температуры. [2]
Коэффициент температуропроводности характеризует скорость выравнивания температуры ( тепловую инертность) тела и по аналогии с коэффициентом диффузии, с которым он имеет одинаковую размерность, иногда называется коэффициентом тепловой диффузии. [4]
Вывод уравнения теплопроводности:
Посмотреть определения потока и дивергенции векторного поля
1) Будем рассматривать процесс распространения тепла посредством теплопроводности (т.е. при непосредственном контакте областей с разной температурой).
2) Для теплообмена посредством теплопроводности необходимо наличие ненулевого температурного градиента, т.е. различные части тела должны иметь разную температуру. При этом, так как каждая система стремится к своему равновесному состоянию, происходит переток тепла от более «нагретых» частей тела к более «холодным».
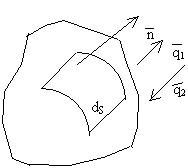
3) Для математического описания полей тепловых потоков введем в рассмотрение вектор плотности теплового потока 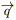
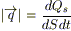
5) Будем считать, что наше изучаемое тело изотропно, т.е. λ = λ(x,y,z) и не зависит от выбора нормали к поверхности; 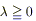
6) По определению потока для вектора 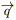
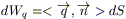
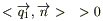
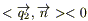
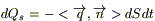
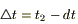
(1)
(2) 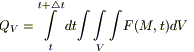
8) В соответствии с 1 м началом термодинамики тепло, получаемое системой идет на изменение ее температуры и на совершение этой системой работы: Q = Cdu + δA. Будем считать, что δA= 0 (для твердых тел).
(3) 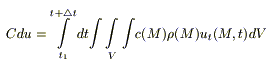
В наш выделенный объем тепло δQ поступает за счет 2 x механизмов: переноса тепла через поверхность, и возникновения тепла за счет работы источников).
Подставим (1), (2), (3):
Применим теорему о среднем значении (дважды: по t и по V) к каждому из этих интегралов:
(1) 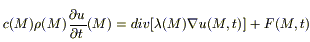
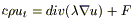
(1a) 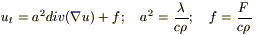
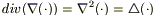
(1б) 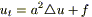
Если 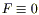
Рассмотрим теперь дополнительные условия, необходимые для однозначного решения задачи:
а) Необходимо знать начальное распределение температуры:
б) Тепловой режим на границе. Основные виды тепловых режимов:
Разберем более подробно каждый из типов:
Для записи 1 го начала термодинамики (закон сохранении энергии):
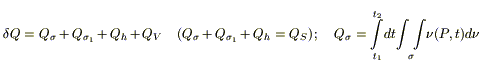
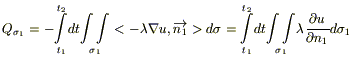
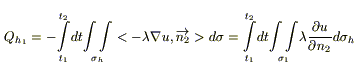
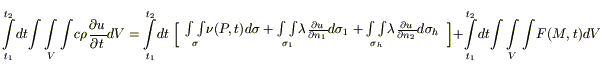
при 
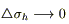
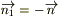
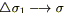
Применяя дважды теорему о среднем (по t и по σ), устремляя 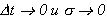
(3б)
Если поверхность S теплоизолирована (ν = 0):
III. Будем считать, что теплообмен между телом и окружающей средой происходит по закону Ньютона: плотность теплового потока ν(P,t), получаемого из внешней среды, пропорциональна разности температуры окружающей среды θ(t) и температуры u внутри V вблизи поверхности S.
Таким образом, мы имеем случай II, где ν(P,t) имеем специфический вид (*), т.е. 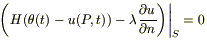
(3в) 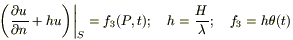
В случае, если температура окружающей среды θ(t) = 0, получим однородное граничное условие 3 го рода: 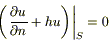
Таким образом, мы приходим к задаче: найти решение уравнения теплопроводности (1), удовлетворяющее нормальным условиям (2) и одному из граничных условий (3). Совершенно аналогично ставятся задачи в одномерном и двумерном случаях. Для уравнения (1) можно также поставить задачу Коши (т.е. задачу без граничных условий)
Замечание: к уравнению (1) приводятся и другие физические задачи: уравнение диффузии, движение вязкой жидкости.
2.1. Метод разделения переменных для конечного стержня
Уравнение теплопроводности относится к уравнениям параболического типа.
Уравнение теплопроводности имеет вид:

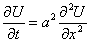

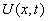
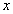
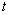

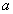
Рассмотрим однородный стержень длины 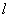
Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия. Для задач этого типа задается только одно начальное условие, а именно, начальная температура в начальный момент времени. Итак,
 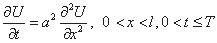 . . | (1) |
 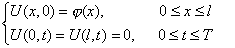 , , | (2) (3) |
где 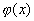
Концы стержня закреплены в термостате. В данном случае тепловая энергя стержня не сохраняется, так как система не является изолированной.
Будем искать решение в виде произведения двух функций

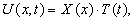
где X(x)- функция только переменного x,

 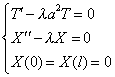 | (4) (5) (6) |
Необходимо определить знак 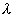
1 случай: Пусть 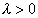
Рассмотрим уравнение (4):

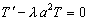
Характеристическое уравнение имеет вид:

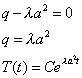
Рассмотрим уравнение (5):

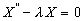
Характеристическое уравнение имеет вид:
 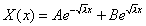 . . | (7) |
Это решение не подходит, так как если 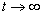
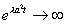
Значит 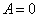
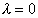
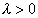
2 случай: Пусть 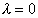
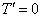
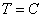
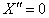
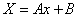
Подставим краевые условия
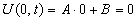
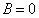
В итоге получим нулевое решение 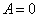
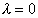
3 случай: Пусть 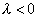
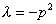

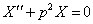
Характеристическое уравнение имеет вид:
Общее решение может быть записано в виде:
 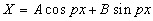 . . | (8) |
Подставим краевые условия.

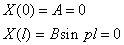
Получаем
 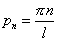 . . | (9) |
Существуют нетривиальные решения уравнения (5), равные
 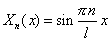 . . | (10) |
Этим значениям 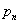

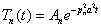
где 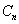
 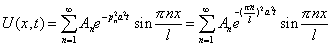 | — общее решение. |
Удовлетворим начальным условиям (2):

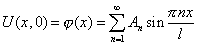
Для выполнения этого начального условия необходимо взять в качестве 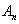

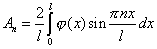
Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.
Уравнение теплопроводности для бесконечного стержня
Рассмотрим задачу с начальными данными на бесконечной прямой. А именно, найдем ограниченную функцию, 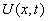
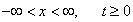
 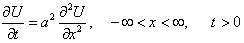 |
и начальному условию
 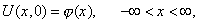 |
где функция 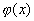
Сделаем преобразование Фурье по переменной 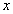

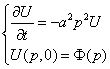

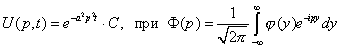

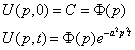
Чтобы получить итоговое решение, нужно провести обратное преобразование Фурье

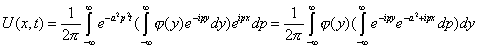

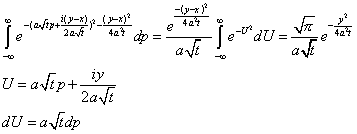
Тогда общее решение имеет вид
 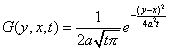 | — функция Грина для уравнения теплопроводности. |
 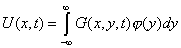 | — общее решение (стандартный вид). |
Эта функция дает решение уравнения теплопроводности с заданным начальным условием.