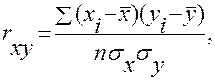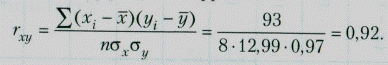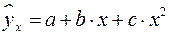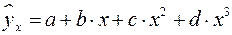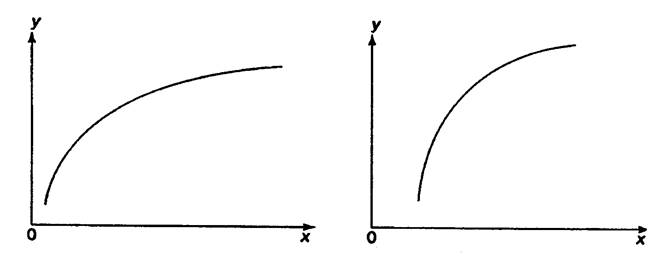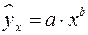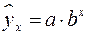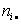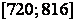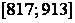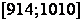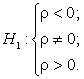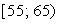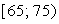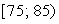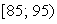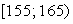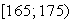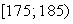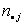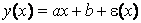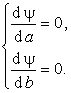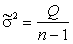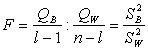Что такое корреляционное поле
Парная корреляция
Парная корреляция позволяет оценить тесноту связи между двумя признаками. Для выявления корреляционной связи между двумя признаками можно построить поле корреляции.
Расположение точек на поле корреляции позволяет судить о наличии и о характере связи (нелинейная, а если линейная, то и о направлении (прямая или обратная)).
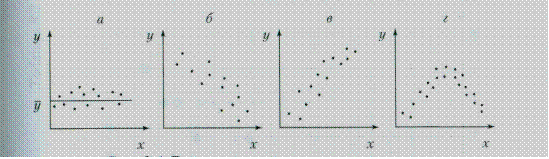
На рис. 1.1 показаны основные возможные способы расположения точек поля корреляции. Если точки поля корреляции располагаются в определенном направлении, то можно предположить наличие связи.
Рис. 1.1. Возможное расположение точек поля корреляции (х; у):
а – корреляция отсутствует; б – корреляция линейная обратная;
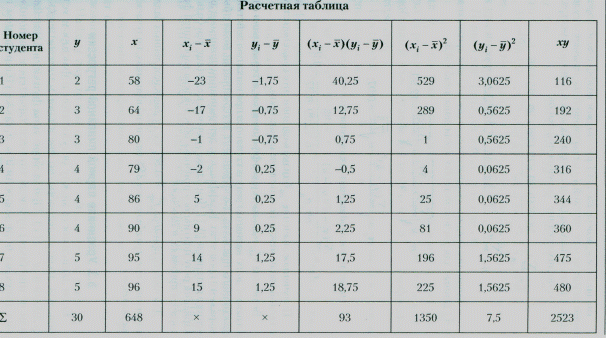
Пример 1.1. Изучается зависимость оценки, полученной на экзамене (у) 8 студентами, от суммы баллов (х), набранных ими в течение семестра. Данные приведены в табл. 1.1.
| Номер студента | Оценка на экзамене (у) | Сумма баллов (х) |
Для построения поля корреляции в координатных осях:
— на оси Х отложим значения баллов х, набранных студентами в течение семестра;
— на оси У покажем значения оценки у, полученной на экзамене студентами;
— нанесем точки с координатами (х; у) для каждого студента.
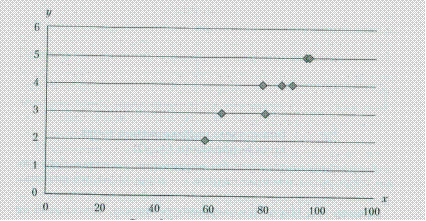
На рис. 1.2 показано поле корреляции. Расположение точек позволяет предположить, что существует прямая линейная связь между оценкой, полученной на экзамене (у) студентами, и суммой баллов (х), полученных ими в течение семестра.
Рис. 1.2. Поле корреляции
Теснота линейной связи измеряется коэффициентом парной корреляции:
где 



Если знаки отклонений от средних совпадают, то связь прямая 
если знаки отклонений не совпадают, то связь обратная 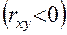

Чем ближе значение 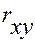
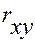
Характеризовать тесноту связи поможет следующая таблица:
| Коэффициент корреляции | Характеристика связи |
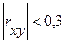 | Слабая |
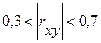 | Средняя |
 | Сильная или тесная |
По данным примера табл. 1.1 рассчитаем коэффициент парной корреляции между оценкой (у), полученной на экзамене студентами, и суммой баллов (х), полученных ими в течение семестра:
— вычислим средние значения признаков:
— вычислим средние квадратические отклонения признаков 

данные для расчета которых приведены в табл. 1.2:
— вычислим коэффициент корреляции:
Полученное значение 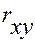
Величина 
Для нашего примера 
Что такое поле корреляции и как оно используется в эконометрике?
Поле корреляции – это поле точек, на котором каждая точка соответствует единице совокупности; ее координаты определяются значениями признаков 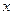
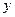
Любое эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующей теории связи между переменными.
В парной регрессии выбор вида математической функции 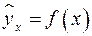
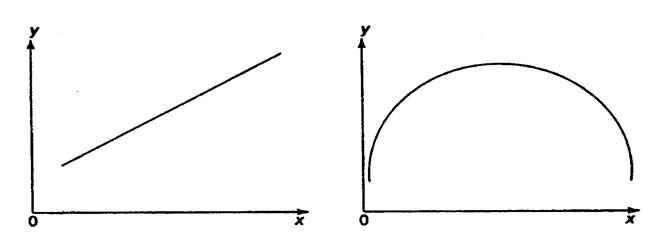
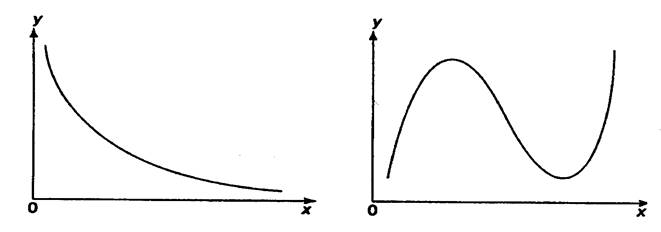
Основные типы кривых, используемые при количественной оценке связей, представлены на рис.
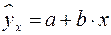
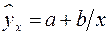
Рис. 1. Основные типы кривых, используемые при
количественной оценке связей между двумя переменными.
Поможем написать любую работу на аналогичную тему
Что такое поле корреляции и как оно используется в эконометрике?
Что такое поле корреляции и как оно используется в эконометрике?
Что такое поле корреляции и как оно используется в эконометрике?
Что такое корреляционное поле
6. Корреляционный анализ и регрессионный анализ данных
6.1. Корреляционный анализ
Корреляционный анализ – это совокупность методов обнаружения так называемой корреляционной зависимости между случайными величинами.
Для двух случайных величин Х и Y корреляционный анализ состоит из следующих этапов:
— построение корреляционного поля и составление корреляционной таблицы;
— вычисление выборочного коэффициента корреляции;
— проверка статической гипотезы о значимости корреляционной связи.
Рассмотрим подробнее каждый из указанных этапов.
Пример 6.1. Исследование зависимости между среднемесячными доходами X на семью (в тыс. у.е.) и расходами Y на покупку кондитерских изделий (в у.е.) представлено в таблице:
Построить корреляционное поле и сделать предварительный вывод о форме зависимости случайных величин.
Решение. Корреляционное поле, построенное по статистическим данным, приведено на рис. 6.1.
При большом объеме выборки результаты группируются и представляются в виде корреляционной таблицы.
Построить корреляционную таблицу и сделать предварительный вывод о форме зависимости случайных величин.
По таблице можно видеть, что в целом для всей совокупности фирм увеличение затрат на рекламу приводит к увеличению количества туристов, пользующихся услугами фирмы. Хотя в отдельных случаях наличие такой зависимости может не усматриваться. Например, сопоставим данные по фирмам с порядковыми номерами 7 и 11. Здесь можно увидеть даже обратное соотношение: у фирмы 11 количество туристов меньше, чем у фирмы 7, хотя затраты на рекламу выше. В каждом отдельном случае количество туристов, воспользовавшихся услугами фирмы, будет зависеть не только от размера затрат фирмы на рекламу, но и от того, как сложатся прочие факторы, определяющие величину результативного признака.
Однако наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, затрудняет восприятие таких параллельных рядов. Особенно это сказывается при большом числе единиц, составляющих изучаемую совокупность. В таких случаях целесообразнее воспользоваться для установления факта наличия связи корреляционной таблицей. Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Поскольку в приводимом примере факторный признак представлен всего пятью вариантами повторяющихся значений, достаточно в первом столбце корреляционной таблицы выписать эти результаты. Для результативного признака необходимо определить величину интервала группировки. Это можно сделать с помощью формулы Стержэсса:
Данная корреляционная таблица уже при общем знакомстве дает возможность выдвинуть предположение о наличии или отсутствии связи, а также выяснить ее направление. Если частоты в корреляционной таблице расположены на диагонали из левого верхнего угла в правый нижний угол (т.е. бóльшим значениям фактора соответствуют бóльшие значения функции), то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали из правого верхнего угла в левый нижний, то предполагают наличие обратной связи между признаками.
Для следующей группы, состоящей из пяти фирм, у которых затраты на рекламу 9 усл. ден. ед.
и т.д. (рассчитанные таким образом средние 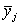
Итак, увеличение средних значений результативного признака с увеличением значений факторного признака еще раз свидетельствует о возможном наличии прямой корреляционной зависимости числа туристов, воспользовавшихся услугами фирмы, от затрат фирмы на рекламу.
Корреляционная таблица позволяет сжато, компактно изложить материал. Поэтому все последующие расчеты можно вести по корреляционной таблице.
Выборочный коэффициент корреляции Пирсона для группированной 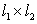
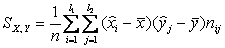
– выборочная ковариация; 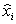
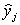
– соответствующие выборочные дисперсии.
Для выборочной ковариации 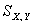
являющаяся аналогом формулы 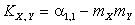
При этом, чем ближе 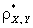
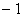
подкреплена проверкой гипотезы. Проверка гипотезы о наличии корреляции осуществляется следующим образом. Основная гипотеза – отсутствие линейной статистической связи ( 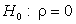
где обозначено 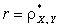
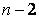
Пример 6.3. В таблице представлены результаты измерений роста Х (см) и веса Y (кг) 50 мужчин – слушателей военной академии:
Вычислить выборочный коэффициент корреляции и проверить гипотезу о значимости корреляционной связи.

выборочные вторые начальные моменты
Далее, используя формулы (6.2) – (6.4), получаем:
Наконец, по формуле (6.1) определяем:
Замечание. Несколько обескураживающий результат предыдущего примера( 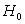
Фишером было доказано, что при 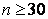
и математическим ожиданием
Стандартизуя V, получим подходящую статистику Фишера:
центрирование статистики V в формуле (6.8) осуществляется на эту величину.
Таким образом, при 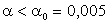
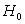
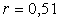
6.2. Регрессионный анализ
Зависимость между случайными величинами X и Y называется стохастической, если с изменением одной их них (например, Х) меняется закон распределения другой ( Y). В качестве примеров такой зависимости приведем зависимость веса человека ( Y) от его роста ( Х), предела прочности стали ( Y) от ее твердости ( Х) и т.д.
В теории вероятностей стохастическую зависимость Y от Х описывают условным математическим ожиданием:
Если 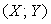
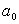
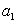
уравнением регрессии в этом случае является прямая линия
В реальных экспериментах, связанных со статической обработкой опытных данных, условный закон распределения случайной величины Y при условии 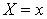
Во многих случаях можно считать, что «независимая» переменная Х находится под контролем экспериментатора, и может бать измерена с любой заданной точностью, в то время как измеряемые значения Y как функции от Х (выборочные значения 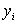
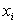
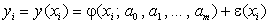
где 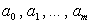
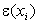
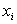
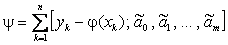
Указанный критерий минимизации суммы квадратов отклонений носит название метода наименьших квадратов (сокращенно МНК), а полученные в результате решения этой задачи оценки 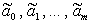

Из этого выражения следует, что
что и требовалось доказать.
Замечание. На практике ошибки измерений часто удовлетворяют поставленным в теореме условиям в силу центральной предельной теоремы.
Регрессионный анализ проводится в три этапа.
На третьем этапе анализируют качество построения модели: проверяются так называемые корректность и адекватность модели. Этот этап осуществляется средствами проверки статистических гипотез.
Искомые оценки являются решениями следующей задачи минимизации:
Получаем следующую систему линейных алгебраических уравнений для неизвестных значений а и b:
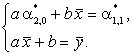
Решение системы (2), как нетрудно убедиться, имеет вид:
где 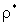
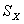
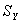
Уравнение линейной регрессии приобретает вид:
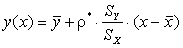
Заметим, что полученное уравнение аналогично теоретическому уравнению регрессии, если заметить все входящие в него вероятностные моменты соответствующими выборочными оценками в соответствии с методом подстановки.
6.3 Однофакторный дисперсионный анализ
Формулируется следующая линейная модель дисперсионного анализа:
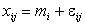
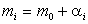
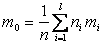
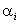
Напомним, что для проверки этой гипотезы использовалась статистика Стъюдента W, основанная на нормированной разности выборочных средних. Фишером доказано, что при 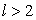
Обозначим выборочное среднее i-ой выборки:
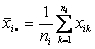
общее среднее объединенной выборки:
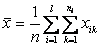
объем объединенной выборки:
т.е. тотальное среднее равно среднему арифметическому внутригрупповых средних.
Обозначим через сумму квадратов отклонений результатов наблюдений от общего среднего
Если гипотеза 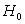
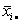
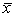
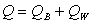
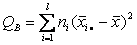
– сумма квадратов отклонений «внутри групп»,
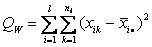
– сумма квадратов отклонений « внутри групп».
Покажем, как получается это разбиение. Преобразуем разность:
Возведем в квадрат:
Далее обе части равенства необходимо просуммировать сначала по k от 1 до 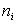
Выражение для этих сумм можно преобразовать к виду более удобному для вычислений:
Из этой теоремы и теоремы Фишера следует, что статистика
Пример 1. Три группы водителей обучались по различным методикам. По окончанию срока обучения был произведен тестовый контроль над случайно отобранными водителями из каждой группы. Результаты контроля сведены в следующую таблицу: