Что такое конспект по физике

Конспект: что это такое и как его писать

Обычно студенты еще в школе приобретают навыки составления конспекта. У тех же, кто в старших классах не выработал ценного умения быстро и систематизированно делать письменные заметки по существу, в первые месяцы учебы в вузе возникают проблемы: три-четыре полуторачасовые лекции в день или работа с источниками при подготовке к семинару превращаются в затяжную пытку. Оказывается, не всегда нужно записывать все, что говорит лектор, или копировать в тетрадь огромные фрагменты учебных материалов: правильно писать конспект – настоящее искусство, которому при желании можно быстро научиться.

Что такое конспект

Конспект– это краткая письменная фиксация основных фактических данных, идей, понятий и определений, устно излагаемых преподавателем или представленных в литературном источнике. Причем такой вид аналитической обработки материала должен отражать логическую связь частей прослушанной или прочитанной информации.

Результат конспектирования – хорошо структурированная запись, позволяющая ее автору с течением времени без труда и в полном объеме восстановить в памяти нужные сведения, а любому другому читателю – получить целостное представление о кратко изложенной теме.

Замена конспектирования стенографированием или переносом в тетрадку огромных фрагментов из учебников и научных статей непродуктивна и опасна:

Вести конспекты в вузах не учат, но разобраться в этой науке можно и самостоятельно, ознакомившись с основными типами краткого изложения содержания первоисточников, чтобы выбрать разновидность, наиболее подходящую для конкретных обстоятельств.

Для разных целей и дисциплин подходят различные виды конспектов. Они отличаются структурой, объемом, техникой составления.

План-конспект

За основу берется план, который нередко предлагается лектором в начале занятия или самостоятельно составляется перед прочтением книги. По мере раскрытия вопросов каждый подпункт «обрастает» комментариями, и в итоге они превращаются в структурированный, логический текст. Такой конспект отлично подойдет для подготовки к выступлениям на семинарах, позволит не упустить важные моменты и раскрыть суть поставленного вопроса.

Схематический план

Обычно используется для проработки текста, реже, чтобы кратко записать лекцию, если заранее известно ее содержание и преподаватель практически диктует. С его помощью удобно структурировать информацию и устанавливать взаимосвязь между основными моментами изучаемого материала, что способствует его лучшему усвоению. Составляется план-схема в виде списка вопросов, на которые в ходе прочтения книги или прослушивания лекции даются ответы.

Текстуальный конспект

Составить такой конспект непросто, зато в результате получается реферативная запись, насыщенная тезисами и выдержками из первоисточника, целостно и развернуто отражающими его суть. Обычно он делается на основе плана, иногда вопросного, который дополняется точными фрагментами из текста. Такой конспект актуален для гуманитариев, например, изучающих литературу или философию, где авторские цитаты имеют большое значение.

Свободный

Может сочетать в себе все перечисленные выше варианты и состоять из выписок, цитат, плана, тезисов и прочего. Свободное конспектирование позволяет изложить материал максимально целостно и подходит для различных дисциплин.

Тематический конспект

Суть этого способа ведения записей в том, чтобы осветить изучаемый вопрос с различных точек зрения, используя не один, а несколько источников. Такой конспект максимально полно раскрывает тематику, однако больше подходит для самостоятельной работы с печатным текстом.

Графический

Чаще всего используется студентами, изучающими технические науки. В его основе – схематичные рисунки, графики, таблицы, которые лектор часто дает в мультимедийной презентации или просто на плакатах, развешенных на доске. Достаточно перенести их в тетрадь и сделать краткие пояснения к ним.

Как писать

Хороший конспект сделать непросто, но никто и не обещал, что в вузе будет легко. Чтобы понять, правильно ли составлены записи, следует перечитать их через пару дней. Если без труда удалось восстановить в памяти важную информацию, значит, все в порядке. Если нет, придется потренироваться или сменить тактику, чтобы окончательно определиться, как делать конспект так, чтобы он был хорошим подспорьем в подготовке к занятиям и экзаменам, а через пару лет при необходимости смог послужить справочником.

Конспект лекций

Правила написания конспекта лекции весьма условны, но чтобы сделать его максимально полным и понятным, надо:

Литературы

Прежде чем приступить к составлению конспекта литературного источника, стоит хотя бы один раз внимательно полностью прочитать текст. Это позволит выявить основные особенности материала, стиль и характер изложения, главную идею, разобраться с незнакомыми терминами.

Дальнейшая работа связана с анализом информации. На этом этапе следует отделить главное от второстепенного, структурировать материал, располагая его в логически правильном порядке.

Оформление конспекта

Поскольку конспектирование в большинстве случаев дело добровольное и преподавателями не контролируемое, претензий к внешнему виду записей никто предъявлять не будет. Но, чтобы успевать за ходом мысли (и скоростью речи) лектора или не убивать кучу времени на составление заметок о прочитанном и при этом в результате получить максимально информативный и полезный конспект, надо придерживаться простых правил:

Так проблем с расшифровкой конспекта не возникнет даже спустя некоторое время.

Следование этим простым правилам оформления конспектов по не только существенно упростит работу на лекциях, но и подготовку к зачетам и экзаменам.

Необычные виды конспектирования

Если стандартные способы ведения записей не позволяют получить информативные и полезные конспекты, можно прибегнуть к необычным техникам.

Майнд-карты

Mind-mapping – популярная техника конспектирования, которая придется по вкусу любителям мозговых штурмов. В кружочке или рамке в центре страницы указывается тема лекции. В течение занятия к этой отправной точке присоединяются дополнительные блоки, которые отводятся под логически связанные с основным понятием ключевые слова и идеи. Для большей информативности текст можно дополнять рисунками и значками.

Для создания ментальных карт лучше использовать листы большого формата (не менее А4). Записи располагаются от центра к периферии.

Метод Корнелла

Этот метод пользуется большой популярностью у американских преподавателей и студентов. Конспект, составленный в такой технике, стимулирует к перечитке записей, их дополнению и переработке. Перед тем как начинать делать заметки, надо разделить страницу на две неравные колонки (левая меньше, правая больше) и оставить немного места вверху и внизу листа для заголовка, даты и подведения итогов.

Во время лекции записи делаются привычным образом, основная информация располагается в правой колонке. В левой уже после занятия помещаются наиболее значимые идеи, даты и понятия. В 24 часов необходимо окончательно оформить конспект, заполнив нижнее поле. Для этого надо несколькими предложениями сформулировать основную идею записей.

Если в течение суток не подвести итоги записанного, техника Корнелла лишена смысла и не принесет дополнительной пользы в сравнении с обычным конспектом.

Пример конспекта

Правильно составленные конспекты нередко передаются из рук в руки, так как понятны даже тем, кто впервые слышит о теме записей. Приблизительно так может выглядеть краткая запись, сделанная с использованием общепринятых сокращений, знаков и выделений:

ТЕМПЕРАТУРОЗАВИСИМЫЕ ИЗМЕНЕНИЯ В ЛИПИДНОЙ И ВОДНОЙ ФАЗЕ

Глубокое охлаждение может стать причиной серьезных нарушений в биосистемах в результате:

Фазовые превращения липидов – переход их ансамблей из жидко- в твердокристаллическое состояние и наоборот. Для криобиологии важны структурные изменения воды и их учет в жидкой фазе, с которой контактирует биообъект.

!Общее для фаз. переходов в липидах и водных р-рах – оба относятся к фаз. превращениям 1-го рода.

Фаза – гомогенная термодинамическая сис-ма, в кот. отсутствуют поверхности раздела, отделяющие друг от друга макроскопические части, отличающиеся по своим свойствам и составу.

Фаз. переход 1-го рода – превращение, при котором потенциал Гиббса сис-мы – const, а внутренняя энергия и плотность (или энтальпия и энтропия) претерпевают скачкообразные изменения => фаз. переход 1-го рода – кооперативное упорядочение сис-мы или ее части, связанное с выделением или поглощением тепла.

В общем, было бы желание, а освоить правила написания конспекта несложно. Составление кратких записей отлично развивает ассоциативную память, а умение хорошо структурировать информацию пригодится в жизни не меньше полного курса по сопромату.

Источник

Что такое конспект по физике

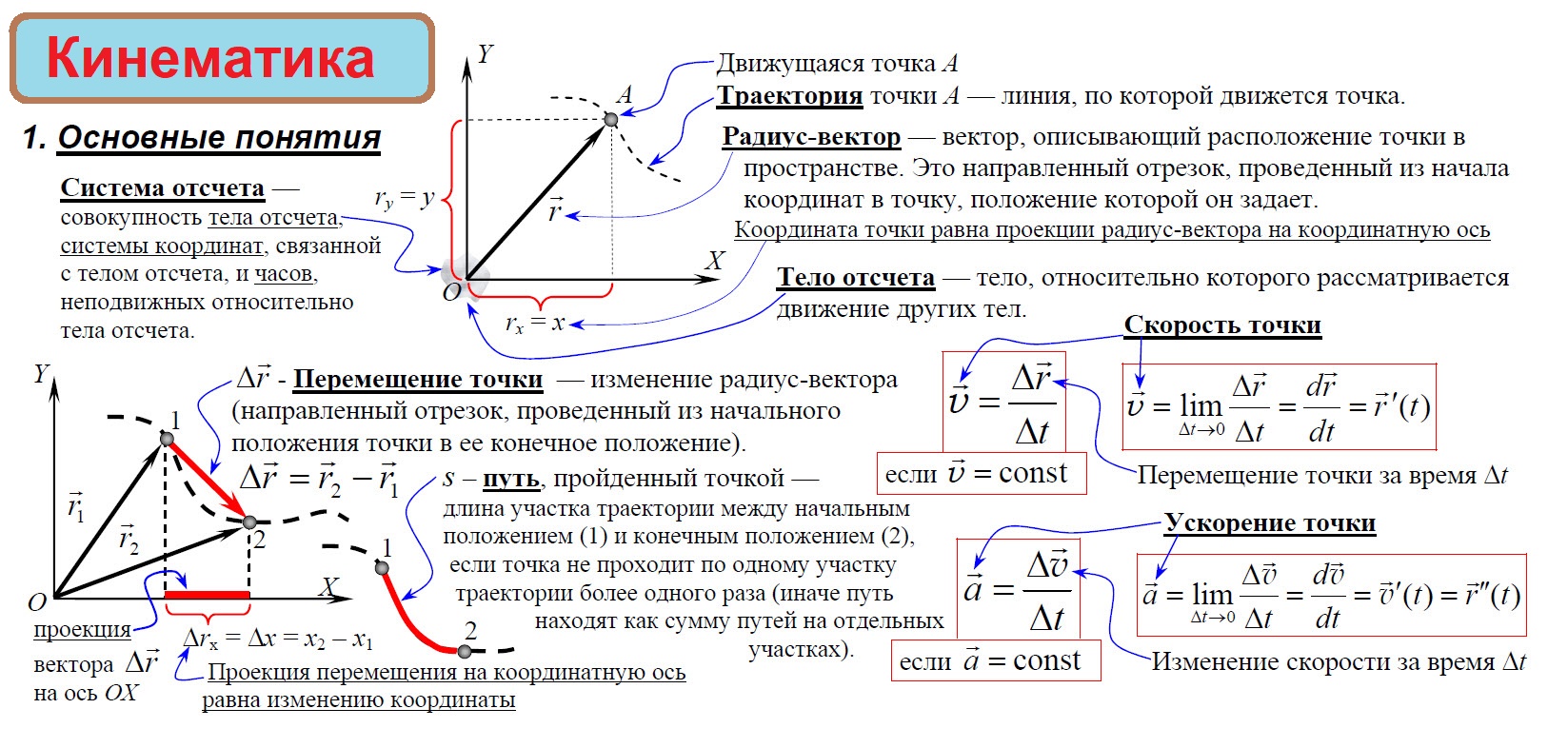
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.

Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.

Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.

Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).

Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.

Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.

Типы движений

1. Равномерное движение

1.1. Равномерное прямолинейное движение

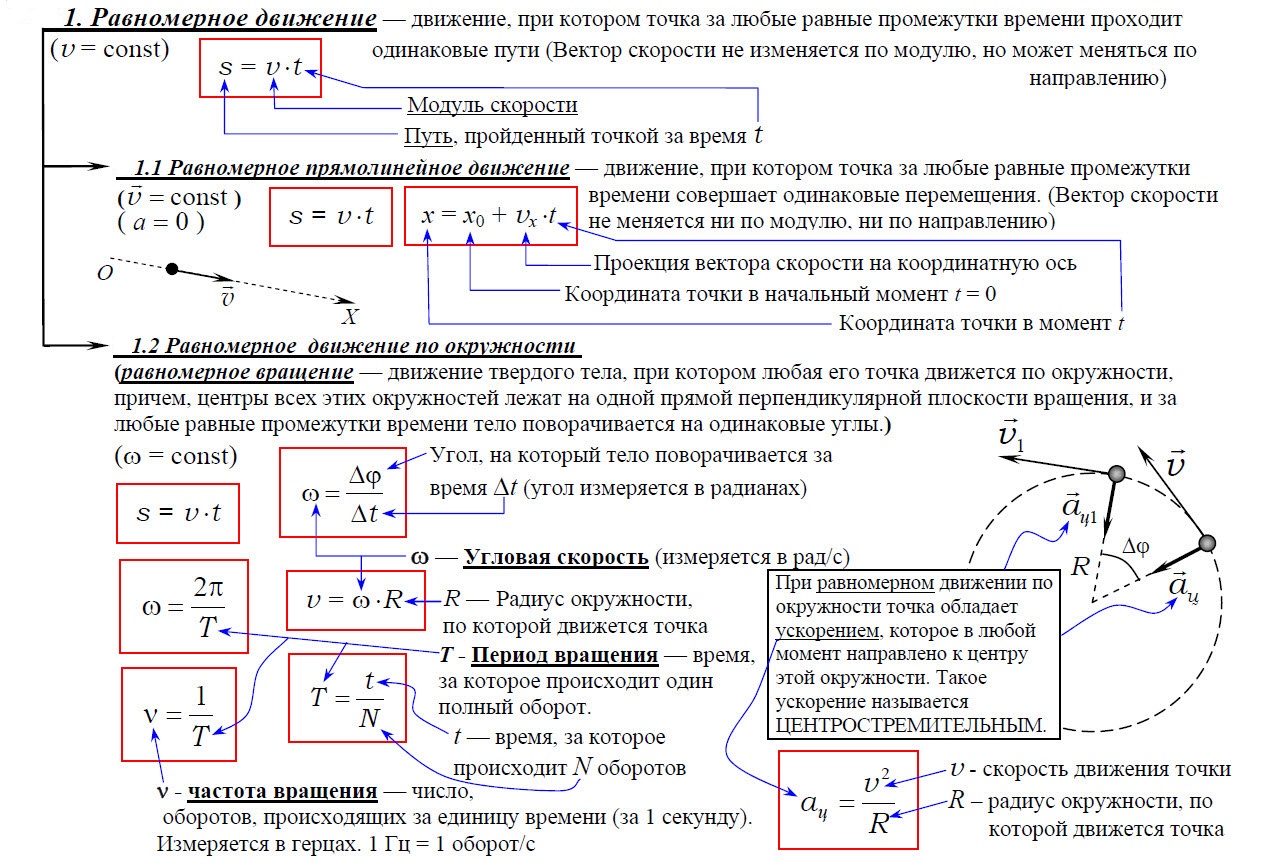
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.

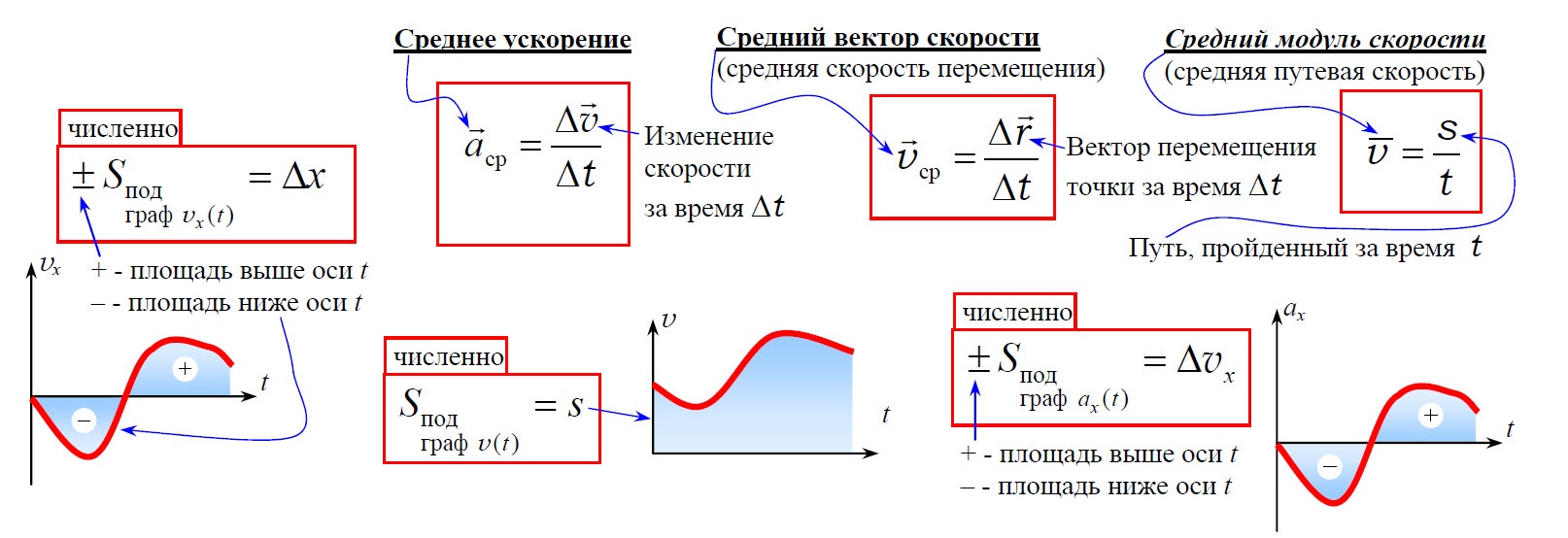
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.

Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.

Уравнение равно-прямолинейного движения x = x o + υ ox t показывает, что координата линейно зависит от времени.

Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.

1.2 Равномерное движение по окружности (равномерное вращение)

Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.

Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

2. Движение с постоянным ускорением

Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.

Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.

Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.

Уравнение равноускоренного движения y = yo + υoyt + ½ay t² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ay t показывает, что скорость линейно зависит от времени.

Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.

Источник

Вводный урок на тему «Что изучает физика»

Описание разработки

Цели урока:

1. Познакомить учащихся с новым предметом школьного курса. Определить место физики, как науки.

2. Научить различать физические явления и тела.

3. Познакомить с методами изучения физики.

1. Показать значение познания мира через мышление.

2. Формировать моральные, волевые и эстетические качества личности.

1. Развивать внимание и любознательность.

2. Развивать представление о применении человеком физических знаний в быту и технике.

Структура урока:

1. Организационный этап.

2. Мотивационный этап.

3. Изучение нового материала.

4. Закрепление изученного.

5. Домашнее задание.

Ход урока.

1. Организационный этап.

Взаимное приветствие учащихся и учителя.

Прежде, чем отправиться в увлекательное путешествие в мир физики, давайте определимся с учебниками и тетрадями:

1) рабочая тетрадь по физике;

2) 2 тонкие тетради: для лабораторных работ по физике;

Для контрольных работ по физике.

3. Сборник задач по физике Лукашик В. И., Иванова Е. В. 7- 9 классы.

2. Мотивационный этап.

Итак, начнём наше путешествие в мир физики с вопроса «Что изучает физика?»

Пишем сегодняшнее число и тему урока.

Что изучает физика? – спросите вы. Я отвечу: «Физика – это всё, что нас окружает. »

Обернитесь вокруг: вы видите парты, столы, стулья, шкафы, окна, за окном синее небо, летают птицы, дует ветер… Это всё физика.

В течение всей своей жизни, начиная с самого начала, мы с вами постоянно познаём окружающий нас мир начиная с младенческого возраста, мы усваиваем огромное количество информации об окружающем мире, на что редко обращаем внимание. С детства мы с вами знаем что такое «горячо», что такое «холодно», что такое «мягкое» и что такое «жёсткое» или «твердое».

Мы с Вами знаем, что чистое небо – синее, трава – зелёная, клубника – красная и т. д. иными словами мы знаем много характеристик окружающего нас пространства, или окружающей нас природы.

Ведь земля, вода, воздух, растения, животные, люди, и все предметы вокруг нас – это всё природа. И именно природу, её законы и изучает физика.

3. Изучение нового материала.

3.1. Из истории возникновения физики.

Физика является одной из древнейших наук. Древний человек наблюдал за окружающим миром, от которого зависела вся его жизнь, пытался понять явления природы. Солнце давало людям тепло и приносило засухи. Дожди поливали живительной влагой и вызывали наводнения; бедствия несли ураганы и землетрясения.

Древние люди не знали причин их возникновения и приписывали разрушительные явления сверхъестественным силам. Постепенно люди начали понимать действительные причины природных явлений и их взаимосвязь. Так начали зарождаться науки о природе, одной из которых была физика.

В 4 веке д.н.э. древнегреческий учёный Аристотель ввёл понятие «физика». Слово «физика»в переводе с греческого означает «природа».

В русском языке это слово появилось в 18 веке, благодаря Михаилу Васильевичу Ломоносову.

3.2. Взаимосвязь физики с другими науками

Но не только физика является наукой, изучающей природу. География, биология, астрономия также изучают природу, но они не дают какого – либо полного представления о структуре окружающего нас мира.

Так, география изучает климат, а физика объясняет причину возникновения именно таких климатических условий, зарождение циклонов и т.д.

Биология изучает растения и животный мир, физика объясняет, к примеру, почему не болит голова у дятла, благодаря чему мы слышим…

Астрономия изучает звёзды, Солнце, планеты, а физика объясняет, почему планеты движутся вокруг Солнца, а не улетают от него и т.д.

Таким образом, физика даёт полное представление о структуре окружающего мира. Физика позволяет познать силы природы и поставить их на службу человеку, позволяет понять современную технику и развивать её дальше.

Ведь не очень давно люди ездили на тарантасах, запряжённых лошадьми, жали рожь и пшеницу серпами, сидели при свете горящих лучин и только в сказках мечтали о различных волшебствах… И это волшебство случилось… и во сём этом мы должны быть благодарны физике.

Итак, что же такое физика? Запишем определение.

Физика – наука о природе и о физических явлениях, которые в ней происходят.

А физические явления – это изменения, происходящие в природе.

Источник

Физика в конспектах

Фи́зика (от греч. φύσις — природа) — область естествознания, наука, изучающая наиболее общие и фундаментальные закономерности, определяющие структуру и эволюцию материального мира.

Содержание

Предмет физики [ править ]

Физика — это наука о природе в самом общем смысле. Она изучает вещество (материю) и энергию, а также фундаментальные взаимодействия природы, управляющие движением материи.

Некоторые свойства являются общими для всех материальных систем, например, сохранение энергии — такие свойства называют физическими законами. Физику иногда называют «фундаментальной наукой», поскольку другие естественные науки (биология, геология, химия и др.) описывают только некоторый класс материальных систем, подчиняющихся законам физики. Например, химия изучает молекулы и образованные из них химические вещества. Химические же свойства вещества однозначно определяются физическими свойствами атомов и молекул, которых описываются в таких разделах физики, как термодинамика, электромагнетизм и квантовая физика.

Физика тесно связана с математикой — математика предоставляет аппарат, с помощью которого физические законы могут быть точно сформулированы. Физические теории почти всегда формулируются в виде математических выражений, причём используются более сложные разделы математики, чем обычно в других науках. И наоборот, развитие многих областей математики стимулировалось потребностями физических теорий (см. математическая физика).

Механика [ править ]

Меха́ника (из греческого μηχανική, от μηχανή — «машина, прибор») — это раздел физики, изучающий механическое движение, то есть движение тел в пространстве и времени. Механика Ньютона изучает не слишком быстрое движение макроскопических тел, то есть скорости много меньше скорости света и тел, больших размера атома.

Векторы [ править ]

Вектор — это математический объект, характеризующийся величиной, направлением и складывающийся по правилу параллелограмма. Вектор можно переносить параллельно себе в любую точку пространства.

Операции над векторами [ править ]

Сложение векторов [ править ]

Сложение двух векторов происходит по правилу параллелограмма (треугольника). Пусть вектор a → = A B → <\displaystyle <\vec >=<\vec >> и b → = B C → <\displaystyle <\vec >=<\vec >> . Тогда c → = A C → <\displaystyle <\vec >=<\vec >> называют суммой векторов:

Умножение вектора на число [ править ]

Скалярное произведение [ править ]

то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат, то есть

a → b → = x 1 x 2 + y 1 y 2 + z 1 z 2 <\displaystyle <\vec ><\vec >=x_<1>x_<2>+y_<1>y_<2>+z_<1>z_<2>>

Векторное произведение [ править ]

Векторным произведением двух ненулевых векторов a → <\displaystyle <\vec >> и b → <\displaystyle <\vec >> называется вектор c → <\displaystyle <\vec >> , такой что модуль этого вектора равен произведению модулей векторов на синус угла между ними:

Направление вектора выбирается или по правилу правого винта или через правую тройку векторов.

Правило правого винта [ править ]

Правая тройка векторов [ править ]

Три вектора называются упорядоченной тройкой (правой или левой), если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим. Тройка некомпланарных векторов a → b → c → <\displaystyle <\vec ><\vec ><\vec >> называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.

Если известны координаты векторов в ортогональной системе координат, то векторное произведение можно найти из определителя третьего порядка.

Определитель [ править ]

Если два вектора a → <\displaystyle <\vec >> и b → <\displaystyle <\vec >> определены своими прямоугольными координатами:

то их векторное произведение имеет вид

Для запоминания этой формулы удобно использовать символ определителя :

[ a → b → ] = | i → j → k → x 1 y 1 z 1 x 2 y 2 z 2 | <\displaystyle [<\vec ><\vec >]=<\begin<\vec >&<\vec >&<\vec >\\x_<1>&y_<1>&z_<1>\\x_<2>&y_<2>&z_<2>\end>>

Кинематика [ править ]

Кинема́тика (от греч. κινέω «двигаю») — это раздел механики, изучающий механическое движение без анализа причин его вызывающих.

Основная задача кинематики: получение зависимости от времени координат (радиус-векторов) r → ( t ) <\displaystyle <\vec >(t)> всех материальных точек исходя из того, что определены их начальные условия и ускорения в любой момент времени a → ( t ) <\displaystyle <\vec >(t)> .

Механи́ческое движе́ние — простейшая форма движения тел, заключающаяся в изменении с течением времени положения одних тел относительно других, либо положения частей тела друг относительно друга. При этом тела взаимодействуют по законам механики.

Основные понятия [ править ]

Радиус-вектор и его производные [ править ]

Ускорение, или скорость изменения скорости, это:

Вектор ускорения может меняться за счет изменения его направления, величины, или и того и другого. Если скорость уменьшается, иногда пользуются термином «замедление», но вообще, термин «ускорение» относится к любому изменению скорости.

Нам понадобятся еще несколько определений:

Скорость [ править ]

Мгновенная скорость — первая производная от радиуса-вектора по времени, она всегда направлена по касательной к траектории движения тела в данной точке.

Скорость в координатном представлении:

V → = V x ⋅ i → + V y ⋅ j → + V z ⋅ k → <\displaystyle <\vec >=V_\cdot <\vec >+V_\cdot <\vec >+V_\cdot <\vec >> | V → | = V x 2 + V y 2 + V z 2 <\displaystyle |<\vec >|=<\sqrt ^<2>+V_^<2>+V_^<2>>>>

Ускорение [ править ]

Мгновенное ускорение — это вторая производная от радиуса-вектора по времени.

Ускорение в координатном представлении:

a → = a x ⋅ i → + a y ⋅ j → + a z ⋅ k → <\displaystyle <\vec >=a_\cdot <\vec >+a_\cdot <\vec >+a_\cdot <\vec >> | a → | = a x 2 + a y 2 + a z 2 <\displaystyle |<\vec >|=<\sqrt ^<2>+a_^<2>+a_^<2>>>>

Преобразования Галилея [ править ]

Преобразования Галилея — в классической механике (механике Ньютона)это преобразования координат и времени при переходе от одной системы отсчета к другой.

\;=\; \;+\; >»> r → = r → o − r ′ → ( r → − Δ r → ) = ( r → o + Δ r → o ) − ( r ′ → + Δ r ′ → ) r → Δ t = r → o Δ t + r ′ → Δ t ⟩ ⇒ V → > = V → o > + V ′ → > <\displaystyle <\begin<\vec >=<\vec >_—<\vec >\;\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\(<\vec >-\Delta <\vec >)=(<\vec >_+\Delta <\vec >_)-(<\vec >+\Delta <\vec >)\\<\frac <\vec ><\Delta>>=<\frac <<\vec >_><\Delta>>+<\frac <\vec ><\Delta>>\;\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \end><\Bigg \rangle >\quad \Rightarrow \quad \;=\; \;+\; > \;=\; \;+\; >»/>

+ =<\vec >_+<\vec >>»> V → = lim Δ t → 0 V → o > + V ′ → >= V → o + V ′ → <\displaystyle <\vec >\;=\lim _<\Delta t\rightarrow 0>\; + =<\vec >_+<\vec >> + =<\vec >_+<\vec >>»/>

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую:

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, те a o = o <\displaystyle \ a_=o> то ускорение a → <\displaystyle <\vec >> тела относительно обеих систем отсчета одинаково, — принцип относительности Галилея.

Прямолинейное, равноускоренное и равномерное движение [ править ]

Пусть движение некоторого тела описывается функцией радиус-вектора от времени, меняющейся по следующему закону:

r → ( t ) = A → + B → t + C → t 2 2 <\displaystyle <\vec >(t)=<\vec >+<\vec >t+<\vec >\;\over 2>>

r → ( t + Δ t ) = A → + B → ( t + Δ t ) + C → ( t + Δ t ) 2 2 <\displaystyle <\vec >(t+\Delta)=<\vec >+<\vec >(t+\Delta)+<\vec >\;<(t+\Delta)^ <2>\over 2>>

r → ( t + Δ t ) − r → ( t ) = B → Δ t + C → 1 2 ( Δ t ) ( 2 t + Δ t ) <\displaystyle <\vec >(t+\Delta)-<\vec >(t)=<\vec >\Delta+<\vec >\;<1 \over 2>(\Delta)(2t+\Delta)>

>»> Δ r → Δ t = B → + C → t + C → 2 Δ t = V → > <\displaystyle <\frac <\Delta <\vec >><\Delta>>=<\vec >+<\vec >\;t+<<\vec > \over 2>\Delta= > >»/>

=<\vec >+<\vec >t>»> V → = lim Δ t → 0 V → >= B → + C → t <\displaystyle <\vec >=\lim _<\Delta\rightarrow <0>> =<\vec >+<\vec >t> =<\vec >+<\vec >t>»/>

V → ( t + Δ t ) = B → + C → ( t + Δ t ) <\displaystyle <\vec >(t+\Delta)=<\vec >+<\vec >(t+\Delta)>

=<\vec >>»> V → Δ t = C → Δ t a → = lim Δ t → 0 a → >= C → <\displaystyle <\vec >\Delta=<\vec >\Delta\quad \quad \quad <\vec >=\lim _<\Delta\rightarrow <0>> =<\vec >> =<\vec >>»/>

Таким образом, рассмотренная зависимость радиус-вектора соответствует механическому движению с постоянным ускорением, при котором скорость тела за любые равные промежутки времени получают равные приращения. Такое движение называется равноускоренным и описывается в общем виде следующей системой уравнений.

r → = r → o + V → o + 1 2 a → t 2 V → = V o + a → t a → = c o n s t ⟩ <\displaystyle <\begin<\vec >=<\vec >_+<\vec >_+<\frac <1><2>><\vec >t^<2>\quad \\<\vec >=V_+<\vec >t\;\quad \quad \quad \\<\vec >=const\;\quad \quad \quad \quad \end><\Bigg \rangle >>

Криволинейное движение [ править ]

V → ( t ) = | V → ( t ) | ⋅ τ → ( t ) = V ( t ) ⋅ τ → ( t ) <\displaystyle <\vec >(t)=|<\vec >(t)|\cdot <\vec <\tau >>(t)=V(t)\cdot <\vec <\tau >>(t)>

V → ( t + Δ t ) = V → + Δ V → = ( V + Δ V ) ⋅ ( τ → + Δ τ → ) <\displaystyle <\vec >(t+\Delta t)=<\vec >+\Delta <\vec >=(V+\Delta V)\cdot (<\vec <\tau >>+\Delta <\vec <\tau >>)>

Нормальное ускорение [ править ]

Теперь давайте найдем формулу для нормального ускорения, то есть ускорения при движении по кругу.

Динамика [ править ]

Дина́мика (от греч. δύναμις «сила») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.

Ма́сса — скалярная физическая величина, являющаяся количественной мерой инертности тела, а также характеризующая количество вещества, Си́ла — векторная физическая величина, являющаяся мерой взаимодействия тел и приводящая к появлению у тела ускорения или к деформации тела. Сила характеризуется величиной, направлением и точкой приложения, Линия действия силы — это линия, вдоль которой действуют силы. Если тело является абсолютно твердым, то точку приложения силы можно перемещать вдоль линии действия силы в пределах тела. Импульс — векторная физическая величина, равная произведению массы тела на его скорость: p → = m v → <\displaystyle <\vec

>=m<\vec >> , Энергия — характеристика движения и взаимодействия тел, их способность совершать изменения во внешнем мире. Часто можно встретить упрощённое определение энергии как способности тела совершать работу. Будучи удобным в классической механике, такое определение, тем не менее, не вполне точно, так как не всегда всю энергию можно перевести в механическую работу (см. второе начало термодинамики),

Масса [ править ]

Под массой в динамике понимают два различных свойства вещества:

Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому коэффициент пропорциональности обычно выбирают равным единице и говорят о равенстве инертной и гравитационной масс. Равенство инертной и гравитационной масс составляет содержание слабого принципа эквивалентности — составной части Эйнштейновского принципа эквивалентности, который является одним из основных положений общей теории относительности.

Масса обладает следующими свойствами:

Энергия [ править ]

Энергия в физике встречается в разных видах:

Законы Ньютона [ править ]

Первый закон Ньютона гласит, что замкнутая система продолжает оставаться в состоянии покоя или прямолинейного равномерного движения. По сути, этот закон постулирует инертность тел. Это может казаться очевидным сейчас, но это не было очевидно на заре исследований природы. Так, например, Аристотель утверждал, что причиной всякого движения является сила, то есть у него не было движения по инерции.

Второй закон Ньютона диктует, на что на самом деле влияет сила: сила, действующая на систему извне, приводит к ускорению системы. Заметим, что если система замкнута, то на неё не действует никаких сил, следовательно, по второму закону Ньютона, её ускорение нуль, а значит, она может двигаться только с постоянной скоростью. Таким образом, первый закон Ньютона является частным случаем второго.

Третий закон Ньютона объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F → 12 <\displaystyle <\vec >_<12>> , а второе — на первое с силой F → 21 <\displaystyle <\vec >_<21>> . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным системам, а потому вовсе не компенсируются.

Следствия [ править ]

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, оказывается, что многие силы вокруг нас (в частности, поле сил гравитации) обладают свойством потенциальности: работа внешних сил по переносу тела из одной точки в другую не зависит от конкретного пути (на языке математики: ротор силового поля тождественно равен нулю). В этом случае силу (векторную величину) можно представить как градиент некоторой скалярной величины — потенциала. Для того, чтобы третий закон Ньютона автоматически выполнялся, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U(|r₁-r₂|). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:

Силы инерции [ править ]

Законы Ньютона, строго говоря, справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона. Однако часто, для упрощения рассмотрения, вводят некую фиктивную «силу инерции», и тогда эти уравнения движения переписываются в виде, очень похожем на второй закон Ньютона. Математически здесь все корректно, но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального взаимодействия. Ещё раз подчеркнем: «сила инерции» — это лишь удобная параметризация того, как отличаются законы движения в инерциальной и неинерциальной системах отсчета.

Комментарии ко второму закону Ньютона [ править ]

Уравнение F = ma (то есть второй закон Ньютона) является дифференциальным уравнением второго порядка, поскольку ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости. Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления как инерция, колебания, волны.

Специальная теория относительности [ править ]

Специа́льная тео́рия относи́тельности (СТО), ча́стная тео́рия относи́тельности — теория, заменившая механику Ньютона при описании движения тел со скоростями, близкими к скорости света. При малых скоростях различия между результатами СТО и ньютоновской механикой становятся несущественными.

Создание СТО [ править ]

Специальная теория относительности была разработана в начале XX века усилиями Г. А. Лоренца, А. Пуанкаре и А. Эйнштейна. Вопрос приоритета в создании СТО имеет дискуссионный характер: основные положения и полный математический аппарат теории, включая групповые свойства преобразований Лоренца, в абстрактной форме были впервые сформулированы А. Пуанкаре в работе «О динамике электрона» на основе предшествующих результатов Г. А. Лоренца, а явный абстрактный вывод базиса теории — преобразований Лоренца, из минимума исходных постулатов был дан А. Эйнштейном в практически одновременной работе «К электродинамике движущихся сред». По этому поводу в англоязычной Википедии есть отдельная статья.

Постулаты Эйнштейна [ править ]

СТО полностью выводится на физическом уровне строгости из двух постулатов (предположений):

Формулировка второго постулата может быть шире: «Скорость света постоянна во всех инерциальных системах отсчёта», но для вывода СТО достаточно его исходной формулировки Эйнштейном, записанной выше. Приписывание постулатов Эйнштейну правомерно в той степени, что до его работы эти уже сформулированные отдельно друг от друга (в частности, А. Пуанкаре) утверждения в совокупности явным образом никем не рассматривались.

Экспериментальная проверка постулатов СТО в известной степени затруднена проблемами философского плана: возможностью записи уравнений любой теории в инвариантной форме безотносительно к её физическому содержанию, и сложности интерпретации понятий «длина», «время» и «инерциальная система отсчёта» в условиях релятивистских эффектов.

Тем не менее, опора на достижения экспериментальной физики позволяет утверждать, что в пределах своей области применимости — при пренебрежении эффектами гравитационного взаимодействия тел, СТО является справедливой с очень высокой степенью точности (до 10 −12 и выше). По меткому замечанию Л. Пэйджа «В наш век электричества, вращающийся якорь каждого генератора и каждого электромотора неустанно провозглашает справедливость теории относительности — нужно лишь уметь слушать».

Сущность СТО [ править ]

Следствием постулатов СТО являются преобразования Лоренца, заменяющие собой преобразования Галилея для нерелятивистского, «классического» движения. Эти преобразования связывают между собой координаты и времена одних и тех же событий, наблюдаемых из различных инерциальных систем отсчёта.

Именно они описывают такие знаменитые эффекты, как замедление хода времени и сокращение длины быстродвижущихся тел, существование предельной скорости движения тела (коей является скорость света), относительность понятия одновременности (два события происходят одновременно по часам в одной системе отсчета, но в разные моменты времени по часам в другой системе отсчета).

При движении с околосветовыми скоростями видоизменяются также и законы динамики. Так, можно вывести, что второй закон Ньютона, связывающий силу и ускорение, должен быть модифицирован при скоростях тел, близких к скорости света. Кроме того, можно показать, что и выражение для импульса и кинетической энергии тела уже имеет более сложную зависимость от скорости, чем в нерелятивистском случае.

Специальная теория относительности получила многочисленные подтверждения на опыте и является безусловно верной теорией в своей области применимости. Специальная теория относительности перестает работать в масштабах всей Вселенной, а также в случаях сильных полей тяготения, где её заменяет более общая теория — общая теория относительности. Специальная теория относительности применима и в микромире, её синтезом с квантовой механикой является квантовая теория поля.

Символы [ править ]

Символы, которые вдруг могут понадобиться (для составления формул), чтобы не искать их по всей Википедии… Формулы подобраны и составлены так, чтобы наилучшим образом отразить правила их построения:

a sin ⁡ α = b sin ⁡ β = c sin ⁡ γ <\displaystyle >=>=>> ,

p → = ∑ i = 1 n m i v → i 1 − v i 2 / c 2 <\displaystyle <\vec

>=\sum _^<\frac <\vec >_><\sqrt <1-v_^<2>/c^<2>>>>>

Источник