Что такое компьютерная модель объекта
Компьютерное моделирование
Компьютерная модель (англ. computer model ), или численная модель (англ. computational model ) — компьютерная программа, работающая на отдельном компьютере, суперкомпьютере или множестве взаимодействующих компьютеров (вычислительных узлов), реализующая абстрактную модель некоторой системы. Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и проч. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования.
Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить т. н. вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий.
Построение компьютерной модели базируется на абстрагировании от конкретной природы явлений или изучаемого объекта-оригинала и состоит из двух этапов — сначала создание качественной, а затем и количественной модели. Компьютерное же моделирование заключается в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели и т. д.
К основным этапам компьютерного моделирования относятся:
Различают аналитическое и имитационное моделирование. При аналитическом моделировании изучаются математические (абстрактные) модели реального объекта в виде алгебраических, дифференциальных и других уравнений, а также предусматривающих осуществление однозначной вычислительной процедуры, приводящей к их точному решению. При имитационном моделировании исследуются математические модели в виде алгоритма(ов), воспроизводящего функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций.
Содержание
Практическое применение
Компьютерное моделирование применяют для широкого круга задач, таких как:
Различные сферы применения компьютерных моделей предъявляют разные требования к надежности получаемых с их помощью результатов. Для моделирования зданий и деталей самолетов требуется высокая точность и степень достоверности, тогда как модели эволюции городов и социально-экономических систем используются для получения приближенных или качественных результатов.
Информационные модели (схемы, карты, таблицы, графики и формулы)
Теория к заданию 3 из ЕГЭ по информатике
Моделирование и компьютерный эксперимент
Общая структура деятельности по созданию компьютерных моделей
Объект (лат. objectum — предмет) — это некоторая часть окружающего мира, рассматриваемая как единое целое. Все, что человек изучает, использует, производит, является объектом. Каждый объект имеет имя, что позволяет отличить один объект от другого (например, стол, атом, город Москва, ураган Катрин и т. п.). Конкретизировать объект можно с помощью параметров. Параметры — это признаки, которые характеризуют какое-либо свойство объекта. Они могут быть количественные (рост, вес, возраст, размер и т. п.) и качественные (форма, материал, цвет, запах, вкус и т. п.). Очень часто можно наблюдать смену состояний объекта в течение времени и, как результат, изменение параметров объекта. Говорят, что происходит некоторый процесс. Переход объекта из одного состояния в другое происходит при воздействии на него других объектов.
Модель (лат. modulus — мера; франц. modele — образец) — искусственно созданный объект в виде схем, чертежей, логико-математических знаковых формул, компьютерной программы, физической конструкции, который, будучи аналогичен (подобен, сходен) исследуемому объекту (явлению, процессу, устройству, сооружению, механизму, конструкции), отображает и воспроизводит в более простом, уменьшенном виде структуру, свойства, взаимосвязи и отношения между элементами исследуемого объекта, непосредственное изучение которого связано с какими-либо трудностями, большими затратами средств и энергии или просто недоступно, и тем самым облегчает процесс изучения информации об интересующем нас предмете.
Исследуемый объект по отношению к модели является оригиналом (образцом, прототипом). Модели могут создаваться как из однородного с оригиналом материала (например, макет деревянного сооружения можно сделать тоже из дерева), так и из материала, совершенно отличного от материала оригинала (например, бумажная модель самолета). Кроме того, модели могут быть нематериальными, или абстрактными (например, математическая модель самолета, компьютерная модель электрической сети).
Моделирование — это исследование каких-либо объектов (конкретных или абстрактных) на моделях. Объектом моделирования может быть объект, явление или процесс.
При создании модели стараются отразить наиболее существенные свойства объекта, а несущественные свойства отбрасываются. Например, на глобус наносятся океаны и моря, материки и крупные острова, а маленькие озера и островки на него не попадают: в масштабе глобуса они будут просто не видны.
Человек постоянно занимается моделированием, поскольку модели, упрощая объекты и явления, помогают человеку понять реальный мир. Более того, любая наука начинается с разработки простых и адекватных моделей.
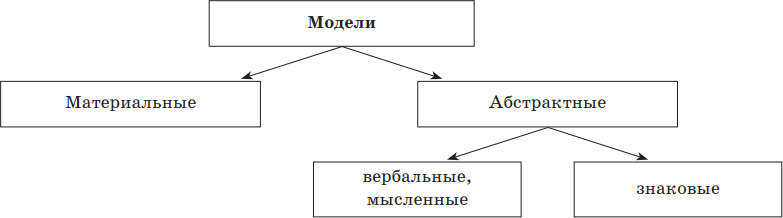
Кроме материальных (предметных) моделей (игрушки, глобуса, макета дома. ), существуют нематериальные — абстрактные модели: описания, формулы, изображения, схемы, чертежи, графики и т. д. С помощью математических формул описываются, например, арифметические операции, соотношения геометрии, законы движения и взаимодействия тел (S = Vt, F = mа) и многое другое. Химические формулы помогают представить молекулярный состав химических веществ и реакции, в которые они вступают. Пользуясь таблицами, графиками, диаграммами можно отображать различные закономерности и зависимости реального мира.
Все абстрактные модели не имеют физического воплощения. Абстрактные модели, которые можно представить с помощью набора знаков (геометрических фигур, символов, фрагментов текста), — это знаковые модели. Любую знаковую модель можно изобразить на бумаге. Чтобы построить знаковую модель, нужно представлять значение знаков и знать правила их преобразования. Абстрактная модель, прежде чем оформиться в виде знаковой модели, сначала рождается в голове человека. Она может передаваться человека к человеку в устной форме. В таких случаях модель еще не является знаковым образом, поскольку не имеет вида чертежа, формулы, текста. Модель в голове человека существует в форме мысленных представлений (мысленная модель). Модели, полученные в результате умозаключений, называются вербальными (лат. verbalis — устный). Вербальными называются также модели, изложенные в разговорной форме. Таким образом, все абстрактные модели можно разделить на знаковые и вербальные.
Представленная классификация моделей самая простая. Она основана на делении моделей по способу представления. Возможны и другие классификации, — например, по предметному признаку: физические, химические модели, модели строительных конструкций, различных механизмов и т. д.
Если модель формулируется таким образом, что ее можно обработать на компьютере, то она называется компьютерной. Компьютерная модель — это модель, реализуемая с помощью программных средств.
Компьютерные модели обычно различают по программному обеспечению, которое применяется при создании и работе с моделью. Для обработки компьютерных моделей используются существующие программные приложения (математические пакеты, электронные таблицы, графические редакторы и т. д.) либо разрабатываются оригинальные программы с помощью языков программирования (Ваsic, Раsсаl, Dеlpi, С++ и др.).
Моделирование с использованием компьютера предоставляет неизмеримо больше возможностей, чем простое моделирование с помощью реальных предметов или материалов. Например, применение компьютера для раскроя (листового металла, ткани и пр.) позволяет снизить до минимума потери материала. Поиск оптимального решения этой задачи с помощью шаблонов потребует значительно больше времени и средств.
Этапы создания модели
Моделирование — творческий процесс, и разложить его на какие-либо этапы и шаги очень сложно. Многие модели и теории рождаются как соединение опыта и интуиции ученого или специалиста. Однако решение большинства конкретных задач все же можно представить поэтапно.
При постановке задачи нужно отразить (или хотя бы понять) цель или мотив создания модели. Одни модели создаются, чтобы разобраться в устройстве или составе того или иного объекта. Другие модели направлены на изучение возможностей управления объектом. Третьи модели ставят целью предсказать поведение объекта (задачи прогнозирования). На этапе постановки задачи полезным оказывается предварительный анализ объекта. Разложение объекта на составляющие, выяснение связей между ними позволяет уточнить постановку задачи.
За постановкой задачи следует этап разработки модели. На этом этапе необходимо выделить существенные факторы, т. е. выяснить основные свойства описываемого объекта, правильно определить связи между ними и с другими объектами окружающего мира. Анализ информации, по возможности, должен быть разносторонним и полным. Те факторы, которые оказались несущественными, могут быть отброшены.
После того как сформулированы основные свойства разрабатываемой модели, определены исходные данные и желаемый результат, наступает очень важный момент — составление алгоритма решения задачи.
При разработке компьютерной модели весьма существенным будет выбор программного обеспечения, с помощью которого выполняется моделирование. Программное обеспечение должно позволять эффективно решать задачи, подобные той, которая рассматривается. Например, для создания рисунка на компьютере нужно выбрать тот или иной графический редактор (какой именно — зависит от требуемого формата файла и приемов, которые необходимо применять при рисовании). Чтобы решить систему уравнений, нужно воспользоваться языками программирования Basic, Pascal или каким-либо другим или же использовать для решения математические пакеты. Программная среда должна соответствовать поставленной задаче — только в этом случае задача может быть успешно решена. Выбор программного обеспечения и составление алгоритма — это взаимосвязанные действия. Возможно, что для решения поставленной задачи придется разработать собственную компьютерную программу.
Когда модель разработана, можно приступать к наиболее интересному этапу — компьютерным экспериментам. В ходе этих экспериментов проверяется работа модели, а также выполняются необходимые расчеты или преобразования, ради которых и создавалась модель.
Проверка модели осуществляется обычно с помощью ее тестирования. При тестировании проверяется разработанный алгоритм функционирования модели. В качестве теста задаются исходные данные, для которых заранее известен ответ. Если ответ, полученный при тестировании, совпадает с известным ответом, а тест составлен правильно, то считается, что модель работает корректно. В противном случае нужно искать и устранять причины расхождений. Все эти действия называются отладкой модели.
После выполнения тестирования и отладки можно приступать непосредственно к моделированию. Технология моделирования может заключаться в расчете модели при различных наборах входных данных, различных параметрах.
Завершается компьютерное моделирование анализом результатов. Материалом для анализа являются результаты компьютерных экспериментов. Поэтому эксперименты должны быть проведены таким образом, чтобы получить достоверный результат. Анализ результатов может привести к необходимости уточнения модели, т. е. к повторному выполнению второго этапа и всех последующих этапов.
Этапы компьютерного моделирования можно представить в виде таблицы.
| 1. ПОСТАНОВКА ЗАДАЧИ | Описание |
| Мотивация | |
| Предварительный анализ |
| 2. РАЗРАБОТКА МОДЕЛИ | Выделение существенных факторов |
| Составление алгоритма | |
| Выбор программного обеспечения | |
| Программирование |
| 3. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ | Тестирование модели |
| Отладка модели | |
| Расчет модели при различных входных данных |
| 4. АНАЛИЗ РЕЗУЛЬТАТОВ |
Представление и считывание данных в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)
Многообразие объектов предполагает использование огромного количества инструментов для реализации и описания этих моделей. Для исследования большинства объектов не обязательно создавать материальные модели. Если ясно представлять цель исследования, то часто достаточно иметь нужную информацию и представить ее в оптимальной форме. В этом случае речь идет о создании информационной модели. Информационные модели — это абстрактные модели, поскольку, как известно, информация — это нематериальная категория.
Информационная модель — это целенаправленно отобранная информация об объекте, представленная в некоторой форме.
Простейшими примерами информационных моделей являются различные загадки, в которых описываются свойства, по которым нужно угадать название объекта («Летом серый, зимой белый»; «Зимой и летом одним цветом»). К информационным моделям можно отнести тексты справочных изданий, энциклопедий.
Формы представления информационных моделей могут быть различными. Наиболее известны следующие формы:
Один и тот же объект, в зависимости от поставленной цели, можно представить несколькими информационными моделями, отличающимися набором параметров и способом их представления. Рассмотрим примеры анализа информации для модели, представленной в табличной форме.
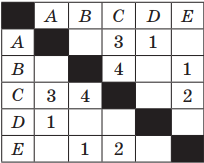
Пример 1. Таблица стоимости перевозок между станциями A, B, C, D, E построена следующим образом: числа, стоящие в ячейках на пересечении строк и столбцов, означают стоимость проезда между соответствующими соседними станциями. Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями. Если на пересечении строки и столбца пусто, то станции не являются соседними. Выбрать таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6».
Решение. Прежде всего, нужно отметить, что данные в таблицах симметричны относительно главной диагонали, т. е. проезд из А в В стоит столько же, сколько и из В в А.
Рассмотрим первую таблицу. Выберем все возможные варианты проезда из А в В и соответственно подсчитаем стоимости: AC(3) + CB(4); AC(3) + CE(2) + EB(2)
Примечание. В скобках указана стоимость проезда.
Стоимость, как первого, так и второго варианта маршрута равна 7.
Аналогично поступим для второй таблицы: AC(3) + CB(4); AE(1) + EC(2) + CB(4).
Как и в случае с предыдущей таблицей, стоимость как первого, так и второго варианта маршрута равна 7.
Выписываем все варианты для третьей таблицы: AC(3) + CB(4); AC(3) + CE(2) + EB(1).
Стоимость последнего варианта маршрута равна 6.
Ответ: таблица номер 3 содержит маршрут из А в В, стоимость которого не превышает 6.
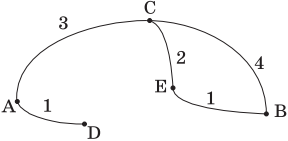
Пример 2. Для заданной информационной модели, записанной в форме таблицы, построить модель в виде схемы. В ячейках на пересечении строк и столбцов таблицы указана стоимость проезда между соседними станциями. Пустые ячейки означают, что станции не являются соседними.
Решение. Отметим точку A, она должна быть соединена с C и D. Отмечаем точки C и D и соединяем их с точкой А дугами; над каждой дугой указываем стоимость проезда. Точка С должна быть соединена, кроме А, с точками В и Е. Точка D является соседней только с А. Точка В должна быть соединена, кроме С, с точкой Е. В результате можно получить следующую схему:
Математические модели (графики, исследование функций)
Знаковые модели принято делить на математические и информационные.
Математическая модель — это знаковая модель, сформулированная на языке математики и логики. Это система математических соотношений — формул, уравнений, неравенств, графиков и т. д., отображающих связи различных параметров объекта, системы объектов, процесса или явления.
Над элементами математической модели можно выполнять определенные математические преобразования. Например, в модели нахождения наименьшего числа выполняются операции сравнения, а в модели вычисления корня уравнения — различные арифметические операции. С помощью математических моделей описываются решения различных инженерных задач, многие физические процессы (движение планет, автомобиля и т. п.); технологические процессы (сварка, плавление металла и т. п.). Графики, таблицы, диаграммы позволяют отображать различные закономерности и зависимости реального мира. Например, модель развития эпидемии можно описать как с помощью формул, так и с помощью графика. Полет снаряда, выпущенного из орудия, можно математически смоделировать с помощью известных формул движения, затем построить график движения снаряда — баллистическую кривую, которая отображает реальный полет снаряда. Математически изменяя параметры снаряда или характеристики движения, можно изучать, например, вопросы увеличения дальности или высоты полета и т. п.
Как известно, не все математические задачи можно решить аналитически, т. е. получить решение в виде формул. Значительно больше задач, которые решаются приближенно, с заданной точностью, т. е. с использованием численных методов. Реализация приближенных расчетов на компьютерах позволяет повысить точность и скорость расчетов.
В настоящее время расчеты для большинства математических моделей проводят на компьютерах, используя специальные прикладные программные комплексы, которые позволяют:
Построение и использование информационных моделей реальных процессов (физических, химических, биологических, экономических)
Моделирование занимает центральное место в исследовании объекта. Компьютеры дают широкие возможности для постановки компьютерных экспериментов. Компьютерное моделирование позволяет воссоздать явления, которые в реальных условиях воспроизвести невозможно. Это, например, движение материков, эффекты землетрясений и наводнений, рождение сверхновых звезд, изменение направлений морских подводных течений и т. д. При изучении этих явлений на помощь приходят компьютеры и компьютерные программы, причем последние составляются квалифицированными программистами совместно с различными специалистами: физиками, географами, биологами, медиками и др.
Компьютерное моделирование используется также при описании и расчете экспериментов, которые выполнять в реальности не следует. Это, например, модели ядерного взрыва, пожара на предприятии, столкновения на железной дороге, военных действий и т. д. С помощью компьютерных моделей можно с достаточной точностью описать детали этих катастроф и спрогнозировать последствия.
Построение моделей позволяет осознанно принимать решения по усовершенствованию имеющихся объектов и созданию новых, изменению процессов управления ими. И, как следствие, наблюдается изменение окружающего нас мира.
Примеры информационных компьютерных моделей для различных отраслей знаний приведены в таблице.
Компьютерное моделирование
Что называется моделью? Для чего необходима модель? Какие бывают компьютерные модели? Что такое вычислительный эксперимент?
1. Модель и ее назначение
2. Классификация компьютерных моделей
Одним из эффективных способов изучения явлений является научный эксперимент, то есть воспроизведение изучаемого явления в контролируемых условиях, которыми можно управлять. Исследуемый объект часто заменяют компьютерной моделью ввиду большей удобности и экономичности. Благодаря распространению мощных ЭВМ и информационных технологий в настоящее время компьютерное моделирование можно назвать самым результативным методом исследования физических, технических и других систем. Компьютерные модели позволяют выявить основные условия, которые определяют свойства изучаемых явлений и объектов, изучить обратную связь системы на изменяющиеся условия.
Компьютерная модель – это отдельная программа либо программный комплекс, которые позволяют при помощи вычислений и графического отображения результатов воспроизводить реальные объекты и процессы при воздействии на них различных факторов. Такие модели еще называют имитационными.
Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе изучения ее компьютерной модели. Смысл такого моделирования состоит в получении количественных и качественных результатов по созданной модели, что позволяет изучить неизвестные ранее свойства системы. Компьютерная модель должна отображать максимальное количество взаимосвязей и характеристик реального объекта, существующие ограничения. Модель следует строить универсальной, чтобы использовать ее для описания подобных объектов; простой, чтобы обойтись разумными тратами на исследование.
Компьютерная модель также является отличным наглядным и обучающим пособием для учащихся. При использовании компьютерной модели в качестве обучающего механизма существуют возможности:
Виды компьютерных моделей.
Для начала определимся, каким может быть компьютерное моделирование.
Исходя из всего вышеперечисленного, компьютерные модели можно разделить на:
Под компьютерным моделированием изначально подразумевалось только имитационное моделирование, однако, не трудно заметить, что использование компьютера для других целей может значительно помочь для решения поставленных задач. Например, построение современных математических моделей по входным экспериментальным данным невозможно или труднодостижимо без использования компьютера.
Первые задач, решаемые с помощью компьютерного моделирования, были связаны с физикой и представляли собой в основном сложные нелинейные задачи физики с помощью итерационных схем и по сути являлось математическим моделированием. Хорошие результаты в моделировании в области физики распространили использование этого метода исследования и на другие области. Сложность решаемых моделированием задач зависела только от мощности используемых компьютеров, тем самым и ограничивалась несовершенными мощностями
После публикации в 1948 году статьи Дж. Неймана и С. Улама, в которой впервые было описано применение метода Монте-Карло, многие исследователи стали называть компьютерное моделирование методами Монте-Карло. Это не верно, правильней будет выглядеть разделение компьютерного моделирования на несколько направлений[6]:
Разновидностью компьютерного моделирования является вычислительный эксперимент, который предполагает дальнейшее численное исследование модели после ее создания, позволяющее исследовать объект в различных его модификациях и при различных условиях.
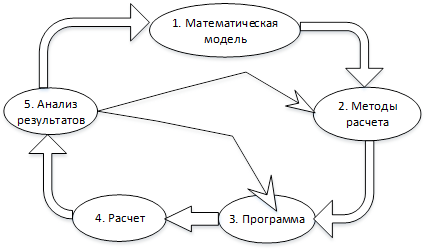
3. Вычислительный эксперимент
С использованием ЭВМ для выполнения арифметических и логических операций производительность интеллектуального труда человека значительно возросла. Первые задачи, для которых создавались ЭВМ, были связаны с ядерной энергией и освоением пространства космоса. Сейчас же компьютер принимает участие в различных задачах и исследованиях, эта технология теоретических экспериментов получила название вычислительного эксперимента. Основой вычислительного эксперимента является математическое моделирование, теоретической базой – прикладная математика, а технической – мощные электронные вычислительные машины.
Компьютерное моделирование и вычислительный эксперимент становятся новым методом научного познания для исследования сложных моделей систем. Цикл вычислительного эксперимента принято разделять на несколько этапов для лучшего восприятия сути этого метода.
Цикл вычислительного эксперимента