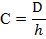Что такое комплексный чертеж

Комплексный чертеж

Комплексным чертежом называется изображение предмета двумя или несколькими его ортогональными проекциями с сохранением проекционной связи.

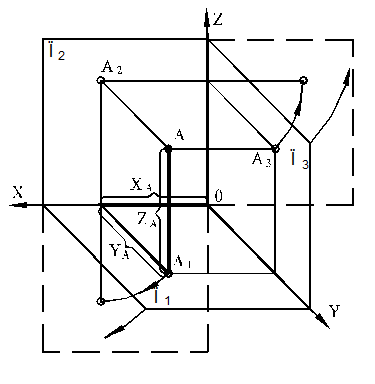
Условие обратимости выполняется ортогональным проецированием объекта на две (П₁, П₂) или три (П₁, П₂, П₃) взаимно перпендикулярные плоскости проекций (см. рисунок 6).

Плоскость П₁ называют горизонтальной плоскостью проекций, П₂ — фронтальной, П₃ — профильной.

Прямые пересечения плоскостей проекций называют осями проекций X,Y,Zили координатными осями; цифрой О обозначена точка пересечения всех трех осей проекций (начало координат).

Рассмотрим образование комплексного чертежа на примере простейшего элемента пространства — точки.

Для построения проекций точки А проведем через нее три проецирующие прямые, перпендикулярные соответствующим плоскостям проекций. Точки А₁, А₂, А₃ пересечения проецирующих прямых с плоскостями проекций будут искомыми проекциями точки А.

Для получения плоского (комплексного) чертежа горизонтальная плоскость проекций П₁ совмещается с фронтальной плоскостью проекций П₂ путем вращения вокруг оси Х. Профильная плоскость П₃ совмещается с фронтальной плоскостью проекций П₂ путем вращения вокруг оси Z. На рисунке показано направление вращения.

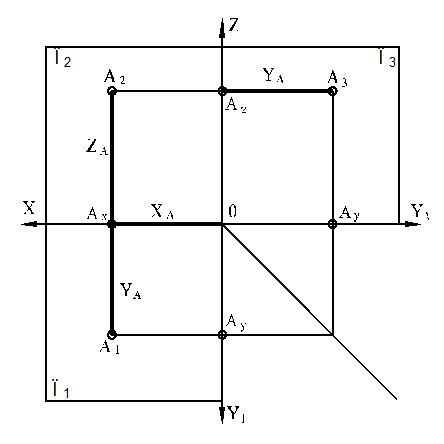
Комплексный чертеж точки представлен на рисунке 7.

Прямые линии, соединяющие проекции дветочки и перпендикулярные осям проекций (X,Y,Z)называют линиями проекционной связи.

Комплексный чертеж обладает следующими свойствами:

— две проекции точки определяют ее положение в пространстве;

— две проекции точки лежат на одной линии связи, перпендикулярной оси проекций;

— по двум проекциям точки можно построить третью;

— удаление точки от плоскости П₁ определяет координата Z, от плоскости П₂ — Y, от плоскости П₃ — X.

Источник

Что такое комплексный чертеж

§ 18. Комплектный чертеж

Изучив, как в прямоугольных проекциях изображают точки, отрезки прямых и плоские фигуры, т. е. элементы, которые образуют различные предметы, рассмотрим способы получения прямоугольных проекций самих предметов.

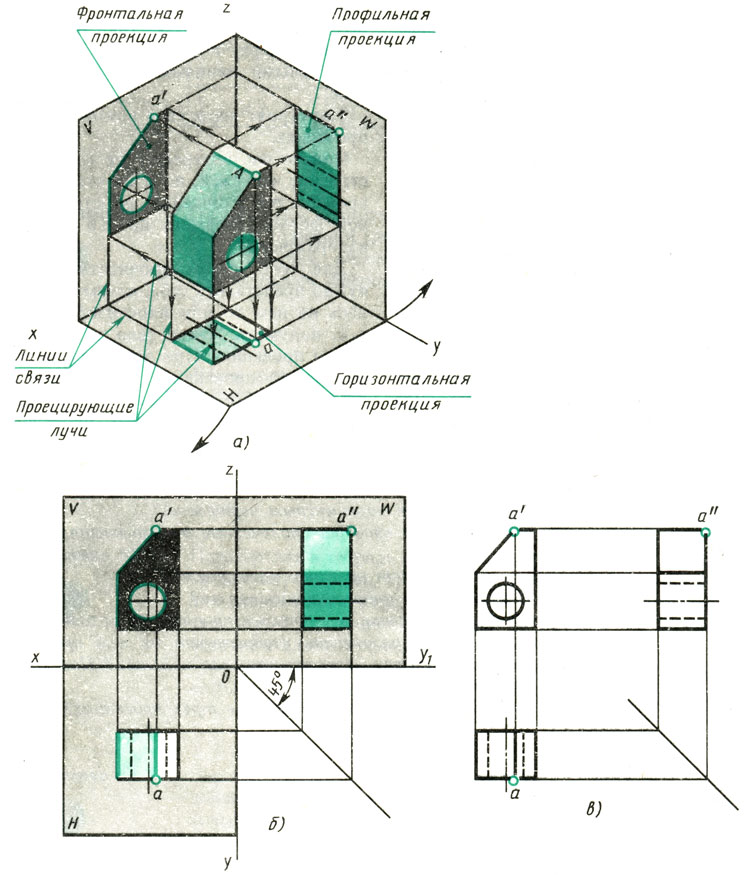
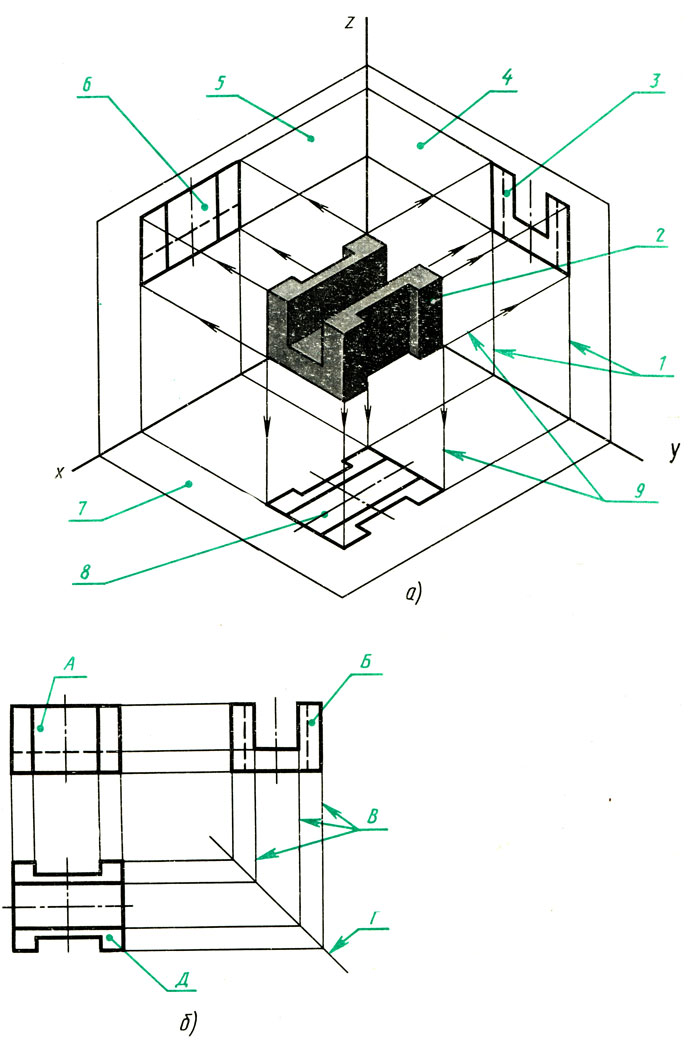
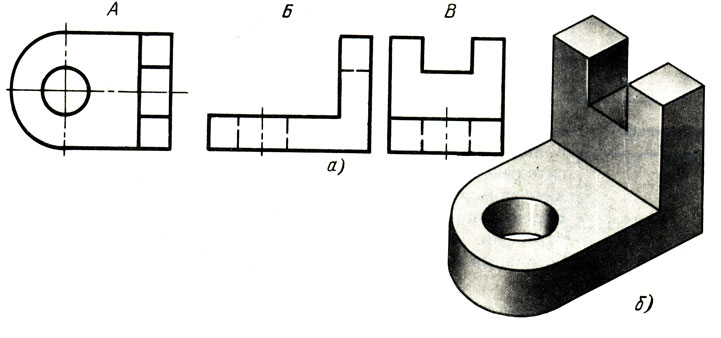
Изображаемый предмет располагают перед плоскостями трехгранного угла так, чтобы возможно большее число граней предмета было параллельно плоскостям (рис. 112, а). Предмет проецируют на фронтальную плоскость V. Грани, параллельные плоскости V, изобразятся в натуральную величину, а грани, перпендикулярные к плоскости V,- отрезками прямых линий. Ребра, параллельные плоскости V, изобразятся в виде линии в натуральную длину, а ребра, перпендикулярные плоскости F,- точками. Так получают фронтальную проекцию предмета или вид спереди (см. рис. 112, а). Тем же способом на плоскости Н получают горизонтальную проекцию (вид сверху). Профильная проекция предмета (вид слева) расположится на плоскости W. Развернув плоскости проекции, получают комплексный чертеж (рис. 112, в).

Рис. 112. Получение комплексного чертежа

Фронтальную проекцию называют видом спереди, или главным видом. Главный вид, получаемый на фронтальной плоскости проекций, является исходным, он должен давать наиболее полное представление о форме и размерах предмета. Остальные проекции располагаются в зависимости от главного вида. Такое расположение проекций называют проекционной связью.

Проекционная связь показана на рис. 112, б и в тонкими сплошными линиями, которые называются линиями связи.

При проведении линий связи между горизонтальной и профильной проекциями удобно пользоваться вспомогательной прямой, которую проводят под углом 45° примерно на уровне вида сверху, правее его (рис. 112, б и в). Линии связи, идущие от вида сверху, доводят до вспомогательной прямой. Из точек пересечения с нею восставляют перпендикуляры для построения вида слева.

Чтобы сократить число изображений, допускается на видах показывать невидимые части поверхности предмета штриховыми линиями. Так, например, на виде сверху и слева (рис. 112, б и в) штриховыми линиями показано отверстие.

Так строят чертежи в прямоугольных проекциях.

Однако нас интересует не только построение чертежей, но и их чтение, т. е. процесс представления пространственной формы предмета по его плоским изображениям.

Для того чтобы прочитать чертеж, нужно представить себе, почему получилось на нем то или иное изображение, т. е. подумать, какое тело могло дать такую проекцию. При этом нельзя рассматривать проекции отдельно одну от другой. Необходимо мысленно объединить представления о всех проекциях, данных на чертеже.

Ответьте на вопросы

1. Что называют комплексным чертежом?

2. Как называют проекции, полученные на плоскостях V, Н, W?

3. Как располагают проекции на чертеже?

4. Что означает «проекционная связь»?

5. Какое изображение на чертеже принято за исходное (основное)? В каком положении изображают на нем предмет?

6. Для чего служит «вспомогательная прямая»? Под каким углом ее проводят?

7. Как строят чертеж: предмета в трех проекциях?

Задания к § 17 и 18

Упражнение 50

Рассмотрите рис. 113, а и б. Выпишите в рабочую тетрадь названия плоскостей проекций, изображений и других элементов прямоугольного проецирования, помеченных на рис. 113 цифрами или буквами.

Форма записи:

Рис. 113. Задание для упражнений

Упражнение 51

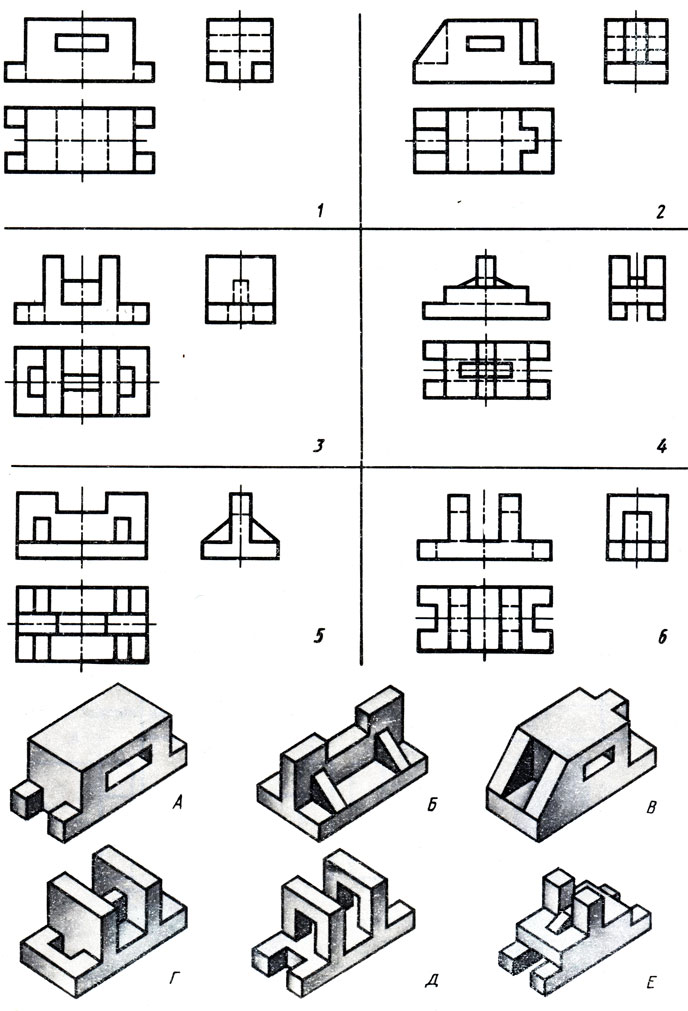
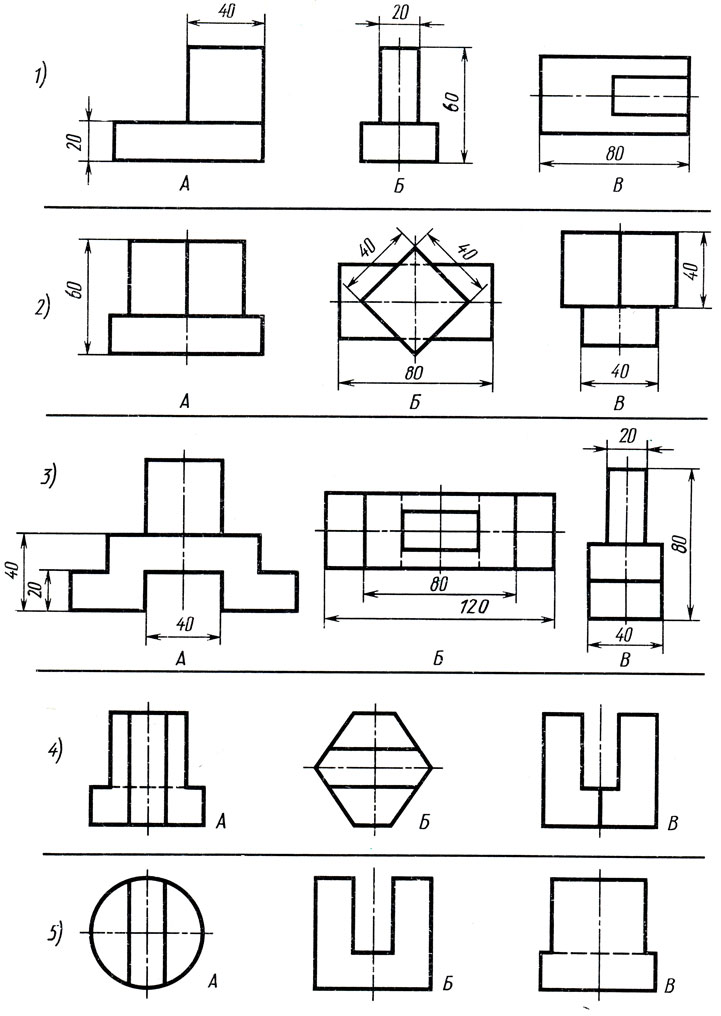
По рисункам предметов найдите их чертежи в системе прямоугольных проекций (рис. 114). Запишите в рабочей тетради, какому рисунку, обозначенному буквой, соответствует чертеж, обозначенный цифрой. Как называют виды, данные на чертеже?

Форма записи:

Рис. 114. Задание для упражнений

Упражнение 52

Перечертите в тетрадь рис. 112, в в масштабе 2 : 1. Дайте к этому рисунку подпись, кратко изложите в ней основные положения данного параграфа (что называют комплексным чертежом, что значит проекционная связь, под каким углом проводят вспомогательную прямую и каково ее назначение, как обозначают проекции точек, как строят комплексный чертеж). В начале работы напишите заголовок «Комплексный чертеж».

Упражнение 53

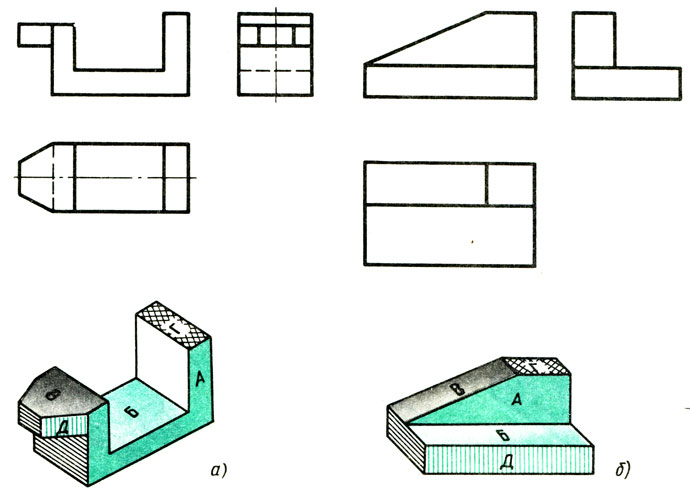
Перечертите рис. 115, я и б в масштабе 2 : 1. Раскрасьте на каждой из прямоугольных проекций одну и ту же поверхность одинаковым цветом. (Поверхность надо раскрасить цветным карандашом или краской на всех проекциях независимо от того, изображается она фигурой или линией.)

Рис. 115. Задание для раскрашивание проекций

Упражнение 54

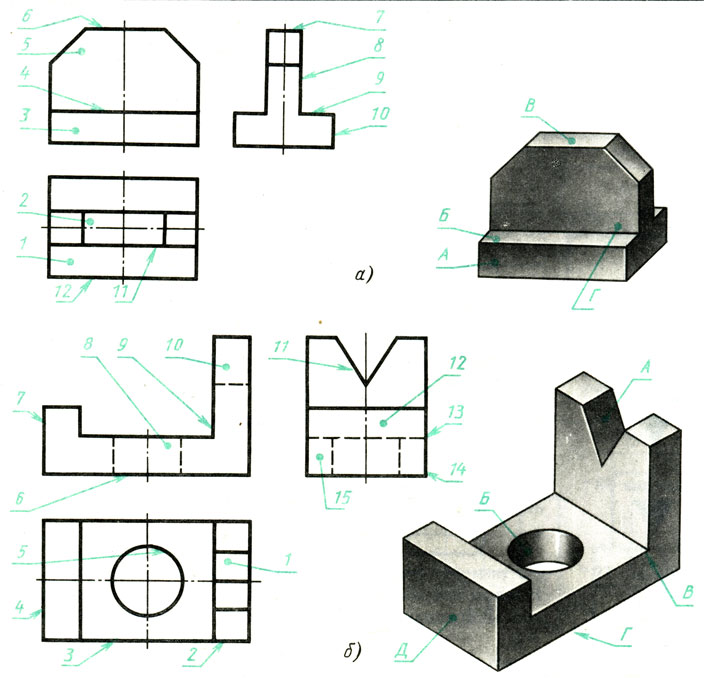
Определите и запишите в рабочей тетради, какой поверхности детали, обозначенной буквой на наглядном изображении, соответствуют линии и фигуры, обозначенные цифрами на чертеже (рис. 116, а и б).

Форма записи

Рис. 116. Задание на нахождение проекций поверхностей предметов

Упражнение 55

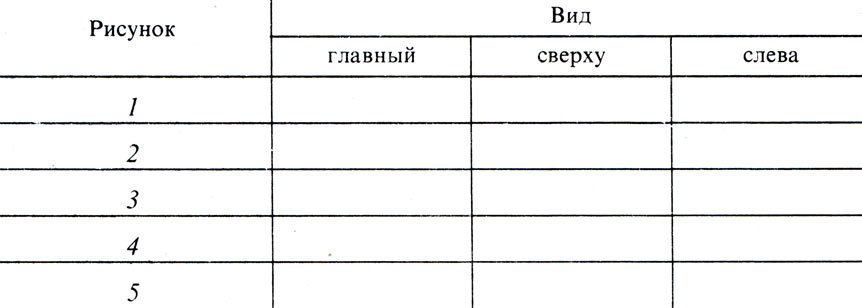
На рис. 117, а виды расположены без системы. Определите, какой буквой помечен главный вид. Как относительно главного вида должны быть расположены остальные виды? Решить задачу вам поможет наглядное изображение, приведенное на рис. 117, б.

Рис. 117. Задание на расположение видов чертежа в проекцтонной связи

Упражнение 56

Форма записи:

Рис. 118. Задания на определение видов и правильное их расположение не чертеже

Упражнение 57

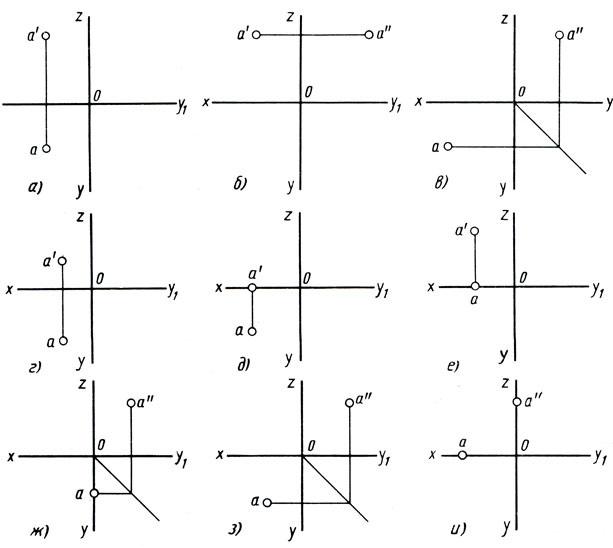
По заданным двум проекциям точек (рис. 119, а-и) найдите ушш третьи проекции. Обозначьте их буквами.

Рис. 119. Задание на построение третьих проекций точек

Упражнение 58

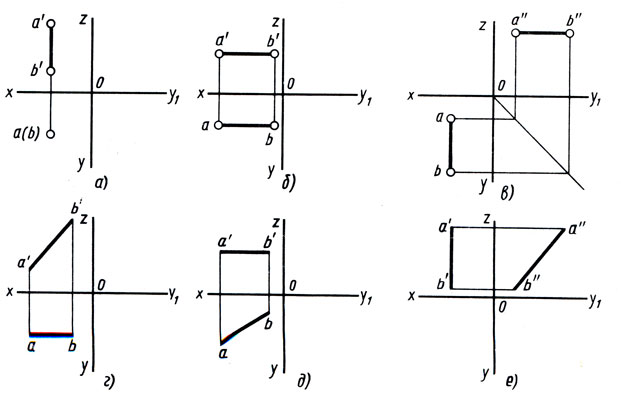
По заданным двум проекциям отрезков прямых (рис. 120, а-е) найдите третьи проекции. Обозначьте их буквами.

Рис. 120. Задания на построение третьих проекций линий

Упражнение 59

Форма записи:

Рис. 121. Задания на выбор положения детали для главного вида

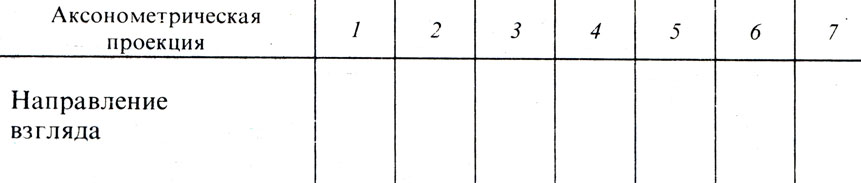
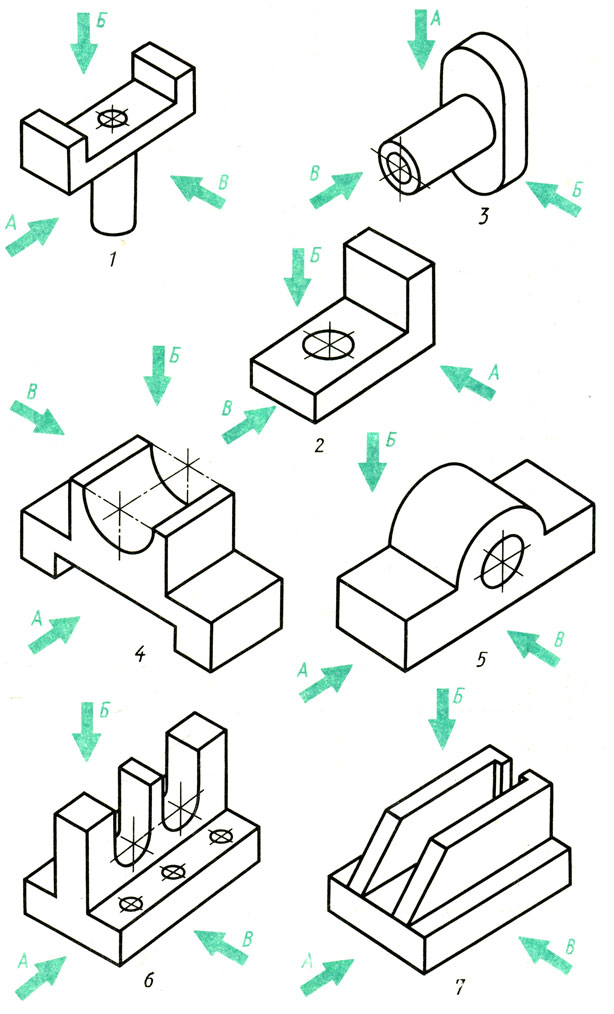
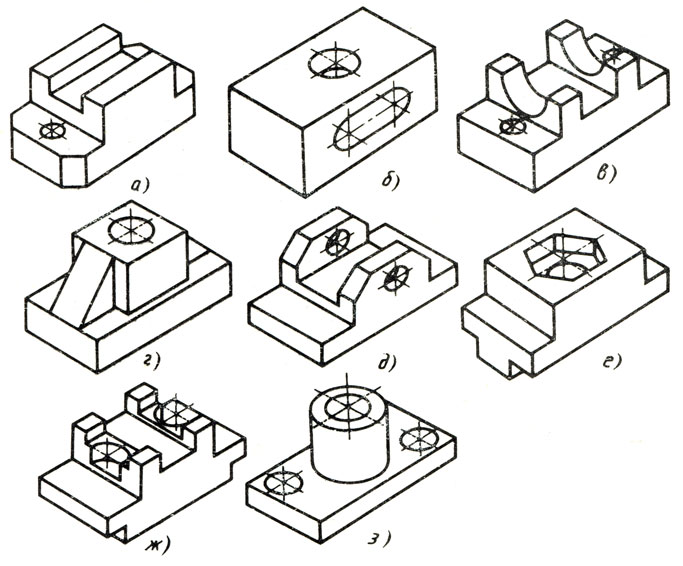
Упражнение 60

Рис. 122. Задания на построение комплексных чертежей по аксонометрическим проекциям

Упражнение 61

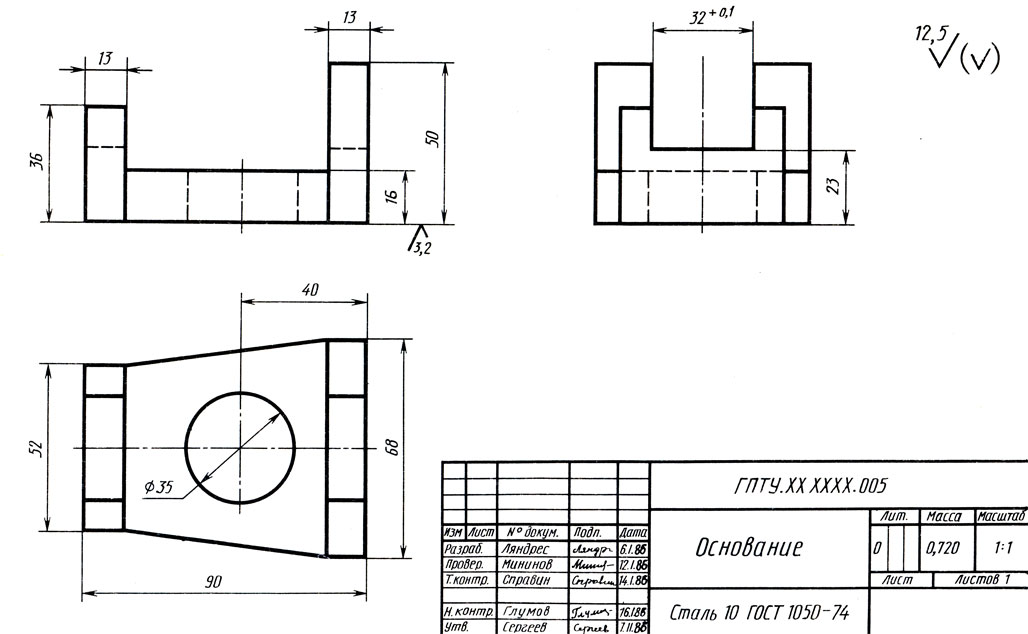
Письменно ответьте на вопросы к рис. 123 (вопросы не переписывайте):

Рис. 123. Задания для упражнений

1. Как называется деталь?

2. Из какого материала ее надо изготовить?

3. В каком масштабе выполнен чертеж?

4. Какие виды даны на чертеже?

6. Каковы габаритные размеры детали?

7. Какова шероховатость поверхности отверстия? Какими размерами определяется положение отверстия?

8. Какова шероховатость основания детали?

9. Что изображено горизонтальной штриховой линией на виде слева? На каком расстоянии от основания детали проходит эта линия? Почему края этой линии заканчиваются отрезками сплошной основной линии, а не штриховой?

Источник

Что такое комплексный чертеж и каковы правила его применения.

Введение………………………………………………………………………………………………. 2 1.1 Как образуются дополнительные форматы чертежей. 2 1.2 Что называется сопряжением, уклоном и конусностью…. 3 1.3 Что такое комплексный чертеж и каковы правила его применения…. 5 1.4 На какие виды делятся аксономентрические проекции в зависимости от направления лучей. 6 1.5 Какое изображение называется видом и сколько их может быть. 7 1.6 Что такое разрез, с какой целью он выполняется…. 9 1.7 Как делятся разрезы в зависимости от числа секущих плоскостей, участвующих в разрезе. 10 1.8 Какое изображение называется сечением, какое оно бывает. 13 1.9 Что такое технический рисунок, и чем он отличается от художественного. 16 1.10 Какие виды конструкторской документации установлены гостом ГОСТ 2.102. – 68…………17 1.11 Составьте таблицу: «Виды резьб»…………………………………………………………………19 1.12 Выполните таблицу: «Условные графические обозначения в кинематических схемах». …. 20 2. Список используемой литературы…………………………………..………………………………26

Введение

Как образуются дополнительные форматы чертежей.

Обозначения и размеры сторон основных и дополнительных форматов
по ГОСТ 2.301-68

ОбозначениеРазмеры сторон, ммОбозначениеРазмеры сторон, ммА0841 х 1189А0 х 2 А0 х 31189 х 1692 1189 х 2523А1594 х 841А1 х 3 А1 х 4841 х 1783 841 х 2378А2420 х 594А2 х 3 А2 х 4 А2 х 5594 х 1261 594 х 1682 594 х 2102А3297 х 420А3 х 3 А3 х 4 А3 х 5 А3 х 6 А3 х 7420 х 891 420 х 1189 420 х 1486 420 х 1783 420 х 2080А4210 х 297А4 х 3 А4 х 4 А4 х 5 А4 х 6 А4 х 7 А4 х 8 А4 х 9297 х 630 297 х 841 297 х 1051 297 х 1261 297 х 1471 297 х 1682 297 х 1892А5148 х 210——

Примечание. Формат А5 допускается применять при необходимости.

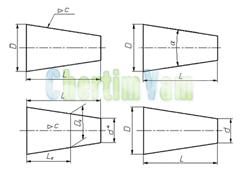
1.2 Что называется сопряжением, уклоном и конусностью.

В очертаниях различных геометрических форм часто встречаются плавные переходы от одной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, как правило, дуги окружности называется сопряжением.

Построение сопряжений основано на следующих положениях геометрии.

Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной t к окружности (рис. 1, а). Радиус окружности r, проведенный в точку касания К, перпендикулярен к касательной прямой.

Рис. 1

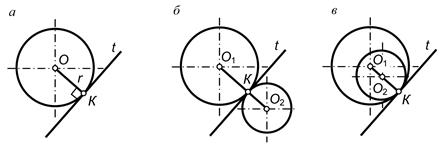
Переход от одной окружности к другой окружности в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную. Точка касания К и центры окружностей O₁ и О₂ лежат на одной прямой. Если центры окружностей лежат по разные стороны от касательной t, то касание называется внешним (рис. 16, б); если центры O₁ и О₂находятся по одну сторону от общей касательной — соответственно внутренним (рис. 1, в).

В теории сопряжений применяются следующие термины (рис. 2):

· центр сопряжения — точка О, равноудаленная от сопрягаемых линий;

· точки сопряжения К₁и К₂ — точки касания двух сопрягаемых линий;

· дуга сопряжения К₁К₂— это дуга окружности, с помощью которой выполняется сопряжение;

· радиус сопряжения R — это радиус дуги сопряжения.

Рис. 2

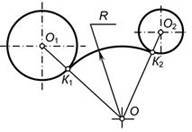
В общем случае построение сопряжения двух линий при заданном радиусе сопряжения состоит из следующих этапов:

1) построение множества точек, находящихся на расстоянии радиуса сопряжения от первой из сопрягаемых линий;

2) построение множества точек, находящихся на расстоянии радиуса сопряжения от второй из сопрягаемых линий;

3) определение на пересечении центра сопряжения;

4) определение точки сопряжения на первой из сопрягаемых линий;

5) определение точки сопряжения на второй из сопрягаемых линий;

6) проведение дуги сопряжения в интервале между точками сопряжения.

Уклон — это величина, характеризующая наклон одной прямой ли­нии к другой прямой.

Уклон отрезка АВ задают отношением катетов прямоугольного треугольника АВС (рис. 3, а) или в процентах (рис. 3, б)

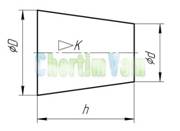
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле С=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: С = (D-d)/h.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Что такое комплексный чертеж и каковы правила его применения.

Комплексным чертежом называется изображение предмета двумя или несколькими его ортогональными проекциями с сохранением проекционной связи.

Условие обратимости выполняется ортогональным проецированием объекта на две (П₁, П₂) или три (П₁, П₂, П₃) взаимно перпендикулярные плоскости проекций (см. рисунок 5).

Плоскость П₁ называют горизонтальной плоскостью проекций, П₂ — фронтальной, П₃ — профильной.

Прямые пересечения плоскостей проекций называют осями проекций X,Y,Zили координатными осями; цифрой О обозначена точка пересечения всех трех осей проекций (начало координат).

Рисунок 5

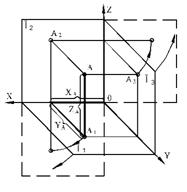
Рассмотрим образование комплексного чертежа на примере простейшего элемента пространства — точки.

Для построения проекций точки А проведем через нее три проецирующие прямые, перпендикулярные соответствующим плоскостям проекций. Точки А₁, А₂, А₃ пересечения проецирующих прямых с плоскостями проекций будут искомыми проекциями точки А.

Для получения плоского (комплексного) чертежа горизонтальная плоскость проекций П₁ совмещается с фронтальной плоскостью проекций П₂путем вращения вокруг оси Х. Профильная плоскость П₃ совмещается с фронтальной плоскостью проекций П₂ путем вращения вокруг оси Z. На рисунке показано направление вращения.

Комплексный чертеж точки представлен на рисунке 6.

Прямые линии, соединяющие проекции две точки и перпендикулярные осям проекций (X,Y,Z)называют линиями проекционной связи.

Рисунок 6

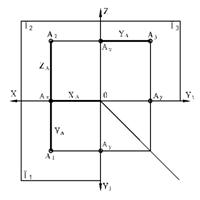
Комплексный чертеж обладает следующими свойствами:

— две проекции точки определяют ее положение в пространстве;

— две проекции точки лежат на одной линии связи, перпендикулярной оси проекций;

— по двум проекциям точки можно построить третью;

— удаление точки от плоскости П₁ определяет координата Z, от плоскости П₂ — Y, от плоскости П₃ — X.

Способом параллельного проецирования можно получить аксонометрические проекции.

Дата добавления: 2018-05-12 ; просмотров: 4958 ; Мы поможем в написании вашей работы!

Источник

Комплексный чертеж

Проецирование объекта на две или более плоскости проекций позволяет однозначно определить положение его точек в пространстве. Получаемый при этом чертеж объекта называют комплексным чертежом в ортогональных проекциях или комплексным чертежом.

Принцип построения комплексного чертежа состоит в том, что объект проецируется ортогонально на две взаимно перпендикулярные плоскости проекций. Одна из плоскостей проекций П₁ располагается горизонтально и называется горизонтальной плоскостью проекций (рис. 1.8). Плоскость П₂ располагается вертикально, ее называют фронтальной плоскостью проекций. Плоскости П₁ и П₂ бесконечны и непрозрачны. Линия пересечения плоскостей проекций называется осью проекцийи обозначаетсяx₁₂. Плоскости проекций делят пространство на четыре двухгранных угла – четверти, нумерация которых приведена на рис. 1.8.

При ортогональном проецировании считают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

При построении проекций необходимо помнить, что ортогональной проекцией точки на плоскость проекций является основание перпендикуляра, опущенного из данной точки на эту плоскость проекций.

Спроецируем ортогонально на плоскости проекций П₁ и П₂ какую-нибудь точку А, тогда получим:

А₁ –горизонтальную проекцию точки А на плоскости П₁;

А₂ – фронтальную проекцию точки А на плоскости П₂.

Множество проекций точек пространства на каждой из плоскостей проекций называется полем проекций.

Чтобы получить плоский чертеж, поле проекций на П₁ поворачивается на 90 ° до совмещения с полем проекций на П₂ (рис. 1.9). Убрав искусственные границы плоскостей П₁ и П₂ (эти плоскости безграничны, на рис. 1.9 границы даны для наглядности), получаем комплексный чертеж точки А (рис. 1.10), где:

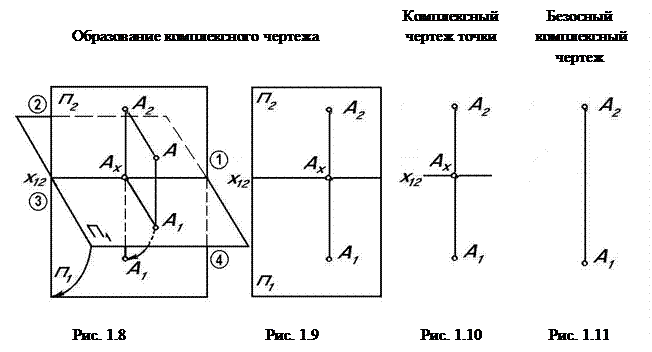
А₁ А₂ – линия проекционной связи – прямая, перпендикулярная оси проекций x₁₂;

|А₁ А_х| – глубина точкиА – расстояние от нее до фронтальной плоскости проекций П₂;

|А₂ А_х| – высота точкиА – расстояние от нее до горизонтальной плоскости проекций П₁.

Полученный комплексный чертеж обладает свойством обратимости, т. е. по нему можно определить или, как говорят, реконструировать оригинал. Применительно к нашему случаю (рис. 1.10) надо восстановить перпендикуляр к плоскости чертежа в его точке А₂ и от плоскости чертежа отложить глубину |А₁ А_х| искомой точки, тогда конец перпендикуляра определит положение точки А.

Рассмотренный принцип образования комплексного чертежа получил со времен Гаспара Монжа широкое распространение в учебной литературе. Однако в технической практике нет необходимости в определении положения изображаемого оригинала относительно неподвижной системы плоскостей проекций. Поэтому при разработке комплексного чертежа можно отказаться от фиксации плоскостей проекций и получить безосный комплексный чертеж (рис. 1.11.)

Источник