Что такое кольцо в математике простыми словами

Группы, кольца, поля в математике

Группа: определение и примеры групп

Множество с алгебраической операцией называется группой, если выполняются следующие условия:

1) операция в ассоциативна: ;

2) в существует нейтральный элемент ;

Решение. Действительно, операция умножения определена на указанном множестве, так как

Кольцо

1) относительно операции сложения множество — коммутативная группа, т.е.

а) операция сложения коммутативна: ;

б) операция сложения ассоциативна: ;

в) существует нулевой элемент ;

г) для каждого элемента существует противоположный ему элемент ;

2) операция умножения в множестве ассоциативна:

3) операции сложения и умножения связаны законами дистрибутивности:

Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.

Если операция коммутативна, то дистрибутивность слева операции относительно операции влечет дистрибутивность справа, так как

Решение. В самом деле, для любых положительных действительных чисел справедливы равенства

Следовательно, операция дистрибутивна справа относительно операции умножения чисел. Дистрибутивность слева относительно умножения опровергается примером

Пример В.7. Доказать, что множество чисел вида, где и — целые числа, является кольцом:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.2) имеют тоже самое представление:

Таким образом, рассматриваемое множество удовлетворяет всем условиям определения кольца.

Поле: определение и примеры полей

1) — коммутативное кольцо с единицей ;

Как видим, поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.

Пример В.8. На множестве трех целых чисел определим две операции:

1) «сложение по модулю 3» — остаток от деления суммы на 3 (обозначим через );

2) «умножение по модулю 3» — остаток от деления произведения на 3 (обозначим через ).

Доказать, что множество является полем относительно введенных операций.

– остаток от деления на 3 суммы не изменится, если слагаемое (или не сколько слагаемых) заменить его остатком при делении на 3:

– остаток от деления на 3 произведения не изменится, если множитель (или несколько множителей) заменить его остатком при делении на 3:

Рассматриваемые в примере операции «сложения по модулю 3» и «умножения по модулю 3» можно представить в виде

Покажем, что множество является коммутативным кольцом с единицей. В самом деле, операция «сложения по модулю 3» коммутативна и ассоциативна. Это следует из коммутативности и ассоциативности сложения чисел. Действительно, из равенства следует, что

Коммутативность доказана. Заметим, впрочем, что коммутативность «сложения по модулю 3» видна непосредственно по таблице (см. рис.В.2): слагаемые и в таблице можно поменять местами, при этом таблица не изменится.

Из равенства следует, что

Ассоциативность «сложения по модулю 3» доказана.

Итак, множество относительно операции «сложения по модулю 3» является коммутативной группой.

Операция «умножение по модулю 3» ассоциативна и коммутативна, что следует из ассоциативности и коммутативности умножения целых чисел, а также свойств остатков:

Следовательно, операция «умножения по модулю 3» дистрибутивна слева относительно операции «сложения по модулю 3». Дистрибутивность справа можно не проверять, так как обе операции коммутативны.

Единичным элементом служит число 1 (что видно по таблице «умножения по модулю 3»). Следовательно, — коммутативное кольцо с единицей.

Пример В.9. Доказать, что множество чисел вида, где и — рациональные числа, является полем:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.З) имеют тоже самое представление:

Так как рассматриваемое множество является коммутативным кольцом с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно является полем.

Источник

Кольцо (математика)

В различных разделах математики, а также в применении математики в технике, часто встречается ситуация, когда алгебраические операции производятся не над числами, а над объектами иной природы. Например сложение матриц, умножение матриц, сложение векторов, операции над многочленами, операции над линейными преобразованиями и т.д.

Определение 1. Кольцом называется множество математических объектов, в котором определены два действия − «сложение» и «умножение», которые сопоставляют упорядоченным парам элементов их «сумму» и «произведение», являющиеся элементами того же множества. Данные действия удовлетворяют следующим требованиям:

1. a+b=b+a (коммутативность сложения).

2. (a+b)+c=a+(b+c) (ассоциативность сложения).

3. Существует нулевой элемент 0 такой, что a+0=a, при любом a.

4. Для любого a существует противоположный элемент −a такой, что a+(−a)=0.

5. (a+b)c=ac+bc (левая дистрибутивность).

5′. c(a+b)=ca+cb (правая дистрибутивность).

Требования 2, 3, 4 означают, что множество математических объектов образует группу, а вместе с пунктом 1 мы имеем дело с коммутативной (абелевой) группой относительно сложения.

Как видно из определения, в общем определении кольца на умножения не накладывается никаких ограничений, кроме дистрибутивности со сложением. Однако при различных ситуациях возникает необходимость рассматривать кольца с дополнительными требованиями.

6. (ab)c=a(bc) (ассоциативность умножения).

7. ab=ba (коммутативность умножения).

8. Существование единичного элемента 1, т.е. такого a·1=1·a=a, для любого элемента a.

9. Для любого элемента элемента a существует обратный элемент a −1 такой, что aa −1 =a −1 a=1.

В различных кольцах 6, 7, 8, 9 могут выполняться как отдельно так и в различных комбинациях.

Кольцо называется ассоциативным, если выполняется условие 6, коммутативным, если выполнено условие 7, коммутативным и ассоциативным если выполнены условия 6 и 7. Кольцо называется кольцом с единицей, если выполнено условие 8.

1. Множество квадратных матриц.

Действительно. Выполнение пунктов 1-5, 5′ очевидна. Нулевым элементом является нулевая матрица. Кроме этого выполняется пункт 6 (ассоциативность умножения), пункт 8 (единичным элементом является единичная матрица). Пункты 7 и 9 не выполняются т.к. в общем случае умножение квадратных матриц некоммутативна, а также не всегда существует обратное к квадратной матрице.

2. Множество всех комплексных чисел.

3. Множество всех действительных чисел.

4. Множество всех рациональных чисел.

5. Множество всех целых чисел.

Примеры 2-5 являются числовыми кольцами. Числовыми кольцами являются также все четные числа, а также все целые числа делящихся без остатка на некоторое натуральное число n. Отметим, что множество нечетных чисел не является кольцом т.к. сумма двух нечетных чисел является четным числом.

Источник

Кольцо (алгебра)

Содержание

Определения

Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:

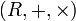
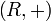
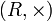
Иными словами, кольцо — это универсальная алгебра , такая что алгебра — абелева группа, алгебра — полугруппа и операция + дистрибутивна относительно .

Ассоциативные кольца могут обладать следующими дополнительными свойствами:

Кольца, для которых выполнены все вышеперечисленные условия, называются целостными (иногда также областями целостности или просто областями, хотя условие коммутативности не всегда считается обязательным).

Иногда под ассоциативным кольцом понимают ассоциативное кольцо с единицей. Но имеются примеры ассоциативных колец без единицы, например — нулевое кольцо, кольцо чётных чисел, или же любой несобственный идеал в кольце. Рассматриваются также неассоциативные кольца без единицы, например лиевские кольца и др.

Связанные определения

Простейшие свойства

Пусть R — кольцо, тогда выполнены следующие свойства:

Примеры

См. также

Ссылки

Полезное

Смотреть что такое «Кольцо (алгебра)» в других словарях:

Простое кольцо (алгебра) — Содержание 1 Определение 2 Примеры и теоремы 3 Теорема Веддербёрна Артина … Википедия

*-алгебра — (алгебра с инволюцией, алгебра с операцией сопряжения) ассоциативная алгебра с инволюцией, которая имеет свойства подобные комплексному сопряжению. Содержание 1 * кольцо 2 * алгебра 3 C* алгебра … Википедия

АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия

Кольцо (множество) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия

Кольцо алгебраическое — Кольцо алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия

Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия

Алгебра Хопфа — Алгебра Хопфа алгебра, являющаяся унитарной ассоциативной коалгеброй и, таким образом, биалгеброй c антигомоморфизмом специального вида. Названа в честь Х. Хопфа. Алгебры Хопфа встречаются в алгебраической топологии, где они возникли в… … Википедия

Алгебра Темперли — Алгебра Темперли Либа, в статистической механике алгебра, при помощи которой строятся некоторые трансфер матрицы. Открыты Невиллом Темперли и Эллиотом Либом. Также алгебра применяется в теории интегрируемых моделей, имеет отношение… … Википедия

АЛГЕБРА С ДЕЛЕНИЕМ — алгебра Анад полем F, для любых элементов и bк рой уравнения разрешимы в А. Ассоциативная А. с д., рассматриваемая как кольцо, является телом, а ее центр С полем и Если то А. с д. Аназ. центральной А. с д. Конечномерные центральные ассоциативные… … Математическая энциклопедия

КОЛЬЦО С ДЕЛЕНИЕМ — кольцо (не обязательно ассоциативное), в к ром для любых элементов аи b, где уравнения ах=b, уа=b обладают решениями. Если решения этих уравнений определены однозначно, то К. с д. наз. квазителом. Квазитело, в отличие от произвольного К. с д., не … Математическая энциклопедия

Источник

Кольцо (математика)

В абстрактной алгебре кольцо́ — это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных, комплексных, …), функций на множестве (всех, непрерывных, гладких, аналитических, …) и матриц. Во всех случаях имеется множество, похожее на множество чисел, в том смысле что его элементы можно складывать и умножать, причём эти операции ведут себя естественным образом. Однако есть и существенные отличия. Уже на примере целых чисел видно, что операция умножения может быть необратимой (операция деления определена не на целых числах, а на рациональных). Это различие ещё более существенно в кольцах функций и матриц: в них существуют элементы, произведение которых равно 0. Например, квадрат матрицы равен 0, так что она в принципе не может иметь обратную. Кроме того, умножение матриц не коммутативно. Алгебры Ли являются важными примерами колец, в которых умножение не ассоциативно и не имеет единицы (тождественного по умножению элемента). Понятие кольца формализует общие свойства всех указанных примеров, позволяя изучать их общими абстрактными методами.

Заметим, что, согласно алгебраической геометрии, любое коммутативное ассоциативное кольцо с единицей можно рассматривать как кольцо функций на некотором пространстве (аффинной схеме), однако соответствующая конструкция весьма нетривиальна, а её результат сложнее, чем может подсказывать элементарная интуиция. Хотя в целом интуитивное представление о кольце как о некотором кольце функций или кольце матриц не слишком сильно искажает истину, необходимо помнить о различиях.

Содержание

Определения

Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:

Иными словами, кольцо — это универсальная алгебра , такая что алгебра — абелева группа, и операция дистрибутивна слева и справа относительно . Кольцо называется ассоциативным, если мультипликативный группоид является полугруппой.

Ассоциативные кольца могут обладать следующими дополнительными свойствами:

Кольца, для которых выполнены два последние свойства, называются целостными (иногда также областями целостности или просто областями, хотя условие коммутативности не всегда считается обязательным).

Иногда под ассоциативным кольцом понимают ассоциативное кольцо с единицей. Но имеются примеры ассоциативных колец без единицы, например — нулевое кольцо, кольцо чётных чисел, или же любой несобственный идеал в кольце. Рассматриваются также неассоциативные кольца без единицы, например лиевские кольца и др.

Связанные определения

Простейшие свойства

Пусть — кольцо, тогда выполнены следующие свойства:

Источник

Кольца, тела, поля

Определение 2.5. Кольцом называют алгебру сигнатура которой состоит из двух бинарных и двух нульарных операций, причем для любых выполняются равенства:

Операцию называют сложением кольца, операцию умножением кольца, элемент — нулем кольца, элемент — единицей кольца.

Равенства 1–7, указанные в определении, называют аксиомами кольца. Рассмотрим эти равенства с точки зрения понятия группы и моноида.

Связь между сложением кольца и умножением кольца устанавливает аксиома 7, согласно которой операция умножения дистрибутивна относительно операции сложения.

Замечание 2.2. В литературе встречается иной состав аксиом кольца, относящихся к умножению. Так, могут отсутствовать аксиома 6 (в кольце нет 1) и аксиома 5 (умножение не ассоциативно). В этом случае выделяют ассоциативные кольца (к аксиомам кольца добавляют требование ассоциативности умножения) и кольца с единицей. В последнем случае добавляются требования ассоциативности умножения и существования единицы.

Определение 2.6. Кольцо называют коммутативным, если его операция умножения коммутативна.

Пример 2.12. а. Алгебра есть коммутативное кольцо. Отметим, что алгебра кольцом не будет, поскольку — коммутативный моноид, но не группа.

в. Алгебра — коммутативное кольцо, что следует из свойств пересечения и симметрической разности множеств.

г. Пример некоммутативного кольца дает множество всех квадратных матриц фиксированного порядка с операциями сложения и умножения матриц. Единицей этого кольца является единичная матрица, а нулем — нулевая.

д. Пусть — линейное пространство. Рассмотрим множество всех линейных операторов, действующих в этом пространстве.

Основные аксиомы и тождества кольца

Аксиомы кольца называют также основными тождествами кольца. Тождество кольца — это равенство, справедливость которого сохраняется при подстановке вместо фигурирующих в нем переменных любых элементов кольца. Основные тождества постулируются, и из них затем могут быть выведены как следствия другие тождества. Рассмотрим некоторые из них.

Напомним, что аддитивная группа кольца коммутативна и в ней определена операция вычитания.

Теорема 2.8. В любом кольце выполняются следующие тождества:

Докажем третью пару тождеств. Рассмотрим первое из них. С учетом доказанного выше имеем

т.е. тождество справедливо. Второе тождество этой пары доказывается аналогично.

Первые два тождества из доказанных в теореме 2.8 выражают свойство, называемое аннулирующим свойством нуля в кольце. Третья же пара тождеств указанной теоремы выражает свойство дистрибутивности операции умножения кольца относительно операции вычитания. Таким образом, производя вычисления в любом кольце, можно раскрывать скобки и менять знаки так же, как и при сложении, вычитании и умножении действительных чисел.

Кольца и делители нуля

При отличных от нуля и приведенные матрицы являются делителями нуля.

Если в кольце имеются делители нуля, то подмножество всех ненулевых элементов кольца не образует группы по умножению уже хотя бы потому, что это подмножество не замкнуто относительно операции умножения, т.е. существуют ненулевые элементы, произведение которых равно нулю.

Кольцо, в котором множество всех ненулевых элементов по умножению образует группу, называют телом, коммутативное тело — полем, а группу ненулевых элементов тела (поля) по умножению — мультипликативной группой этого тела (поля). Согласно определению, поле есть частный случай кольца, в котором операции обладают дополнительными свойствами. Выпишем все свойства, выполнение которых требуется для операций поля. Их еще называют аксиомами поля.

б. Алгебры и есть поля, называемые полями действительных и комплексных чисел соответственно.

в. Примером тела, не являющегося полем, может служить алгебра кватернион.

Итак, мы видим, что известным законам сложения и умножения чисел соответствуют аксиомы поля. Занимаясь числовыми расчетами, мы «работаем в полях», а именно имеем дело преимущественно с полями рациональных и вещественных чисел, иногда «переселяемся» в поле комплексных чисел.

Источник