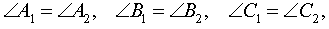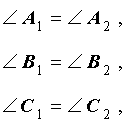Что такое коэффициент подобия треугольников
Что такое коэффициент подобия треугольников
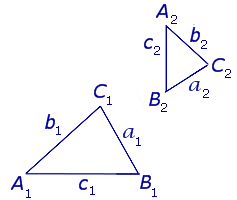
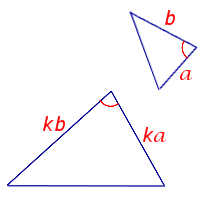
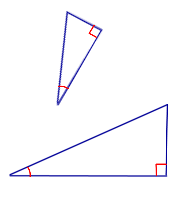
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
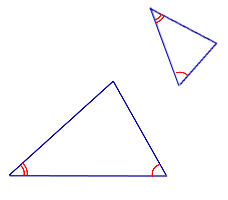
I признак подобия треугольников
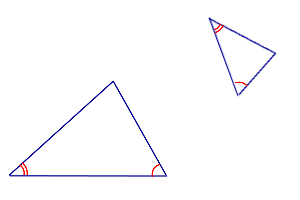
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
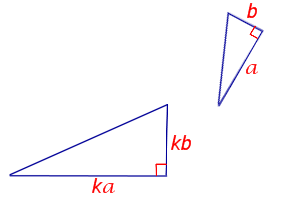
II признак подобия треугольников
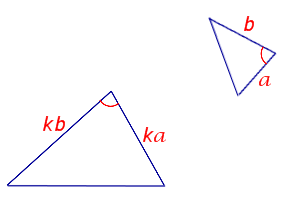
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак подобия треугольников
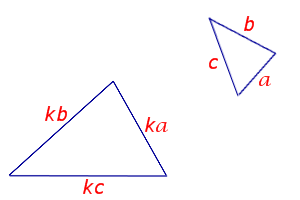
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Подобие треугольников (ЕГЭ — 2022)
Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.
А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?
Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!
Читай эту статью, смотри вебинар по 16 задаче и все поймешь!
Подобие треугольников — коротко о главном
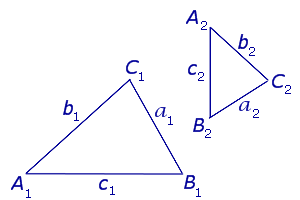
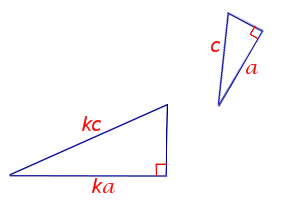
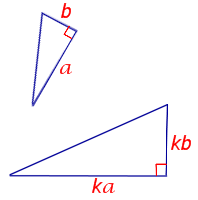
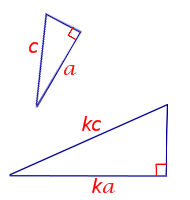
Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия \( \displaystyle k\).
\( \angle A = \angle
Отношение периметров подобных треугольников равно коэффициенту подобия: \( \displaystyle \frac<<
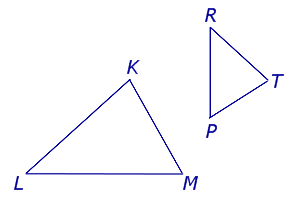
_ _<<_<1>><_<1>>< Отношение площадей подобных треугольников равно квадрату коэффициента подобия: \( \displaystyle \frac<< Признаки подобия треугольников: По двум углам: По одному углу и отношению заключающих его сторон: По отношению трех сторон: Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы: Но что такое подобные треугольники? Вот, например, такой и такой: Похожи эти треугольники? Ты скажешь, конечно же нет! А вот такой и такой? Посмотри внимательно, тоже похожи. А теперь строго математически! Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны. То есть все углы равны и все стороны одного треугольника в \( \displaystyle 5\), или, в \( \displaystyle 7\), или в \( \displaystyle 8,21\) (или и т.д.) больше сторон другого треугольника. Записываются слова «треугольник \( \displaystyle ABC\) подобен треугольнику \( \displaystyle <_<1>><_<1>>< То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы \( \displaystyle k\). \(\angle A = \angle Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон. Помнишь еще, что «\( \displaystyle \sim<\ >\)» обозначает слова «подобен»? Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак. Но есть и еще два. Смотри. Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным? Ну вот, что же хорошего? А то, что тогда… Все элементы одного треугольника ровно в \( \displaystyle 2\) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника. Не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д. Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы. В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение. Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем. Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств). Что такое подобные треугольники? Подобные треугольники определение: На рисунке изображены два подобных треугольника, у них углы соответственно равны, т.е. угол A равен углу A1, угол B равен углу B1, угол C равен углу C1. Сходственные стороны треугольников пропорциональны: здесь k называется коэффициентом подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия: Отношение периметров подобных треугольников: Докажем это утверждение. Пусть имеются два подобных треугольника ABC и A1B1C1. По определению подобных треугольников их сходственные стороны пропорциональны: Периметр треугольника ABC равен сумме длин его трёх сторон: Сумма в скобках в правой части равенства представляет собой периметр треугольника A1B1C1. Разделим обе части равенства на периметр A1B1 + B1C1 + A1C1. Получаем: что и требовалось доказать. Итак, отношение периметров подобных треугольников равно коэффициенту подобия. Для установления факта подобия двух треугольников используют признаки подобия треугольников: Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения. Переобозначим вершины треугольников KLM и TRP так, как показано на рисунке 2. Признак подобия треугольников по двум сторонам и углу между ними Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. Признак подобия треугольников по двум углам Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Признак подобия треугольников по трём сторонам Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны Формулировка признака подобия: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. Формулировка признака подобия: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Формулировка признака подобия: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны Признак подобия прямоугольных треугольников по двум катетам Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Признак подобия прямоугольных треугольников по острому углу Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Признак подобия прямоугольных треугольников по гипотенузе и катету Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Формулировка признака подобия прямоугольных треугольников: Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Формулировка признака подобия прямоугольных треугольников: Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Формулировка признака подобия прямоугольных треугольников: Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника. Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов. I признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. 1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному. 2. Треугольники 3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному. Чтобы не потерять страничку, вы можете сохранить ее у себя: Помогите пожалуйста решить вот такую задачу окруж. пересекает АВ и АС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР если АК=14, а сторона АС в 2 раза больше ВС. Буду очень благодарна. Спасибо Треугольники AKP,ACB подобны по двум углам. очень интересная и полезная информация спасибо Найти отношение периметров подобных треугольников ∆ и ∆, Не понятно, что такое 18 и 6… Найти отношение периметров подобных треугольников ∆ и ∆, Найти отношение периметров подобных треугольников ∆АВС и ∆КМН, Отношение периметров подобных треугольников равно коэффициенту подобия. В прямоугольном треугольнике ABC (LC = 90°) BD — биссектриса. Площади треугольников ABD и BCD относятся как 17:8. Найдите синус угла ABC. Добрый вечер, помогите пожалуйста решить такую задачу: Пусть Почему треугольник LMN равнобедренный? Даша, вы про какую задачу Про эту, конечно же. Которая с трапецией. Не всегда вижу, к чему идет коммент… Помогите решить задачу:Стороны прямоугольника пропорциональны числам 3,4,5.Какими будут стороны подобного ему треугольника с периметром 58,5. Прямоугольник не может быть подобен треугольнику. Видимо, имелось ввиду – Стороны прямоугольного треугольника пропорциональны числам 3,4,5. 2. Треугольники AOD и COB, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –если я найду k мне еще надо найти сторону то как? Вопрос неточен… Нет конкретики. Добрый вечер. Помогите пожалуйста решить эту задачу: в треугольнике АВС угол С – прямой, АС=4. Чему равно расстояние от вершины В до биссектрисы угла А, если расстояние от вершины С до этой биссектрисы равно 2? Пусть Помогите срочно. доказать,что отношение соответствующих биссектрис в подобных треугольниках равно коэффициэнту подобия В параллелограмме ABCD точка К лежит на стороне AD. Отрезок СК пересекает диагональ BD в точке N. Найдите длину диагонали BD, если известно, что ВС=10см, АК=4см, BN=7см. Помог ите решить, там через подобие Треугольники BCN,DKN подобны по двум углам. BN:DN=BC:DK, то есть 7:DN=10:6 Помогите пожалуйста решить задачу. Треугольники АВС И EFG подобны, стороны АВ и EF – сходственные, AB:EF = 1:4. Стороны треугольника АВС равны 5,7,9. Найдите наименьшую сторону треугольника EFG. Стороны треугольника EFG – 20, 28, 36 (каждая сторона в 4 раза больше соответствующей стороны треугольника ABC). __<<_<1>><_<1>><Подобные треугольники — подробнее
Признак подобия треугольников «по двум углам»
Признак подобия треугольников «две пропорциональные стороны и угол между ними»
Признак подобия треугольников «три пропорциональные стороны»
Самый главный «секрет» подобия треугольников
Читать далее…
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Подобные треугольники. Отношение периметров подобных треугольников. Коэффициент подобия
Подобные треугольники определение
Сходственные стороны треугольников
Отношение площадей подобных треугольников
Отношение периметров подобных треугольников
Подобные треугольники. Признаки подобия треугольников
Подобные треугольники
Признаки подобия треугольников
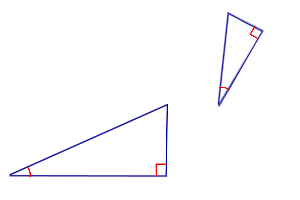
Признаки подобия прямоугольных треугольников
Подобные треугольники
Определение
Признаки подобия треугольников

Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
и
, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
AK:AC=KP:BС, откуда KP=7.
если = 18, = 6.
Помогите)
если = 18см, = 6см.
если ВС = 18, КМ = 6.
Коэффициент подобия в вашем случае, судя по-всему, равен 3.
По хорошему, если BC и KM сходственные стороны, то следовало бы написать вместо ∆KMH – ∆HKM…
Стороны KN и LM трапеции KLMN параллельны, прямые LM и MN – касательные к окружности, описанной около треугольника KLN/
a) Докажите, что треугольники LMN и KLN подобны. Тогда и
Треугольник – равнобедренный.
Но и – равнобедренный, так как вписанный угол
опирается на дугу в
(подумайте, почему…).
Итак, треугольники указанные подобны, так как оба равнобедренные с равными углами при основании (то есть по двум углам).
Потому что по условию MN,ML – касательные к окр. По свойству отрезков касательных.
Пусть – коэффициент подобия. Тогда стороны второго треугольника –
А поскольку его периметр – то
…– перпендикуляры к биссектрисе угла
.
В треугольнике гипотенуза вдвое больше катета
, поэтому
Тогда Стало быть,
В треугольнике также есть угол в 30 градусов. Тогда
Дальше сами…
Думаю, наименьшее из трех чисел выбрать не сложно.