Подробная расшифровка некоторых характеристик акустики

Мощность

Под словом мощность в разговорной речи многие подразумевают «мощь», «силу». Поэтому вполне естественно, что покупатели связывают мощность с громкостью: «Чем больше мощность, тем лучше и громче будут звучать колонки». Однако это распространенное мнение в корне ошибочно! Далеко не всегда колонка мощностью 100 Вт будет играть громче или качественней той, у которой указана мощность «всего» в 50 Вт. Значение мощности, скорее, говорит не о громкости, а о механической надежности акустики. Те же 50 или 100 Вт — это совсем не громкость звука, издаваемого колонкой. Динамические головки сами по себе имеют низкий КПД и преобразуют в звуковые колебания лишь 2-3% мощности подводимого к ним электрического сигнала (к счастью, громкости издаваемого звука вполне хватает для создания звукового сопровождения). Величина, которую указывает производитель в паспорте динамика или системы в целом, говорит лишь о том, что при подведении сигнала указанной мощности динамическая головка или акустическая система не выйдет из строя (вследствие критического разогрева и межвиткового КЗ провода, «закусывания» каркаса катушки, разрыва диффузора, повреждения гибких подвесов системы и т.п.).

Таким образом, мощность акустической системы — это технический параметр, величина которого не имеет прямого отношения к громкости звучания акустики, хотя и связана с ней некоторой зависимостью. Номинальные значения мощности динамических головок, усилительного тракта, акустической системы могут быть разными. Указываются они, скорее, для ориентировки и оптимального сопряжения между компонентами. Например, усилитель значительно меньшей или значительно большей мощности может вывести колонку из строя в максимальных положениях регулятора громкости на обоих усилителях: на первом — благодаря высокому уровню искажений, на втором — благодаря нештатному режиму работы колонки.

Мощность может измеряться различными способами и в различных тестовых условиях. Существуют общепринятые стандарты этих измерений. Рассмотрим подробнее некоторые из них, наиболее часто употребляемые в характеристиках изделий западных фирм:

RMS ( Rated Maximum Sinusoidal power — установленная максимальная синусоидальная мощность). Мощность измеряется подачей синусоидального сигнала частотой 1000 Гц до достижения определенного уровня нелинейных искажений. Обычно в паспорте на изделие пишется так: 15 Вт (RMS). Эта величина говорит, что акустическая система при подведении к ней сигнала мощностью 15 Вт может работать длительное время без механических повреждений динамических головок. Для мультимедийной акустики завышенные по сравнению с Hi-Fi колонками значения мощности в Вт (RMS) получаются вследствие измерения при очень высоких гармонических искажениях, часто до 10%. При таких искажениях слушать звуковое сопровождение практически невозможно из-за сильных хрипов и призвуков в динамической головке и корпусе колонки.

PMPO (Peak Music Power Output — пиковая музыкальная мощность). В данном случае мощность измеряется подачей кратковременного синусоидального сигнала длительностью менее 1 секунды и частотой ниже 250 Гц (обычно 100 Гц). При этом не учитывается уровень нелинейных искажений. Например, мощность колонки равна 500 Вт (PMPO). Этот факт говорит, что акустическая система после воспроизведения кратковременного сигнала низкой частоты не имела механических повреждений динамических головок. В народе единицы измерения мощности Вт (PMPO) называют «китайскими ваттами» из-за того, что величины мощности при такой методике измерения достигают тысячи Ватт! Представьте себе — активные колонки для компьютера потребляют из сети переменного тока электрическую мощность 10 В*А и развивают при этом пиковую музыкальную мощность 1500 Вт (PMPO).

Наравне с западными существуют также советские стандарты на различные виды мощности. Они регламентируются действующими по сей день ГОСТ 16122-87 и ГОСТ 23262-88. Эти стандарты определяют такие понятия, как номинальная, максимальная шумовая, максимальная синусоидальная, максимальная долговременная, максимальная кратковременная мощности. Некоторые из них указываются в паспорте на советскую (и постсоветскую) аппаратуру. В мировой практике эти стандарты, естественно, не используются, поэтому мы не будем на них останавливаться.

Делаем выводы: наиболее важным на практике является значение мощности, указанной в Вт (RMS) при значениях коэффициента гармоник (THD), равного 1% и менее. Однако сравнение изделий даже по этому показателю очень приблизительно и может не иметь ничего общего с реальностью, ведь громкость звука характеризуется уровнем звукового давления. Поэтому информативность показателя «мощность акустической системы» — нулевая.

Чувствительность

Чувствительность — один из параметров, указываемых производителем в характеристике акустических систем. Величина характеризует интенсивность звукового давления, развиваемого колонкой на расстоянии 1 метра при подаче сигнала частотой 1000 Гц и мощностью 1 Вт. Измеряется чувствительность в децибелах (дБ) относительно порога слышимости (нулевой уровень звукового давления равен 2*10^-5 Па). Иногда используется обозначение — уровень характеристической чувствительности (SPL, Sound Pressure Level). При этом для краткости в графе с единицами измерений указывается дБ/Вт*м либо дБ/Вт^1/2*м. При этом важно понимать, что чувствительность не является линейным коэффициентом пропорциональности между уровнем звукового давления, мощностью сигнала и расстоянием до источника. Многие фирмы указывают характеристики чувствительности динамических головок, измеренные при нестандартных условиях.

Чувствительность — характеристика, более важная при проектировании собственных акустических систем. Если вы не осознаете до конца, что означает этот параметр, то при выборе мультимедийной акустики для PC можно не обращать на чувствительность особого внимания (благо указывается она не часто).

Амплитудно-частотная характеристика (АЧХ) в общем случае представляет собой график, показывающий разницу величин амплитуд выходного и входного сигналов во всем диапазоне воспроизводимых частот. АЧХ измеряют подачей синусоидального сигнала неизменной амплитуды при изменении его частоты. В точке на графике, где частота равна 1000 Гц, принято откладывать на вертикальной оси уровень 0 дБ. Идеален вариант, при котором АЧХ представлена прямой линией, но таких характеристик в реальности у акустических систем не бывает. При рассмотрении графика нужно обратить особое внимание на величину неравномерности. Чем больше величина неравномерности, тем больше частотных искажений тембра в звучании.

Нелинейные искажения, коэффициент гармоник

Кг — коэффициент гармонических искажений. Акустическая система представляет собой сложное электроакустическое устройство, которое имеет нелинейную характеристику усиления. Поэтому сигнал по прошествии всего звукового тракта на выходе обязательно будет иметь нелинейные искажения. Одними из самых явных и наиболее простых в измерении являются гармонические искажения.

Коэффициент — величина безразмерная. Указывается либо в процентах, либо в децибелах. Формула пересчета: [дБ] = 20 log ([%]/100). Чем больше величина коэффициента гармоник, тем обычно хуже звучание.

Кг колонок во многом зависит от мощности подаваемого на них сигнала. Поэтому глупо делать заочные выводы или сравнивать колонки только лишь по коэффициенту гармоник, не прибегая к прослушиванию аппаратуры. К тому же для рабочих положений регулятора громкости (обычно это 30..50%) значение производителями не указывается.

Полное электрическое сопротивление, импеданс

Электродинамическая головка имеет определенное сопротивление постоянному току, зависящее от толщины, длины и материала провода в катушке (такое сопротивление еще называют резистивным или реактивным). При подаче музыкального сигнала, который представляет собой переменный ток, сопротивление головки будет меняться в зависимости от частоты сигнала.

Импеданс (impedans) — это полное электрическое сопротивление переменному току, измеренное на частоте 1000 Гц. Обычно импеданс акустических систем равен 4, 6 или 8 Ом.

В целом величина полного электрического сопротивления (импеданс) акустической системы ни о чем, связанном с качеством звучания того или иного изделия, покупателю не скажет. Производителем указывается этот параметр лишь, чтобы сопротивление учитывали при подключении акустической системы к усилителю. Если значение сопротивления колонки ниже, чем рекомендуемое значение нагрузки усилителя, в звучании могут присутствовать искажения или сработает защита от короткого замыкания; если выше, то звук будет значительно тише, нежели с рекомендуемым сопротивлением.

Корпус колонки, акустическое оформление

Одним из важных факторов, влияющих на звучание акустической системы, является акустическое оформление излучающей динамической головки (динамика). При конструировании акустических систем производитель обычно сталкивается с проблемой в выборе акустического оформления. Их насчитывается больше десятка видов.

Акустическое оформление делится на акустически разгруженное и акустически нагруженное. Первое подразумевает оформление, при котором колебание диффузора ограничивается только жесткостью подвеса. При втором колебание диффузора ограничивается помимо жесткости подвеса еще упругостью воздуха и акустическим сопротивлением излучению. Также акустическое оформление делится на системы одинарного и двойного действий. Система одинарного действия характеризуется возбуждением звука, идущего к слушателю, посредством только одной стороны диффузора (излучение другой стороны нейтрализуется акустическим оформлением). Система двойного действия подразумевает использование в формировании звука обеих поверхностей диффузора.

Поскольку на высокочастотные и среднечастотные динамические головки акустическое оформление колонки практически не влияет, мы расскажем о наиболее распространенных вариантах низкочастотного акустического оформления корпуса.

Очень широко применима акустическая схема, получившая название «закрытый ящик». Относится к нагруженному акустическому оформлению. Представляет собой закрытый корпус с выведенным на фронтальную панель диффузором динамика. Достоинства: хорошие показатели АЧХ и импульсная характеристика. Недостатки: низкий КПД, необходимость в мощном усилителе, высокий уровень гармонических искажений.

Но вместо того, чтобы бороться со звуковыми волнами, вызванными колебаниями обратной стороны диффузора, их можно использовать. Наиболее распространенным вариантом из систем двойного действия является фазоинвертор. Представляет собой трубу определенной длины и сечения, вмонтированную в корпус. Длину и сечение фазоинвертора рассчитывают таким образом, что на определенной частоте в нем создается колебание звуковых волн, синфазные с колебаниями, вызванными фронтальной стороной диффузора.

Для сабвуферов широко применяется акустическая схема с общепринятым названием «ящик-резонатор». В отличие от предыдущего примера диффузор динамика не выведен на панель корпуса, а находится внутри, на перегородке. Сам динамик непосредственного участия в формировании спектра низких частот не принимает. Вместо этого диффузор лишь возбуждает звуковые колебания низкой частоты, которые потом многократно увеличиваются по громкости в трубе фазоинвертора, выполяющего роль резонансной камеры. Достоинством этих конструктивных решений является высокий КПД при малых габаритах сабвуфера. Недостатки проявляются в ухудшении фазовых и импульсных характеристик, звучание становится утомляющим.

Оптимальным выбором будут колонки среднего размера с деревянным корпусом, выполненные по закрытой схеме или с фазоинвертором. При выборе сабвуфера следует обратить внимание не на его громкость (по этому параметру даже у недорогих моделей обычно имеется достаточный запас), а на достоверное воспроизведение всего диапазона низких частот. С точки зрения качества звучания, наиболее нежелательны колонки с тонким корпусом или очень маленьких размеров.

Источник

Коэффициент гармоник

Коэффицие́нт нелине́йных искаже́ний (КНИ) — величина для количественной оценки нелинейных искажений, равная отношению среднеквадратичной суммы спектральных компонентов выходного сигнала, отсутствующих в спектре входного сигнала, к среднеквадратичной сумме спектральных компонентов входного сигнала, иногда используется нестандартизованный синоним — клирфактор (заимств. с нем.). КНИ — безразмерная величина, выражается обычно в процентах. Кроме КНИ уровень нелинейных искажений можно выразить с помощью коэффициента гармоник.

Содержание

Измерения

Литература

Ссылки

См. также

Полезное

Смотреть что такое «Коэффициент гармоник» в других словарях:

коэффициент гармоник — Ндп. коэффициент нелинейных искажений клирфактор Коэффициент, характеризующий отличие формы данного периодического сигнала от гармонической, равный отношению среднеквадратического напряжения суммы всех гармоник сигнала, кроме первой, к… … Справочник технического переводчика

коэффициент гармоник — 3.1.3 коэффициент гармоник: Величина, определяемая отношением среднего квадратического напряжения суммы высших гармонических составляющих сигнала модуляции к среднему квадратическому напряжению основной (первой) гармоники этого сигнала. Источник … Словарь-справочник терминов нормативно-технической документации

Коэффициент гармоник — 1. Коэффициент, характеризующий отличие периодического сигнала от гармонической формы, равный отношению среднего квадратического значения напряжения суммы всех гармоник сигнала, кроме первой, к среднему квадратическому значению напряжения первой… … Телекоммуникационный словарь

коэффициент гармоник интегральной микросхемы — коэффициент гармоник Отношение среднеквадратического напряжения суммы всех, кроме первой, гармоник сигнала интегральной микросхемы к среднеквадратическому напряжению суммы всех гармоник. Обозначение Kг Kh [ГОСТ 19480 89] Тематики микросхемы… … Справочник технического переводчика

коэффициент гармоник микрофона телефонного аппарата — Ндп. суммарный коэффициент гармонических искажений микрофона Величина, определяемая отношением суммы эффективных напряжений всех гармоник, кроме первой, к эффективному напряжению первой гармоники электрического сигнала, действующих на зажимах… … Справочник технического переводчика

коэффициент гармоник телефона — Ндп. суммарный коэффициент гармонических искажений телефона Величина, определяемая отношением суммы эффективных напряжений всех гармоник, кроме первой, к эффективному напряжению первой гармоники электрического сигнала, выраженная в процентах,… … Справочник технического переводчика

коэффициент гармоник движения вибростола — 3.14 коэффициент гармоник движения вибростола: Величина, численно характеризующая отклонение от синусоиды закона колебаний вибростола. Источник: МИ 1929 2007: Государственная система обеспечения единства изм … Словарь-справочник терминов нормативно-технической документации

Коэффициент гармоник микрофона телефонного аппарата — 1. Величина, определяемая отношением суммы эффективных напряжений всех гармоник, кроме первой, к эффективному напряжению первой гармоники электрического сигнала, действующих на зажимах микрофона телефонного аппарата, оценивающая нелинейность… … Телекоммуникационный словарь

Источник

Коэффициент нелинейных искажений (КНИ, THD), коэффициент гармонических искажений (КГИ, Kг, THDr) – различные подходы к определению

Коэффициент нелинейных искажений (КНИ, THD)

Коэффициент нелинейных искажений (КНИ) или Total Harmonic Distorsions (THD) – показатель, характеризующий степень отличия формы сигнала от синусоидальной, так же можно сказать это – величина для количественной оценки нелинейных искажений периодического сигнала.

The total harmonic distortion, or THD, of a signal is a measurement of the harmonic distortion present and is defined as the ratio of the RMS of all high harmonic components to the RMS of the fundamental frequency harmonica.

Коэффициент безразмерный, но обычно умножается на 100% для получения значения в %.

Важное замечание:
В силовой электротехнике рассматриваются термины характеризующие нелинейность одного конкретного сигнала (например только сигнала выходного тока). Термины характеризующие нелинейность устройства (усилителя, и т.д.) и включающие в расчёт как входной так и выходной сигналы устройства не используются.

Коэффициент нелинейных искажений сигнала (КНИ, Kн, THD, THDf) – величина, выражающая степень нелинейных искажений сигнала, равна отношению среднеквадратичного значения всех высших гармоник сигнала к напряжению первой гармоники:

Так же в электротехнике используется следующий термин (например Анализаторы сети могут измерять эту величину):

Коэффициент гармонических искажений (КГИ, Kг, THDr) – величина для количественной оценки нелинейных искажений, равная отношению среднеквадратичного значения всех высших гармоник сигнала, к среднеквадратичному значению спектральных компонентов всего сигнала кроме постоянной составляющей:

Соотношения связывающие обе величины:

Современные международные обозначения КНИ (THD)

Приведённые ниже термины повторяют уже рассмотренные в данной статье определения.

1) THDf is the Total Distortion compared to the RMS value of the fundamental frequency value.

THDf is the ratio of the sum of the powers of all harmonic frequency components (except for the fundamental RMS1) to the power of the fundamental frequency component and is calculated as follows:

Remarks:
Total RMS = RMS value of all waveform points (full waveform periods)
RMS0 = RMS value of DC component
RMS1 = RMS value of the fundamental frequency component

Remarks:
Real_i = Real part of the frequency component i
Imag_i = Imaginary part of the frequency component i

2) THDr is the Total Distortion compared to the RMS value of the total waveform.

THDr is the ratio of the sum of the powers of all harmonic frequency components (except for the fundamental RMS1) to the power of all harmonic frequency components and is calculated as follows:

Remarks:
Total RMS = RMS value of all waveform points (full waveform periods)
RMS0 = RMS value of DC component
RMS1 = RMS value of the fundamental frequency component

Remarks:
Real_i = Real part of the frequency component i
Imag_i = Imaginary part of the frequency component i

Прочие определения КНИ (THD), встречающиеся в технической литературе

Существуют другие определения КНИ (THD), например, приведённые ниже. Однако, в силовой электротехнике они не используются.

1) THD:

2) THD+N – общие искажения плюс шум:

Перечень терминов и определений, применяемых ранее в русскоязычных учебниках по радиоэлектронике и электротехнике

Во избежании путаницы ниже представлена терминология, использовавшаяся в русскоязычных учебниках по радиоэлектронике и электротехнике.

Эти термины могут использоваться в настоящее время в радиотехнике, но в силовой электротехнике во избежании путаницы рекомендовано применение международных терминов (см. выше).

В русскоязычной литературе ранее были приняты обозначения и термины:

1) Коэффициент нелинейных искажений (КНИ) или коэффициент искажений или коэффициент гармонических искажений сигнала, равный отношению действующего значениия основной(первой) гармоники к действующему значению всего сигнала (всей функции):

d = Кни = КНИ = A1 / A=I1 / I

d=1 – для синусоидального сигналов
d=

0.99 – для треугольного сигнала
d=0.9 – для прямоугольного сигнала

Положим, что напряжение синусоидально, а ток несинусоидален. В этом случае активная мощность определяется мощностью первой гармоники:

При этом действующее значение тока:

Множитель k_и называется коэффициентом искажения:

Русский термин «коэффициент искажения» эквивалентен зарубежному термину «искаженный коэффициент мощности». Его можно выразить также через THD как показано ниже:

Формула является правильной, но как в отечественной, так и зарубежной литературе, эти термины в силовой электротехнике не используются (или применяются редко). Эту формулу можно получить поставив определение КНИ в формулу определяющую «искажённый коэфф мощности»:

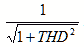2) Коэффициент нелинейных искажений (КНИ) – величина для количественной оценки нелинейных искажений, равная отношению среднеквадратичной суммы всех высших спектральных компонентов сигнала, к среднеквадратичной сумме спектральных компонентов всего сигнала (кроме постоянной составляющей), иногда используется нестандартизованный синоним – клирфактор (заимств. с нем.). КНИ – безразмерная величина, выражается обычно в процентах.

Коэффициент гармонических искажений – величина, выражающая степень нелинейных искажений устройства (усилителя и др.), равная отношению среднеквадратичного напряжения суммы высших гармоник сигнала к напряжению первой гармоники при воздействии на вход устройства синусоидального сигнала.

Коэффициент гармоник (КГ) так же как и КНИ выражается в процентах. Коэффициент гармоник (KГ) связан с КНИ (K Н ) соотношением:

Важное замечание:
Следует признать, что данная терминология долгое время являлась «правильной» для русскоязычной, немецкоязычной литературы, так же именно эти определения продолжают использоваться в некоторых анализаторах сети [10], но в связи с преобладанием обратной терминологии в большинстве современного оборудования (анализаторы сети, ИБП, стабилизаторы, корректоры коэффициента мощности и др.) рекомендуется применение терминов приведенных в самом начале.

Данную терминологию нельзя признать неправильной, но данные и технические характеристики оборудования N-Power указываются в соответствии с европейской и международной терминологией, поэтому рекомендуется применение терминов приведённых в самом начале.

Российский стандарт. Коэффициент нелинейных искажений (КНИ) и качество сетевого электропитания (ГОСТ 13109-97)

Ниже представлены выдержки из ГОСТ 13109-97:

Вычисляют значение коэффициента искажения синусоидальности кривой напряжения Кт в процентах как результат i-го наблюдения по формуле:

где U(1)i — действующее значение междуфазного (фазного) напряжения основной частоты для i-го наблюдения, В, кВ.

При определении данного показателя КЭ допускается:

1) не учитывать гармонические составляющие, значения которых менее 0,1 %;
2) вычислять данный показатель КЭ по формуле

Примечание:
Относительная погрешность определения КUi с использованием формулы (Б.16) вместо формулы (Б.15) численно равна значению отклонения напряжения U(1)i от Uном.

Формула приведенная в данном ГОСТе первой (Б.15) соответствует международному определению термина КНИ / THD (см. начало статьи, см. стандарт EN 62040-3).

Европейский стандарт качества сетевого электропитания (EN 62040-3), и коэффициент нелинейных искажений тока

Коэффициент нелинейных искажений по току в % идентичен базовому определению КНИ, определенному в стандарте EN 62040-3 и рассчитывается как процентное отношение среднеквадратичных значений высших гармоник к базовой (первой) гармоники. См. прилагаемую формулу.

[1] Ф.Е.Евдокимов. Теоретические основы электротехники М., Академия 2004 cтр. 262

[2] Г.И. Атабеков. Основы Теории Цепей с.176, стр. 434

[3] Анализатор сети Fluke 435. Руководство пользователя

[4] Справочник по радиоэлектронным устройствам. В 2-х т. Под ред. Д. П. Линде – М.: Энергия, 1978

[5] Горохов П. К. Толковый словарь по радиоэлектронике. Основные термины – М: Рус. яз., 1993

[6] Коэффициент нелинейных искажений: http://ru.wikipedia.org/

[7] Total Harmonic Distortion: http://en.wikipedia.org/wiki/Total_harmonic_distortion

[8] Total Harmonic Distortion: http://de.wikipedia.org/wiki/THDi http://de.wikipedia.org/wiki/Total_Harmonic_Distortion

[9] П.Шпритек. Справочное руководство по звуковой схемотехнике 3.1.1. Москва Мир 1991

[10] Анализатор сети DMK62 Lovato. Руководство пользователя:
http://www.lovatoelectric.com/RICERCA/ITALIANO/03_ISTRUZIONI/I104IGBFE04_08.PDF

[11] ГОСТ 8.331-99 ГСИ. Измерители коэффициента гармоник. Методы и средства поверки и калибровки.
ГОСТ 8.110-97 ГСИ. Государственная поверочная схема для средств измерения коэффициента гармоник

[13] Анализатор сети HIOKI3197. Руководство пользователя

Современные международные обозначения КНИ(THD)
Приведённые ниже термины повторяют определения приведённые выше.
I

Дополнение1
Замечание: существуют другие определения КНИ(THD) например приведённые ниже но в силовой электротехнике они не используются:
I THD

II THD+N
THD+N обозначает общие искажения плюс шум.

Дополнение2
Внимание!
Во избежании путаницы ниже приведены термины ранее использовавшиеся в русскоязычных учебниках по радио/электротехнике.
Эти термины могут использоваться в настоящее время в радиотехнике но в силовой электротехнике во избежании путаницы рекомендовано применение международных терминов приведённых выше.
В русскоязычной литературе ранее были приняты обозначения и термины:
I
Коэффицие́нт нелине́йных искаже́ний (КНИ)
или Коэффициент искажения(ий)
или Коэффициент гармонических искажений сигнала
равен отношению действующего значениия основной(первой) гармоники к действующему значению всего сигнала (всей функции).
d=Кни=КНИ=A1/A=I1/I
Для синусоиды d=1, для треугольного сигнала d

=0,99, для прямоуг. сигнала d=0,9.
Дополнительная информация:

II
Коэффицие́нт нелине́йных искаже́ний (КНИ) — величина для количественной оценки нелинейных искажений, равная отношению среднеквадратичной суммы всех высших спектральных компонентов сигнала, к среднеквадратичной сумме спектральных компонентов всего сигнала (кроме постоянной составляющей), иногда используется нестандартизованный синоним — клирфактор (заимств. с нем.). КНИ — безразмерная величина, выражается обычно в процентах.

Коэффициент гармонических искажений — величина, выражающая степень нелинейных искажений устройства (усилителя и др.), равная отношению среднеквадратичного напряжения суммы высших гармоник сигнала к напряжению первой гармоники при воздействии на вход устройства синусоидального сигнала.

Коэффициент гармоник так же как и КНИ выражается в процентах. Коэффициент гармоник (KГ) связан с КНИ (KН) соотношением :

Замечание 1: следует признать что данная терминология долгое время являлась «правильной» для русскоязычной, немецкоязычной литературы, так же именно эти определения продолжают использоваться в некоторых анализаторах сети [10], но в связи с преобладанием обратной терминологии в большинстве современного оборудования (анализаторы сети, ИБП, стабилизаторы, корректоры коэфф. мощности и др.) рекомендуется применение терминов приведённых в самом начале.
Эту терминологию нельзя признать неправильной, но данные и технические характеристики оборудования N-Power указываются в соответствии с европейской и международной терминологией, поэтому рекомендуется применение терминов приведённых в самом начале.

Дополнение 3
Выдержки из ГОСТ 13109-97:

Из приведённых в ГОСТ определений видно что вторая формула соответствует определению КНИ (несмотря на то что термин КНИ вообоще отсутствует).

[1] Ф.Е.Евдокимов Теоретические основы электротехники М., Академия 2004 c.262.
[2] Г.И. Атабеков Основы Теории Цепей с.176, 434с.
[3] Анализатор сети Fluke 435 Руководство пользователя
[4] Справочник по радиоэлектронным устройствам: В 2-х т.; Под ред. Д. П. Линде — М.: Энергия, 1978
[5] Горохов П. К. Толковый словарь по радиоэлектронике. Основные термины — М: Рус. яз., 1993
[6] http://ru.wikipedia.org/ Коэффициент нелинейных искажений
[7] http://en.wikipedia.org/wiki/Total_harmonic_distortion
[8] http://de.wikipedia.org/wiki/THDi http://de.wikipedia.org/wiki/Total_Harmonic_Distortion
[9] П.Шпритек Справочное руководство по звуковой схемотехнике 3.1.1, Москва Мир 1991
[10] Анализатор сети DMK62 Lovato Руководство пользователя.
http://www.lovatoelectric.com/RICERCA/ITALIANO/03_ISTRUZIONI/I104IGBFE04_08.PDF
[11] ГОСТ 8.331-99 ГСИ. Измерители коэффициента гармоник. Методы и средства поверки и калибровки
ГОСТ 8.110-97 ГСИ. Государственная поверочная схема для средств измерения коэффициента гармоник
[12] ГОСТ 13109-97
[13] Анализатор сети HIOKI3197 Руководство пользователя

Александр.
SIEL подвердил что все правильно с THD
Можно целиком текст ниже в статью включить+этот стандарт тоже.
Даниил А.
________________________________________
From: Mazza Angelo [mailto: ]
Sent: Wednesday, December 21, 2011 7:33 PM
To: Daniil A.
Cc: ‘Олег Сергеев’; Matoshi Gladiola; Pensini Glauco
Subject: R: SafePower Evo input THD //l2
Dear Mr. Daniil,
the value THDI%, indicated in the manual, is the definition of Total Harmonic Distortion and is exactly equal to the definition expressed by UPS Statement of EN 62040-3, which defines it as the percentage ratio of the rms value of the harmonic content and the rms value of the fundamental component (first harmonic) which expressed by the following relationship:

The values I1, I2, I3, ect….are rms values.

Источник