Что такое кинематическая цепь
iSopromat.ru
Рассмотрим понятия кинематической цепи и механизма:
Кинематическая цепь
Кинематическая цепь – это сочетание звеньев, соединенных в кинематические пары. Имеется определенная классификация кинематических цепей – цепи могут быть простыми и сложными, замкнутыми (закрытыми) и разомкнутыми (открытыми), пространственными и плоскими.
Ранее считалось, что механизм может быть сформирован только на основе замкнутой цепи. Однако с развитием робототехники в качестве механизмов стали широко применяться разомкнутые (открытые) цепи. Поэтому данная классификация в некоторой степени утратила свое первоначальное значение.
Механизм
Механизмом называется кинематическая цепь, имеющая стойку (т.е. звено, принятое за неподвижное), в которой движение одного или нескольких звеньев полностью определяет характер движения остальных звеньев этой цепи.
Другими словами, — это кинематическая цепь, обладающая определенностью движения всех звеньев. Только одним звеньям дается принудительное движение (определенным образом задаются их законы движения, например, подсоединением к двигателю), а другие получают движение от этих звеньев. В итоге механизм можно трактовать как механическую систему тел, предназначенную для преобразования, движения одного или нескольких тел в требуемое движение других тел.
Звенья, законы движения которых заданы, называются входными.
Звенья, законы которых надо определить, называются выходными. Количество входных звеньев определяется числом степеней свободы кинематической цепи, положенной в основу данного механизма.
Понятия входное и выходное (вход и выход) – это кинематическая характеристика. Не надо путать с понятиями – ведущее звено и ведомое звено. Ведущим звеном называется звено, к которому подводится мощность;
ведомое звено – звено, с которого снимается мощность (для выполнения полезной работы).
Таким образом, понятия ведущее и ведомое звено – это силовая (энергетическая) характеристика. Однако в подавляющем большинстве случаев входное звено одновременно является и ведущим, выходное звено – ведомым.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Кинематическая цепь
Связанная система звеньев, образующих между собой кинематические пары, называется кинематической цепью.
Кинематические цепи по характеру относительного движения звеньев разделяются на плоские и пространственные.
Кинематическая цепь называется тоской, если точки звеньев описывают траектории, лежащие в параллельных плоскостях. Кинематическая цепь называется пространственной, если точки ее звеньев описывают неплоские
траектории или траектории, лежащие в пересекающихся плоскостях. Наибольшее распространение на практике имеют плоские кинематические цепи.
По виду звеньев, входящих в кинематические цепи, последние разделяются на простые и сложные.
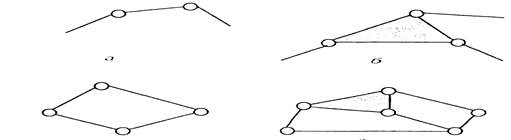
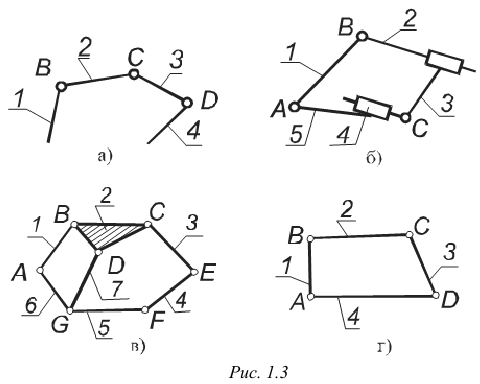
Простой кинематической цепью называется такая цепь, в которой каждое звено участвует в образовании не более двух кинематических пар (рис. 1.3, а).
Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары (рис. 1.3, б).
Все кинематические цепи, кроме того, подразделяются на незамкнутые и замкнутые.
Незамкнутыми кинематическими цепями называют такие цепи, в которых имеются звенья, образующие только одну кинематическую пару (см. рис. 1.3, а, б).
Рис. 1.3
Замкнутыми называются кинематические цепи, в которых каждое звенообразует не менее чем две кинематические пары (рис. 1.3, в, г).
В технике обычно интересует движение звеньев кинематической цепи относительно одного из звеньев, которое является неподвижным и называется стойкой. Если одно звено кинематической цепи сделать неподвижным, то число степеней свободы уменьшится еще на три и относительно неподвижного звена (стойки) будет равно
W = H – 3 = 3(k–1) – 2p1 – p2 (1.2)
где W – число степеней свободы кинематической цени относительно неподвижного звена.
Обозначив к-1= п (количество подвижных звеньев кинематической цепи), окончательно получим выражение для числа степеней свободы кинематической пени относительно неподвижного звена
Число степеней свободы кинематической цепи IV относительно неподвижного звена (стойки) называется степенью подвижности кинематической цепи. Формула (1.3) впервые была получена русским ученым П. Л. Чебышевым и носит его имя. Следует отметить, что эта формула пригодна только для определения степени подвижности плоских кинематических цепей.
Механизмы
Дадим определение механизма на основании понятия о кинематической цепи. Предварительно отметим, что звенья кинематической цепи, законы движения которых являются заданными, называются ведущими, остальные звенья называются ведомыми.
Механизмом называется кинематическая цепь с одним неподвижным звеном (стопкой), в которой при заданном законе движения одного или нескольких ведущих звеньев все остальные (ведомые) звенья движутся вполне определенным образом.
Рассмотрим условия, при которых кинематическая цепь будет механизмом. Известно, что точка на плоскости имеет две степени свободы и для определения ее положения необходимо задать две координаты. В случае твердого тела, имеющего при плоском движении три степени свободы, для однозначного определения его положения необходимо знать три координаты: две координаты точки, выбранной за полюс, и угол поворота некоторого отрезка, соединяющего две точки тела.
Аналогично и для кинематической цепи. Чтобы положения всех звеньев кинематической цепи относительно стойки были вполне определенными, необходимо задать столько параметров, сколько степеней подвижности (степеней свободы относительно стойки) имеет кинематическая цепь. Параметры, которые задаются кинематической цепи, определяются заданным законом движения ведущего звена (или ведущих звеньев). Поэтому, чтобы движения ведомых звеньев кинематической цепи были вполне определенными, необходимо, чтобы количество ведущих звеньев цепи было равно степени подвижности этой цепи. Только в этом случае кинематическая цепь является механизмом.
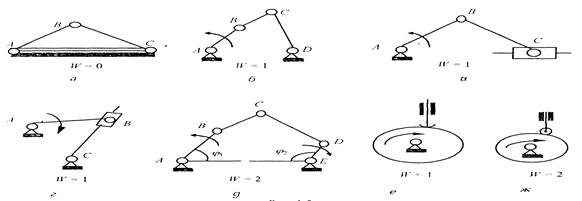
В 1916 г. профессором Петербургского политехнического института Л. В. Ассуром был предложен следующий принцип образования механизмов: любой механизм может быть образован путем непосредственного присоединения («наслоения») сначала к ведущему звену и стойке, а затем и к любым другим звеньям кинематических цепей с нулевой степенью подвижности.
В самом деле, присоединение к ведущему звену кинематических цепей с путевой степенью подвижности (W = 0) не изменит общей степени подвижности механизма.
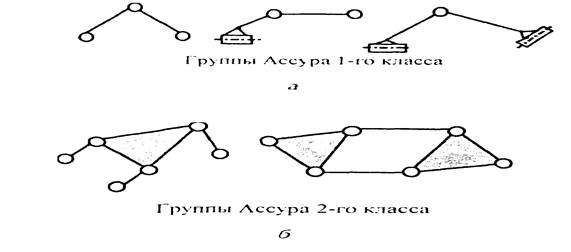
Кинематические цепи, обладающие нулевой степенью подвижности (степенью свободы относительно стойки), называются группами Аcсура. Все разнообразие групп Аcсура можно получить из формулы Чебышева.
Будем полагать, что кинематическая цепь состоит лишь из пар 1-го класса. Тогда для группы Аcсура с нулевой степенью подвижности (W = 0) получим
Так как количество звеньев и кинематических пар может быть только целым числом, то количество звеньев группы Ассура может быть только четным числом. Следовательно, равенству (1.5) могут удовлетворять следующие числа подвижных звеньев п и кинематических пар 1-го класса р1.
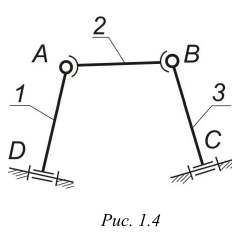
Рис. 1.4
В зависимости от количества звеньев и числа кинематических пар определяется класс группы Ассура. Так, кинематическая цепь с количеством звеньев п = 2 и количеством кинематических пар р1 = 3 является группой Ассура 1-го класса. При п = 2 и р1 = 3 будем иметь группу Ассура 2-го класса и т. д.
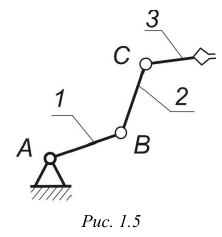
Примеры групп Ассура 1-го и 2-го классов представлены на рис. 1.5, а, 6.
Если присоединить любую группу Ассура к стойке, то получим кинематическую цепь с нулевой степенью подвижности, т. е. ферму (рис. 1.6, а), а если присоединить ее внешними кинематическими парами к ведущему звену и к стойке или к новым звеньям первоначального механизма, то получим новый механизм, степень подвижности которого не изменится (рис. 1.6, б).
Рис 1.5
В соответствии со строением механизмы делятся на классы. Класс механизма зависит от классов групп Ассура, входящих в его состав. Если в состав механизма входят группы Ассура различных классов, то номер класса механизма определяется номером класса наивысшей группы Ассура. На рис. 1.6. б изображен механизм, в состав которого входят группы Ассура 1-го и 2-го классов. Исходя из сказанного выше, данный механизм является механизмом 2-го класса.
Механизмы, не содержащие групп Ассура, а состоящие только из ведущего звена, относятся к механизмам нулевого класса. Такие механизмы встречаются на практике довольно часто. К ним, например, относятся механизмы электродвигателей, генераторов и так далее.
Рассмотренная классификация механизмов не является единственной. Существуют также другие виды классификаций. Широко используется практическая классификация механизмов, которая в общих чертах учитывает основные кинематические свойства и конструктивные особенности механизмов, а в отдельных случаях и функциональное назначение.
В соответствии с практической классификацией механизмы делятся на следующие виды:
а) зубчатые передачи;
б) фрикционные передачи;
в) передачи с гибкой связью;
г) винтовые механизмы;
д) кулачковые механизмы;
е) рычажные механизмы;
ж)механизмы прерывистого действия;
з)электромагнитный механизмы и др.
На рис. 1.7 представлены кинематические схемы механизмов в соответствии с практической классификацией:
фрикционные механизмы: цилиндрический (а) и конический с постоянным передаточным отношением (б), с переменным передаточным отношением (в):
кулачковые механизмы: с поступательно движущимся (г) и качающимся (д) толка гелем;
Кинематические цепи
Кинематические цепи
Кинематическая цепь — это связанная система звеньев, соединенных между собой кинематическими парами. Кинематические цепи можно разделить на плоские и пространственные, простые и сложные, замкнутые и незамкнутые (рис. 1.3). К простым относятся цепи, у которых каждое звено входит не более чем в две кинематические пары (рис. 1.3, а, г); к сложным — цепи, у которых имеются звенья, входящие в три и болей кинематические пары (рис. 1.3, в); к замкнутым — цепи, у которых каждое звено входит, по крайней мере, в две кинематические пары (рис. 1.3, б, г), к незамкнутым — цепи, у которых есть звенья, входящие только в одну кинематическую пару (рис. 1.3, а). Все подвижные звенья плоской кинематической цепи совершают движения, параллельные одной и той же неподвижной плоскости (см. рис. 1.1). В пространственных кинематических цепях точки звеньев описывают пространственные кривые либо жутся по плоским кривым, лежащим в пересекающихся плоскостях (рис. 1.4).
Введя понятие кинематической цепи, можно дать другое определение для механизмов, составленных только из твердых тел. Механизмом называется кинематическая цепь, в которой при одном неподвижном звене (стойке) и заданном движении одного или нескольких звеньев (ведущих) все остальные звенья (ведомые) совершают однозначно определенные движения. Механизмы могут быть образованы как замкнутыми, так и незамкнутыми кинематическими цепями. Примером незамкнутой кинематический цепи может служить механизм элементарного манипулятора (рис. 1.5). Большинство механизмов образовано замкнутыми кинематическими цепями 3 (см. рис. 1.1, 1.4).
При исследовании механизмов используются их условные изображения, составляются структурные, кинематические и другие схемы. Структурные схемы выполняются в виде чертежа, на котором с учетом условных обозначений, установленных ГОСТом, изображают звенья, кинематические пары, указывают стойку и ведущие звенья (см. рис. 1.1). Структурные схемы, выполненные в определенном масштабе, называются кинематическими схемами.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Кинематическая цепь
Кинематическая (или кинетическая) цепь – представляет собой сложную систему подвижно-соединенных звеньев, в которой задействованы кости, суставы, мышцы, сухожилия, нервы, фасции и прочие соединительные ткани.
Основу кинематической цепи составляют кинематические пары, состоящие из двух соседних костных звеньев тела.
Звенья кинематической цепи снабжены мышечными двигателями и обладают определенной:
Все движения, которые совершает человек, подчиняются общим законам механики. Однако количество степеней свободы живого организма, а также работа соединений звеньев кинетической цепи человека, существенно превосходит то, что можно объяснить с точки зрения законов механики, которой объясняется работа неодушевленных механизмов.
Возможности движений в кинематической цепи определяются ее строением (особенностями соединения кинематических пар) и управляющим воздействием мышц.
При этом устройство кинематических пар допускает возможность совершения только определенных и заранее заданных движений.
Такие движения могут:
а) геометрические (постоянные препятствия перемещению в каком-либо направлении, например костное ограничение в суставе);
б) кинематические (ограничение скорости, например мышцей-антагонистом).
Практически все кинематические пары допускают:
В боевых искусствах существует 3 принципа управления кинетической цепью:
Среди кинематических цепей принято выделять три основных вида, это:
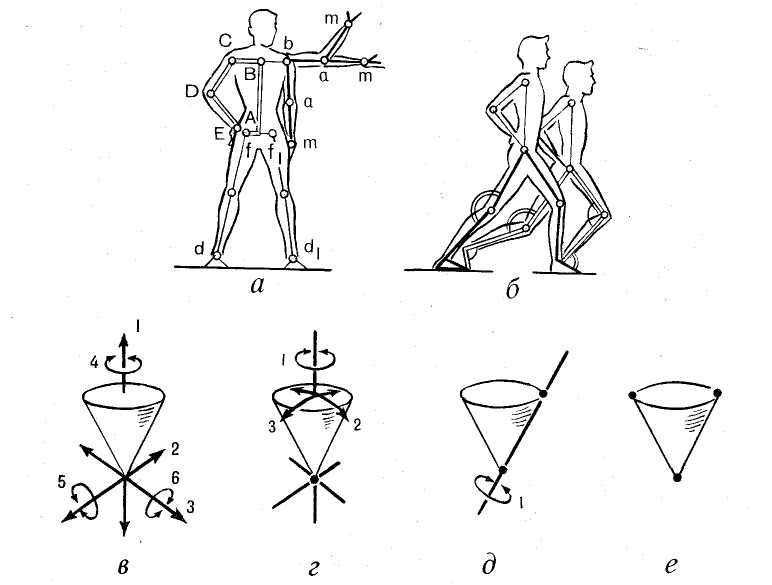
Например, в ударе боксера в нижней части тела задействована трехсуставная кинематическая цепь: стопа – голень – бедро.
Данная кинематическая цепь, передавая поступательное движение туловищу, способствует ускорению вращения таза.
От кинематической цепи – голень – бедро движение передается в следующую трехсуставную цепь: плечо – предплечье – кисть.
Звенья пояса верхней конечности подвижны, например, одна половина пояса может производить движения независимо от другой (правая от левой или левая от правой).
При нанесении ударов усилия передаются от стопы на голень и бедро, затем на таз, туловище к поясу верхней конечности и от него на ударную часть кисти.
Таким образом, начиная с первого момента ударного действия (от толчка стопой) и до заключительного (действия ударной части кисти), сила и скорость как бы нарастают в каждой цепи.
Чем меньше мышцы, тем быстрей они могут сокращаться, но вместе с тем они должны быть достаточно сильными, чтобы поддержать поступательный эффект крупных мышц и ускорит действие, т. е. увеличить силу удара.
В зависимости от направления удара (прямой, боковой, снизу или комбинированный – снизу сбоку, прямой сбоку и т. д.) в активную работу включаются те или иные группы мышц, от качественного действия которых зависят скорость, сила.
Кинематические цепи являются важнейшей составляющей биомеханики.
Знания анатомии, биомеханики и принципов работы кинематических цепей, в частности, очень важны при построении тренировок и достижения поставленных целей при минимальной затрате усилий.
Кинематическая цепь
Содержание
Кинематическая цепь [ править | править код ]
Открытая или незамкнутая кинематическая цепь [ править | править код ]
С точки зрения управления движением наиболее важен случай открытой кинематической цепи, при которой сохраняются возможности опорного энергетического взаимодействия с одновременными активными действиями высокомобильными периферическими звеньями. Степени свободы звеньев открытой кинематической цепи зависят от положения звена относительно опоры. Потенциально наиболее подвижны и энергонасыщенны периферические звенья кинематической цепи, например, рука метателя при броске. Вместе с тем чем больше степеней свободы у звена, тем выше риск двигательной ошибки. Одна из сторон кинематики опорно-двигательный аппарат связана с подвижностью в суставах, которая зависит от ряда факторов. Один из них носит принципиально морфологический характер: шаровидные суставы (плечевой, тазобедренный) допускают трехосное вращение звена, а блоковидные (локтевой) имеют лишь одну степень свободы.
Закрытая или замкнутая кинематическая цепь [ править | править код ]
Такие замкнутые цепи разомкнуть невозможно. Незамкнутые могут замыкаться, причем часто через опору. В сложной пирамиде, составленной несколькими акробатами, образуются даже своего рода «сети» (в плоскости) и «решетки» ( в пространстве) с очень сложной взаимной зависимостью движений звеньев.
В замкнутой или замкнувшейся цепи невозможно изолированное движение, т.е. движение в одиночном сочленении. Так, сгибая и выпрямляя ноги в выпаде, можно убедиться в том, что движение в любом суставе непременно вызывает движения и в других.
Таким образом, движения в незамкнутых цепях характеризуются относительной независимостью звеньев. В замкнутых же, а также замкнувшихся цепях движения одних звеньев влияют на движения даже отдаленных звеньев (помогают или мешают).
В замкнутых цепях возможностей движений меньше, но управление ими точнее, чем в незамкнутых.
Кости, соединенные подвижно, образуют основу биокинематических цепей. Приложенные к ним силы (мышечные тяги и др.) действуют на звенья биокинематической цепи, как на рычаги. Это позволяет передавать действие силы по цепям, а также изменять эффект приложения сил. Таким образом, рычаг как простейший механизм служит для передачи движения и силы на расстояние.
Рычаги [ править | править код ]
Вне зависимости от вида рычага в каждом из них выделяют:
С помощью рычага можно выиграть в силе. Для этого нужно действовать мышечной силой на более длинное плечо. Согласно «золотому правилу механики», выигрывая в силе, одновременно проигрываем в пути и в скорости. Наоборот, если действовать мышечной силой на короткое плечо, то можно выиграть в пути и в скорости за счет проигрыша в силе.
Можно указать еще и на третью причину некоторых потерь в силе мышц. При больших нагрузках напрягаются все мышцы, окружающие сустав. Мышцы-антагонисты, создавая моменты сил, которые направлены противоположно, полезной работы не производят, а энергию затрачивают. Но в конечном счете в этом есть определенный смысл: хотя и возникают потери энергии, сустав во время больших нагрузок получает укрепление напряжением мышц, которые его окружают.
В связи с особенностями приложения мышечных тяг к костным рычагам необходимы весьма значительные напряжения мышц для выполнения не только силовых, но и скоростных движении. При этом следует помнить, что входящие в биокинематические цепи звенья тела образуют системы составных рычагов, в которых «золотое правило» механики проявляется намного сложнее, чем в простых одиночных рычагах.
Амплитуда движений [ править | править код ]
Амплитуда движений в суставах зависит как от морфологии сустава (с пределами, определенными костной конструкцией сустава), так и от податливости мягких тканей, окружающих сустав (суставная сумка, прилегающий мышечно-связочный аппарат). Последняя может изменяться в процессе тренировки и является предметом специальных занятий на гибкость и подвижность в суставах. Одним из аспектов кинематики опорно-двигательный аппарат спортсмена является также аксиальная взаимосвязь движений в суставах пояса верхних конечностей. Так, одновременное сочетание движений на разгибание плеча с супинацией руки (или сгибания плеча с одновременной пронацией) позволяет осуществлять вращательные движения в поясе верхних конечностей без ограничений по углу поворота, что обеспечивает щадящий режим работы сустава. Противоположное сочетание движений (разгибание с пронацией, сгибание с супинацией) вызывает форсированную, предельную деформацию мягких тканей плеча, чреватую травмой. Вместе с тем именно такой режим работы может быть использован для развития подвижности в суставах.