Что такое искомый угол

61. Стереометрия Читать 0 мин.

61.107. Углы

Углы

Классическим заданием с развернутым ответом на стереометрию является задача на нахождение угла. В стереометрии найти угол могут предложить между следующими комбинациями фигур:

Рассмотрим каждую комбинацию, чтобы понять, как искать разные виды углов и какие методы можно применять.

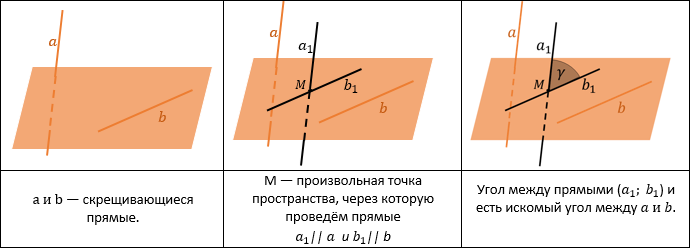
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Угол между скрещивающимися прямыми ― это угол между параллельными им прямыми, лежащими в одной плоскости.

Это значит, что никогда не пересекающиеся прямые в пространстве мы делаем «пересекающимися»: для этого нужно построить пересекающиеся прямые, параллельные данным. Угол между ними будет искомым.

Часто достаточно только к одной из скрещивающихся прямых построить параллельную прямую.

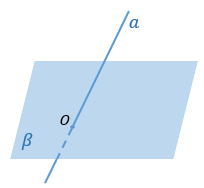
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

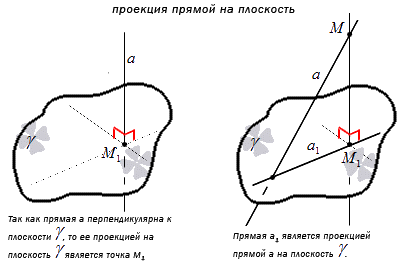
Для того, чтобы найти угол между прямой и плоскостью, нужно сначала получить проекцию этой прямой на плоскость, а потом найти угол.

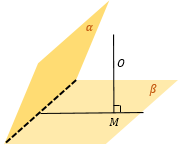
Прямая, пересекающая плоскость β в точке O

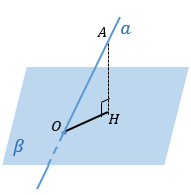
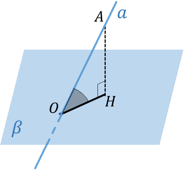
Из произвольной точки А на прямой опустим перпендикуляр AH на плоскость β.

Тогда OH – проекция прямой на плоскость β.

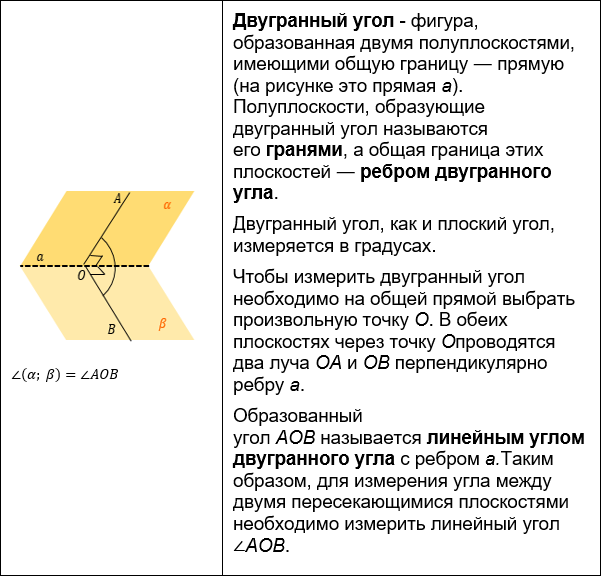
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Для начала вспомним пару определений:

Метод перпендикуляров к линии пересечения.Нахождения угла между плоскостями – одна из самых сложных задач на углы, поэтому тут мы можем воспользоваться несколькими методами.

Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это основной способ нахождения угла между плоскостями.

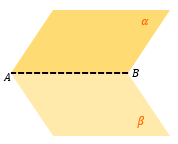
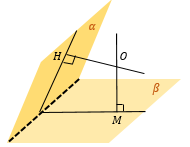
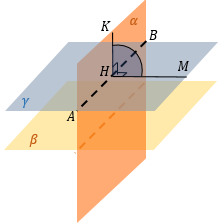
Находим линию пересечения плоскостей α и β – AB.

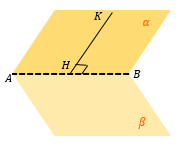
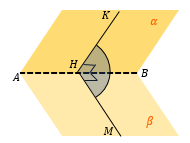
Из «удобной» точки К в плоскости α (это может быть вершина многогранника, середина ребра и т.д.) опускаем перпендикуляр KH на AB.

В точку H опустим перпендикуляр из точки M в плоскости β.

∠ KHM – искомый угол между плоскостями α и β

Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям. Этот способ удобен, если перпендикуляр к плоскости построить удобнее, чем построить перпендикуляры к линии пересечения плоскостей (или перпендикуляр к плоскости уже есть по условию задачи).

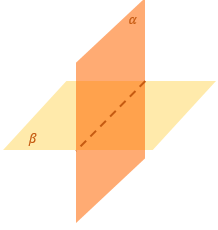
Из произвольной точки O пространства опустим перпендикуляр OM на плоскость β.

Из точки O опустим так же перпендикуляр OH на плоскость α.

Любой из двух смежных углов между OM и OH может считать искомым, но так как угол между плоскостями измеряется от 0 до 90°, то берем острый.

∠ MOK – искомый угол между плоскостями α и β

Угол между плоскостями вычисляется как угол между плоскостями, параллельными данным плоскостям. Этот способ применим, когда угол между данными плоскостями по каким-то причинам искать неудобно, а удобнее найти угол между плоскостями, параллельными данным.

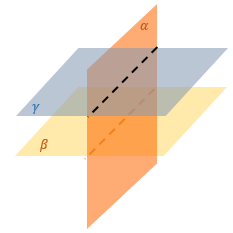
Угол между плоскостями α и β затруднительно искать (например, нет «удобных точек» или тяжело построить взаимные перпендикуляры).

Построим плоскость γ, параллельную β (или в стереометрической фигуре она уже есть)

По методу перпендикуляров к линии пересечения найдем угол между плоскостями α и γ.

∠ MНK – искомый угол между плоскостями α и β

Источник

Угол между прямой и плоскостью: определение, примеры нахождения

Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.

Угол между прямой и плоскостью – определение

Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.

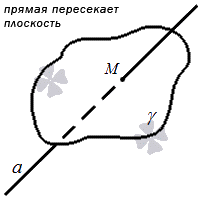
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.

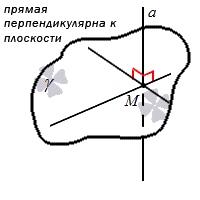
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.

Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.

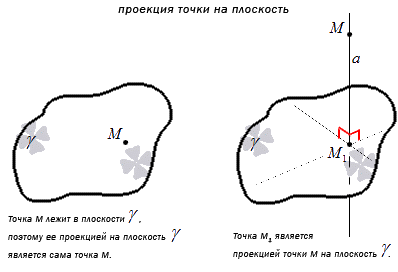
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.

На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью

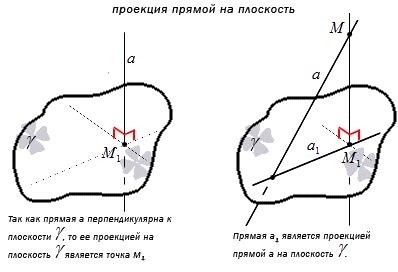
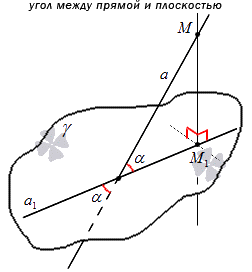
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.

Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.

Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.

Нахождение угла между прямой и плоскостью

Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.

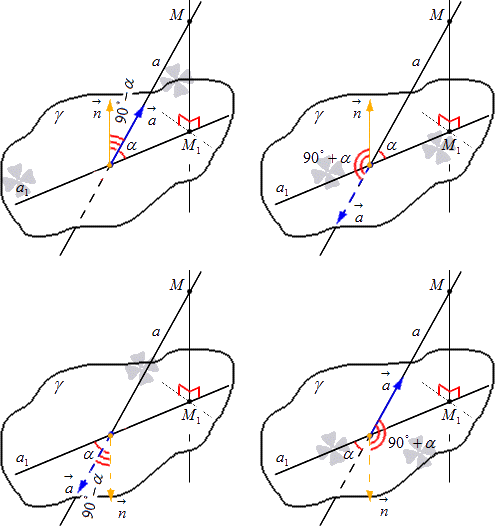
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.

Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.

Отсюда имеем, что косинусы равных углов являются равными, тогда последние равенства записываются в виде системы

Отсюда получим, что синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором заданной плоскости.

Раздел нахождения угла, образованного двумя векторами, выявили, что этот угол принимает значение скалярного произведения векторов и произведения этих длин. Процесс вычисления синуса угла, полученного пересечением прямой и плоскости, выполняется по формуле

Значит, формулой для вычисления угла между прямой и плоскостью с координатами направляющего вектора прямой и нормального вектора плоскости после преобразования получается вида

Выполним решение нескольких подобных примеров для закрепления материала.

Необходимо перейти к вычислению синуса угла между прямой и плоскостью. Для этого необходимо произвести подстановку координат векторов a → и b → в заданную формулу. Получаем выражение вида

Отсюда найдем значение косинуса и значение самого угла. Получим:

Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. получим выражение вида:

Источник

Что такое искомый угол

На этом уроке мы введем понятие угла между прямой и плоскостью, дадим его строгое определение и решим задачи, в которых будет встречаться данный угол.

Наверняка вы слышали такое выражение: «Солнечный луч падает под углом…». (См. Рис. 1.)

Рис. 1. Падает солнечный луч

По сути, здесь идет речь об угле между прямой, частью которой является луч, и «плоскостью» земной поверхности (хотя она, конечно, не совсем плоская).

Мы привыкли, что угол бывает между двумя лучами (см. Рис. 2) или прямыми (см. Рис. 3).

Рис. 2. Угол между лучами

Рис. 3. Угол между прямыми

Как же определить угол между прямой и плоскостью?

Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость.

Чтобы построить проекцию прямой на плоскость, достаточно опустить из любых двух ее точек перпендикуляры на плоскость (спроектировать эти точки), после чего провести через них прямую – это и будет проекция (см. Рис. 4).

Рис. 4. Угол между прямой и плоскостью

Так, проекции всех точек данной прямой будут лежать на одной прямой.

Доказательство

Пусть – точка пересечения прямой и плоскости , и – точки на прямой , и – их проекции на плоскость . Докажем, что , и лежат на одной прямой . (См. Рис. 5.)

Рис. 5. Иллюстрация к доказательству

Заметим, что , так как , . Значит если рассмотреть плоскость , то точки и будут принадлежать ей. Но плоскость пересекает исходную плоскость по некоторой прямой. (См. Рис. 6.)

Рис. 6. Пересечение плоскостей

Значит раз точки , и принадлежат обеим плоскостям, то они лежат на этой прямой, что и требовалось доказать.

То есть мы свели новое определение к углу между прямыми, который мы уже знаем.

Обратите внимание на частую ошибку, которую допускают ученики. Углом между прямой и плоскостью называется угол именно между прямой и ее проекцией, а не между прямой и любой прямой в плоскости. Потому как такие углы могут быть разными.

Рассмотрим куб .

А) Найдите угол между прямой и плоскостью . (См. Рис. 7.)

Рис. 7. Иллюстрация к примеру А

Как мы знаем, искомый угол – это угол между самой прямой и ее проекцией.

Чтобы построить проекцию прямой на плоскость, достаточно взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка . Второй – проекция точки – точка , т. к. боковое ребро куба перпендикулярно плоскости основания. (См. Рис. 8.)

Рис. 8. , следовательно, точка – проекция точки на плоскость

Значит, искомый угол – это угол (см. Рис. 9), а он равен , так как это угол между диагональю и стороной квадрата.

Рис. 9. Искомый угол

Обратите внимание, что если взять вместо другую прямую из плоскости основания, например , то угол будет другим – в данном случае , так как треугольник равносторонний (все стороны – диагонали граней). (См. Рис. 10.)

Рис. 10. Угол в равностороннем треугольнике

Так что угол между прямой и плоскостью – это совсем не угол между прямой и любой прямой в плоскости.

Б) Чему равен угол между и ? (См. Рис. 11.)

Рис. 11. Иллюстрация к примеру Б

Как мы знаем, искомый угол – это угол между самой прямой и ее проекцией.

Чтобы построить проекцию прямой на плоскость, достаточно взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка . Второй – проекция точки – точка , т. к. боковое ребро куба перпендикулярно плоскости основания (см. Рис. 12).

Рис. 12. , следовательно, точка – проекция точки на плоскость

Значит, искомый угол – (см. Рис. 13).

Рис. 13. Искомый угол

Его можно найти из треугольника (см. Рис. 14).

Рис. 14. Треугольник

Треугольник прямоугольный, т. к. , , значит, (см. Рис. 15).

Рис. 15. Выносной рисунок треугольника

Если взять сторону куба за , тогда , и .

Ответ: , .

Вспомните, что расстояние от точки до плоскости – это кратчайший из отрезков, соединяющий исходную точку с точкой плоскости. Подобное верно и для угла: угол между прямой и плоскостью – наименьший из углов между прямой и произвольной прямой в плоскости.

Доказательство

Пусть прямая пересекает плоскость в точке , – проекция на плоскость, а – произвольная прямая в плоскости, проходящая через . Пусть также – перпендикуляр на прямую . (См. Рис. 16.)

Рис. 16. Иллюстрация к доказательству

Тогда несложно видеть, что а . Так как – кратчайшее расстояние от точки до плоскости, то , а значит, .

Найдите угол между боковым ребром правильной четырехугольной пирамиды и ее основанием, если все ее ребра равны . (См. Рис. 17.)

Рис. 17. Иллюстрация к примеру

Пусть – центр основания пирамиды . Как мы знаем, искомый угол – это угол между самой прямой и ее проекцией.

Чтобы построить проекцию прямой на плоскость, достаточно взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка . Второй – проекция точки – точка , т. к. вершина правильной пирамиды проектируется в центр основания. Тогда искомый угол – . (См. Рис. 18.)

Рис. 18. Искомый угол

( – половина диагонали квадрата ), . Значит, , то есть искомый угол .

Ответ: .

Пример

В правильной четырехугольной пирамиде все ребра равны . Найти угол между прямой и плоскостью . (См. Рис. 19.)

Рис. 19. Иллюстрация к условию задачи

Сперва заметим, что, если параллельно перенести прямую , искомый угол не поменяется. Рассмотрим и – середины и соответственно. Тогда можно вместо искать угол между и плоскостью. (См. Рис. 20.)

Рис. 20. Искомый угол – угол между и плоскостью

Далее, заметим, что – проекция точки – попадет на . Действительно, по теореме о трех перпендикулярах, раз и , то есть проекция . А тогда искомый угол – (См. Рис. 21.)

Рис. 21. Искомый угол –

Рассмотрим треугольник . , . Тогда если – середина , то и значит, . (См. Рис. 22.)

Рис. 22. Выносной рисунок

Ответ: .

На этом уроке мы познакомились с таким понятием, как угол между прямой и плоскостью. Выяснили, что этот угол определяется как угол между прямой и ее проекцией на эту плоскость. Также выяснили, что не стоит путать угол между прямой и ее проекцией с углом между прямой и произвольной прямой данной плоскости. Узнали, что угол между прямой и проекцией является наименьшим из углов между прямой и произвольной прямой в плоскости. Решили несколько задач, где наглядно продемонстрировали использование введенного определения.

Список литературы

1. Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов. – 18-е изд. – М.: Просвещение, 2009. – 255 с.

2. Погорелов А.В. Геометрия 10 класс. – 13-е изд. – М.: Просвещение, 2014.

3. Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь по геометрии 10 класс. – 7-е изд. – М.: Просвещение, 2013.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт resolventa.ru (Источник)

2. Интернет-сайт school.xvatit.com (Источник)

3. Интернет-сайт 100ballov.kz (Источник)

Домашнее задание

1. Длина отрезка равна . Он пересекает плоскость в точке . Расстояния от концов отрезка до плоскости соответственно равны и . Найдите острый угол, который образует отрезок с плоскостью.

2. Прямая , проведенная из точки к данной плоскости, равна . Чему равна проекция этой прямой на плоскость, если угол между прямой и данной плоскостью равен ?

3. Под углом к плоскости проведена прямая. Найдите , если известно, что проекция прямой вдвое меньше самой прямой.

Источник