Что такое интересные суждения
Значение слова «суждение»
1. Мнение о чем-л., взгляд на что-л. Суждения об искусстве. □ Дед не терпит, когда при нем высказывают свои суждения: сыновья должны беспрекословно выполнять его приказания. Гладков, Повесть о детстве. || Заключение, решение. Я решаюсь вынести этот маленький спор на ваше суждение. Леонов, Непримиримость.
2. Лог. Мысль, в которой утверждается или отрицается что-л. относительно предмета или явления, например: «все люди — братья», «железо ковко».
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Виды суждений и отношения между ними изучаются в философской логике.
В математической логике суждениям соответствуют высказывания.
СУЖДЕ’НИЕ, я, ср. 1. только ед. Действие по глаг. судить в 1 знач., обсуждение (книжн. устар.). С общего сужденья приговорили. Крылов. Длительное с. о деле. 2. Мнение, заключение. Не смею моего сужденья произнесть. Грибоедов. В мои лета́ не должно сметь свое суждение иметь. Грибоедов. 3. В логике — форма мышления, представляющая собою сочетание понятий, из к-рых одно (предикат) определяет и раскрывает
содержание другого (субъекта; филос.).
Настало время, говорит Энгельс, когда человеческий мозг развился настолько, что мог высказать суждение: трение есть источник теплоты.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
сужде́ние
1. мнение, высказывание о ком-, чём-либо ◆ Сверхценные идеи, будучи эмоционально весьма насыщенными, занимают в психике центральное место и мешают человеку быть в достаточной мере беспристрастным и объективным в своих суждениях. И.Я. Завилянский, В.М. Блейхер, «Психиатрический диагноз», 1979 г.
2. в логике форма мышления, представляющая собою сочетание понятий, одно из которых — субъект — определяется и раскрывается через другое — предикат
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: заочный — это что-то нейтральное, положительное или отрицательное?
Суждение
Суждение — форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами. Виды суждений и отношения между ними изучаются в философской логике.
Содержание
Простые и сложные суждения
Простые суждения — суждения, составными частями которых являются понятия. Простое суждение можно разложить только на понятия.
Сложные суждения — суждения, составными частями которых являются простые суждения или их сочетания. Сложное суждение может рассматриваться как образование из нескольких исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (связками). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения.
Состав простого суждения
Простое (атрибутивное) суждение — это суждение о принадлежности предметам свойств (атрибутов), а также суждения об отсутствии у предметов каких-либо свойств. В атрибутивном суждении могут быть выделены термины суждения — субъект, предикат, связка, квантор.
Состав сложного суждения
Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит, и любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различают конъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения.
Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают:
Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как 
или 
. В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции (эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как 
.
Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как 
(у разных математиков по-разному, хотя математический знак тождества всё-таки 
).
Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a
b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b).
Классификация простых суждений
По качеству
По объёму
По отношению
По отношению между подлежащим и сказуемым
Субъект и предикат суждения могут быть распределены (индекс «+») или не распределены (индекс «-»).
Суждения А (обще-утвердительные суждения) Распределяет свое подлежащее (S), но не распределяет свое сказуемое (P)
Объем подлежащего (S) меньше объема сказуемого (Р)
Объемы подлежащего и сказуемого совпадают
Суждения Е (обще-отрицательные суждения) Распределяет как подлежащее (S), так и сказуемое (P)
В этом суждении мы отрицаем всякое совпадение между подлежащим и сказуемым
Суждения I (частно-утвердительные суждения) Ни подлежащие (S), ни сказуемые (P) не распределены
Часть класса подлежащего входит в класс сказуемого.
Суждения О (частно-отрицательные суждения) Распределяет свое сказуемое (Р), но не распределяет свое подлежащее (S) В этих суждениях мы обращаем внимание на то, что есть несовпадающего между ними (заштрихованная область)
таблица распределения подлежащего и сказуемого
| Подлежащее (S) | Сказуемое (P) | ||
|---|---|---|---|
| о-у | А | распределено | нераспределено |
| о-о | Е | распределено | распределено |
| ч-у | I | нераспределено | нераспределено |
| ч-о | О | нераспределено | распределено |
Другие
1) S есть или А, или В, или С
2) или А, или В, или С есть Р когда в суждении остается место неопределенности
Если А есть В, то С есть D или Е есть F
если есть А, то есть а, или b, или с Прим: « Если кто желает получить высшее образование, то он должен учиться или в университете, или в институте, или в академии»
Модальность суждений
Модальные понятия, или модальности — понятия, выражающие контекстную рамку суждения: время суждения, место суждения, знание о суждении, отношение говорящего к суждению.
В зависимости от модальности выделяются следующие основные виды суждений:
2.1. Что такое суждение?
2.1. Что такое суждение?
Суждение – это вторая после понятия форма мышления. Суждением называется форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: Все сосны являются деревьями; Некоторые люди – это спортсмены; Ни один кит – не рыба; Некоторые животные не являются хищниками и т. п. Суждение также называется высказыванием.
Рассмотрим несколько важных свойств суждения, которые также являются его отличиями от понятия.
1. Любое суждение состоит из понятий, связанных между собой. Например, если связать между собой понятия карась и рыба, то может получиться суждение: Все караси являются рыбами или Некоторые рыбы являются карасями.
2. Любое суждение выражается в форме предложения (вспомним, понятие выражается в слове или словосочетании). Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. Суждение – это форма мышления, в которой что-либо утверждается или отрицается. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда представляет какое-то утверждение или отрицание, в силу чего суждение выражается в форме повествовательного предложения. Тем не менее, есть такие вопросительные и восклицательные предложения, которые только по форме являются вопросами и восклицаниями, а по смыслу что-то утверждают или отрицают. Они называются риторическими. Например, известное высказывание: И какой же русский не любит быстрой езды? представляет собой риторическое вопросительное предложение (или риторический вопрос), т. к. в нем в форме вопроса утверждается, что всякий русский любит быструю езду. Такой вопрос, конечно же, выражает собой суждение. То же самое можно сказать о риторических восклицаниях. Например, в высказывании: Попробуй найти черную кошку в темной комнате, если ее там нет! в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение. Понятно, что не риторический, а настоящий вопрос, например: Как тебя зовут? не выражает собой суждение, точно так же, как не выражает его настоящее, а не риторическое восклицание, например: Прощай, свободная стихия! Приведем еще несколько примеров.
а) Неужели ты не знал, что Земля вращается вокруг Солнца? (риторический вопрос – является суждением).
б) Прощай, немытая Россия! (восклицание – суждением не является).
в) Кто написал философский трактат «Критика чистого разума»? (вопрос – суждением не является).
г) Логика появилась примерно в V в. до н. э. в Древней Греции (повествование – является суждением).
д) первый президент Америки (понятие – суждением не является).
е) Разворачивайтесь в марше! (восклицание – суждением не является).
3. Любое суждение является истинным или ложным. Если суждение соответствует действительности или реальности, оно истинное, а если не соответствует, – ложное. Например, суждение: Все розы – это цветы является истинным, а суждение: Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа – истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета – ложное и т. п. Но разве понятия Змей Горыныч или Кащей Бессмертный, или вечный двигатель не ложные? Нет, не ложные, эти понятия являются нулевыми или пустыми, но не истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает собой какой-либо объект, – и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, в силу чего она применима только к суждениям, но не к понятиям. Поскольку любое суждение принимает одно из двух значений – истины или лжи, – то аристотелевская формальная логика также часто называется двузначной логикой.
4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом. О простых и сложных суждениях речь пойдет далее.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
А. СУЖДЕНИЕ
А. СУЖДЕНИЕ Суждение — это мысль, в которой утверждается наличие или отсутствие каких-либо ситуаций или связей между ситуациями. В языке суждение, как правило, выражается повествовательным предложением и может оцениваться в качестве истинного или ложного.Примеры
Глава 2 Суждение
Глава 2 Суждение 2.1. Что такое суждение? Суждение – это вторая после понятия форма мышления. Суждением называется форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: Все сосны являются деревьями; Некоторые люди – это спортсмены; Ни один кит
2.1. Что такое суждение?
2.1. Что такое суждение? Суждение – это вторая после понятия форма мышления. Суждением называется форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: Все сосны являются деревьями; Некоторые люди – это спортсмены; Ни один кит – не рыба;
3. Суждение
3. Суждение Понятий, как вообще всякие мысли, не существуют изолированно друг от друга, они всегда взаимосвязаны. Связь эта может быть различной: в сочетании понятий «ель — хвойное дерево» понятие «ель» включается в понятие «хвойное дерево»; в сочетании «кит не рыба»
1. Суждение и предложение
1. Суждение и предложение Суждения обычно выражаются в определенных языковых предложениях. В языкознании различают, вообще говоря, четыре типа предложений, а именно: 1. повествовательные, или утвердительные предложения, 2. вопросительные предложения, 3. желательные
Понятие и суждение
§ 1. СУЖДЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. СУЖДЕНИЕ И ПРЕДЛОЖЕНИЕ
§ 1. СУЖДЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. СУЖДЕНИЕ И ПРЕДЛОЖЕНИЕ Суждение как форма мышленияПознавая окружающий мир, человек раскрывает связи между предметами и их признаками, устанавливает отношения между предметами, утверждает или отрицает факт существования предмета. Эти
А. СУЖДЕНИЕ
А. СУЖДЕНИЕ Суждение — это мысль, в которой утверждается наличие или отсутствие каких-либо ситуаций или связей между ситуациями. В языке суждение, как правило, выражается повествовательным предложением и может оцениваться в качестве истинного или ложного.Примеры
2. Суждение и предложение
2. Суждение и предложение Суждение и назначение предложений. Подобно понятию, суждение выражается посредством языка. Но, как более сложная форма мышления, она облекается и в более сложную языковую форму. Если материальной оболочкой понятия служит слово (или
(β) Моральное суждение
(?) Моральное суждение Но это суждение имеет в то же время другую сторону, начинающую разрешение имеющейся здесь противоположности. — Сознание всеобщего относится к злому сознанию не как то, что действительно и совершает поступки (ведь, напротив, злое сознание есть то,
23. Суждение
23. Суждение Суждение – это форма мышления, в которой утверждается или отрицается что-либо об окружающем мире, предметах, явлениях, а также отношениях и связях между ними.Суждения выражаются в форме высказывания относительно определенного предмета. Например, суждениями
II. Суждение
II. Суждение § 11Суждение есть выражение некоторого предмета в различных моментах понятия. Суждение содержит: a) предмет в определении единичности как субъект; b) его определение всеобщности, или его предикат, причем однако же субъект может относиться к предикату и как
II. Суждение
II. Суждение § 58Суждение есть отделение субъекта от его определения, или же особенности, и соотнесение его с этой особенностью, представляющей собой его предикат. Субъект и предикат относятся друг к другу либо как единичное и особенное, либо как единичное и всеобщее, либо
1. ЧТО ТАКОЕ МАТЕРИЯ? ЧТО ТАКОЕ ОПЫТ?
1. ЧТО ТАКОЕ МАТЕРИЯ? ЧТО ТАКОЕ ОПЫТ? С первым из этих вопросов постоянно пристают идеалисты, агностики, и в том числе махисты, к материалистам; со вторым — материалисты к махистам. Попытаемся разобраться, в чем тут дело.Авенариус говорит по вопросу о материи:«Внутри
II. Суждение
II. Суждение Познавательная деятельность приводит всегда к истине или к лжи. В какой же форме выражается истина или ложь? В форме суждения, отвечает на этот вопрос логика. Но если так, то это значит, что представления, понятия и даже умозаключения, служа выразителями истины
Урок 4. Суждения и высказывания. Введение в силлогистику
В прошлых уроках рассказывалось о том, как правильно работать с понятиями и определениями. Хотя операции над ними очень важны и встречаются повсеместно, сами по себе они ещё не составляют рассуждений. В этом уроке мы как раз приблизимся к теме того, как правильно рассуждать. Мы будем рассматривать рассуждения на примере силлогистики. Силлогистика – это самая древняя логическая система. Она была изобретена древнегреческим философом Аристотелем в IVвеке до н.э. До сих пор она остаётся одной из самых понятных, приближенных к естественному языку и лёгких для изучения логических систем. Одно из главных её достоинств – возможность применения в повседневных ситуациях без особых усилий.
Содержание:
Суждения и высказывания
Что такое рассуждение? Можно было бы сказать: вывод, умозаключение, размышление, доказательство и т.д. Всё это верно, но, пожалуй, самым очевидным ответом было бы: рассуждение – это последовательность суждений, которые в идеале должны быть связаны между собой согласно правилам логики. Поэтому обучение правильному рассуждению нужно начинать с того, что такое суждения и как ими корректно пользоваться.
Суждение – это мысль об утверждении или отрицании наличия некоторой ситуации в мире.
В естественном языке суждения передаются с помощью повествовательных предложений, или высказываний. Примеры суждений, выраженных в высказываниях: «Пришла осень», «Катя не знает английского языка», «Я люблю читать», «Трава зелёная, а небо голубое». Одно и то же суждение может быть выражено с помощь разных высказываний, в частности: «Небо голубое» и «The sky is blue» – разные высказывания, но суждение они выражают одно и то же, так как они передают одну и ту же мысль. Точно также высказывания «Никто не покидал дома» и «Все оставались дома» разные, но они передают одно суждение.
Поскольку высказывания посредством суждений фиксируют какое-то положение дел в мире, в отличие от понятий и определений, мы можем оценивать их с точки зрения их истинности и ложности. Так высказывание «Бил Гейтс основал компанию “Microsoft”» – истинное, а высказывание «Апельсины фиолетовые» – ложное.
Если вспомнить треугольник Фреге, то высказывание будет находиться на вершине, обозначающей знак, суждение будет составлять его смысл, а истина и ложь – значение.
Существует множество типов суждений и, соответственно, высказываний. Разные логические системы концентрируются на их разных аспектах. Силлогистика работает с так называемыми категорическими атрибутивными высказываниями. Категорические высказывания противопоставляются гипотетическим. Гипотетические высказывания говорят о возможности наличия или отсутствия какой-то ситуации в мире: «Возможно, пойдёт дождь». Категорические высказывания безапелляционно утверждают о том, что какая-то ситуация имеется или не имеется: «Пошёл дождь». Термин «атрибутивный» означает, что эти высказывания говорят о наличии либо отсутствии у предмета или класса предметов некоторого свойства. Примеры категорических атрибутивных высказываний: «Моя машина синего цвета», «Парк около нашего дома большой», «Никто не любит рыбий жир», «Некоторые люди считают, что они самые умные». Хотя на первый взгляд может показаться, что из-за концентрации именно на категорических атрибутивных высказываниях, применение силлогистики ограничено, это не так. Огромный пласт рассуждений не выходит за рамки подобных высказываний, а потому знания силлогистики оказывается достаточно для того, чтобы научиться размышлять логично и не давать ввести себя в заблуждение.
Состав и виды категорических атрибутивных высказываний
Категорические атрибутивные высказывания состоят из терминов, предицирующих связок и кванторов.
Термины делятся на субъект и предикат.
Предицирующие связки, как, возможно, вы помните из первого урока, это связки «есть» и «не есть». В естественном языке они могут выражаться с помощью разных слов и конструкций: «есть», «являться», «суть», «это», «выступать», знака тире, глаголов, либо вообще опускаться.
Кванторы – это слова, указывающие на количественные характеристики субъекта. Существует два вида кванторов: квантор общности («все», «каждый», «любой», «ни один», «никто») и квантор существования («некоторые», «не все», «какой-либо», «многие»). Также как и предицирующие связки, кванторы в естественной речи могут опускаться. Мы можем сказать: «Люди равны перед законом», подразумевая, что «Все люди равны перед законом»; или «Дети любят сладкое» – подразумевая, что «Многие дети любят сладкое». Зачастую лучше всего уточнить у вашего собеседника, какой именно квантор он имеет в виду, так как это будет сказываться на условиях истинности его высказываний.
Давайте разберём следующее высказывание: «Кошки мурлычут, когда им приятно». «Кошки» – это субъект, «существа, мурлычущие, когда им приятно» – это предикат. Также здесь присутствует невидимая связка «есть», которая соединяет субъект с предикатом, и невидимый квантор общности «все». Так, если записать это высказывание в соответствии с его логической формой, то получим: «Все кошки есть существа, которые мурлычут, когда им приятно». Благодаря этому примеру становится ясно, что прежде чем определять, истинно высказывание или ложно, нужно выявить его логическую форму и преобразовать исходное высказывание так, чтобы все четыре элемента (квантор, субъект, связка, предикат) были на своих местах.
В зависимости от свойств логических и нелогических терминов, входящих в состав категорических атрибутивных высказываний, их можно разделить на несколько видов.
Если мы скомбинируем эти виды между собой, то получается, что всего существует шесть видов категорических атрибутивных высказываний:
Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике
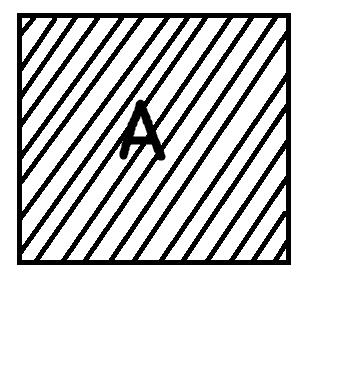
Следует начать с того, что традиционная силлогистика накладывает два ограничения на используемые термины, а именно: они должны быть непусты и неуниверсальны, то есть если под термин не подпадает ни один объект из универсума рассмотрения или, наоборот, подпадают все объекты универсума, то они не могут быть предметом рассмотрения. Посмотрим на рисунки:
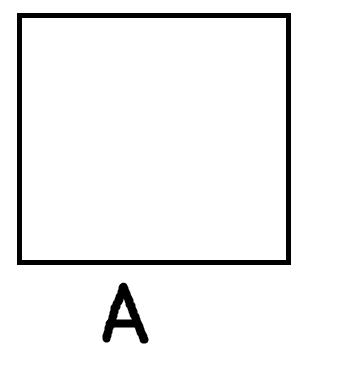
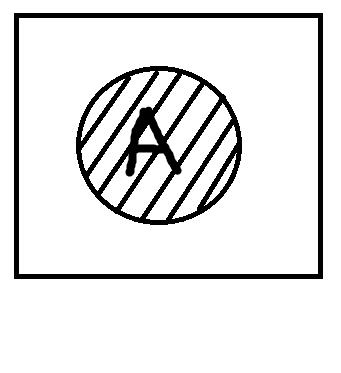
Первый рисунок изображает ситуацию, когда термин А пуст, поэтому весь квадратик (универсум рассмотрения) остался белым. Второй рисунок показывает случай, когда объём термина А совпадает с объёмом универсума рассмотрения, поэтому весь квадрат заштрихован. Последний рисунок репрезентирует термин А, который является непустым и в то же время неуниверсальным. Заштрихованая область соотвествует объёму А. Традиционная силлогистика работает только с терминами, которые соотвествуют третьему рисунку. Такое условие ставится для того, чтобы исключить из рассмотрения высказывания, которые невозможно оценить как истинные либо ложные. Возьмём высказывание: «Все дети Ивана лысые». Вроде бы с высказыванием всё впорядке, однако представьте, что у Ивана нет детей. Мы не можем в данном случае просто сказать, что высказывание ложное. Если назвать его ложным, то тем самым мы подразумеваем, что не все дети Ивана лысые, а это не так. В то же время мы не можем сказать, что оно истинное. Выход из этого затруднительного положения состоит как раз в том, чтобы указать на пустоту термина «дети Ивана». Поскольку у Ивана нет детей, этот термин пуст, и мы не можем построить с ним корректное высказывание.
Непустота и неуниверсальность термина будут определяться не только контекстом, но и выбранным универсумом рассмотрения. Если наш квадратик представляет собой универсум живых существ или материально существующих предметов, то, конечно, такие термины как «русалка», «хоббит», «дракон» и т.п. окажутся пустыми, и мы не сможем их рассматривать. Однако, если универсум рассмотрения – это мифологические или сказочные существа, то все эти термины перестают быть пустыми. То же самое верно и для универсальности. Термин «люди» может рассматриваться как универсальный, что исключает его из области традиционной силлогистики. Однако если мы хотим сказать «Сократ – человек», то в качестве универсума рассмотрения вполне можно взять живых существ. На универсуме живых существ, термин «люди» уже не будет универсальным.
Кроме того, нужно помнить, что субъект и предикат должны задаваться на одном и том же универсуме рассмотрения.
Теперь посмотрим, при каких условиях разные типы категориальных атрибутивных высказываний будут истинными. Для этого советуем ещё раз заглянуть в урок, посвящённый отношениям между понятиями. По большому счёту, субъект и предикат – это термины, представляющие некоторые понятия. Соответственно, если соединить эти понятия в одном предложении с помощью предицирующих связок и кванторов, то, чтобы узнать будут эти предложения истинными или ложными, достаточно посмотреть на диаграммы, иллюстрирующие отношения между этими двумя понятиями. Итак, преступим.
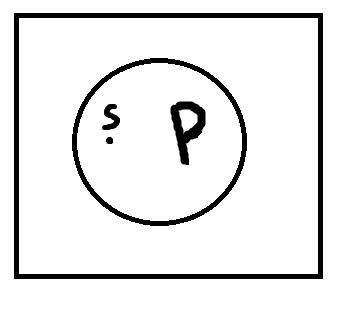
Единичноутвердительные высказывания формы «s есть P» истинны, только если термины s и P находятся в следующем отношении:
Другими словами, единичноутвердительные высказывания истинны, если точка, представляющая собой имя s, находится внутри кружочка, изображающего объём термина P. Например, возьмём высказывание «Лев Толстой проповедовал вегетарианство». «Лев Толстой» – это субъект, имя s. «Человек, проповедующий вегетарианство» – это предикат, термин P. Это высказывание истинно, так как точка s будет входить в объём термина P. Если же взять высказывание «Николай Гоголь – это великий русский композитор», то точка s, представляющая имя («Николай Гоголь»), не будет входить в объём термина P («великие русские композиторы»). Поэтому это высказывание ложно.
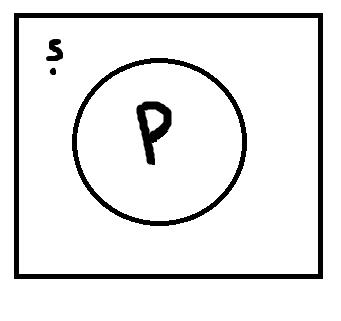
Единичноотрицательные высказывания, имеющие форму «s не есть P» истинны, если термины s и P находятся в следующем отношении:
Как видно из рисунка, здесь имеет место ситуация, прямо противоположная условиям истинности единичноутвердительных высказываний. Если точка, представляющая имя s, находится вне объёма термина P, то высказывание истинно. В обратном случае, оно ложно. Пример истинного единичноотрицательного высказывания: «Александр Пушкин никогда не был во Франции». Ложным единичноотрицательным высказыванием будет: «Иван Бунин не получил Нобелевскую премию по литературе».
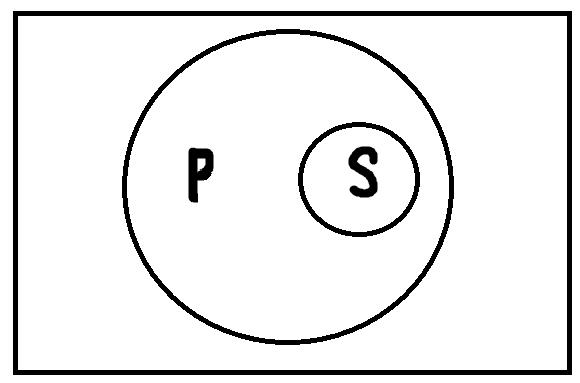
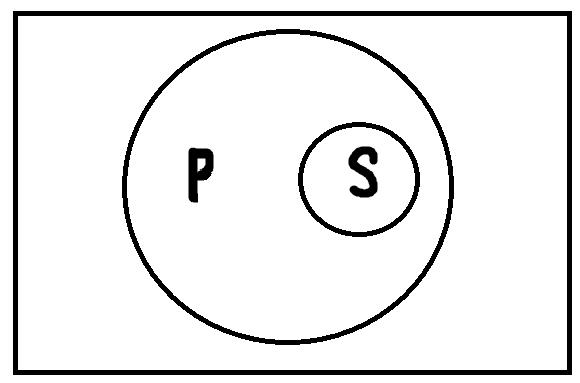
Общеутвердительные высказывания формы «Все S есть P» истинны, если термины S и P находятся в одном из следующих отношений:
Первый рисунок изображает отношение равнообъёмности, второй – обратного подчинения. Если объёмы двух терминов совпадают (S и P делят один кружочек) или объём термина S полностью входит в объём термина P (кружочек S полностью включается в P), то общеутвердительное высказывание истинно. Если термины S и P находятся в каком-либо другом отношении, то общеутвердительные высказывания не могут быть истинными. В качестве иллюстрации истинных высказываний можно привести: «Все хвойные растения имеют шишки», «Все киты – это млекопитающие». Пример ложных высказываний: «Все политики – обманщики», «Все девушки мечтают выйти замуж за миллионера». В этих примерах термины, обозначающие субъект и предикат, не находятся ни в одном из указанных выше отношений.
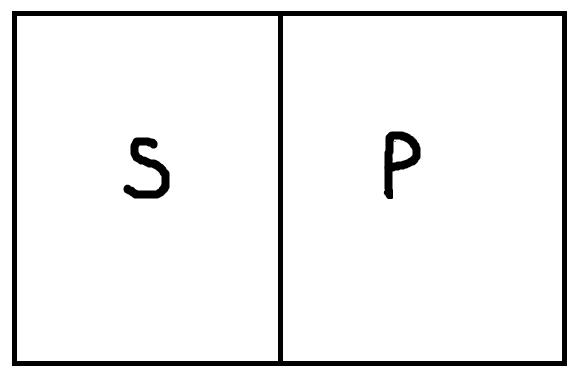
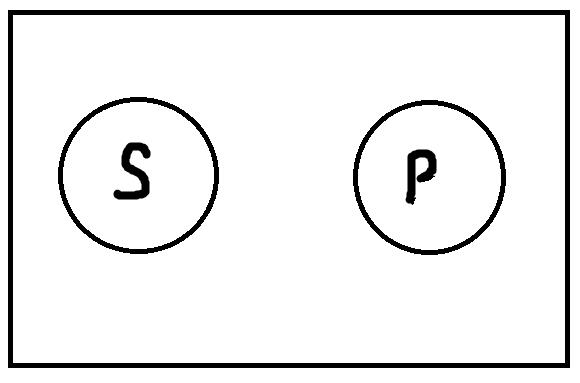
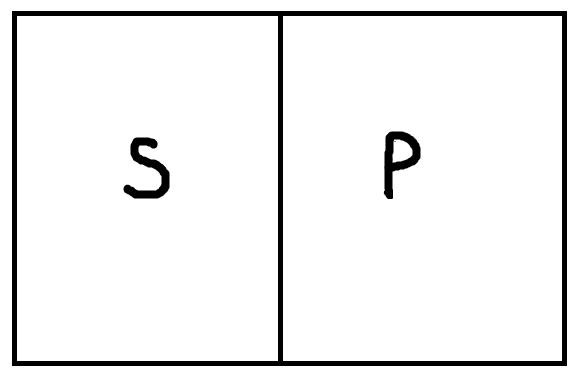
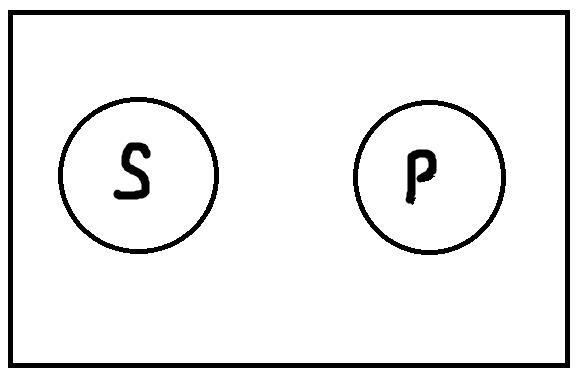
Общеотрицательные высказывания, имеющие форму «Ни один S не есть P» истинны, только если термины S и P находятся в следующих отношениях:
На первом рисунке представлено отношение противоречия, а на втором – соподчинения. Как видно, у S и P нет общих элементов, их объёмы не пересекаются. К примеру, истинными будут высказывания: «Ни один павлин не относится к числу певчих птиц», «Ни один человек младше восемнадцати лет не является совершеннолетним в России». Пример ложного высказывания: «Ни один гуманитарий не разбирается в математике». Высказывание ложно, так как термины «гуманитарий» и «люди, разбирающиеся в математике» не находятся ни в отношении противоречия, ни в отношении соподчинения.
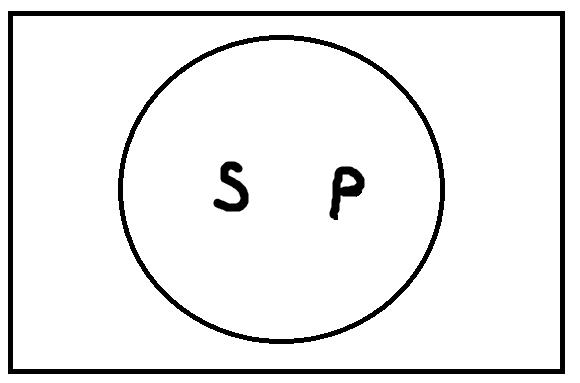
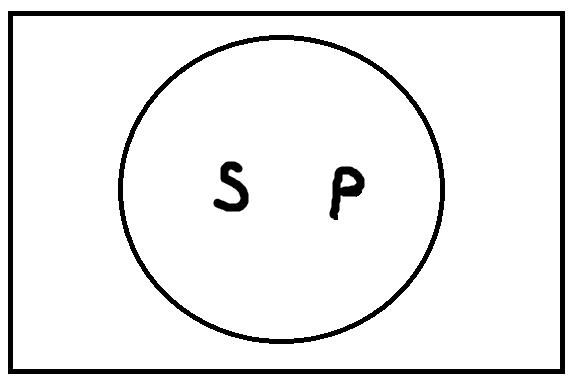
Частноутвердительные высказывания формы «Некоторые S есть P» истинны, если термины S и P находятся в следующих отношениях:
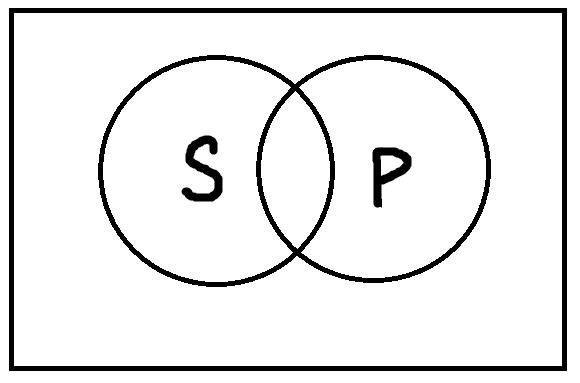
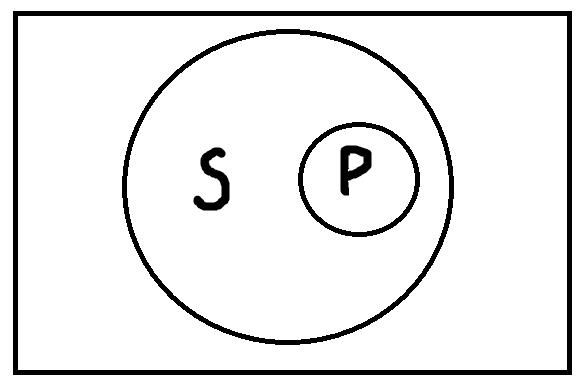
Частноутвердительные высказывания будут ложными, только если термины S и P находятся в отношении противоречия или соподчинения: «Некоторые тракторы – это самолёты», «Некоторые ложные высказывания истинны».
Частноотрицательные высказывания типа «Некоторые S не есть P» истинны, если термины S и P находятся в следующих отношениях:
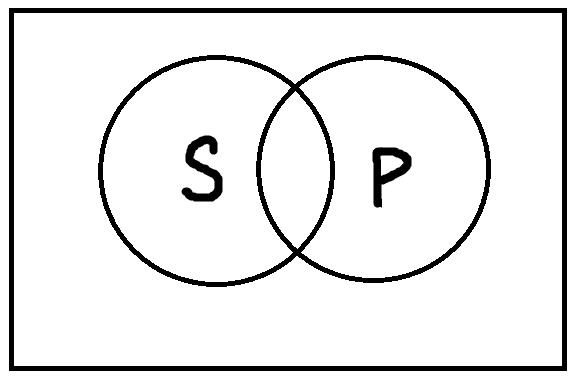
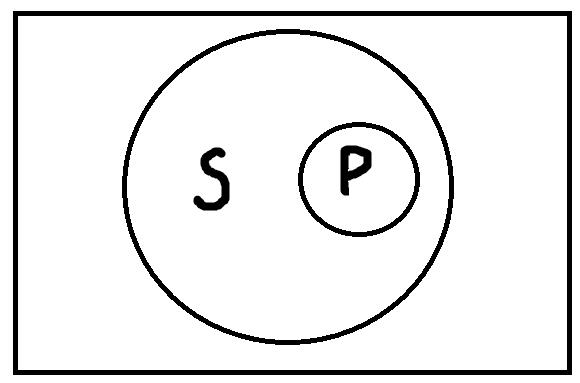
Это отношения: пересечения, дополнительности, включения, противоречия и соподчинения. Очевидно, что первые три отношения совпадают с тем, что было верно и для частноутвердительных высказываний. Все они как раз представляют случаи, когда некоторые S есть P, и в то же время некоторые S не есть P. Примеры подобных истинных высказываний: «Некоторые здоровые люди не употребляют алкоголь», «Некоторые наши работники из категории младше сорока ещё не достигли возраста и двадцати пяти», «Некоторые деревья не являются вечнозелёными».
По тем же причинам, по которым отношения равнообъёмности и обратного подчинения представляли собой условия истинности для частноутвердительных высказываний, отношения противоречия и соподчинения будут верны для частноотрицательных высказываний. Из высказывания, имеющего форму «Некоторые S не есть P» нельзя логично вывести высказывание «Некоторые S есть P». Однако из высказывания «Все S не есть P» можно перейти к высказыванию «Некоторые S не есть P», так как на основании информации, которой мы обладаем обо всех элементах объёмов терминов S и P, можно сделать вывод и об их отдельных представителях. Поэтому верными будут высказывания: «Некоторые журналы не являются книгами», «Некоторые глупцы не являются умными» и т.п.
Частноотрицательные высказывания будут ложными, только если термины S и P находятся в отношениях равнообъёмности и обратного подчинения. Примеры ложных высказываний: «Некоторые рыбы не умеют дышать под водой», «Некоторые яблоки не являются фруктами».
Итак, мы выяснили, при каких условиях высказывания той или иной формы будут истинными и ложными. При этом стало понятно, что не всегда истинность и ложность высказываний с логической точки зрения совпадает с нашими интуитивными представлениями. Иногда одинаковые на первый взгляд высказывания оцениваются совершенно по-разному, так как за ними скрываются разные логические формы и, следовательно, разные отношения между входящими в них терминами. Эти условия истинности важно запомнить. Они пригодятся, когда в следующем уроке мы научимся складывать высказывания в цепочки рассуждений и будем пытаться найти такие формы умозаключений, которые будут всегда правильными.
Игра «Пересечение множеств»
В этом упражнении вам нужно внимательно прочитать текст задания и правильно расположить множества, соответствующие понятиям.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Упражнения
Прочитайте следующие категориальные атрибутивные высказывания. Определите, к какому типу они относятся. С помощью диаграмм покажите, истинны они или ложны.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.