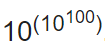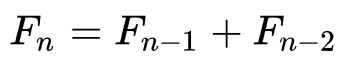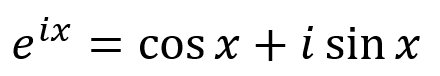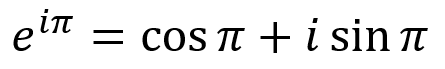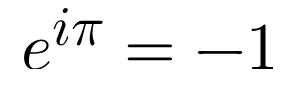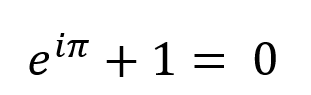Что такое интересное число
Удивительное в математике
Математика – сложная, но очень занимательная наука, с которой мы знакомимся еще в школе, а затем пользуемся и в повседневной жизни. Если присмотреться, то она окружает нас повсюду: мы подсчитываем сумму покупок, режем торт на определенное количество кусочков, определяем время. На самом деле, математика – это не только непонятные теории и заумные гипотезы ученых. Несмотря на всю серьезность этой науки, удивительные факты из мира математики встречаются сплошь и рядом. Они будут интересны не только ученым, но и всем людям, которым интересно узнавать интересную информацию.
Из истории математики
Десятеричная система исчисления прижилась у людей потому, что именно пальцы рук, которых, как известно 10, использовались первоначально для подсчетов. Но у цивилизаций майя и чукчей раньше была в ходу двадцатеричная система исчисления, поскольку они использовали в счете пальцы не только рук, но и ног.
Автором знака «=» является математик XVI в. Роберт Рекорд, которому просто надоело писать в каждом уравнении слово «равно».
Некоторые считают, Альфред Нобель застал свою жену за изменой с математиком, поэтому в перечне дисциплин одноименной премии математика отсутствует. Удивительный факт, но в действительности Нобель даже не был ни разу женат. Что касается причин, то доподлинные так и остались неизвестными, а среди возможных предположений выдвигаются следующие:
Все современные математические знания с трудом можно уместить в 100 000 учебников, тогда как в 1900 г. для этого понадобилось бы не более 80 книг.
О цифрах и числах
Если сложить все числа от 1 до 100, их сумма будет равна 5050.
2 и 5 – единственные простые числа (то есть те, которые делятся только на сами себя и на 1) которые заканчиваются на 2 и 5.
Зеркальные числа, то есть те, что читаются в обеих направлениях одинаково, имеют название палиндромы (к примеру, 12321 или 4567654).
Самое большое число в мире, которое имеет название и встречается в словарях, пишется как 1 и 600 нулей (или 10 600 ) и называется центиллион.
Самое маленькое число пока существует без названия и является десятичной дробью, у которой сразу после запятой и перед 1 следует 100 миллионов триллионов триллионов триллионов нулей. Ученые используют его только для вычисления вероятности развития новой Вселенной из любого атома.
Самым мистическим считается 666 – как говорится в одном из стихов книги Откровения, знак антихриста. С ним связаны различные удивительные факты не только в математике, но и в повседневной жизни:
Магия цифр
0 – удивительная цифра в математике, поскольку только ее невозможно записать с помощью римских цифр.
18 – единственное число, в котором в результате сложения составляющих его цифр получается сумма в 2 раза меньшая него самого.
Чтобы проверить, делится ли на 3 число, нужно сложить все его цифры и проверить, делится ли полученная сумма делится на 3.
Миг или момент – вполне реальная единица времени, продолжительность которой составляет 1/100 секунды.
Удивительная цифра 9 имеет особое свойство: если сначала умножить на 9 любое число, а затем складывать составляющие его цифры до тех пор, пока не получится однозначная цифра, то получаемая сумма всегда равна 9.
2520 – минимальное число, которое делится на любое число от 1 до 10 без остатка.
Если умножить собственный возраст сначала на 7, а затем на 1443, то в результате получится число, которое будет означать возраст, написанный трижды подряд.
Отношение к цифрам в разных странах
С 1995 г. в Тайване на законодательном уровне закреплено разрешение жителям не использовать цифру 4 (например, при нумерации этажей зданий). Это объясняется тем, что китайское название этой цифры звучит одинаково со словом «смерть», поэтому большинство зданий не имеет 4-го этажа, и, соответственно, в лифтах нет такой отметки.
Тайское произношение цифры 5 звучит как «ха», поэтому во время общения по интернету некоторые тайцы используют сленг «555», что равнозначно нашему «ха-ха-ха».
Особенно религиозные евреи отвергают все, что так или иначе может напоминать о христианстве. Удивительный факт, но на математике ученики некоторых школ даже не используют в вычислениях знак «+», а заменяют его символом, похожим на перевернутую вверх букву «т».
17 вызывает у большинства итальянцев неприязнь, которая идет еще с периода древней римской Империи. На надгробиях тех времен обычно писали фразу «меня больше нет», которая изображалась в виде «VIXI» — именно так выглядят цифры 6 и 11 по римскому обозначению, а в сумме они дают 17.
По данным социологических опросов с счастливой цифрой у большинства людей из разных стран мира ассоциируется 7, а на втором месте – 3. Практически во всех религиях и культурах цифра 7 несет в себе положительную энергетику.
Несчастливая репутация у числа 13 часто связывается с Тайной Вечерей, на которую было приглашено 13 гостей во главе с Иисусом, а 13-м гостем был Иуда Искариот.
Бытовые факты
По подсчетам математиков существует 177 147 возможных способов для завязывания галстука, правда история умалчивает о том, как образом они пришли к такому результату: опытным путем или с помощью вычислений.
Компьютерный пасьянс «Солитер» («Свободная ячейка») считается одним из самых легких с математической точки зрения, поскольку вероятность того, что выпадет решаемый расклад – 99,99%.
Американские исследователи обнаружили удивительный факт: по тестам по математике лучшие результаты показывают студенты, которые во время их написания жуют жвачку.
Сумма точек, располагающихся на противоположных сторонах на игральной кости, всегда равна 7.
Если в группе находится 23 или более человек, то вероятность, что у двоих из них день рождения приходится на один день превышает 50%, тогда как для группы от 60 человек этот показатель приближается к 99%.
Существует 2 способа разрезать торт 8 равных частей, сделав только 3 касания ножа.
Каждый раз во время перемешивания стандартной карточной колоды образуется последовательность, которая, вероятнее всего, ранее ни разу не выпадала. Количество возможных комбинаций расположения карт составляет 8х10 67 или 52!. Чтобы получить минимум 50% вероятность повторного выпадения комбинации, понадобится перемешать карты 9х10 33 раз.
Число «пи» имеет два собственных праздничных дня: 14 марта (у американцев эта дата записывается кратко как 3.14) и 22 июля (поскольку 3.14 – это результат деления 22 на 7).
Рекламная кампания американской сети фаст-фудов A&W закончилась провалом по банальной причине. Они рекламировали гамбургер весом 1/3 фунта, который стоил дешевле аналогичного продукта из Макдональдса весом 1/4 фунта. К тому же по мнению покупателей новый сэндвич был более вкусным. Позднее выяснился удивительный факт: именно незнание математики (а именно дробей) потенциальными клиентами привело к неудаче. Большинство покупателей посчитало предложение невыгодным, основываясь на том, что 3 меньше, чем 4.
Красота и математика: 13 фантастических чисел, которые нас окружают
О числах и математических терминах, которые будут интересны не только математикам.
Нередко числа находятся с помощью красивых уравнений и формул. А еще они могут обладать математической красотой. Это значит, что их свойства ведут к непредсказуемому результату — привлекательному как визуально, так и интеллектуально.
Ниже мы обсудим 13 удивительных чисел и понятий, от бесконечности до золотого сечения, которые доказывают, что математика — тоже своего рода искусство.
13. Алеф-ноль ℵ0
Алеф-ноль — это наименьшее бесконечное кардинальное число. Возможно, вы подумаете: как же так? Ведь бесконечность — это всего лишь понятие, а не множество бесконечных чисел. В конце концов, если и существует бесконечность, которая больше другой бесконечности, то первая — уже определенно не бесконечность.
Сейчас разберемся. Предположим, у нас есть базовое представление о том, что такое бесконечность (см. пункт 12). Алеф-ноль — это множество натуральных чисел (0, 1, 2, 3 и т. д.). Это понятие (или число) велико по размеру и, в общем-то, бесконечно.
Что, если мы пересчитаем все натуральные числа два или три раза? После завершения первого множества мы получим числа, выходящие за рамки натуральных чисел по порядку. Итак, нам понадобится порядок чисел или порядковый номер. Следующее число после Алеф-ноль — это омега (ω). Затем идет ω + 1. Эти два последних числа — не кардинальные числа, а порядковые (ординалы): то есть они показывают положение элементов относительно горизонтальной оси. График ниже — их упрощенное представление.
Каждое множество чисел может представлять набор множеств натуральных чисел с мощностью ℵ0. Если добавить к первому множеству единицу — это не изменит количество элементов (вы даже можете просто изменить порядок, и у вас все равно останется мощность Алеф-ноль).
Это позволяет рассматривать их как порядковые величины (ординалы). Следовательно, первое порядковое трансфинитное число после набора — это то, что мы обсуждали выше — омега «ω». Интересно и то, что число ω + 1 необязательно больше ω — оно просто идет после него.
Да, возможно, это слишком для мгновенного понимания. Это то, о чем следует размышлять и к чему следует возвращаться. Поэтому ниже мы расписали все, что вам нужно знать:
А Алеф-ноль — всего лишь первый кардинал из огромного множества других «Алефов».
12. Бесконечность ∞
Это скорее идея или концепция, чем число. Этот символ часто называют лемнискатой. Прежде чем обсуждать характеристики и интересные факты о бесконечности, важно отметить, что число π (см. пункт 4) считается одной из ее форм. Конечно, под этим мы подразумеваем диапазон чисел после запятой в 3,14159… Вот почему бесконечность — это понятие, а не то, что можно выразить количественно. Другой пример: прекрасное поле фракталов. Возьмем, к примеру, простую снежинку Коха, которую можно разделить на бесконечно малые «хлопья» одинаковой формы.
Интересно и то, что, когда мы думаем о бесконечности, мы представляем постоянно растущую меру, но она не расширяется и не становится больше. Она такая, какая есть.
Обсудим две простые темы, связанные с бесконечностью (те, которые не требуют мощной мозговой активности):
Верно ли, что 0,99999 = 1?
Учитывая, что после запятой у нас есть девятки, которые стремятся к бесконечности, мы можем предположить, что 0,99999 приблизительно равно 1. Но существует и алгебраическое доказательство:
10x = 9,9999
Если вычесть x с каждой стороны, то получим:
9x = 9
Разделим обе стороны на 9 и получим, что:
x = 1
Немного странно, вы не находите?
Любое число, вычтенное из самого себя, даст ноль. Но ведь бесконечность — это не число. Значит, попробуем провести «тест»:
Добавим по 1 с каждой стороны:
Зная, что ∞ + 1 = ∞, упростим уравнение:
В школе нас также учат, что мы не можем делить на 0. Нам говорят, что 1 : 0 не имеет смысла. Что ж, это утверждение нельзя назвать неверным, но в то же время оно не отражает всей истины. Просто подумайте: если вы разделите 1 яблоко на 0 человек, сколько людей вам понадобится, чтобы съесть фрукт? Это форма бесконечности, которая никогда не разрушается.
Итак, получается 1 : 0 = ∞. Тогда почему нас учат, что результат не определен и не имеет смысла?
Итоговая таблица для вычислений с бесконечностью:
Буква i обозначает мнимое число. Это такое число, квадрат которого дает отрицательный результат. Это не то, о чем мы обычно думаем при возведении чисел в квадрат, потому что мы знаем, что умножение двух одинаковых чисел всегда дает положительный результат. Но это не мешает нам создать аксиому, которая бы изменила правила игры. Мы называем их воображаемыми, потому что их просто не должно быть.
Концепция мнимых чисел проста. Мы представляем, что они существуют. Чем они полезны? Мы можем решать уравнения, для которых нужен квадратный корень из отрицательного числа.
x 2 + 1 = 0
x = ± i
Есть и другое использование мнимых чисел: их объединяют с натуральными для получения комплексных чисел (например, 7i + 12), а также используют в электричестве.
10. Гугол
Гугол — это число в десятичной системе счисления, который изображается единицей со 100 нулями. И вот так оно выглядит: 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. Или:
А еще его можно представить в виде факториала 70! — то есть 70 x 69 x 68 x 67 x 66 x 65 x 64 x 63 x 62 x 61 x 60 x 59… х 1
Чтобы еще больше вас запутать, существует число под названием «гуголплекс». Это 10 в степени гугол:
Интересный факт: название компании Google представляет собой неправильное написание числа. Хитроумный способ назвать поисковую систему. Число в основном используется в астрономических исследованиях, в частности, в альтернативе теории Большого Взрыва — в Большом замораживании.
9. Цифра 9
Любимое число всех маркетологов (вспомните ценники) и красивое визуально и математически. В геометрии оно часто прячется во многих местах. Например, возьмем круг:
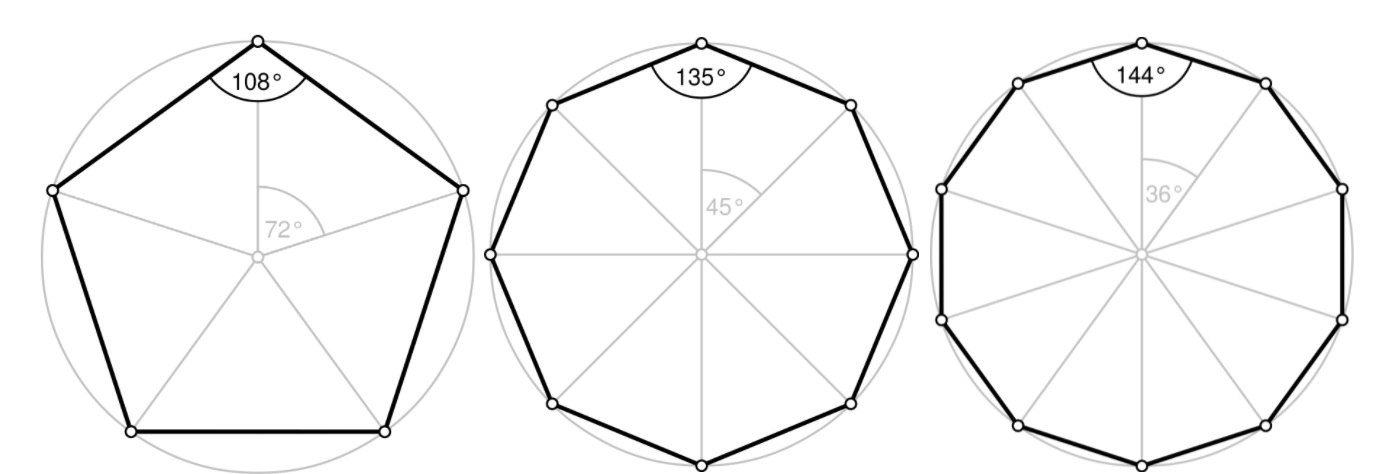
Еще несколько фигур с обозначением углов:
Слева направо: Пентагон, Октагон, Декагон.
Отвлечемся от геометрии. Если сложить цифры, которые предшествуют девяти, то получим 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. И вновь: 3 + 6 = 9
Если умножить цифры, предшествующие 9, на девять и сложить их элементы, сумма будет всегда равна 9. А вот и примеры:
Разделив цифры на 9, мы всегда получим одну и ту же цифру, повторяющуюся до бесконечности:
8. Число 73
Если вы фанат «Теории Большого взрыва», то, должно быть, вы помните, как Шелдон Купер объяснял, почему 73 — идеальное число:
«Самое замечательное число — 73. Вы, скорее всего, теряетесь в догадках почему. 73 — это 21-ое простое число. Его зеркальное отражение 37 является 12-ым, чье отражение 21 является результатом умножения, не упадите, 7 и 3».
«В двоичной системе 73 — еще палиндром. 1001001, что справа налево читается, как 100100».
Все эти цитаты — из 10 серии 4-го сезона сериала, которая, по определенному стечению обстоятельств, ялвяется 73-м эпизодом сериала (а еще годом рождения Джима Парсонса, актера, сыгравшего Шелдона).
7. Число Эйлера
Названное в честь Леонарда Эйлера, e — иррациональное число и основание натуральных логарифмов. Интересно, что число Эйлера известно с точностью до 1 триллиона цифр. А найти его можно с помощью этой формулы:
Когда n приближается к бесконечности, мы получаем более ясное представление о значении e. Когда n = 100000, e = 2,71827.
Еще одно удивительное свойство e — его наклон является его же значением. Оно также используется в финансах для расчета сложных процентов.
6. Последовательность Фибоначчи
Леонардо Боначчи, также известный как Фибоначчи (это прозвище, означающее «сын Боначчи»), создал одну из самых увлекательных последовательностей в нашей вселенной. И для этого он использовал простые методы сложения, наблюдая за популяциями кроликов.
Несмотря на то, что есть несколько свидетельств, которые говорят о том, что индийские математики вывели последовательность намного раньше, предлагаем придерживаться широко признанного факта, что ее автор — Фибоначчи.
Получить числа Фибоначчи можно с помощью простой формулы для n > 2:
Так, мы получаем последовательность, которая уходит в бесконечность:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,….
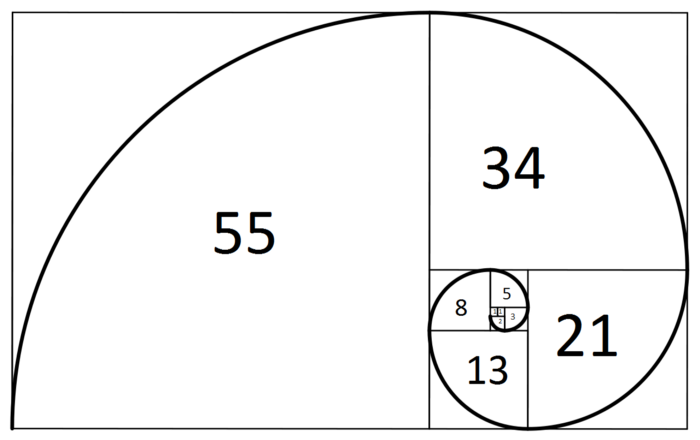
Ее прелесть в том, что она связана с природой. Например, ее можно обнаружить в цветении артишока и некоторых цветов вроде ромашек.
А что насчет Галактики? Гэри Б. Мэйснер выдвинул интересное и фактически обоснованное предположение, согласно которому размеры Земли и Луны находятся в соотношении Фи, образуя Треугольник, основанный на 1,618.
Но что такое Фи, и что за 1,618?
Если взять два любых последовательных числа в последовательности, их отношение (Xn / Xn-1) приблизится к 1,618. Это число называется Фи — в честь древнегреческого скульптора и архитектора Фидия — или «золотым числом»:
317 811 : 196 418 = 1,61803
Стремясь к бесконечности, значения отношений приближаются к 1,618.
5. Число 23
Наверное, многие видели фильм «Роковое число 23», в котором Джим Керри играет Уолтера Спэрроу — человека, который становится одержимым числом 23, после того как читает о нем в книге. Считается, что это число таинственным образом совпадает со многими событиями по всему миру, и, хотя это можно назвать наглядным примером Апофении, все-таки интересно перечислить некоторые «случайности»:
4. Пи (π) и Тау (τ)
Знаменитое иррациональное число, представляющее отношение длины окружности к ее радиусу. Сложно найти человека, который никогда его не видел.
Если мы нарисуем круг диаметром 1, тогда длина окружности будет равна 3,14159… что просто обозначается буквой π. Это длина окружности по диаметру.
А теперь к интересным свойствам:
А причем здесь Тау? Некоторые математики спорят над «полезностью» π и предлагают использовать вместо него тау (τ), которое равно 2π. По их словам, оно лучше подходит для вычисления кругов. Если вникнуть в детали, интуиция их не подводит. Но разве можно не любить π?
Кстати, ежегодно 14 марта отмечается день числа Пи (дата в США пишется в виде MM / DD — получается, 3/14).
3. Тождество Эйлера
А вот и главная причина, по которой в заголовке статьи фигурирует слово «красота». Сочетание красивейших математических концепций обычно дает простые результаты. Но для начала вспомним, о каких концепциях идет речь и как мы собираемся их объединить:
Но как это вышло?
Если переместить приведенную выше формулу Эйлера на комплексную плоскость (с настоящими и мнимыми числами), мы получим окружность. Включив в уравнение радиус r, мы сможем преобразовать точки в другую форму, например, возведя re в степень ix.
Если мы предположим, что x = π, то получим следующее:
Мы можем вновь изменить это уравнение, чтобы сделать его более красивым, и добавить еще одно простое число:
Это число, также известное как Постоянная Капрекара, имеет отличительную особенность. Вы поймете, какую, когда выполните следующие шаги:
Если вы будете повторять эти шаги, вы всегда будете получать 6174 — и это настоящая загадка.
Почему всегда выходит 6174, независимо от того, с каких чисел вы начнете? Давайте разберемся.
Возьмем, к примеру, 2714:
Теперь, когда мы получили 6174, мы больше не сдвинемся с этой точки. Потому что 7641-1467 = 6174.
А еще 6174 — число Харшада. Это значит, что оно делится на сумму его составляющих: 6174 / (6 + 1 + 7 + 4) = 6174/18 = 343.
1. Золотое сечение
Пожалуй, это самое важное соотношение в мире. Напоминаем: его вывели греки. А вот список его основных характеристик:
Бонус
На самом деле самое большое число из существующих — 40. А вот и доказательство:
13 самых знаменитых чисел
Арифметика на грани астрологии.
Дизайнеры всего мира знают: чёрный — цвет скорби, зелёный — цвет спокойствия, а голубой — цвет динамичного развития компании, молодой коллектив которой бесстрашно смотрит в будущее и не боится задержек зарплаты. И дизайнерам всего мира приходится с этими догмами работать.
Такая же история и с числами: в Китае не бывает 4-х этажей (звучит как «смерть»), 18-й — самый долгожданный день рождения, а длина и радиус одной окружности никогда не будут целыми числами одновременно. Список из самых интересных и загадочных чисел прилагается:
Пи: 3,14
Известная всем со школы константа, определяющая коифициент отношения длинные окружности к радиусу. Единственное число в списке, имеющее собственный праздник: 14 марта (то есть 3 месяц, 14 число).
Число действительно очень интересное, математики продолжают изучать его свойства до сих пор. Например, Пи — удивительно нормальное число. То есть в его десятичной записи на 200 млн знаков после запятой примерно равномерно встречаются все десять цифр.
Число Эйлера (e): 2,71
Ещё одна школьная константа, более известная, как основание логарифма. Так же как и Пи, вызывает неугасающий интерес учёных, и примерно те же самые вопрос. Кроме того, математикам так и не удалось обосновать какую-то связь Пи и e.
666
В Библии фигурирует как «число, под которым скрыто имя зверя Апокалипсиса». «Здесь мудрость. Кто имеет ум, тот сочти число зверя, ибо число это человеческое; число его шестьсот шестьдесят шесть». (Отк. 13:18). Какого именно зверя — не очень ясно, потому что в «Откровении Иоанна Богослова» их четыре: орел, лев, ангел и бык. Число стало символизировать что-угодно антихристианское, и его немедленно забронировали себе в качестве официального атрибута сатанисты.
Как считают некоторые теологи, в числе зашифровано имя, но какое именно — не ясно.
К слову, в Библии три шестерки встречаются три раза и в «Ветхом завете».
13
Историки не могут точно сказать, откуда взялась боязнь числа 13, но, чтобы не выглядеть глупо, придумали явлению название — «трискайдекафобия». Самая известная версия — это отсылка к Библии, на Тайной вечере Иуда был 13-м.
Уровень боязни числа прямо пропорциональна религиозности страны: больше всего попыток заменить число 13 разными способами (12+1, 12B и т.п.) в Италии и США.
18
Возраст совершеннолетия в самом большом количестве стран. Чаще всего после этого возраста молодым людям разрешают голосовать, заключать браки, начинать собственное дело и платить налоги.
Очевидно, что 18 оборотов вокруг Солнца, которые сделал гражданин никак не гарантируют его дееспособность, поэтому до сих пор остаётся предметом спора.
Гугол
Это единица с сотней нулей после неё. Название в шутку придумал математик Эдвард Казнер в 1938 году, когда гулял с племянниками, а те донимали его вопросом «какое самое большое число?» 60 лет спустя два молодых человека назвали так собственный поисковый движок.
Ноль
Самое важное, что нужно знать про ноль — это то, что него нельзя делить. На компьютерах и калькуляторах эта функция заблокирована, потому что может сломать Вселенную.
8
7 — счастливое число в Западной культуре (тоже по библейским мотивам), но надежды, возлагаемые на него, не могут сравниться с тем, как боготворят восьмёрку Китайцы. На мандарине цифра 8 (八) читается как «ба», что созвучно с иероглифом 发, который читается как «фа». У него невероятное количество значений, но китайца больше всего интересует комбинация 发财 — богатеть. Почти все цены в Китае заканчиваются на восьмерку, а половина работодателей выплачивает зарплату суммами, заканчивающимися на 88. Потому восьмерок в Китае много не бывает.
Золотое сечение: 1,618
Самое творческое число, популяризированное Леонардо да Винчи. Встречается практически везде: и в химических структурах, в биологии, физиологии и т.д.
В реальной жизни начали применять ещё до изобретения самого термина «математика». Самый известный пример — пропорции египетских пирамид.
Числа Фибоначчи: 1, 1, 2, 3, 8, 13, 21, …
Ряд Фибоначчи — это по сути выраженное числами золотое сечение. Записывается очень легко: первые два числа — это единицы, а каждое последующее — это сумма предыдущих.
Последовательность придумали в Древней Индии, но в Европе её популяризовал Леонардо Пизанский в XI веке н.э. Эта последовательность чисел очень часто встречается в природе: согласно этой формуле располагаются семена подсолнуха, семена в шишках, ячейки ананаса и т.д. Даже длины фаланг пальцев у человека подчинены этой последовательности.
43252003274489856000
Количество комбинаций трёхсекционного Кубика Рубика. Нынешний рекорд сборки составляет 3,47 секунд, то есть нынешний чемпион сможет перебрать их все всего за 4,8 млрд лет.
12
Дюжина долгое время претендовала на то, чтобы стать основой для универсальной системы исчисления. Отсюда и такое количество рядов с двенадцатью пунктами: часы, месяцы, апостолы (Иуда не считается), боги в греческом пантеоне, ступень колеса в буддизме, имамов в буддизме, дюймов в футе, пунктов в кегле, пенсов в шиллинге, и т.д.
Есть мнение, что десятеричная система закрепилась только из-за того, что у нас на руках 10 пальцев, но для двенадцатеричной системы существовал свой способ демонстрации чисел: по количеству фаланг на четырех (кроме большого) пальцах руки.
42
42 — это ответ на главный вопрос жизни, вселенной и всего такого по версии писателя-фантаста Дугласа Адамса. Получен в результате вычисления семи с половиной миллионов лет непрерывных вычислений на специальном компьютере «Думатель». Ответ должен был решить практически все проблемы Вселенной.
Развитые расы, получившие ответ 42 были несколько разочарованы, тогда «Думатель» предложил создать ещё более совершенный компьютер, который найдёт Окончательный Вопрос. Компьютер назвали Земля. Что было дальше — читай в романах серии «Автостопом по галактике».