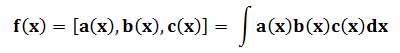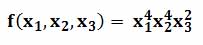Что такое группа в математике

Группа (математика)

Один из примеров группы — множество целых чисел, снабжённое операцией сложения: сумма любых двух целых чисел также даёт целое число, роль нейтрального элемента играет ноль, а число с противоположным знаком является обратным элементом. Другие примеры — множество вещественных чисел с операцией сложения, множество вращений плоскости вокруг начала координат. Благодаря абстрактному определению группы через систему аксиом, не привязанной к специфике образующих множеств, в теории групп создан универсальный аппарат для изучения широкого класса математических объектов самого разнообразного происхождения с точки зрения общих свойств их структуры. Вездесущность групп в математике и за её пределами делает их важнейшей конструкцией в современной математике и её приложениях.

Группа фундаментально родственна понятию симметрии и является важным инструментом в изучении всех её проявлений. Например, группа симметрии отражает свойства геометрического объекта: она состоит из множества преобразований, оставляющих объект неизменным, и операции комбинирования двух таких преобразований, следующих друг за другом. Такие группы симметрии, как точечные группы симметрии, помогают понять явление молекулярной симметрии в химии; группа Пуанкаре характеризует симметрию физического пространства-времени, а специальные унитарные группы применяются в стандартной модели физики элементарных частиц.

Понятие группы ввёл Эварист Галуа, изучая многочлены в 1830-е годы.

Современная теория групп является активным разделом математики. Один из наиболее впечатляющих результатов достигнут в классификации простых конечных групп, которая была завершена в 1981 году: доказательство теоремы составляет десятки тысяч страниц сотен научных статей более ста авторов, опубликованных с 1955 года, но статьи продолжают появляться из-за обнаруживаемых пробелов в доказательстве. С середины 1980-х годов значительное развитие получила геометрическая теория групп, изучающая конечно-порождённые группы как геометрические объекты.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Метри́ческим простра́нством называется непустое множество, в котором между любой парой элементов, обладающих определенными свойствами, определено расстояние, называемое ме́трикой.

Источник

Группы, кольца, поля в математике

Группа: определение и примеры групп

Множество с алгебраической операцией называется группой, если выполняются следующие условия:

1) операция в ассоциативна: ;

2) в существует нейтральный элемент ;

Решение. Действительно, операция умножения определена на указанном множестве, так как

Кольцо

1) относительно операции сложения множество — коммутативная группа, т.е.

а) операция сложения коммутативна: ;

б) операция сложения ассоциативна: ;

в) существует нулевой элемент ;

г) для каждого элемента существует противоположный ему элемент ;

2) операция умножения в множестве ассоциативна:

3) операции сложения и умножения связаны законами дистрибутивности:

Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.

Если операция коммутативна, то дистрибутивность слева операции относительно операции влечет дистрибутивность справа, так как

Решение. В самом деле, для любых положительных действительных чисел справедливы равенства

Следовательно, операция дистрибутивна справа относительно операции умножения чисел. Дистрибутивность слева относительно умножения опровергается примером

Пример В.7. Доказать, что множество чисел вида, где и — целые числа, является кольцом:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.2) имеют тоже самое представление:

Таким образом, рассматриваемое множество удовлетворяет всем условиям определения кольца.

Поле: определение и примеры полей

1) — коммутативное кольцо с единицей ;

Как видим, поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.

Пример В.8. На множестве трех целых чисел определим две операции:

1) «сложение по модулю 3» — остаток от деления суммы на 3 (обозначим через );

2) «умножение по модулю 3» — остаток от деления произведения на 3 (обозначим через ).

Доказать, что множество является полем относительно введенных операций.

– остаток от деления на 3 суммы не изменится, если слагаемое (или не сколько слагаемых) заменить его остатком при делении на 3:

– остаток от деления на 3 произведения не изменится, если множитель (или несколько множителей) заменить его остатком при делении на 3:

Рассматриваемые в примере операции «сложения по модулю 3» и «умножения по модулю 3» можно представить в виде

Покажем, что множество является коммутативным кольцом с единицей. В самом деле, операция «сложения по модулю 3» коммутативна и ассоциативна. Это следует из коммутативности и ассоциативности сложения чисел. Действительно, из равенства следует, что

Коммутативность доказана. Заметим, впрочем, что коммутативность «сложения по модулю 3» видна непосредственно по таблице (см. рис.В.2): слагаемые и в таблице можно поменять местами, при этом таблица не изменится.

Из равенства следует, что

Ассоциативность «сложения по модулю 3» доказана.

Итак, множество относительно операции «сложения по модулю 3» является коммутативной группой.

Операция «умножение по модулю 3» ассоциативна и коммутативна, что следует из ассоциативности и коммутативности умножения целых чисел, а также свойств остатков:

Следовательно, операция «умножения по модулю 3» дистрибутивна слева относительно операции «сложения по модулю 3». Дистрибутивность справа можно не проверять, так как обе операции коммутативны.

Единичным элементом служит число 1 (что видно по таблице «умножения по модулю 3»). Следовательно, — коммутативное кольцо с единицей.

Пример В.9. Доказать, что множество чисел вида, где и — рациональные числа, является полем:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.З) имеют тоже самое представление:

Так как рассматриваемое множество является коммутативным кольцом с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно является полем.

Источник

Группа (алгебра)

Гру́ппа — в абстрактной алгебре непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Ветвь математики, занимающаяся группами, называется теорией групп.

Всем знакомые вещественные числа наделены сложением — операцией, обладающей некоторым набором свойств. Похожими свойствами обладают и многие другие из объектов, которые изучает математика, — например, множество вращений плоскости вокруг начала координат. Теория групп занимается изучением взаимосвязей между этими свойствами в общем виде. Структура группы включается в различные другие алгебраические структуры, такие как поля, векторные пространства или группы Ли. Кроме того, группы являются важными инструментами в изучении симметрии во всех её проявлениях.

Содержание

Определения

Комментарии

Связанные определения

Примеры

Стандартные обозначения

Мультипликативная запись

Обычно групповую операцию называют (абстрактным) умножением; тогда применяется мультипликативная запись:

Аддитивная запись

В коммутативной группе определяющяя операция часто рассматривается как (абстрактное) сложение и записывается аддитивно:

Простейшие свойства

Получение новых групп из уже известных

Обобщения

См. также

Популярная литература

Научная литература

Ссылки

Полезное

Смотреть что такое «Группа (алгебра)» в других словарях:

Алгебра Хопфа — Алгебра Хопфа алгебра, являющаяся унитарной ассоциативной коалгеброй и, таким образом, биалгеброй c антигомоморфизмом специального вида. Названа в честь Х. Хопфа. Алгебры Хопфа встречаются в алгебраической топологии, где они возникли в… … Википедия

ГРУППА — множество, на к ром определена операция, наз. умножением и удовлетворяющая спец. условиям (групповым аксиомам): в Г. существует единичный элемент; для каждого элемента Г. существует обратный; операция умножения ассоциативна. Понятие Г. возникло… … Физическая энциклопедия

Группа Ли — Группа (математика) Теория групп … Википедия

Группа Шрёдингера — Группа Шрёдингера это группа симметрии свободного уравнения Шрёдингера. Содержание 1 Алгебра Шрёдингера 2 Роль группы Шрёдингера в математической физике … Википедия

Группа Гейзенберга — группа, состоящая из квадратных матриц вида где элементы a, b, c принадлежат какому либо коммутативному кольцу с единицей. В качестве такого кольца R чаще всего берется: кольцо вещественных чисел так называемая непрерывная группа Гейзенберга,… … Википедия

Алгебра Темперли — Алгебра Темперли Либа, в статистической механике алгебра, при помощи которой строятся некоторые трансфер матрицы. Открыты Невиллом Темперли и Эллиотом Либом. Также алгебра применяется в теории интегрируемых моделей, имеет отношение… … Википедия

АЛГЕБРА МЕР — алгебра М(G).комплексных регулярных борелевских мер на локально компактной абелевой группе G, имеющих ограниченную вариацию, с обычными линейными операциями и сверткой в качестве умножения (см. Гармонический анализ абстрактный). Свертка полностью … Математическая энциклопедия

АЛГЕБРА С ДЕЛЕНИЕМ — алгебра Анад полем F, для любых элементов и bк рой уравнения разрешимы в А. Ассоциативная А. с д., рассматриваемая как кольцо, является телом, а ее центр С полем и Если то А. с д. Аназ. центральной А. с д. Конечномерные центральные ассоциативные… … Математическая энциклопедия

ГРУППА СУСЛОВИЕМ КОНЕЧНОСТИ — группа, элементы или подгруппы к рой удовлетворяют тому или иному условию конечности. Под условием конечности в теории групп понимается любое такое свойство, присущее всем конечным группам, что существуют бесконечные группы, к рые им не обладают … Математическая энциклопедия

Источник

Группа (математика)

Существуют математические объекты не являющиеся числами, но над ними мы имеем возможность совершать алгебраические действия. Свойства этих действий напоминают свойства действий над числами. Это делает необходимой сформулировать более общие понятия.

Определение 1. Полугруппой называется множество, в котором определено действие, сопоставляющее каждой упорядоченной паре элементов этого множества третий элемент − результат действия. Предполагается, что действие ассоциативно, т.е.

где ○− знак действия.

Если операция коммутативна, т.е.

Рассмотрим примеры групп:

1. Множество всех целых чисел относительно сложения.

Действительно, операция сложения ассоциативна (a+b)+c=a+(b+c). Нейтральным элементом является 0 (a+0=0+a=a). Наконец, обратным для элемента а является −a ( a+(−a)=(−a)+a=0).

2. Множество положительных рациональных чисел относительно умножения.

Покажем, что это множество удовлетворяет всем трем пунктам определения 2. Ассоциативность очевидна ( (ab)c=a(bc) ). Нейтральным элементом является 1 ( a·1=1·a=a ).И, наконец, обратным элементом для a является ().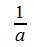

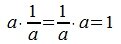
3. Множество квадратных матриц относительно сложения.

Ассоциативность сложения очевидно следует из правил сложения матриц (a+b)+c=a+(b+c). Нейтральным элементом является нулевая матрица, а обратным (противоположным) элементом является нулевая матрица.

Все вышеизложенные примеры групп являются также коммутативными. Приведем пример некоммутативной группы.

4. Множество квадратных невырожденных матриц относительно умножения.

Действительно. Ассоциативность умножения матриц сохраняется. Нейтральным элементом является единичная матрица. Единичная матрица является невырожденной, умножение невырожденных матриц будет невырожденным, следовательно всегда существует обратная матрица. При множестве матриц порядка n≥2 мы имеем дело с некоммутативной группой т.к. умножение матриц в общем случае некоммутативна ab≠ba.

Источник

Теория групп

Математическая теория групп, это одна из центральных концепций математики. Теория групп связывает разные разделы математики в такой же степени, как и понятия числа и функции.

Здесь я попробую рассказать о теории групп как можно проще с большим количеством примеров. Сначала дам определение того, что такое математическая группа. А потом расскажу про каждый термин из этого определения.

Определение группы

Сочетание множества и операции

Таким образом, для группы нам необходимо и множество и какая-то операция между элементами этого множества. По отдельности множество без операции не может быть группой. И операция без множества тоже не может быть группой.

Например, множество всех рациональных чисел, это множество, но не группа, так как не сказано, какая операция задана на этом множестве. Точно также множествами, но не группами являются множество всех треугольников или множество всех поворотов вокруг точки в трехмерном пространстве, так как мы еще не задали операцию между элементами этого множества.

Если мы говорим просто об операциях без конкретизации множества, то это тоже не группа. Например, такие операции, как сложение или параллельный перенос не являются группой, так как не задано, с элементами каких множеств они работают.

Еще одна особенность группы заключается в том, что в качестве группы рассматривается только одно сочетание множества и операции. Например, на множестве вещественных чисел можно определить много разных операций (сложение, вычитание, умножение и т.д.). Но в группе рассматривается только одна из этих операций. Другая операция на этом же множестве может представлять собой совсем другую группу.

То же самое можно сказать и относительно операции. Например, операция сложение может быть определена и на множестве целых чисел и на множестве рациональных чисел и на множестве вещественных чисел и т.д. На каждом из этих множеств операция сложения даёт свои группы.

Множество

Множеством в математике называется любой набор любых математических объектов. Причем, совсем необязательно, чтобы эти математические объекты были однотипными.

Но, как вы понимаете, очень трудно между такими неоднородными объектами множества ввести какую-то осмысленную операцию, которая имеет хоть какое-то практическое значение и применение. Поэтому для математических групп характерны однородные множества.

Примеры однородных множеств

Это могут быть, например, множества каких-то чисел. Например, множество всех комплексных чисел, или множество всех вещественных чисел больших 6 и меньших 14, или множество всех рациональных чисел, которые делятся на 3, и т.д.

В группах могут быть множества каких-то точек пространства. Например, в качестве элементов множества можно рассматривать все возможные квадраты на плоскости, или множество всех возможных кривых в 4-мерном пространстве, или множество всех точек какого-то конкретного отрезка и т.д.

Группы бывают на множествах каких-то векторов, тензоров, матриц и т.п.

В качестве множеств могут рассматриваться какие-нибудь преобразования пространства. Например, повороты, отражения, сжатия, смещения, кручения, параллельные переносы и т.п. Причем в одном групповом множестве могут быть одновременно, например, и повороты и растяжения пространства.

В качестве множества можно рассматривать, например, множество операций перестановок. Допустим, у вас есть какие-то объекты, которые как-то различаются между собой, например, разноцветные шарики или пронумерованные шарики. И эти объекты располагаются в каком-то первоначальном порядке. Например, если это пронумерованные шарики, то они могут располагаться в ряд или в ячейках, которые образуют квадратную решетку на плоскости или кубическую в пространстве. Вы можете взять два шарика и переставить их местами. Множество таких операций по перестановки двух шариков называется множеством перестановок.

Можно придумать много разных экзотических множеств. Например, множество всех комбинаций взвешивания монет на весах или множество всех перекрашиваний граней кубика или множество всех поворотов кубика Рубика или множество всех комбинаций граней кубика Рубика и т.п.

Типы множеств

Множества бывают конечные и бесконечные. Например, множество всех натуральных чисел меньших 10 является конечным. В этом множестве только 9 элементов. (В таких странах, как Россия и Германия число 0 не считается натуральным, в отличие, например, от Франции, где 0 признается натуральным числом.) А множество всех натуральных чисел является бесконечным. Еще пример бесконечного множества, это множество всех точек круга радиуса 5 см.

Для теории групп не имеет значение, конечное множество или бесконечное. Бывают группы на конечных множествах и на бесконечных множествах.

Множества бывают дискретные и непрерывные. Например, множество всех натуральных чисел или множество всех поворотов на угол кратный 90 градусов, это примеры дискретных множеств. А примерами непрерывных множеств являются, например, множество всех точек какого-то отрезка или множество всех параллельных переносов на любое расстояние и под любым углом к какому-то направлению.

Для теории групп не имеет значение, дискретное множество или непрерывное. Бывают группы на дискретных множествах и на непрерывных множествах.

В математике в качестве множества рассматривается и пустое множество, которое ничего не содержит. Математическая группа никогда не включает в себя пустое множество, так как для пустого множества остается неопределенной групповая операция между элементами такого множества.

А вот множество из одного единственного элемента может лежать в основе группы. На таком множестве можно ввести групповую операцию.

Подмножество

Подмножество какого-то множества, это любая часть этого множества. Другими словами, каждый элемент такого подмножества в свою очередь является одновременно еще и элементом множества.

Например, целые числа, это подмножество множества рациональных чисел, так как все целые числа являются одновременно и рациональными числами. А вот множество вещественных чисел не является подмножеством множества рациональных чисел, так как к вещественным числам относятся еще и иррациональные числа, которые не являются рациональными.

Если подмножество, в свою очередь, тоже содержит какие-то свои подмножества, то эти подмножества будут тоже подмножествами множества. («Подмножество моего подмножества является моим подмножеством.») Например, целые числа в качестве подмножества содержат натуральные числа. Но целые числа, это подмножество рациональных чисел. Значит, натуральные числа тоже являются подмножеством рациональных чисел.

Выделять подмножества можно как угодно. Например, подмножеством вещественных чисел является множество всех чисел больших числа (-5) и меньших числа (+6.87). Подмножеством множества всех поворотов на плоскости вокруг точки с координатами (0,0) является множество всех поворотов на угол кратный 60 градусов.

Таким образом, если множество, например, непрерывно и бесконечно, то его подмножества могут быть тоже непрерывны и бесконечны. А могут быть и дискретными и конечными.

Каждый элемент множества является его подмножеством.

Всё множество всегда является своим подмножеством.

Пустое множество всегда является подмножеством для любого множества.

Операция

В определении группы говорится, что операция должна быть бинарной и замкнутой. Разберемся с этими терминами.

Бинарная операция

Бинарная операция, заданная на множестве, это такая операция, для проведения которой требуется два элемента множества. В группах присутствуют только бинарные операции.

Такие хорошо знакомые операции, как операции сложения, вычитания, умножения и деления на множестве вещественных чисел являются бинарными операциями, так как для их проведения нужны сразу два числа. К бинарным операциям относятся скалярное произведение векторов и векторное произведение векторов.

Если мы имеем дело с каким-то множеством преобразований пространства (повороты, отражения, сжатия, растяжения, параллельный перенос и т.п.), то бинарную операцию для такого множества преобразований можно ввести просто, как последовательное выполнение двух преобразований. Аналогично, для множества перестановок бинарную операцию можно ввести как последовательное применение двух перестановок.

Наконец, любую функцию от двух переменных можно рассматривать, как бинарную операцию.

Обращаю внимание на то, что бинарная операция подразумевает, что она может действовать не только между разными элементами множества, но и между одним и тем же элементом множества. Например, если это операция умножения на множестве чисел, то мы можем перемножать не только разные числа (типа, 3*5=15), но и одно и то же число можем умножить на само себя (типа, 4*4=16). Именно поэтому существуют группы на базе множества, состоящего только из одного элемента, хотя групповая операция бинарная.

Коммутативность бинарных операций

Обратите внимание, что в некоторых бинарных операциях мы можем переставлять местами элементы множества, и результат выполнения операции от этого никогда не меняется. А в других операциях результат от такой перестановки может измениться.

В 3-мерном пространстве, в общем случае, повороты вокруг выделенной точки не являются перестановочными. (Иначе не было бы проблемы собрать кубик Рубика.) Но если выделить какую-нибудь ось, которая проходит через эту выделенную точку, то повороты вокруг такой оси будут перестановочными. Мы сначала можем сделать, например, поворот на 30 градусов вокруг такой оси по часовой стрелке, а потом на 45 градусов против часовой стрелки. И получим точно такой же поворот, как если делать все в другом порядке: сначала сделать поворот на 45 градусов против часовой стрелки, а потом на 30 градусов по часовой стрелке.

Бинарная операция является коммутирующей (или коммутативной) или перестановочной, если её результат всегда не зависит от порядка следования в ней элементов множества, на котором эта операция определена.

Другими словами, бинарная операция коммутирующая (перестановочная) если всегда AB=BA для любых элементов A и B рассматриваемого множества. Если равенство AB=BA нарушается хотя бы в одном случае, то это некоммутирующая (неперестановочная) операция на данном множестве.

Таким образом, нельзя просто сказать, что та или иная операция коммутирующая или нет, пока не определено то множество, на котором рассматривается данная операция. Например, нельзя сказать, коммутирует или нет последовательное выполнение поворотов, пока неизвестно, где рассматриваются эти повороты, на плоскости или в 3-мерном пространстве. На плоскости повороты коммутируют друг с другом. А повороты в 3-мерном пространстве не коммутируют, так как можно привести хотя бы один пример отсутствия такой коммутации.

Коммутирует ли произведение двух матриц? Это опять зависит от того, на каком множестве матриц мы рассматриваем операцию произведения двух матриц. Если это квадратные матрицы диагонального вида, тогда произведение таких матриц всегда коммутирует. А если это любые квадратные матрицы, то произведение матриц, в общем случае, не коммутирует.

Еще примеры коммутирующих и некоммутирующих операций. Скалярное произведение векторов всегда коммутирует: (A·B) = (B·A). Векторное произведение 3-мерных векторов не коммутирует: [AxB] ≠ [BxA].

Если групповая операция перестановочная, то такие группы называются коммутирующими (или коммутативными) группами или абелевыми группами (в честь норвежского математика Нильса Хенрика Абеля, который внес большой вклад в развитие теории групп).

Унарная операция

Унарная операция, заданная на множестве, это такая операция, для проведения которой требуется только один элемент множества.

Примерами унарных операций являются такие операции, как изменение знака числа, комплексное сопряжение, транспонирование матрицы, вычисление следа матрицы, вычисление определителя матрицы, вычисление длины вектора и другие подобные операции.

На базе унарных операций группы не бывают. Единственное исключение, это когда унарную операцию можно формально рассматривать, в качестве бинарной. Такая возможность может появиться в группах на базе множества с одним элементом.

Например, рассмотрим множество, состоящее только из одной симметричной квадратной матрицы A размера nxn. В этом случае транспонирование не меняет матрицы: A T =A. Поэтому формально введем бинарную операцию, которая работает так: AA = A T = A. Такая операция на таком множестве приводит к очень простой группе.

Тернарная, кватернарная и другие n-арные операции

Кроме унарных и бинарных операций существуют операции с другими большими арностями. Их называют n-арными операциями или мультиарными. Такие операции в качестве групповых операций не используются.

Для n=3 операция называется тернарной, для n=4 будет кватернарная операция. И т.д.

Примерами тернарной операции являются функции от трех переменных: y=f(x₁,x₂,x₃). Или, например, смешанное произведение трех трехмерных векторов: (A,B,C) = (A·[BxC]), это скалярное произведение первого вектора на векторное произведение второго и третьего вектора.

Обратите внимание, что настоящая тернарная операция (да и любая n-арная операция с n>2) не должна сводиться к последовательному применению двух (и более) однотипных бинарных операций. Если мультиарная операция сводится к комбинации нескольких однотипных бинарных операций, то группа с такой операцией может существовать, но все три правила такой группы определяются именно для той бинарной операции, к которой сводится мультиарная операция.

Например, смешанное произведение трехмерных векторов нельзя свести к двум скалярным произведениям или к двум векторным произведениям. Поэтому смешанное произведение векторов является настоящей тернарной операцией и не используется в группах. Ещё примером настоящей тернарной операции (в общем случае) является операция, определенная на множестве функций, по взятию неопределенного интеграла от произведения трех функций:

А вот пример ненастоящей, а формальной тернарной операции. Рассмотрим функцию от трех аргументов:

Если ввести бинарную функцию

Тогда тернарную функцию можно переписать как

Таким образом, эта тернарная операция свелась к двум последовательным применениям бинарной операции одного типа. Поэтому можно придумать группу, между элементами которой действует данная тернарная операция. Но все три правила групповой операции будут относиться только к бинарной операции, из которой состоит эта тернарная операция.

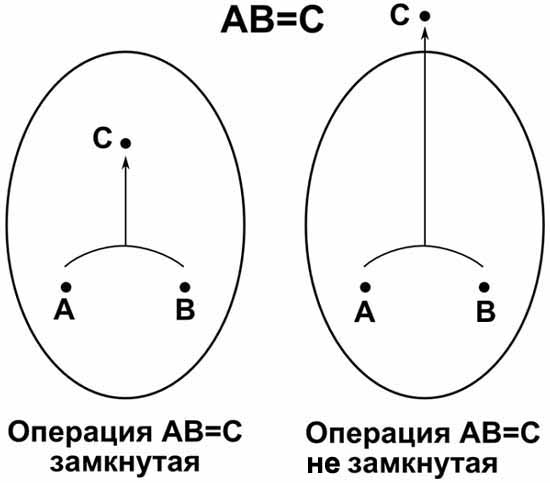
Замкнутая операция

Замкнутая операция, заданная между элементами множества, это такая операция, результатом которой являются элементы того же самого множества. Другими словами, применение замкнутой операции не «выбрасывает» её результат за пределы рассматриваемого множества.

Например, операция сложения для множества натуральных чисел, это замкнутая операция, так как при сложении двух натуральных чисел в результате всегда получается только натуральное число. А вот операция вычитания для множества натуральных чисел не является замкнутой, так как при вычитании большего натурального числа из меньшего получается отрицательное число, а не натуральное.

Аналогично, операция умножения на целых числах является замкнутой, так как при перемножении целых чисел всегда получается только целое число. А операция деления для множества целых чисел уже не является замкнутой, так как в результате деления целых чисел может получиться дробное число.

Векторное произведение трехмерных векторов является замкнутой операцией, так как в результате тоже получается трехмерный вектор. А вот скалярное произведение векторов, это уже не замкнутая операция, так как в результате такой операции получается не вектор, а число.

Замкнутые и незамкнутые операции бывают в операциях с любой мультиарностью.

Например, унарная операция транспонирования матрицы, это замкнутая операция, так как в результате транспонирования получается тоже матрица. А унарная операция получения определителя матрицы, это для матриц размера 2×2 и выше уже не замкнутая операция, так как в результате неё получается не матрица, а число.

Тернарная операция смешанного произведения трех трехмерных векторов не является замкнутой, так как в результате получается число, а не трехмерный вектор. А операция из предыдущего раздела, определенная для множества функций, по взятию неопределенного интеграла от произведения трех функций является замкнутой, так как в результате её тоже получается функция.

В качестве групповых операций используются только замкнутые операции.

Итак, все групповые операции, это только одновременно и замкнутые и бинарные операции.

Далее рассмотрим три обязательных групповых свойства этих групповых операций. Если эти три свойства не выполняются, то такое сочетание множества и операции на нем не является группой.

1. Ассоциативность

Свойство ассоциативности говорит о том, что для операций в группе скобки можно расставлять, как угодно (естественно, с соблюдением правила, что число открытых скобок должно быть равно числу закрытых скобок).

Например:
ABCDEFGH = (AB)(CD)(EFG)H = (ABC(DEFG))H = A(B(C(DE)F)G)H

Расстановка скобок определяется соображениями удобства. Понятно, что если скобки расставить вот так:
5677+(754-754)+(287-287)-5677,
то это выражение будет вычислено гораздо быстрее, чем, если скобки поставить, например, так:
(5677+754)+(-754+287)+(-287-5677)

2. Единичный элемент

В этом пункте определения группы нужно обратить внимание на то, что единичный (нейтральный) элемент группы всегда коммутирует с любым элементом множества: AE=EA, даже если группа некоммутативная.

Обратите внимание, что единичные элементы группы на одном и том же множестве могут быть разными для разных операций. Ведь это, по существу, разные группы. Например, для множества вещественных чисел операция сложения дает группу с единичным элементом равным 0. А операция умножения на том же множестве (без нуля, естественно) дает группу с единичным элементом равным 1.

Еще примеры единичных элементов группы. Если группу образуют матрицы размера nxm с операцией сложения матриц, то единичным элементом группы будет нулевая матрица размера nxm. Если группу образуют квадратные матрицы размера nxn с операцией умножения матриц, то единичным элементом группы будет матрица размера nxn, с единицами по диагонали и нулями во всех других местах.

Еще обратим внимание на то, что самая маленькая группа состоит только из одного элемента. И этим единственным элементом группы как раз и является единичный элемент. Именно в таких группах унарные замкнутые операции можно формально считать бинарными замкнутыми операциями. Выше был дан пример такой группы из одной симметричной матрицы с групповой операцией транспонирования матрицы.

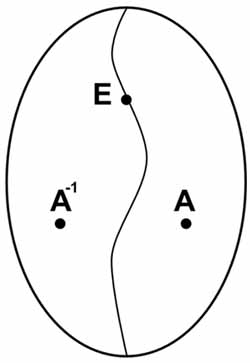
3. Обратный элемент

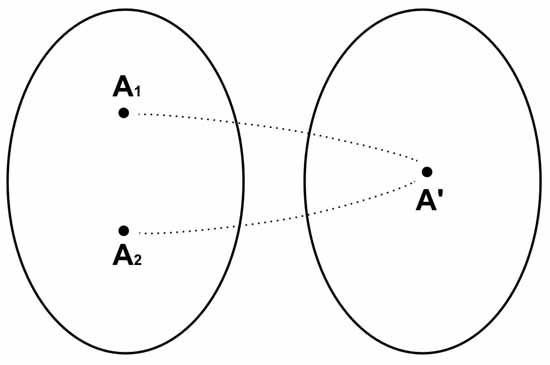
Следующее, на что надо обратить внимание, это то, что совсем необязательно, чтобы элемент группы не совпадал со своим обратным элементом. Иногда, начинающие знакомиться с теорией групп думают, что группа должна иметь такую структуру, как на рисунке. То есть, будто бы, любое групповое множество можно разделить на две части. В разных частях, будто бы, находятся элементы обратные друг другу, и есть еще один единичный элемент, который обратен самому себе в качестве исключения.

Такая ситуация действительно бывает, но не всегда. Примером того, когда бывает такая ситуация, служит группа с операцией сложения для множества целых чисел (или рациональных или вещественных чисел). В этом случае мы можем разделить множество элементов группы на три подмножества, в одном из которых будут все положительные числа, а в другом подмножестве будут все отрицательные числа. И еще будет третье подмножество, состоящее только из одного числа 0, которое является единичным элементом группы.

Такое разделение в этом примере неоднозначное. В первое подмножество мы можем включить все отрицательные числа, кроме, например, числа (-2). Вместо него включим в первое подмножество число (+2). А во второе подмножество включаем все положительные числа, кроме числа (+2), вместо которого берем число (-2).

Например, группа отражений трехмерного пространства относительно плоскости с операцией последовательного применения двух отражений. Это группа из двух элементов. Первый элемент, это единичный элемент, когда пространство не преобразуется. Второй элемент, это отражение. При отражении каждая точка пространства переходят в точку, расположенную на прямой линии, перпендикулярной плоскости, и на таком же расстоянии от плоскости, только с другой стороны этой плоскости. Если сделать два таких последовательных отражения, то точки пространства вернутся на свои первоначальные места, то есть получим единичный элемент группы. Значит, отражение является обратным элементом группы к самому себе.

Еще пример, когда обратный элемент группы совпадает со своим элементом, это группа перестановок. Если 2 раза сделать одну и ту же перестановку, то ничего не изменится.

Подгруппа

Понятие подгруппы более сложное, чем понятие подмножества. Не любое подмножество группового множества может образовать подгруппу.

В группе и в её подгруппе действует одна и та же групповая операция. Значит, чтобы выделить подгруппу из группы, надо в групповом множестве выделить такое подмножеств, чтобы это подмножество с этой операцией само образовывало самостоятельную группу.

Понятно, что раз в подгруппе действует та же самая групповая операция, то значит, в подгруппу всегда входит единичный элемент группы. Бывает, что в одной группе можно найти несколько подгрупп, но каждая из этих подгрупп обязательно будет содержать единичный элемент группы.

У каждой группы, в общем случае, всегда есть две её тривиальных подгруппы. Это подгруппа с одним единичным элементом и подгруппа, которая совпадает с самой группой. Эти две подгруппы любой группы называются несобственными или тривиальными подгруппами. Если группа состоит только из одного элемента, то у неё только одна несобственная подгруппа.

Все другие подгруппы называются собственными (нетривиальными) подгруппами. Бывают такие группы, которые содержат только тривиальные подгруппы. А бывают и такие, которые кроме тривиальных подгрупп содержат еще и собственные подгруппы.

Группы, у которых есть только тривиальные подгруппы, называются простыми группами. Это по аналогии с простыми числами. Простые числа, это такие числа, которые имеют только два своих делителя: число 1 и само себя.

Рассмотрим примеры групп, которые имеют собственные подгруппы.

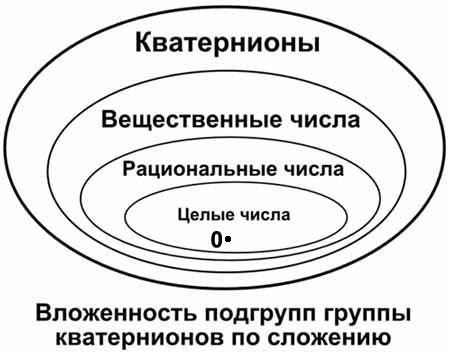
Группа для множества комплексных чисел с операцией сложения имеет в качестве подгруппы группу вещественных чисел с операцией сложения. В свою очередь группа вещественных чисел с операцией сложения имеет подгруппу в виде группы рациональных чисел. При этом группа рациональных чисел с операцией сложения является ещё и подгруппой комплексных чисел с операцией сложения. («Подгруппа моей подгруппы является моей подгруппой.»)

У группы рациональных чисел по сложению есть еще одна подгруппа, это группа целых чисел по сложению. Таким образом, группа целых чисел со сложением является ещё и подгруппой таких групп, как группа вещественных чисел и группа комплексных чисел.

А вот натуральные числа с операцией сложения уже не являются подгруппой группы целых чисел, так как множество натуральных чисел с операцией сложения не образуют группы. Операция сложения не является групповой операцией для множества натуральных чисел, так как для такого сочетания множества и операции не выполняется третье свойство группы, о существовании обратных элементов. (А в России и в Германии не выполняется ещё и второе свойство группы, так как в этих странах число 0 не считается натуральным числом.)

Если в какой-то группе есть две подгруппы, то их пересечение всегда тоже является подгруппой данной группы. А вот объединение этих подгрупп не всегда является подгруппой данной группы.

Изоморфизм и гомоморфизм

Гомоморфизм

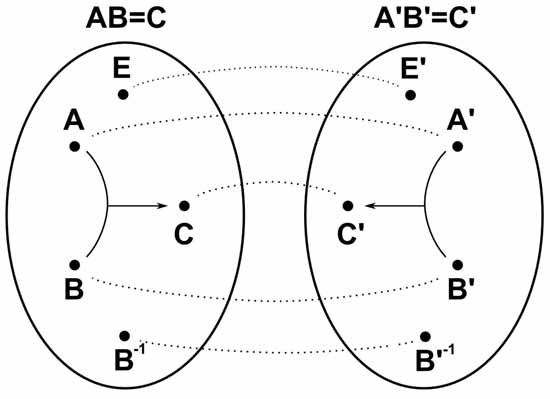
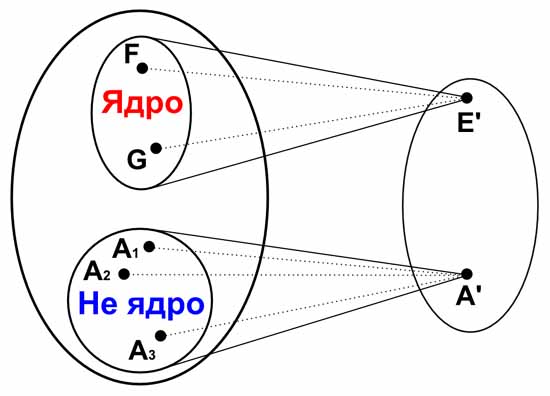
Одна группа гомоморфна другой группе, если любым двум элементам A и B из первой группы можно однозначно сопоставить два элемента A’ и B’, соответственно, из второй группы так, что если AB=C, а A’B’=C’, то элементу C из первой группы однозначно сопоставляется элемент C’ из второй группы.

Фактически, это означает, что существует какая-то однозначная операция отображения всех элементов первой группы на все элементы второй группы так, что при этом сохраняются все отношения между элементами, задаваемые групповыми операциями. Такое отображение называется гомоморфизмом.

Из этого понятно, что единичный элемент первой группы при гомоморфизме всегда соответствует единичному элементу второй группы. А все пары взаимно обратных элементов первой группы всегда соответствуют парам взаимно обратных элементов второй группы.

Простой пример гомоморфизма. Группу целых четных чисел с операцией сложения можно однозначно отобразить на группу всех целых чисел с операцией умножения. При этом числу 0 первой группы соответствует число 0 второй группы. Числу 2 первой группы соответствует число 1 второй группы. Числу 4 первой группы соответствует число 2 второй группы. И т.д. То же самое и с отрицательными числами. В общем случае число n из второй группы является соответствием числа 2n из первой группы.

Гомоморфизм требует однозначности такого отображения, но не требует при этом взаимности этого отображения. То есть элемент A из первой группы имеет только один соответствующий ему элемент A’ из второй группы. Во второй группе нет никакого другого элемента, который соответствует элементу A из первой группы. Но вот для двух разных элементов A₁ и A₂ из первой группы (A₁≠A₂) допускается иметь только один соответствующий им элемент A’ из второй группы.

В этом смысле вторая группа может не только иметь меньше элементов, чем первая группа, но и быть более простой, чем первая группа. Ядром гомоморфизма первой группы называется такая подгруппа первой группы, которая при гомоморфизме переходит в единичный элемент второй группы.

Изоморфизм

Изоморфизм, это взаимно однозначный гомоморфизм.

То есть, когда элементу A первой группы не только соответствует один элемент A’ второй группы, но и элементу A’ соответствует только один элемент A из первой группы.

Если между двумя группами существует изоморфизм, то данные группы называются изоморфными. Изоморфные группы не отличаются друг от друга с точки зрения теории групп. С точки зрения теории групп изоморфные группы являются совершенно одинаковыми. Элементы таких групп могут иметь разную математическую природу, операции таких групп также могут быть разными, но в теории групп, это одна и та же группа.

Рассмотрим пример изоморфизма. Пусть одна группа представляет собой 4 числа, 1, i, -1, -i, где i, это мнимая единица, а групповой операцией будет умножение этих чисел. Данная группа изоморфна группе вращений плоскости, которые совмещают квадрат с самим собой при поворотах квадрата вокруг своего центра с групповой операцией последовательного применения двух вращений.

Соответствуют друг другу число 1 и поворот на 0 градусов, число i и поворот на 90 градусов, число (-1) и поворот на 180 градусов, число (-i) и поворот на 270 градусов. Можно убедиться, что операция умножения в первой группе точно соответствует операции сочетания двух соответствующих поворотов из второй группы.

Изоморфизм в теории групп полезен тем, что позволяет перенести многие доказанные математиками вещи из одной области математики в другую, когда удается доказать изоморфизм основных групп в этих разных областях математики.

Источник