Что такое евклидово пространство
Евклидово пространство
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно 


1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство 

в простейшем случае (евклидова норма):
где 
2. Метрическое пространство, соответствующее пространству описанному выше. То есть 

где 

Содержание
Связанные определения
Примеры
Наглядными примерами евклидовых пространств могут служить пространства:
Более абстрактный пример:
Вариации и обобщения
См. также
Ссылки
Полезное
Смотреть что такое «Евклидово пространство» в других словарях:
ЕВКЛИДОВО ПРОСТРАНСТВО — конечномерное векторное пространство с положительно определённым скалярным произведением. Является непосредств. обобщением обычного трёхмерного пространства. В Е. п. существуют декартовы координаты, в к рых скалярное произведение ( ху )векторов х … Физическая энциклопедия
ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называется n мерное векторное пространство, в котором определено скалярное произведение … Большой Энциклопедический словарь
Евклидово пространство — пространство, свойства которого описываются аксиомами евклидовой геометрии. Упрощенно можно определить евклидово пространство, как пространство на плоскости или в трехмерном объеме, в которых заданы прямоугольные (декартовы) координаты, а… … Начала современного естествознания
Евклидово пространство — [Euclidean space] см. Многомерное (n мерное) векторное пространство, Векторное (линейное) пространство … Экономико-математический словарь
евклидово пространство — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN Cartesian space … Справочник технического переводчика
евклидово пространство — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называют n мерное векторное пространство, в котором определено скалярное произведение. * * * ЕВКЛИДОВО ПРОСТРАНСТВО ЕВКЛИДОВО… … Энциклопедический словарь
ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого изучаются в евклидовой геометрии. В более широком понимании Е. п. наз. n мерное векторное пространство, в к ром определено скалярное произведение … Естествознание. Энциклопедический словарь
ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. конечномерное действительное векторное пространствоRn со скалярным произведением( х, у), х, к рое в надлежащим образом выбранных координатах… … Математическая энциклопедия
Евклидово пространство — (в математике) пространство, свойства которого описываются аксиомами евклидовой геометрии (См. Евклидова геометрия). В более общем смысле Е. п. называется n мepное Векторное пространство, в котором возможно ввести некоторые специальные… … Большая советская энциклопедия
Что такое Евклидово пространство?
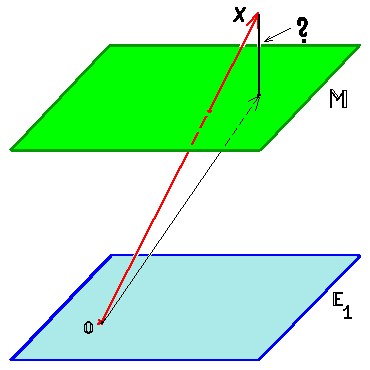
Если заглянуть в справочники или энциклопедии, то можно найти следующий ответ на сформулированный выше вопрос: «Евклидово пространство – в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии» [1].
Действительно, в АКСИОМЕ 9 Евклид упоминает вскользь слово «пространство» [2]: «И две прямые не содержат пространства».
Фактически же, здесь, как и в во всех прочих аксиомах, речь идёт не о пространстве, а о плоскости, которая является лишь слоем пространства, толщиной в одну точку. Туманную формулировку 9-й аксиомы можно интерпретировать следующим образом [3]: «два отрезка не могут сходиться в двух различных точках – то есть ограничивать некоторую фигуру конечной площади» (см. рисунок слева).
Примечательно, что это единственное (!) упоминание слова «пространство» Евклидом. Больше мы не встретим даже намёка на пространство ни среди других аксиом, ни среди постулатов, ни среди определений его 15-томного труда.
Таким образом, согласно энциклопедиям, ЕВКЛИДОВО ПРОСТРАНСТВО (в изначальном смысле) – это плоскость, которую не содержат две прямые. 🙂
P.S. Из правого рисунка видно, что так называемые «пространства» Евклида, Лобачевского или Римана на самом деле являются лишь поверхностями с разными геометрическими свойствами.
1. Евклидово пространство: Материал из Википедии. – https://ru.wikipedia.org/wiki/Евклидово_пространство
2. Начала Евклида. Книги I-XV. Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при участии М. Я. Выгодского и И. Н. Веселовского. – Гос. изд-во технико-теоретич. лит-ры, М.-Л.: 1950. – 1299 с.
Евклидовы пространства
Определение евклидова пространства
0\quad \forall \mathbf
\forall \lambda\in \mathbb
Линейные операции над векторами евклидова пространства удовлетворяют аксиомам 1–8 линейного пространства, а операция скалярного умножения векторов удовлетворяет аксиомам 1–4 скалярного произведения. Можно сказать, что евклидово пространство — это вещественное линейное пространство со скалярным произведением. Поскольку евклидово пространство является линейным пространством, на него переносятся все понятия, определенные для линейного пространства, в частности, понятия размерности и базиса.
Простейшие следствия из аксиом скалярного произведения
1. Аксиомы 2 и 3 скалярного произведения можно заменить одним условием линейности скалярного произведения по первому сомножителю:
\forall \alpha,\beta\in \mathbb
2. Условие линейности скалярного произведения по первому сомножителю в силу симметричности (аксиома 1) справедливо и для второго сомножителя, т.е. скалярное произведение линейно по любому сомножителю.
3. Линейность скалярного произведения по любому сомножителю распространяется на линейные комбинации векторов:
для любых векторов [math]\mathbf_i,\,\mathbf
4. Если хотя бы один сомножитель — нулевой вектор, то скалярное про изведение равно нулю:
Неравенство Коши-Буняковского
Для любых векторов [math]\mathbf[/math] и [math]\mathbf
В самом деле, для любого действительного числа [math]\lambda[/math] и любых векторов [math]\mathbf[/math] и [math]\mathbf
Примеры евклидовых пространств
Определяя для элементов линейного пространства операцию скалярного произведения, получаем евклидово пространство. Если скалярное произведение можно ввести разными способами в одном и том же линейном пространстве, то и получаемые евклидовы пространства будут разными. Приведем примеры евклидовых пространств, соответствующих рассмотренным ранее примерам линейных пространств.
3. В пространстве [math]\mathbb
Значит, выполняются аксиомы 2 и 3. Аксиома 4 также выполняется, так как квадратичная форма [math]\langle x,x\rangle= x^TAx[/math] положительно определенная. Таким образом, пространство [math]\mathbb
Приведем примеры формул, которые не задают скалярного произведения в [math]\mathbb
1) [math]\langle x,y\rangle= |x_1|\cdot|y_1|+|x_2|\cdot|y_2|[/math] — аксиомы 1, 4 выполняются, а аксиомы 2, 3 — нет;
2) [math]\langle x,y\rangle=x_2\cdot y_2[/math] — аксиомы 1, 2, 3 выполняются, а аксиома 4 — нет.
4. Пространство [math]\
6. В пространстве [math]P(\mathbb
В пространстве [math]P_3(\mathbb
В силу симметричности и линейности правой части (8.30) по значениям многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выполнение аксиомы 4. Приравняв скалярный квадрат нулю, получаем
Длина вектора и угол между векторами в евклидовом пространстве
Углом между ненулевыми векторами [math]\mathbf[/math] и [math]\mathbf
Из неравенства Коши-Буняковского (8.25) следует неравенство треугольника :
то есть [math]|\mathbf+\mathbf
Пример 8.17. Даны векторы евклидовых пространств:
y=\begin
y=\begin
q(x)=x+2[/math] — элементы пространства [math]P_2(\mathbb
q(x)=x+2[/math] — элементы пространства [math]P_2(\mathbb
В каждом пространстве найти длины двух данных векторов и угол между ними.
Решение. а) Находим скалярные произведения:
б) Находим скалярные произведения:
в) Находим скалярные произведения:
г) Находим скалярные произведения:
\langle p,q\rangle= 1\!\cdot\!0+(-2)\!\cdot\!1+1\!\cdot\!2=0;
\langle q,q\rangle= 0\!\cdot\!0+1\!\cdot\!1+2\!\cdot\!2=5.[/math]
д) Находим скалярные произведения:
\langle p,q\rangle= 0\!\cdot\!3+1\!\cdot\!4+4\!\cdot\!5=24;
\langle q,q\rangle= 3\!\cdot\!3+4\!\cdot\!4+5\!\cdot\!5=50.[/math]
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Евклидово пространство
Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты. В настоящем разделе понятие расстояния между двумя векторами — элементами линейного пространства — будет вводиться посредством скалярного произведения векторов. Насколько обоснован такой порядок введения понятий:
Определения
Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:
Свойства
Теорема. Имеет место неравенство Коши–Буняковского:
С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:
Теорема. Имеет место неравенство треугольника
Пример. Найти расстояние между полиномами
Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной, имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если коэффициенты полиномов
Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден для наблюдения за большими объектами, а телескоп — за малыми.
Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.
Теорема. В евклидовом пространстве имеет место равенство параллелограмма
Ортогонализация
Чему равно расстояние между двумя векторами ортонормированного базиса?
Пример. Ортогонализовать систему векторов
Пример. Пусть в пространстве полиномов скалярное произведение задается формулой
Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.
Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.
Матричный формализм алгоритма Грама-Шмидта: QR-разложение
Пример. Для матрицы из предыдущего примера имеем:
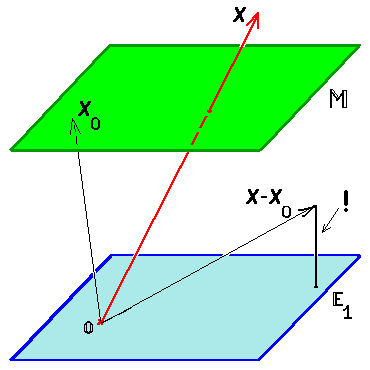
Расстояние от точки до многообразия
Пример. Множество
Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой
Вычисление расстояния
Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений ☞ ЗДЕСЬ.
Доказательство ☞ ЗДЕСЬ.
Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.
Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями) ☞ ЗДЕСЬ.
Угол между вектором и линейным многообразием
Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.
Свойства матрицы Грама
Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.
Доказательство ☞ ЗДЕСЬ
Матрица Грама линейно независимой системы векторов является положительно определенной. Матрица Грама произвольной системы векторов является положительно полуопределенной.
Дальнейшие свойства матрицы и определителя Грама ☞ ЗДЕСЬ
Задачи
Источник
Материалы этого раздела составлены на основе книги
Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969
Евклидово пространство
Во всех определениях евклидовы пространства состоят из точек, которые определяются только теми свойствами, которыми они должны обладать для формирования евклидова пространства.
Содержание
Определение [ править ]
История определения [ править ]
Евклидова геометрия не применялась в пространствах более чем трех измерений до 19 века. Людвиг Шлефли обобщил евклидову геометрию на пространства n измерений, используя как синтетические, так и алгебраические методы, и открыл все регулярные многогранники (многомерные аналоги Платоновых тел ), которые существуют в евклидовых пространствах любого числа измерений. [4]
Мотивация современного определения [ править ]
Техническое определение [ править ]
Евклидово пространство является аффинным пространством над переАльса таким образом, что ассоциированное векторное пространство является евклидовым векторным пространством. Евклидовы пространства иногда называют евклидовыми аффинными пространствами, чтобы отличить их от евклидовых векторных пространств. [6]
(Второй + в левой части является векторным сложением; все остальные + обозначают действие вектора на точку. Это обозначение не является двусмысленным, поскольку для различения двух значений + достаточно взглянуть на характер его левого аргумента.)
Как объяснялось ранее, некоторые из основных свойств евклидовых пространств являются результатом структуры аффинного пространства. Они описаны в § Аффинная структура и ее подразделы. Свойства, полученные в результате внутреннего продукта, объясняются в § Метрическая структура и ее подразделы.
Прототипные примеры [ править ]
Для любого векторного пространства сложение действует свободно и транзитивно в самом векторном пространстве. Таким образом, евклидово векторное пространство можно рассматривать как евклидово пространство, которое само ассоциируется с векторным пространством.
Аффинная структура [ править ]
Подпространства [ править ]
Евклидово векторное пространство (то есть такое евклидово пространство ) имеет два вида подпространств: его евклидовы подпространства и его линейные подпространства. Линейные подпространства являются евклидовыми подпространствами, а евклидово подпространство является линейным подпространством тогда и только тогда, когда оно содержит нулевой вектор. E = E → <\displaystyle E=<\overrightarrow
Линии и сегменты [ править ]
Отсюда следует, что есть ровно одна линия, которая проходит через две различные точки (содержит). Это означает, что две различные прямые пересекаются не более чем в одной точке.
Более симметричное представление прямой, проходящей через P и Q :
В евклидовом векторном пространстве нулевой вектор обычно выбирается за O ; это позволяет упростить предыдущую формулу до
Параллелизм [ править ]
Два подпространства S и T одной размерности в евклидовом пространстве параллельны, если они имеют одинаковое направление. [a] Эквивалентно, они параллельны, если есть вектор сдвига v, который отображает один в другой:
Отсюда следует, что в евклидовой плоскости две прямые либо пересекаются в одной точке, либо параллельны.
Концепция параллельных подпространств была расширена на подпространства разных размеров: два подпространства параллельны, если направление одного из них совпадает с направлением на другое.
Метрическая структура [ править ]
Евклидова норма вектора х является
Расстояние и длина [ править ]
Ортогональность [ править ]
Два линейных подпространства ортогональны, если каждый ненулевой вектор первого перпендикулярен каждому ненулевому вектору второго. Отсюда следует, что пересечение линейного подпространства сводится к нулевому вектору. E → <\displaystyle <\overrightarrow
Два сегмента AB и AC, которые имеют общую конечную точку, перпендикулярны или образуют прямой угол, если векторы и ортогональны. A B → <\displaystyle <\overrightarrow 
Если AB и AC образуют прямой угол, то
Угол [ править ]
(Неориентированный) угол θ между двумя ненулевыми векторами x и y в равен E → <\displaystyle <\overrightarrow
θ = arccos ( x ⋅ y ‖ x ‖ ‖ y ‖ ) <\displaystyle \theta =\arccos \left(<\frac
Декартовы координаты [ править ]
Другие координаты [ править ]
Аффинное базис евклидова пространства размерности п представляет собой набор п + 1 точек, которые не содержатся в гиперплоскости. Аффинный базис определяет барицентрические координаты для каждой точки.
Изометрии [ править ]
Изометрия между двумя метрическими пространствами является взаимно однозначным соответствием с сохранением расстояния, [Ь] то есть
В случае евклидова векторного пространства изометрия, которая отображает начало координат в начало координат, сохраняет норму
f ( P ) = O ′ + f → ( O P → ) <\displaystyle f(P)=O'+<\overrightarrow
является изометрией евклидовых пространств.
Из предыдущих результатов следует, что изометрия евклидовых пространств отображает прямые в прямые и, в более общем смысле, евклидовы подпространства в евклидовы подпространства той же размерности, и что ограничение изометрии на эти подпространства является изометриями этих подпространств.
Изометрия с прототипными примерами [ править ]
которое является изометрией евклидовых пространств. Обратная изометрия
Это означает, что с точностью до изоморфизма существует ровно одно евклидово пространство заданной размерности.
Евклидова группа [ править ]
Они находятся в биективном соответствии с векторами. Это причина того, что пространство переводов называют векторным пространством, связанным с евклидовым пространством. Переводы образуют нормальную подгруппу евклидовой группы.