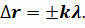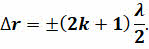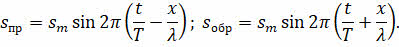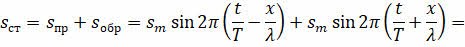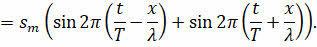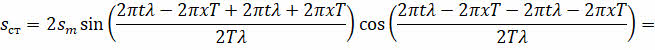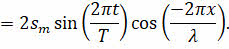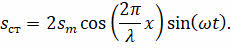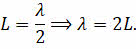Что такое дифференциация волн
Дифракция волн
Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный) — явление, которое можно рассматривать как отклонение от законов геометрической оптики при распространении волн. Первоначально понятие дифракции относилось только к огибанию волнами препятствий, но в современном, более широком толковании, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн в неоднородных средах, а также при распространении ограниченных в пространстве волн. Дифракция тесно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как частный случай интерференции (интерференция вторичных волн).
Дифракция волн наблюдается независимо от их природы и может проявляться:
Дифракционные эффекты зависят от соотношения между длиной волны и характерным размером неоднородностей среды либо неоднородностей структуры самой волны. Наиболее сильно они проявляются при размерах неоднородностей сравнимых с длиной волны. При размерах неоднородностей существенно превышающих длину волны (на 3-4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае вместо дифракции часто говорят о явлении рассеяния волн.
Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).
Содержание
Тонкости в толковании термина «дифракция»
В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её. Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление, не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка). Исходное ограничение волнового поля в пространстве и его определенная структура могут возникнуть не только за счет присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции. Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в ее поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции. Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия. Такова, например, дифракция на непоглощающих (прозрачных) так называемых фазовых структурах.
С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным.
Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то часто под дифракцией понимают проявление любого отступления от законов геометрической оптики. При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является. Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу. Еще один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Общим свойством всех эффектов дифракции является именно определенная зависимость данного явления от соотношения между длиной волны и размером неоднородностей среды. Поэтому дифракция представляет собой универсальное волновое явление и характеризуется одними и теми же законами в случае волн разной природы.
Дифракция волн.
Дифракция волн (от лат. diffractus — разломанный) — в первоначальном узком смысле — огибание волнами препятствий, в современном — более широком — любые отклонения при распространении волн от законов геометрической оптики.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
Способность волн огибать препятствия можно наблюдать на морских волнах, легко огибающих камень, размеры которого малы по сравнению с длиной волны. Звуковые волны также способны огибать препятствия, благодаря чему мы слышим, например, сигнал машины, находящейся за углом дома.
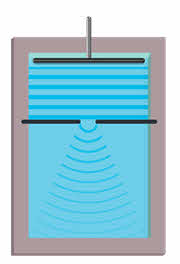
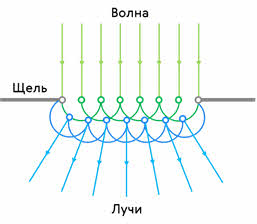
Явление дифракции волн на поверхности воды можно наблюдать, если поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны.
За экраном распространяется круговая волна, как если бы в отверстии экрана располагалось колеблющееся тело — источник волн. Согласно принципу Гюйгенса-Френеля, так и должно быть. Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.
Если размеры щели велики по сравнению с длиной волны, то волна проходит сквозь щель, почти не меняя своей формы, лишь по краям видны еле заметные искривления волновой поверхности, благодаря которым волна проникает и в пространство за экраном.
Дифракция волн. Принцип Гюйгенса-Френеля. Примеры дифракции волн
Явление дифракции волн
Как известно, любая волна, будь то свет, звук или возмущения на поверхности воды, в гомогенной среде распространяется вдоль прямой траектории.
Представим себе волновой фронт, который имеет плоскую поверхность и движется в некотором направлении. Что будет, если на пути этого фронта возникнет препятствие? Препятствием может служить что угодно (камень, здание, узкая щель и так далее). Оказывается, что после прохождения препятствия волновой фронт уже не будет плоским, а примет более сложную форму. Так, в случае маленького круглого отверстия фронт волны, пройдя через него, становится сферическим.

Явление изменения направления распространения волны, когда она встречает на своем пути препятствие, получило название дифракции (diffractus с латинского означает «изломанный»).
Результатом этого явления является то, что волна проникает в пространство за препятствием, куда она бы никогда не попала при ее прямолинейном движении.
Пример дифракции волн на берегу моря показан на рисунке ниже.

Условия наблюдения дифракции
Описанный выше эффект излома волны при прохождении препятствия зависит от двух факторов:
При каком условии наблюдается дифракция волн? Для лучшего понимания ответа на этот вопрос следует отметить, что рассматриваемое явление происходит всегда, когда волна наталкивается на препятствие, однако заметным оно становится только тогда, когда длина волны оказывается порядка геометрических параметров препятствия. Поскольку длины волн света и звука невелики по сравнению с размерами окружающих нас объектов, то и сама дифракция проявляется лишь в некоторых специальных случаях.
Почему происходит дифракция волн? Это можно понять, если рассмотреть принцип Гюйгенса-Френеля.
Принцип Гюйгенса
Рассматривая волновой сферический фронт, созданный точечным источником света, Гюйгенс пришел к следующему выводу: в процессе движения фронт проходит через ряд пространственных точек в эфире. Как только он их достигает, то заставляет колебаться. Колеблющиеся точки, в свою очередь, генерируют новое поколение волн, которые Гюйгенс назвал вторичными. От каждой точки вторичная волна является сферической, однако одна она не определяет поверхность нового фронта. Последняя является результатом наложения всех сферических вторичных волн.
Описанный выше эффект называется принципом Гюйгенса. Дифракцию волн он не объясняет (когда ученый его формулировал, о дифракции света еще не знали), однако такие эффекты, как отражение и преломление света, он описывает с успехом.
Поскольку корпускулярная теория света, выдвинутая Ньютоном, восторжествовала в XVII веке, о работах Гюйгенса забыли на 150 лет.
Томас Юнг, Огюстен Френель и возрождение принципа Гюйгенса
Явление дифракции и интерференции света было открыто в 1801 году Томасом Юнгом. Проводя эксперименты с двумя щелями, через которые проходил монохроматический световой фронт, ученый получил на экране картину из чередующихся темных и светлых полос. Юнг полностью объяснил результаты своих опытов, ссылаясь на волновую природу света, и подтверждая тем самым теоретические расчеты Максвелла.
Как только корпускулярная ньютоновская теория света была опровергнута опытами Юнга, французский ученый Огюстен Френель вспомнил про работы Гюйгенса и использовал его принцип для объяснения явления дифракции.
Френель полагал, что если электромагнитная волна, распространяясь прямолинейно, встречает препятствие, то часть ее энергии теряется. Остальная же часть расходуется на образование вторичных волн. Последние и приводят к возникновению нового волнового фронта, направление распространения которого отличается от исходного.
Описанный эффект, который не принимает во внимание эфир при генерации вторичных волн, получил название принципа Гюйгенса-Френеля. Дифракцию волн он описывает успешно. Более того, в настоящее время этот принцип используют для определения энергетических потерь при распространении электромагнитных волн, на пути которых встречается препятствие.
Дифракция на узкой щели
Теория построения дифракционных картин является достаточно сложной с математической точки зрения, поскольку предполагает решение уравнений Максвелла для электромагнитных волн. Тем не менее, принцип Гюйгенса-Френеля, а также ряд других приближений позволяют получать математические формулы, пригодные для практического их применения.
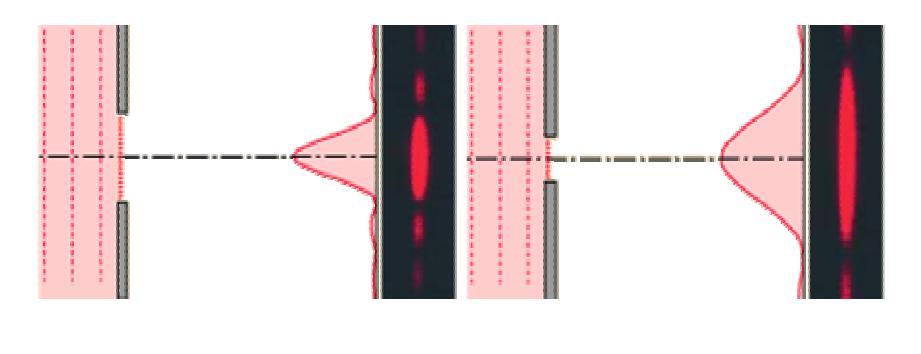
Если рассматривать дифракцию на тонкой щели, на которую падает параллельно плоский волновой фронт, то на экране, расположенном далеко от щели, появятся яркие и темные полосы. Минимумы дифракционной картины в этом случае описываются следующей формулой:
Из выражения следует, что центральный максимум будет более расплывчатым, если уменьшить ширину щели и увеличить длину световой волны. Рисунок ниже показывает, как будет выглядеть соответствующая дифракционная картина.
Дифракционная решетка
Если на одну пластину нанести совокупность щелей из примера выше, то получится так называемая дифракционная решетка. Используя принцип Гюйгенса-Френеля, можно получить формулу для максимумов (яркие полосы), которые получаются при прохождении через решетку света. Формула выглядит так:
Здесь параметр d является расстоянием между ближайшими щелями на решетке. Чем меньше это расстояние, тем больше будет дистанция между яркими полосами на дифракционной картине.
Так как угол θ для максимумов m-го порядка зависит от длины волны λ, то при прохождении белого света через дифракционную решетку на экране появляются разноцветные полосы. Этот эффект используют при изготовлении спектроскопов, способных анализировать характеристики излучения или поглощения света тем или иным источником, например, звездами и галактиками.
Важность дифракции для оптических приборов
Одной из главных характеристик таких приборов, как телескоп или микроскоп, является их разрешающая способность. Под ней понимают минимальный угол, при наблюдении под которым еще различимы отдельные объекты. Этот угол определяется из анализа дифракции волн согласно критерию Рэлея по следующей формуле:
Если применить этот критерий к телескопу «Хаббл», то получим, что прибор на расстоянии 1000 световых лет способен различать два объекта, расстояние между которыми аналогично таковому между Солнцем и Ураном.
5.1. Общая структура волн дифференциации
Сравнительный анализ волн дифференциации всех трех рассмотренных циклов позволяет выделить некоторые их общие черты. При общей продолжительности волн дифференциации, составляющей около пяти веков, в каждой из этих волн можно выделить ряд фаз (периодов), различающихся по характеру протекающих в них процессов.
Вторая фаза волны дифференциации включает собственно геоэкономическую и геополитическую революцию, которые paдикально перекраивают экономическую и политическую карту мира; эта фаза имеет продолжительность около 200 лет. Для волны дифференциации первого (античного) цикла это был период между 600 и 400 гг. до н.э., когда в результате Великой греческой колонизации, персидских завоеваний, процессов, происходивших в Индии и Китае, тогдашний цивилизованный мир не только заметно расширился, но и качественно стал во многом другим. Центр политической, экономической, культурной жизни переместился из Египта, Ассирии и Вавилонии в Персию, Грецию, Китай, Индию. Именно на эту фазу геоэкономической и геополитической революции приходится пик «осевого времени» Ясперса, наиболее высокий взлет творческих исканий в области религии, философии, искусства: это время Будды, Заратуштры, Конфуция, Лао–цзы, Мо–цзы, Гераклита, Анаксагора, Сократа, Эсхила, Софокла, Эврипи–да, Фидия.
Для волны дифференциации второго (средневекового) цикла эта фаза приходится на период между 400 и 600 гг. н.э. — период Великого переселения народов, крушения Западной Римской империи, изменения ситуации во всем Средиземноморье и в прилегающих регионах, массовой миграции населения Китая на Юг, крупных сдвигов в Индии, связанных с образованием и крушением государства Гупт, нашествием гуннов–эфталитов и др.
Наконец, для волны дифференциации третьего цикла (Новое время) вторая фаза соответствует периоду между 1450 и 1650 гг., для которого наличие геоэкономической и геополитической революции вполне очевидно. Напомним, что это была эпоха Великих географических открытий, когда европейцами был открыт и начал осваиваться Новый Свет, были открыты новые морские и океанские пути в Африку и Азию, совершены первые кругосветные путешествия, а Московская Русь начала покорять и осваивать Сибирь. В результате этой геоэкономической и геополитической революции мир стал действительно глобальным, произошло его стремительное расширение и радикальное изменение. Центр политической, экономической и культурной жизни переместился из Средиземноморья в Северо–Западную Европу, вместо прежних мировых империй центральную роль в экономике и политике стали играть сначала Испания, затем Франция, Голландия и Англия», В культурном плане эта эпоха была необычайно плодотворна, на нее пришлось творчество Эразма Роттердамского, Сандро Боттичелли, Леонардо да Винчи, Рафаэля, Микеланджело Буонарроти, Тициана, Альбрехта Дюрера, Николая Коперника, Галилео Га–лилея, Никколо Макиавелли, Томаса Мора, Мартина Лютера, Мигеля Сервантеса, Вильяма Шекспира, Джордано Бруно, Фрэнсиса Бэкона, Рене Декарта, Рубенса, Ван–Дейка, Рембрандта, ряда крупных китайских философов, индийских поэтов Кабира, Нанака, Тулси Даса — автора поэмы «Рамаяна» и др.
Третья фаза волны дифференциации представляет собой завершение геоэкономической и геополитической революции и зарождение новой мировой империи, которая станет гегемоном в первой фазе следующей волны интеграции; продолжительность этой фазы составляет около 100–150 лет (при этом последний 50–летний период волны дифференциации, во время которого происходит бурный рост новой мировой империи, является по существу переходным, его можно рассматривать и как конец волны дифференциации, и как начало последующей волны интеграции). В третьей фазе мир после крупных и радикальных изменений начинает развиваться более спокойно, хотя новый мировой порядок еще не оформился, и происходят немалые потрясения. Так, в третьей фазе волны дифференциации первого (античного) цикла (между 400 и 300 гг. до н.э.) развитие как бы временно стабилизируется, а затем в ее конце происходит крушение державы Ахеменидов и образование державы Александра Македонского с последующим распадом на ряд крупных эллинистических государств; в это же время начинает образовываться империя Маурьев в Индии. Античная культура и соответствующие формы социальной жизни как бы «выплескиваются» вовне и заполняют большую часть Ойкумены. В третьей фазе волны дифференциации второго (средневекового) цикла (между 600 и 700 гг. н.э.) происходит зарождение ислама и образование Арабского халифата; исламская культура и соответствующий образ жизни снова как бы «выплескиваются» далеко за пределы Аравии, где они возникли. Но параллельно идет и «выплескивание» христианской культуры вместе с начинающей формироваться социальной и политической организацией, которую постепенно начинают принимать германские и славянские племена. Наконец, в третьей фазе волны дифференциации третьего цикла (между 1650 и 1800 гг.) в результате образования торгово–колониальных систем (голландской, английской, французской и др.) европейский торгово–промышленный капитализм и европейская культура «выплескиваются» далеко за пределы Европы и охватывает почти весь мир.
Итак, в эпохи, соответствующие волнам дифференциации, мир стремительно расширяется, а мировой порядок при этом радикально изменяется в результате геоэкономической и геополитической революции.
Следует также отметить, что начало образования очередной великой империи, которое наблюдается в конце каждой волны дифференциации (державы Александра Македонского и эллинистических государств в первом цикле. Арабского халифата во втором цикле и Британской империи в третьем цикле) определяется! не только политическими, но во многом и экономическими причинами. При этом экономика и политика идут рука об руку и работают друг на друга. В случае образования державы Александра Македонского это хорошо выразил И. Дройзен, который писал следующее: «Одним из сильнейших ферментов слагавшейся заново жизни должно было быть громадное количество благородного металла, данное в руки Александра завоеванием Азии.
Образование Арабского халифата, как уже говорилось, также во многом было вызвано экономическими причинами — прежде всего стремлением арабов контролировать транзитные торговые пути не только в Аравии, но и на всем Ближнем Востоке. Наконец, образование огромной Британской империи в XVIII в. было непосредственно связано с контролем над мировой океанской торговлей и с накоплением огромных богатств, которые вскоре дали толчок промышленному перевороту и обеспечили промышленно–финансовую монополию Великобритании в мире. Таким образом, переход от волны дифференциации к волне интеграции в каждом цикле вызывался совокупным действием мощных экономических, политических, социальных и культурных факторов. Эти факторы, усиливая друг друга по принципу синхронизации, о котором шла речь в главе 1, вызывали глобальные изменения всего мирового порядка.
Интерференция, дифракция и поляризация механических волн
Урок 20. Физика 11 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Интерференция, дифракция и поляризация механических волн»
Очень часто в среде одновременно распространяется не одна, а несколько различных волн. Так, например, если мы бросим в воду два камня, образовав тем самым две круговые волны. Однако посмотрите, каждая волна проходит сквозь другую и ведёт себя в дальнейшем так, как будто другой волны совсем не существовало.
Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются одна на другую. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте своими гребнями, то в этом месте возмущение поверхности воды усиливается. Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.
Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются.
Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды, называется интерференцией.
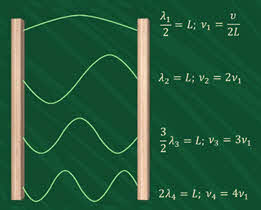
Выясним, при каких условиях наблюдается интерференция волн. Для этого будем непрерывно создавать волны на поверхности воды в двух каких-нибудь её точках. Для этого в непосредственной близости к поверхности воды поместим концы двух проволочек, приделанных к упругой металлической пластинке.
При колебании пластинки концы проволочек будут периодически погружаться в воду и возбуждать колебания, распространяющиеся в виде волн одинаковой длины по её поверхности. Каждая из проволочек возбуждает свою систему волн. Две системы волн, налагаясь одна на другую, будут взаимодействовать. В результате на поверхности воды возникает определённое, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.
Для дальнейшего важно, чтобы две системы волн были согласованы, то есть чтобы при одинаковой длине они выходили из центров колебания в одинаковых фазах. Такие волны называются когерентными.
В данном опыте когерентность обеспечена тем, что оба конца проволоки периодически касаются поверхности воды одновременно — волны оставляют центры колебания в одинаковых фазах.
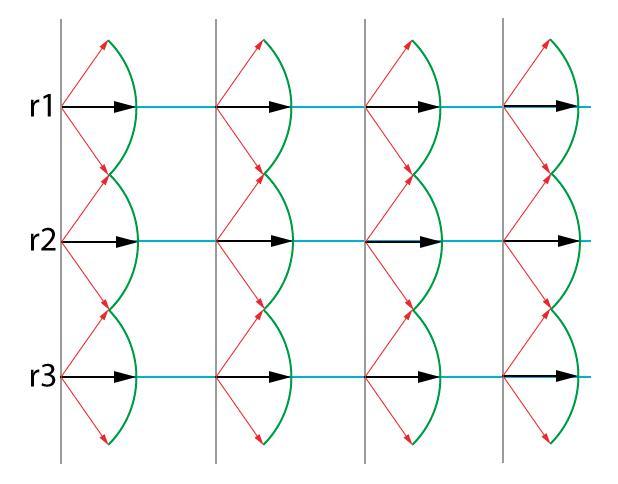
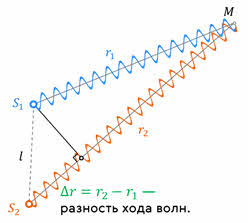
В любой точке на поверхности воды будут складываться колебания, вызванные двумя волнами. Однако результат сложения этих волн, приходящих в данную точку, зависит от разности фаз между ними. Для решения вопроса о том, в каких фазах встретятся в данной точке интерферирующие волны, нужно учесть разность хода этих волн. Пусть нас интересует результат наложения волн в точке, находящейся на расстоянии r1 от первого источника волн и на расстоянии r2 от второго источника.
Расстояние Δr = r2 – r1, называется разностью хода волн. Если источники волн колебались в одинаковых фазах, то при разности хода, равной целому числу длин волн или чётному числу полуволн, в данную точку волны будут приходить в одинаковых фазах и при сложении их в этой точке возникает усиление колебаний:
Если разность хода окажется равной нечётному числу полуволн, то волны от источников придут в эту точку в противоположных фазах и в ней произойдёт ослабление колебаний:
Когда мы с вами только начинали изучать волновое движение, мы говорили о том, что в процессе распространения волн происходит перенос энергии без переноса вещества. Возникает логичный вопрос, что происходит с этой энергией при гашении волн друг другом? Может быть, она превращается в другие формы, и в минимумах интерференционной картины выделяется тепло? Оказывается нет. Наличие минимума в данной точке интерференционной картины означает, что энергия сюда совсем не поступает. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счёт того, что в минимумы не поступает вовсе.
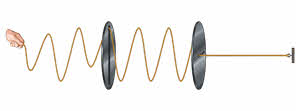
Ярким примером интерференции волн служит стоячая волна. Для её получения возьмём нить, один конец которой привязан к молоточку звонка, а к другому концу через блок подвешена маленькая гирька.
Частицы нити передают друг другу колебания от молоточка, и волна распространяется до блока, вызывая вынужденные колебания груза. Эти колебания порождают отражённую волну той же частоты. Таким образом, каждая точка нити участвует в двух колебаниях, которые приходят с разных сторон. Если изменять расстояние от молоточка до блока, то можно наблюдать, как при некоторых расстояниях возникают стоячие волны.
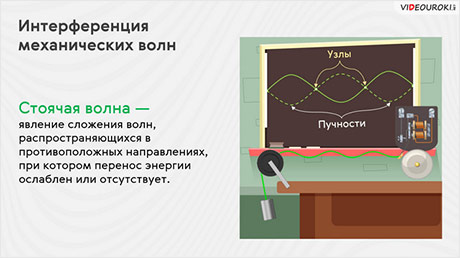
Стоячая волна — это вид волнового движения, происходящий без переноса энергии.
Такое название возникло потому, что при распространении таких волн нет перемещения фазы между колеблющимися точками, а некоторые из точек стоячей волны совсем не колеблются. Точки стоячей волны, которые не колеблются, называются узлами. Расстояние между соседними узлами составляет половину длины стоячей волны. А точки стоячей волны, амплитуды которых максимальны, называются пучностями.
Запишем уравнения прямой и обратной волны:
При наложении происходит сложение этих волн:
Упростим полученное выражение, вынеся общий множитель за скобки.
Далее воспользуемся формулой суммы синусов, знакомой вам из математики:
В силу чётности функции косинуса, а также помня о том, что отношение 2π/Т — это циклическая частота, получим уравнение стоячей волны:
Из него видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и во встречных волнах. А амплитуда колебаний при возбуждении стоячей волны зависит от положения колеблющейся точки, то есть определяет амплитуду колебаний в некоторой точке с координатой х.
В точках, находящихся на расстоянии целого числа длин полуволн, колебания происходят с удвоенной амплитудой, то есть наблюдаются интерференционные максимумы или пучности стоячей волны.
В точках же, находящихся на расстоянии нечётного числа четвертей волн, колебания вовсе не происходят. Здесь мы наблюдаем интерференционный минимум или узел.
В таблице приведено сравнение стоячей и бегущей волн:
Рассмотрим возбуждение стоячей волны в струне, закреплённой с двух концов. Очевидно, что точки закрепления будут являться узлами стоячей волны. Самая большая длина волны, возбуждаемая в струне, будет при условии, что её длина равна половине длины волны:
Такая длина волны соответствует самой низкой частоте, то есть основному музыкальному тону. Увеличивая частоту в целое число раз, мы можем получить первый, второй и так далее обертоны.
Частоты, при которых возникают стоячие волны, называются собственными или резонансными частотами.
Теперь давайте возьмём две одинаковые струны и поместим их на некотором расстоянии друг от друга одна под одной. Заставив нижнюю струну колебаться, мы заметим, как верхняя струна также начинает звучать. Это явление получило название акустического резонанса.
Таким образом, акустическим резонансом называется явление возрастания амплитуды звуковой волны в системе при приближении частоты источника, возбуждающего в ней колебания, к собственной частоте колебаний системы.
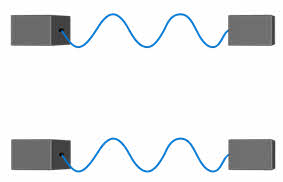
Теперь давайте проведём такой опыт. Получим в ванне на поверхности воды систему волн и ограничим их дальнейшее распространение отверстием, ширина которого в несколько раз больше длины волны. Не трудно увидеть, что за отверстием волны распространяются в области, ограниченной прямыми линиями, перпендикулярными к поверхности падающих волн. Только на сравнительно большом расстоянии от отверстия волны, слегка загибаясь, заходят за эти прямые.
Сузим ограничивающее отверстие до размера, меньшего длины волны падающих волн. Область за отверстием окажется заполненной круговыми волнами, как если бы в отверстии экрана находился источник волн — наблюдается дифракция волн.
Дифракцией называется явление огибания волнами препятствий, соизмеримых с длиной волны.
Это можно объяснить принципом Гюйгенса. Согласно ему каждая точка фронта (поверхности, достигнутой волной) является вторичным (то есть новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.
Явление дифракции, как и явление интерференции, присуще любому волновому процессу.
И рассмотрим ещё одно явление. Возьмём шнур, один конец которого прикрепим к стене. Возьмём верёвку, один конец которой закрепим к стене, и будем рукой создавать в ней колебания. Возбуждая колебания в шнуре мы видим, что колебания шнура происходят с разными амплитудами и в разных направлениях. Однако если его пропустить через узкую щель, то такая щель будет выделять из волны единственное направление колебаний, параллельное щели.
Теперь поставим на пути волны второй поляризатор с такой же щелью. Волна, выйдя из первой щели, свободно проходит через вторую, когда они параллельны. Если же повернуть вторую щель, перпендикулярно первой, то волна полностью гасится. Такую волну называют плоскополяризованной. То есть волна называется плоскополяризованной, если колебания во всех её точках происходят только в одной плоскости.
Прибор, превращающий неполяризованную волну в поляризованную, называют поляризатором. А прибор, позволяющий установить, поляризована или нет проходящая через него волна — анализатором.
Очевидно, что поляризация может происходить только в случае поперечных волн. Продольная волна не поляризуется.
Для закрепления материала решим с вами задачу. Разность хода двух когерентных волн с одинаковыми амплитудами равна 12 см, а длина волны — 8 см. Каков результат интерференции волн?