Что такое диагональное сечение
Что такое диагональное сечение
Диагональное сечение параллелепипеда – это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Это сечение всегда представляет собой прямоугольник или квадрат.
Диагональное сечение разбивает параллелепипед на две призмы
Диагональным сечением пирамиды называется сечение её плоскостью, проходящей через два боковых ребра пирамиды, не лежащих в одной грани.
Это сечение всегда представляет собой треугольник.
Любое диагональное сечение разбивает пирамиду на две пирамиды..
Осевое сечение фигуры – это сечение, которое проходит через ось фигуры и перпендикулярно основанию.
Осевое сечение конуса – это всегда равнобедренный треугольник.
Осевое сечение усеченного конуса – равнобедренная трапеция
Осевое сечение цилиндра – прямоугольник. Любое сечение, параллельное осевому – тоже прямоугольник.
3. Сечения плоскостью, параллельной основанию
3.1. Сечение цилиндра плоскостью, параллельной его основаниям
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
3.2. Сечение конуса плоскостью, параллельной его основанию
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковая поверхность – по окружности с центром на оси конуса.
О – Центр шара, В – центр круга сечения.
Самое большой сечение шара – сечение, проходящее через его центр
Что такое призма: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение призмы
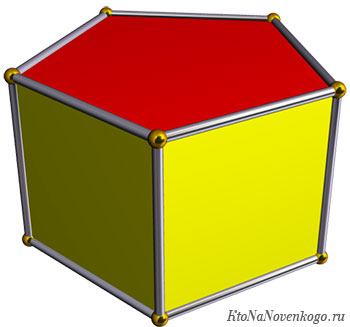
Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.
На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.
Элементы призмы
Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:
Примечание: свойства призмы представлены в отдельной публикации.
Варианты сечения призмы
Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.
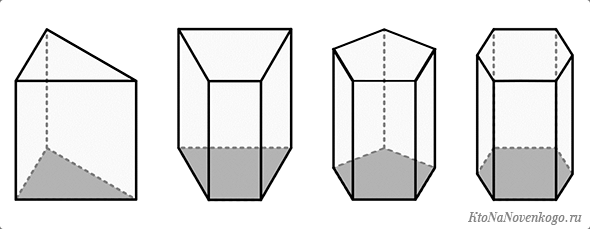
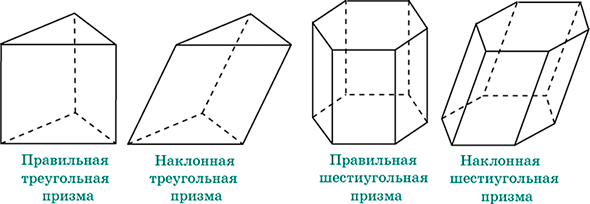
Виды призм
Рассмотрим разновидности фигуры с треугольным основанием.
Правильная четырехугольная призма
Элементы правильной четырехугольной призмы
Свойства правильной четырехугольной призмы
Формулы для правильной четырехугольной призмы
Указания к решению задач
При решении задач на тему «правильная четырехугольная призма» подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Задача.
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 ) 2 + 14 2 ) = 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a 2 + a 2 = 5 2
2a 2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h 2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
Что такое пирамида: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение пирамиды
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Что такое призма — определение и разновидности призм
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем о такой интересной геометрической фигуре, как ПРИЗМА.
Школьники сталкиваются с ней на уроках геометрии только в 10 классе. Соответственно, те, кто решил уйти после 9-го класса в колледж, этих знаний лишены. И мы восполним этот пробел.
А старшеклассникам наша статья (очень на это надеемся) поможет при подготовке к сдаче ЕГЭ. На экзаменах по математике попадаются несколько вопросов, связанных с ПРИЗМАМИ.
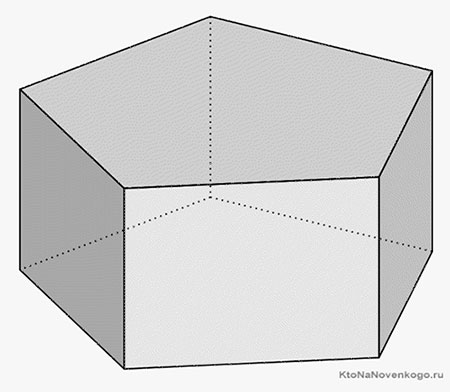
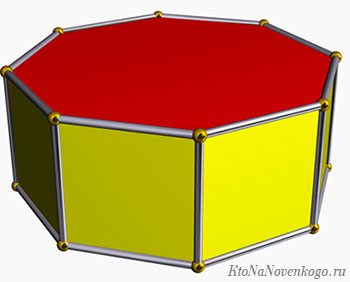
Призма – это геометрическая фигура, которая представляет собой объемный многогранник. Две его стороны лежат на параллельных основаниях и представляют собой различные многоугольники. А боковые грани – это параллелограммы, которые соединяются с основаниями.
Выглядит классическая призма так, как показано на рисунке выше.
На этом рисунке четко видны все элементы призмы:
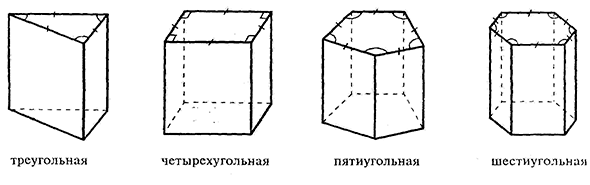
В зависимости от вида основания призмы бывают:
Разнообразие призм можно считать бесконечным. Могут быть фигуры, у которых в основании и 10-угольник, и 20-угольник, и даже 100-угольник. Но, к счастью, такие фигуры попадаются крайне редко. И их точно не изучают в школе.
История изучения призмы
О существовании призм знали еще в Древнем Египте и Древнем Вавилоне. Об этом свидетельствуют различные археологические находки, прежде всего, остатки зданий и памятников.
Но научное описание призм – это заслуга древнегреческих математиков. В первую очередь, Аристотеля. Он даже целое направление науки придумал – стереометрией. В переводе с греческого это означает измерение пространства («метрио» — измерение, «стереос» — пространство).
И в рамках этой науки Аристотель занимался изучением призм, кубов, параллелепипедов и других объемных геометрических фигур.
Естественно, не обошел своим вниманием призмы и знаменитый древнегреческий математик и ученый – Евклид. В своих трудах он дает следующее описание:
Призма – это телесная (то есть пространственная) фигура, которая заключена между несколькими плоскостями. Две из них параллельны друг другу, равны и противоположны. А другие в любом количестве представляют собой параллелограммы.
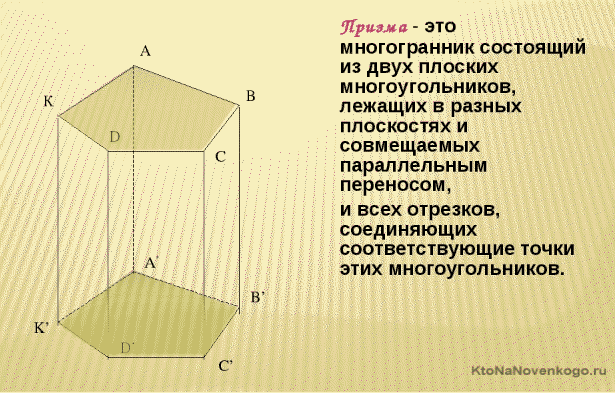
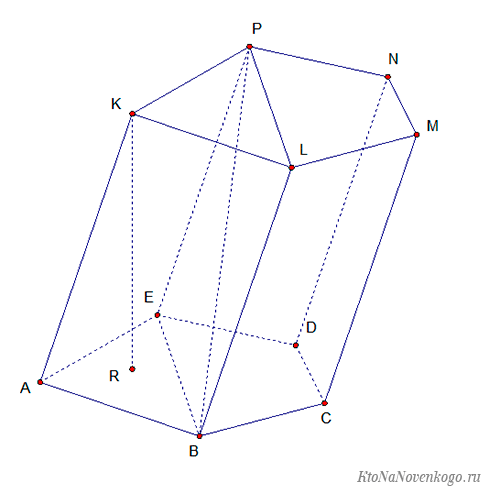
Элементы призмы
Рассмотрим для примера такую вот призму.
Она пятиугольная и состоит из следующих элементов:
Подобные элементы есть у каждой призмы, независимо от ее вида.
Разновидности призм
Все призмы можно поделить на три категории:
Вместо заключения
Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:
А еще «Призма» — это кодовое название советской радиостанции 5-АК. Есть такой хоккейный клуб в Латвии – «Призма-Рига». И наконец, в Финляндии существует сеть продуктовых магазинов «PRISMA».
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Спасибо! Хорошая статья.
Бедные дети, зачем им забивают голову всякими геометрическими призмами? Вообще, если провести опрос среди взрослых, понадобилось ли кому-нибудь это знание, уверен, мы не услышим ни одного положительного ответа.