Бутылка клейна для чего

Бутылка Клейна: свойства и применение

Бутылка Клейна – это двумерное многообразие, определенная не ориентируемая поверхность. Впервые она была описана немецким математиком Клейном в 1882 году. Если разрезать бутылку Клейна вдоль оси ее симметрии пополам на равные части, то в результате получится лента Мебиуса. Само название, скорее всего, происходит от неверного перевода с немецкого слова Flache – поверхность. По написанию это слово близко к слову Flasche – бутылка. В дальнейшем это название именно в таком варианте вернулось в немецкий язык.

Лента Мебиуса, бутылка Клейна и гептаэдр – все это представляет собой завершенные статические конструкции с вывернутыми наизнанку поверхностями. В 20-м веке топологи стали решать задачи динамического характера, и первой из них было выворачивание сферы. В отличие от вышеперечисленных фигур, поверхность сферы ориентирована. Ее внутреннюю сторону можно выкрасить в синий цвет, а внешнюю – в цвет красный. Если после такого окрашивания поверхностей поменять южный и северный полюса сферы местами, подвигая их вдоль соединяющей оси, то сфера окажется вывернутой наизнанку так, что ее внешняя поверхность станет синего цвета, а внутренняя – красного. По всей окружности экватора при этом образуется складка. Но и это еще не все: когда полюса пройдут вдоль оси большую часть пути и внешняя поверхность сферы изменит цвет с красного на синий, то по всей длине экватора создастся тороидальная поверхность, окрашенная с внешней стороны в красный цвет. Следовательно, вывернутая наполовину сфера показывает еще один занимательный эффект в топологии – переплетение внешнего и внутреннего пространства, так как с наружной стороны оказываются одновременно обе поверхности.

Как построить модель бутылки Клейна

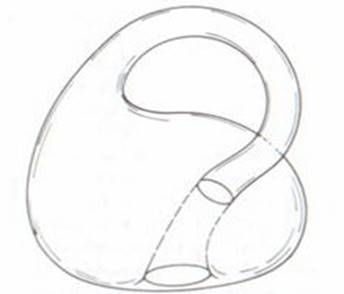
Для начала нужно взять бутылку с отверстиями в стенке и в донышке и вытянуть горлышко, изогнув его вниз и продев через отверстие в стенке. Если строить модель настоящей бутылки в четырехмерном пространстве, то в отверстии в стенке нет необходимости. Но без него не обойтись, если модель строится в трехмерном евклидовом пространстве (R3). Затем горлышко нужно присоединить к отверстию на дне. Бутылка Клейна, в отличие от обычного стакана, не имеет «края», где бы резко заканчивалась поверхность. Если сравнить ее с воздушным шаром, то путь изнутри наружу она проходит, не пересекая поверхность. Значит, в действительности объект не имеет ни внутренней, ни внешней поверхности.

Бутылка Клейна: применение и свойства

Это объект, как и лента Мебиуса, является двухмерным дифференцируемым не ориентируемым многообразием. Но, в отличие от ленты, бутылка Клейна является компактным многообразием без края. Если склеить по краям две ленты Мебиуса, то получится бутылка Клейна. Но это невозможно сделать в обычном пространстве (R3) без создания самопересечения. Бутылка Клейна может быть только погружена в трехмерное пространство, но при этом ее можно вложить в пространство четырехмерное. У данного объекта хроматическое число поверхностей равняется шести.

Источник

Бутылка Клейна

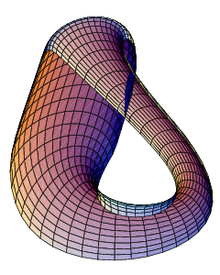
Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.

Чтобы построить модель бутылки Клейна, необходимо взять бутылку с двумя отверстиями: в донышке и в стенке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.

В отличие от обыкновенного стакана у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).

Более формально, бутылку Клейна можно получить склеиванием квадрата , идентифицируя точки (0,y)

(1,y) при и (x,0)

(1-x,1) при , как показано на диаграмме.

Содержание

Свойства

Рассечения

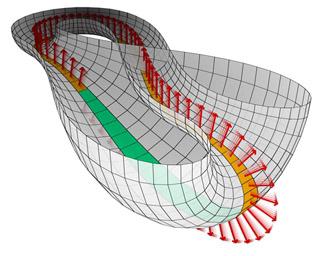
Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса, изображенная справа (необходимо помнить, что изображенного пересечения на самом деле нет).

Параметризация

Бутылка Клейна в виде восьмёрки имеет довольно простую параметризацию:

В этом виде самопересечение имеет форму геометрического круга в плоскости XY. Константа равна радиусу круга. Параметр задаёт угол на плоскости XY и обозначает положение около 8-образного сечения.

Бутылка Клейна в культуре

Некто Клейн, не любивший вина,
Раз придумал бутылку без дна.
Восклицал он: «К тому же
Что внутри — в ней снаружи!
Даже пробка совсем не нужна!»

См. также

Примечания

An anti-strong-drinker named Klein
Invented a bottle for wine.
«There’s no stopper», he cried,
«And it has no inside,
So the grapes have to stay on the vine!»

Ссылки

Полезное

Смотреть что такое «Бутылка Клейна» в других словарях:

Клейна поверхность — Бутылка Клейна, погружённая в трёхмерное пространство. Бутылка Клейна это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана … Википедия

Клейна поверхность — бутылка Клейна, замкнутая односторонняя поверхность (См. Односторонние поверхности), введённая в рассмотрение Ф. Клейном (1874). К. п. может быть получена из трубы (рис., а), открытой с обеих сторон, если, изогнув трубу, пропустить более… … Большая советская энциклопедия

Бутылка — Запрос «Бутылочка» перенаправляется сюда; см. также другие значения. Бутылка минеральной воды … Википедия

КЛЕЙНА ПОВЕРХНОСТЬ — бутылка Клепна, замкнутая односторонняя поверхность рода I (см. рис. 1, а, б). К. п. может быть получена из квадрата ABCD (см. рис. 2) отождествлением точек отрезков АВ и CD, лежащих на прямых, параллельных стороне AD, и точек отрезков ВС и AD,… … Математическая энциклопедия

Ваза Клейна — Бутылка Клейна, погружённая в трёхмерное пространство. Бутылка Клейна это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана … Википедия

Поверхность Клейна — Бутылка Клейна, погружённая в трёхмерное пространство. Бутылка Клейна это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана … Википедия

Клейн Ф. — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия

Клейн Феликс — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия

Феликс Клейн — Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия

Клейн, Феликс — Феликс Клейн Дата рождения: 25 апреля 1849(1849 04 25 … Википедия

Источник

Бутылка клейна для чего

Феликс Христиан Клейн

1.2 Основные достижения

Загадки бутылки Клейна

2.1 Строение бутылки Клейна

2.2 Конструирование бутылки Клейна

ВВЕДЕНИЕ

Тема работы и обоснование выбора темы

Предлагаемая вниманию читателя исследовательская работа посвящена необычной и загадочной бутылке Клейна.

Я обратила на нее внимание после того, как наткнулась на очень интересную статью в Интернете по поводу самых причудливо-простых изобретений. Свою будущую жизнь я хотела бы связать с математикой и физикой, поэтому данный прибор меня заинтересовал своим строением.

Актуальность темы моей работы определяется тем, что современные учащиеся считают математику и физику одними из самых скучных и бесполезных предметов, хотя на самом деле все, что нас окружает, в той или иной степени взаимосвязано с математикой и физикой, а это, кстати говоря, очень интересно.

На сегодняшний день существует множество работ по данной теме. Но новизна моей работы состоит в том, что таким образом я хочу показать учащимся математику и физику с занимательной интересной стороны, а не доказать какие-либо факты или закономерности.

Основной целью моей работы является рассмотрение бутылки Клейна с точки зрения математики.

Для достижения поставленной цели нам необходимо решить следующие задачи:

Охарактеризовать биографию Феликса Клейна;

Познакомится с основными достижениями Клейна;

Рассмотреть особенности строения бутылки Клейна;

Выявить способы конструирования бутылки Клейна.

Глава 1

Научная деятельность Феликса Клейна.

Биография Феликса Клейна

Феликс Христиан Клейн родился 25 апреля 1849 в Дюссельдорфе, в семье чиновника. Окончил гимназию в Дюссельдорфе, затем учился математике и физике в Боннском университете. Сначала планировал стать физиком. В это время Юлиус Плюккер заведовал отделением математики и экспериментальной физики в Бонне, и Клейн стал его ассистентом. Однако главным интересом Плюккера была геометрия. Под его руководством Клейн стал доктором в 1868.

В 1868 году Плюккер умер. Клейн совершает поездку по Германии, знакомится с Клебшем и другими крупными математиками.

В 1872 году Клейн становится профессором Эрлангенского университета.

В 1875 году женился на Анне Гегель, стал профессором в Высшей технической школе в Мюнхене. Позже работал в Лейпцигском университете. В1882 году после серьезной болезни, начал заниматься педагогической и общественной работой. С1888 года работал в Гёттингенском университете. Его лекции пользовались большим успехом, слушатели приезжали со всего мира. Умер Клейн на 76 году жизни.

Основные достижения Феликса Клейна

Клейн опубликовал более 20 работ по неевклидовой геометрии, теории групп Ли, теории многогранников и эллиптическим функциям. Одним из важнейших его достижений стало первое доказательство непротиворечивости геометрии Лобачевского. Он построил пример односторонней поверхности — «бутылку Клейна».

Именем Феликса Клейна названы:

Математический центр в Германии

Кратер на обратной стороне Луны

Приз Европейского математического общества и Технологического университета Кайзерслаутерна (присуждается молодым математикам Европы в ходе Европейского математического конгресса (каждые 4 года) за практически полезные работы в области прикладной математики)

Медаль Международной комиссии по математическому образованию.

Имя Клейна носят следующие математические объекты:

модель (интерпретация) Клейна

бутылка (поверхность) Клейна

На последнем изобретении мы бы хотели остановиться более подробно во второй главе.

Глава 2

Загадки бутылки Клейна.

2.1 Строение бутылки Клейна

Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г.немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиусаи проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Flache (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка).

Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз и, продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырёхмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве.

В отличие от обыкновенного стакана, у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара, можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).

2.2 Конструирование бутылки Клейна

Способ № 1.Получение бутылки Клейна из бумаги. Прежде всего, нужно взять бумажный квадрат, перегнуть его пополам и соединить клейкой лентой его стороны. На обращенной к вам половине квадрата сделайте прорезь, перпендикулярную склеенным сторонам. Расстояние между прорезью и верхним краем трубки должно быть равно примерно четверти стороны квадрата. Согнув модель пополам вдоль пунктирной прямой, протащите нижний край трубки сквозь прорезь и склейте друг с другом верхнее и нижнее основания трубки. Правда, там, где поверхность самопересекается, в нашей модели прорезь, но легко представить себе, что края этой прорези соединены так, чтобы поверхность во всех своих точках была непрерывна и не имела края.

Способ № 2. Получение бутылки Клейна из стандартной пластмассовой бутылки. Необходимо взять бутылку с отверстием в донышке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.

Способ № 3. Получение бутылки Клейна из одного цилиндра. Один из краёв цилиндра изгибается в обратную сторону, проходит сквозь цилиндр и склеивается с другим краем. Чтобы совершить это склеивание, необходимо исказить ширину цилиндра.

Способ № 4. Получение бутылки Клейна из ткани. Целесообразно взять кусок носка или колготок и проделать с ними то же, что и с цилиндром.

Способ № 5. Получение бутылки Клейна склеиванием двух листов Мёбиуса.Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространствесделать это, не создав самопересечения, невозможно.

Заключение

Все вышесказанное подводит нас к мысли, что математика таит в себе много нового, неизведанного и интересного.

Библиографический список

2.Е.С. Смирнова «Курс наглядной геометрии» 6 класс. «Просвещение»

3.Современный словарь иностранных слов. «Русский язык» 1993гг, стр.

«Аванта+»2001г., стр. 111-112.

6. Научно-исследовательская работа «Этот удивительный лист Мёбиуса»

Источник

Эксперименты с бутылкой Клейна

Дата публикации: 25.11.2014 2014-11-25

Статья просмотрена: 3659 раз

Библиографическое описание:

Первушкина, Е. А. Эксперименты с бутылкой Клейна / Е. А. Первушкина, Т. Д. Марушина. — Текст : непосредственный // Молодой ученый. — 2014. — № 21.1 (80.1). — С. 244-246. — URL: https://moluch.ru/archive/80/13829/ (дата обращения: 24.12.2021).

В данной статье представлены опыты с бутылкой Клейна. Поставлена проблема и решена экспериментально, прогнозирования экспериментов с разрезанием модели бутылки Клейна. Были выявлены ее свойства.

Ключевые слова: бутылка Клейна, лист Мебиуса, трехмерное пространство, топологическая поверхность.

Abstract. The article presents a series of experiments with the Klein bottle. Solves the problem of forecasting the result of the experiment with cutting the Klein bottle. We have also identified its properties.

Keywords: The Klein bottle, the Möbius strip, a three-dimensional space, topological surface.

Бутылка Клейна была описана немецким ученым Ф. Клейном в 1882 году.

С бутылкой Клейна знакомятся в высших учебных заведениях в курсе геометрии. Эта модель интересна тем, что ее свойства нельзя увидеть без проведения опытов, так как она не может существовать в нашем трехмерном пространстве. Модели, которые мы видим в магазинах, как сувенир имеют отдаленное представление о бутылки Клейна. Интересна возможность выявления свойств бутылки Клейна с помощью экспериментов.

Рис.1. Бутылка Клейна

Бутылка Клейна – это неориентируемая определённая поверхность [1, с. 352]. Она частично связана с лентой Мёбиуса (прямоугольная лента, полученная склеиванием противоположных сторон с поворотом на 180 градусов [3]) и проективной плоскостью.

Изготовление бутылки Клейна

А

Рис. 2. Изготовление бутылки Клейна

Сложите квадрат пополам и соедините его стороны, обозначенные пунктиром на рис.1 а). Сделайте прорезь на обращенной к вам половине квадрата, перпендикулярно склеенным сторонам рис.1 б). Между верхним краем и прорезью трубки должно быть расстояние равное четверти стороны квадрата. Перегнув модель пополам вдоль прямой А, протащите нижний край трубки сквозь прорезь, верхнее и нижнее основания трубки склейте друг с другом в соответствии со стрелками рис.1 в).

Видим, что склеить бутылку Клейна довольно сложно. Из прозрачного материала эта модель будет более наглядной. Далее проведем ряд экспериментов с бутылкой Клейна, описанных в таблице 1.

Вначале будут сделаны предположения, какой будет результат, затем проводится проверка высказанных нами предположений.

Разрезание бутылки Клейна

Высказанное предположение подтвердилось.

Высказанное предположение подтвердилось.

В результате мы получили два листа Мебиуса и цилиндр.

1. Склеили Бутылку Клейна и выполнили разрез посередине. Перед этим было высказано предположение, что результатом будет два листа Мебиуса. Данное высказывание подтвердилось.

2. Склеили бутылку Клейна, выполнили разрез по краю. Перед этим было высказано предположение, что получиться лист Мебиуса. Данное высказывание подтвердилось.

3. Склеили модель, выполнили два разреза по краям. Перед этим было высказано предположение, что результатом станет три листа Мебиуса. Высказанное предположение не подтвердилось. В результате были получены 2 листа Мебиуса и цилиндр.

Из проведенных нами опытов можно выделить следующие свойства бутылки Клейна:

2. Число Бетти – это число разрезов, которые можно провести так, чтобы поверхность не распалась на два отдельных куска [2, с. 507]. Так как бутылка Клейна не имеет краев (то есть поверхность замкнутая), то каждый разрез должен иметь форму какой-нибудь простой замкнутой кривой, поэтому число Бетти для нашей модели равно 2.

3. Хроматическое число (минимальное число цветов, в которые можно раскрасить модель так, чтобы концы любого ребра имели разные цвета) [5, с. 74]. Хроматическое число бутылки Клейна равно шести. Это означает, что на данной поверхности можно так расположить 6 областей разных цветов, чтобы 5 областей имели общие границы с шестой областью.

4. Бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием [6, с. 208]. Она, в отличие от листа Мёбиуса, является замкнутым многообразием, то есть компактным многообразием без края.

5. Она не может быть вложена в трёхмерное евклидово пространство Е₃ (только погружена), но вкладывается в Е₄.

6. Бутылка Клейна может быть получена склеиванием по краю двух лент Мёбиуса. Но в обычном трехмерном евклидовом пространстве Е₃ сделать это невозможно, не создав самопересечения.

Выполняя опыты, мы наблюдали затем, что происходит с бутылкой Клейна и делали правильные предположения. В то время как изначально наши предположения могли быть неверными. Значит, именно проведенные нами опыты делают свойства построенной поверхности более доступными для понимания.

В результате проведенных опытов, мы убедились, что действительно бутылка Клейна не может существовать в трехмерном пространстве, а лишь в четырехмерном. В наше время её можно встретить в магазинах, в рекламе, а также в шоу фокусников (иллюзионист, забравшись в бутылку, остается на половину погруженным в нее) [4, с. 28]. Изготовить бутылку Клейна из стекла достаточно сложно, поэтому она имеет высокую стоимость и применяется крайне редко.

1. Атанасян Л.С., Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. инс-ов. Ч-2. – М.: Просвещение, 1987. – 352 с.

2. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971. – 507 с.

3. Марушина Т.Д. Разрезание лент // Исследования в области естественных наук. 2014. № 7 [Электронный ресурс]. URL: http://science.snauka.ru/2014/07/7567 (дата обращения: 09.08.2014).

4. Пономарева Е.И., Первушкина Е.А. Развитие креативности школьников при обучение математике в 5-6 классах с использованием интерактивных геометрических средств // Перспективы науки. – 2011. – № 16. – С. 27-34.

6. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. – М.: МИРОС.КПЦ «Марта», 1992. – 208 с.

Источник