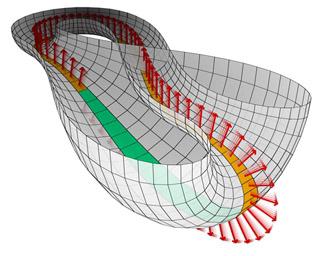
Бутылка клейна что это такое
Бутылка Клейна: свойства и применение
Бутылка Клейна – это двумерное многообразие, определенная не ориентируемая поверхность. Впервые она была описана немецким математиком Клейном в 1882 году. Если разрезать бутылку Клейна вдоль оси ее симметрии пополам на равные части, то в результате получится лента Мебиуса. Само название, скорее всего, происходит от неверного перевода с немецкого слова Flache – поверхность. По написанию это слово близко к слову Flasche – бутылка. В дальнейшем это название именно в таком варианте вернулось в немецкий язык.
Лента Мебиуса, бутылка Клейна и гептаэдр – все это представляет собой завершенные статические конструкции с вывернутыми наизнанку поверхностями. В 20-м веке топологи стали решать задачи динамического характера, и первой из них было выворачивание сферы. В отличие от вышеперечисленных фигур, поверхность сферы ориентирована. Ее внутреннюю сторону можно выкрасить в синий цвет, а внешнюю – в цвет красный. Если после такого окрашивания поверхностей поменять южный и северный полюса сферы местами, подвигая их вдоль соединяющей оси, то сфера окажется вывернутой наизнанку так, что ее внешняя поверхность станет синего цвета, а внутренняя – красного. По всей окружности экватора при этом образуется складка. Но и это еще не все: когда полюса пройдут вдоль оси большую часть пути и внешняя поверхность сферы изменит цвет с красного на синий, то по всей длине экватора создастся тороидальная поверхность, окрашенная с внешней стороны в красный цвет. Следовательно, вывернутая наполовину сфера показывает еще один занимательный эффект в топологии – переплетение внешнего и внутреннего пространства, так как с наружной стороны оказываются одновременно обе поверхности.
Как построить модель бутылки Клейна
Для начала нужно взять бутылку с отверстиями в стенке и в донышке и вытянуть горлышко, изогнув его вниз и продев через отверстие в стенке. Если строить модель настоящей бутылки в четырехмерном пространстве, то в отверстии в стенке нет необходимости. Но без него не обойтись, если модель строится в трехмерном евклидовом пространстве (R3). Затем горлышко нужно присоединить к отверстию на дне. Бутылка Клейна, в отличие от обычного стакана, не имеет «края», где бы резко заканчивалась поверхность. Если сравнить ее с воздушным шаром, то путь изнутри наружу она проходит, не пересекая поверхность. Значит, в действительности объект не имеет ни внутренней, ни внешней поверхности.
Бутылка Клейна: применение и свойства
Это объект, как и лента Мебиуса, является двухмерным дифференцируемым не ориентируемым многообразием. Но, в отличие от ленты, бутылка Клейна является компактным многообразием без края. Если склеить по краям две ленты Мебиуса, то получится бутылка Клейна. Но это невозможно сделать в обычном пространстве (R3) без создания самопересечения. Бутылка Клейна может быть только погружена в трехмерное пространство, но при этом ее можно вложить в пространство четырехмерное. У данного объекта хроматическое число поверхностей равняется шести.