Бросают игральный кубик найдите вероятность того что выпадет нечетное число очков
Бросили кость найти вероятность
Содержание:
Пример 1:
Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало 4 очка?
Решение:
элементарное событие: 4. Поэтому 
Элементарные события равновозможныс, поскольку подразумевается, что кубик честный. Поэтому
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Пример 2:
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых(слайд №5).
Решение:
Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6. Таких ячеек 5. Значит, событию А = <сумма выпавших очков равна 6>благоприятствует 5 элементарных исходов. Следовательно, 
Поэтому,
Возможно вам будут полезны данные страницы:
Пример 3:
Саша дважды бросает игральный кубик. В сумме у него выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 1 очко(слайд №6).
Решение:
Пример 4:
Тоня и Нина играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Тоня проиграла(слайд №7).
Решение:
Пример 5:
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых(слайд №8).
Решение:
Вероятность события
Лекции:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
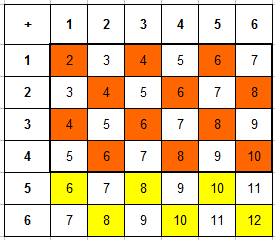
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
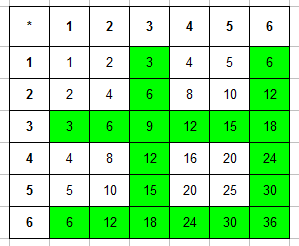
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
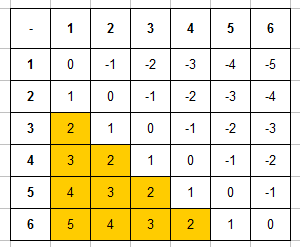
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
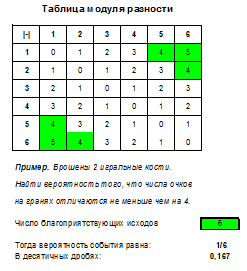
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):
Урок по теме «Решение задач по теории вероятностей»
Разделы: Математика
Тип урока: урок изучения нового материала.
Образовательные: создать условия для овладения учащимися системы знаний, умений и навыков с понятиями вероятности события.
Воспитательные: формировать у учащихся научное мировоззрение
Развивающие: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.
Методы организации учебно-познавательной деятельности:
Оборудование: мультимедийный проектор (презентация), карточки (самостоятельная работа)
Ход урока
I. Организационный момент.
Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина.
Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы.
Определить значимость изучаемого материала, как в данной теме, так и во все курсе.
II. Повторение
1. Что такое вероятность?
Вероятность – возможность исполнения, осуществимости чего-нибудь.
2. Какое определение дает основатель современной теории вероятностей А.Н. Колмогоров?
Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях.
3. Какое классическое определение вероятности дают авторы школьных учебников?
Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу n всех исходов испытания.
Вывод: в математике вероятность измеряется числом.
Сегодня мы с вами продолжим рассматривать математическую модель “игральная кость”.
Предметом исследования в теории вероятностей являются события, появляющиеся при определенных условиях, которые можно воспроизводить неограниченное количество раз. Каждое осуществление этих условий называют испытанием.
Испытание – бросание игральной кости.
Событие – выпадение шестерки или выпадение четного числа очков.
Выпадение каждой грани при многократном бросании кубика имеет одинаковую вероятность (игральная кость правильная).
III. Устное решение задач.
1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало 4 очка?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Граней всего шесть. Перечислим все события: 1, 2, 3, 4, 5, 6. Значит п = 6. Событию А = <выпало 4 очка>благоприятствует одно событие: 4. Поэтому т = 1. События равновозможные, поскольку подразумевается, что кубик честный. Поэтому Р(А) = т/п = 1/6 = 0,17.
2. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не более 4 очков?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = <выпало не более 4 очков>благоприятствует 4 события: 1, 2, 3, 4. Поэтому т = 4. Поэтому Р(А) = т/п = 4/6 = 0,67.
3. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало менее 4 очков?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = <выпало менее 4 очков>благоприятствует 3 события: 1, 2, 3. Поэтому т = 3. Р(А) = т/п = 3/6 = 0,5.
4. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало нечетное число очков?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = <выпало нечетное число очков>благоприятствует 3 события: 1,3,5. Поэтому т = 3. Р(А) = т/п = 3/6 = 0,5.
IV. Изучение нового
Сегодня рассмотрим задачи, когда в случайном эксперименте используются две игральные кости или выполняются два, три броска.
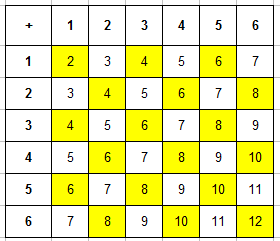
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых.
Решение. Исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество исходов удобно представить таблицей.
Строки соответствуют количеству очков на первом кубике, столбцы – на втором кубике. Всего элементарных событий п = 36.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
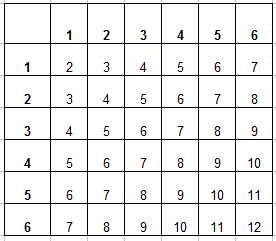
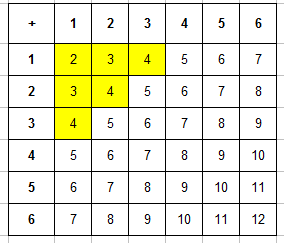
Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6.
Таких ячеек 5. Значит, событию А = <сумма выпавших очков равна 6>благоприятствует 5 исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14.
2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 3 очка. Результат округлите до сотых.
Решение. Исход в этом опыте – упорядоченная пара чисел. Всего событий п = 36.
Событию А = <сумма равна 3>благоприятствуют 2 исходов. Следовательно, т = 2.
Поэтому, Р(А) = 2/36 = 0,06.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет более 10 очков. Результат округлите до сотых.
Решение. Исход в этом опыте – упорядоченная пара чисел. Всего событий п = 36.
Событию А = <в сумме выпадет более 10 очков>благоприятствуют 3 исхода.
Следовательно, т = 3. Поэтому, Р (А) = 3/36 = 0,08.
4. Люба дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.
Решение Исход в этом опыте – упорядоченная пара чисел. Первое число выпадет при первом броске, второе – при втором. Множество исходов удобно представить таблицей.
Строки соответствуют результату первого броска, столбцы – результату второго броска.
Всего событий, при которых сумма очков 9 будет п = 4. Событию А = <при одном из бросков выпало 5 очков>благоприятствует 2 исхода. Следовательно, т = 2.
Поэтому, Р(А) = 2/4 = 0,5.
5. Света дважды бросает игральный кубик. В сумме у неё выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 1 очко.
Равновозможных исходов – 5.
Благоприятствующих исходов – 2.
Вероятность события р = 2/5 = 0,4.
6. Оля дважды бросает игральный кубик. В сумме у нее выпало 5 очков. Найдите вероятность того, что при первом броске выпало 3 очка.
Равновозможных исходов – 4.
Благоприятствующих исходов – 1.
Вероятность события р = 1/4 = 0,25.
7. Наташа и Витя играют в кости. Они бросают игральную кость по одному разу.
Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 8 очков. Найдите вероятность того, что Наташа выиграла.
Равновозможных исходов – 5.
Благоприятствующих исходов – 2.
Вероятность события р = 2/5 = 0,4.
8. Таня и Наташа играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Таня проиграла.
Равновозможных исходов – 5.
Благоприятствующих исходов – 2.
Вероятность события р = 2/5 = 0,4.
9. Коля и Лена играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. Первым бросил Коля, у него выпало 3 очка. Найдите вероятность того, что Лена не выиграет.
У Коли выпало 3 очка.
У Лены равновозможных исходов – 6.
Благоприятствующих проигрышу исходов – 3 (при1 и при 2 и при 3).
Вероятность события р = 3/6 = 0,5.
10. Маша трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут чётные числа.
У Маши равновозможных исходов – 6 · 6 · 6 = 216.
Благоприятствующих проигрышу исходов – 3 · 3 · 3 = 27.
Вероятность события р = 27/216 = 1/8 = 0,125.
11. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Первая
Равновозможных исходов – 6 · 6 · 6 = 216.
Благоприятствующих исходов – 6.
Вероятность события р = 6/216 = 1/36 = 0,277… = 0,28. Следовательно, т = 3. Поэтому, Р (А) = 3/36 = 0,08.
V. Самостоятельная работа.VI. Домашняя работа
VII. Итог урока
Что нужно знать для нахождения вероятности случайного события?
Для вычисления классической вероятности нужно знать все возможные исходы события и благоприятные исходы.
Классическое определение вероятности применимо только к событиям с равновозможными исходами, что ограничивает область его применения.
Для чего в школе изучаем теорию вероятности?
Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей.
Бросают игральный кубик найдите вероятность того что выпадет нечетное число очков
Брошена игральная кость. Какова вероятность того, что выпадет чётное число очков?
1, 3, 5 — нечетные числа; 2, 4, 6 — четные. Число возможных исходов при бросании игральной кости 6. Число благоприятных исходов 3 (выпадение двойки, четвёрки или шестёрки). Таким образом, вероятность выпадения четного числа очков равна три к шести или 0,5.
Брошена игральная кость. Какова вероятность того, что выпадет число меньше 4?
Другими словами, какова вероятность того, что выпадет либо единица, либо двойка, либо тройка? Число возможных исходов 6. Число благоприятных исходов 3 (выпадение единицы, двойки или тройки). Таким образом, вероятность выпадения числа меньшего четырёх будет 3 к 6 или 3/6=0,5.
В ящике 6 белых и 4 чёрных шара. Какова вероятность того, что первый наудачу выбранный шар окажется белым?
Всего шаров 10, значит число возможных исходов 10. Число благоприятных исходов 6 (в ящике 6 белых шаров). Вероятность того, что первый выбранный шар окажется белым 6 к 10, то есть 6/10=0,6
Набирая номер телефона, абонент забыл последнюю цифру. Какова вероятность того, что он правильно дозвонится, набрав последнюю цифру наугад?
Абоненту нужно выбрать одну из десяти цифр, то есть число возможных исходов 10. Число благоприятных исходов 1 (верной может быть только одна цифра). Вероятность того, что он правильно дозвонится равна 1 к 10 или 0,1.
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число 56?
Число возможных исходов 100 (сто чисел). Верно названное число одно это 56, значит благоприятный исход один. Вероятность того, что он назовёт число 56 будет один к ста или 0,01.
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число кратное пяти?
Число возможных исходов 100 (сто чисел). Чисел кратных пяти двадцать (перечислим):5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100. То есть число благоприятных исходов 20. Вероятность того, что ученик назовёт число кратное пяти равна 20 к 100 или 20/100=0,2.
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число, принадлежащее промежутку от 5 до 20 включительно?
Число возможных исходов 100. Число благоприятных исходов 16: это числа от 5 до 20 (5,6…..19,20), причём 5 и 20 входят в промежуток (в условии сказано «от 5 до 20 включительно»). Искомая вероятность равна 16/100.
В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. На вызов выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Возможное число исходов 10. Число благоприятных исходов 1 (жёлтая машина одна). Искомая вероятность равна 1 к 10 или 0,1.
Валя выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.
При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что первый раз выпало меньше трёх очков.
Монету бросают трижды. Найдите вероятность того, первые два броска окончатся одинаково.
Найдём число возможных исходов, переберём все варианты бросков. В подобных задачах составляйте таблицу, так считать на много удобней.
- Бросают игральную кость найти вероятность того что выпадет четное число очков
- Бросают кубик равновозможными событию выпадения шестерки являются события что