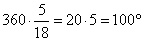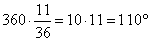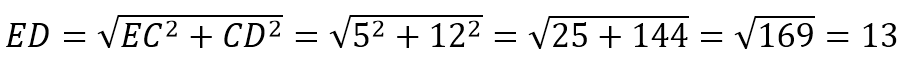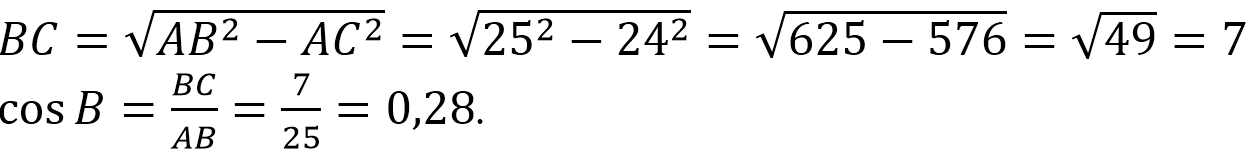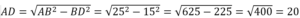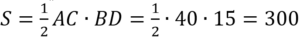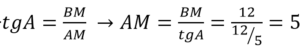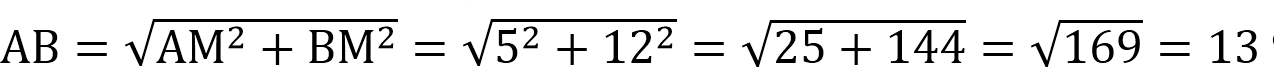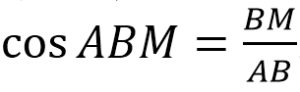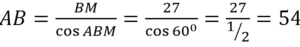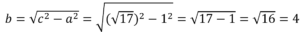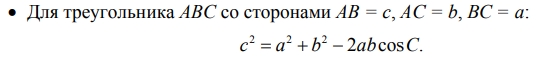В треугольнике известно что

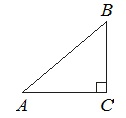
В треугольнике известно что

В треугольнике ABC стороны AC = 37,5, BC = 20, угол C равен 90°. Найдите радиус вписанной окружности.

В треугольнике ABC известно, что угол C равен Найдите радиус вписанной окружности.

В треугольнике ABC известно, что угол C равен Найдите радиус вписанной окружности.

Именно так и вычислили

В треугольнике ABC стороны AC = 12, BC = 5, угол C равен 90°. Найдите радиус вписанной окружности.

В треугольнике ABC стороны AC = 24, BC = 10, угол C равен 90°. Найдите радиус вписанной окружности.

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

Источник

Задание №15 ЕГЭ по математике базового уровня

Планиметрия

В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.

Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня

Вариант 15МБ1

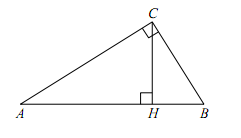
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.

Алгоритм выполнения:

Решение:

Вспомним определение косинуса угла.

Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.

Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.

Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.

Прилежащий к углу А катет – АН.

Получим cos A = АН/АС.

Выразим неизвестную величину.

АН = АС · cos A = 4 · 0,8 = 3,2

Вариант 15МБ2

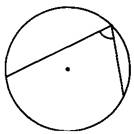
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 5/18 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ3

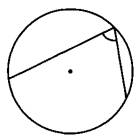
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 11/36 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ4

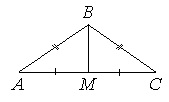
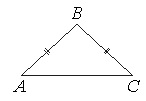
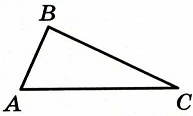
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.

Алгоритм выполнения

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Решение:

Если АВ=ВС, то ∆АВС – равнобедренный.

.

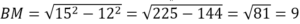
Вариант 15МБ5

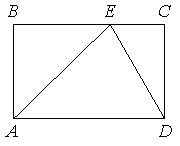
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.

Алгоритм выполнения

Решение:

Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.

Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.

Вариант 15МБ6

Алгоритм выполнения

Решение:

Вариант 15МБ7

В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.

Алгоритм выполнения

Решение

В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.

Из ∆ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 →

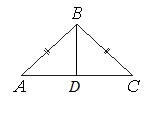
Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.

Вариант 15МБ8

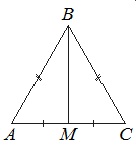
В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.

Алгоритм выполнения

Решение:

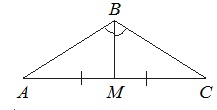
Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.

Из ∆АВМ по теореме Пифагора АВ 2 =АМ 2 +ВМ 2 →

Вариант 15МБ9

Алгоритм выполнения

Решение:

По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет

Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.

В прямоугольного ∆АМВ:

Вариант 15МБ10

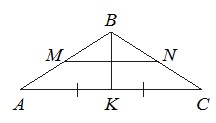
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.

Алгоритм выполнения

Решение:

Поскольку ВК медиана, то АС=2АК=2·24=48.

Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).

Вариант 15МБ11

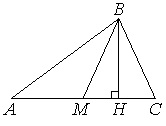
В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.

Алгоритм выполнения

Решение:

Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.

По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.

Вариант 15МБ12

Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.

Алгоритм выполнения

Решение:

Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.

Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.

Вариант 15МБ13

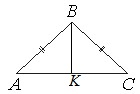
В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.

Алгоритм выполнения

Решение:

Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.

Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.

Источник

Решение №2593 В треугольнике ABC известно, что АВ = 6, ВС = 8, АС = 4.

В треугольнике ABC известно, что АВ = 6, ВС = 8, АС = 4. Найдите cos∠ABC.

Источник: ОГЭ Ященко 2022 (36 вар)

Из справочного материала ОГЭ используем теорему косинусов:

У нас АС = с (противолежащая искомому углу сторона), АВ = а, ВС = b, cos ∠B:

AC 2 = AB 2 + BC 2 – 2·AB·BC·cos∠АВС
4 2 = 6 2 + 8 2 – 2·6·8·cos∠АВС
16 = 36 + 64 – 96·cos∠АВС
96·cos∠АВС = 36 + 64 – 16
96·cos∠АВС = 84
cos∠АВС = 84/96 = 7/8 = 0,875

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Источник

Решение №1652 В треугольнике ABC известно, что AB=5, BC=10, AC=11.

В треугольнике ABC известно, что AB = 5, BC = 10, AC = 11. Найдите cos∠ABC.

Источник: ОГЭ Ященко 2022 (36 вар)

Из справочного материала ОГЭ используем теорему косинусов:

У нас АС = с (противолежащая искомому углу сторона), АВ = а, ВС = b, cos ∠B:

AC 2 = AB 2 + BC 2 – 2·AB·BC·cos∠АВС
11 2 = 5 2 + 10 2 – 2·5·10·cos∠АВС
121 = 125 – 100·cos∠АВС
100·cos∠АВС = 125 – 121
100·cos∠АВС = 4
cos∠АВС = 4/100 = 0,04

Ответ: 0,04.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.2 / 5. Количество оценок: 9

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Источник