В произвольной трапеции aknd известно что ad параллельно kn точка о

07.09.202310.09.2023 admin 0 Comments

В произвольной трапеции aknd известно что ad параллельно kn точка о

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

`d_1^2+d_2^2=c_1^2+c_2^2+2ab`.

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

Источник

Задача 16 геометрия на ЕГЭ-2021 по математике

Все они имеют нечто общее: во-первых, это стандартный уровень сложности, то есть вполне решаемые задачи. Пункт (а) в них вообще простой.

Во-вторых, в каждой из них применяются свойства четырехугольников, вписанных в окружности.

В первой задаче такая окружность находится почти сразу, причем она – вспомогательная, и ее можно даже не изображать на чертеже. Главное – найти равные вписанные углы, опирающиеся на равные дуги или на одну дугу.

Также здесь использована формула синуса тройного угла. Если вы ее забыли – не беда. Ведь а формулу синуса суммы вы знаете.

1. Дана равнобедренная трапеция ABCD, в которой меньшее основание ВС равно боковой стороне. Точка Е такова, что ВЕ перпендикулярно AD и СЕ перпендикулярно BD.
а) Доказать, что угол АЕВ равен углу BDA.
б) Найти площадь трапеции ABCD, если АВ = 32, косинус угла АDВ равен

– равнобедренный, CM – высота, проведенная к основанию, значит, M – середина BD.

Докажем, что точки A, B, C, D, E лежат на одной окружности.

ABCD – равнобедренная трапеция, ее можно вписать в окружность.

В – медиана и высота, значит, равнобедренный, BE = ED.

Тогда по трем сторонам, четырехугольник BCDE можно вписать в окружность, т.к.

Так как вокруг можно описать только одну окружность и вокруг четырехугольников ABCD и BCDE тоже можно описать окружность, точки A, B, C, D, E лежат на одной окружности, так как опираются на одну и ту же дугу AB (точки E и D лежат по одну сторону от прямой AD).

б) Так как AB = BC = CD, то дуги AB, BC и CD также равны.

Четырехугольник ABDE вписан в окружность, тогда

По формуле синуса тройного угла,

тогда по теореме синусов

Проведем в трапеции ABCD высоту CK, тогда

BH и CK – высоты трапеции, а так как трапеция равнобедренная, то

Во второй задаче мы увидим ту же идею: вспомогательную окружность. Это один из методов, помогающих решать задачи ЕГЭ по геометрии. Есть здесь и другой мощный прием – использование двух пар подобных треугольников. И еще свойство высоты прямоугольного треугольника, проведенной к гипотенузе. Если вы в восьмом и девятом классе учили геометрию – вы должны владеть этими приемами.

2. Дан прямоугольный треугольник АВС с прямым углом С. Из вершины С на гипотенузу опущена высота СН, на АС и ВС соответственно отмечены точки М и N так, что угол MHN – прямой.
а) Докажите, что треугольники МNH и АВС подобны.
б) Найдите СN, если АС = 5, СМ = 2, ВС = 3.

а) Рассмотрим четырехугольник CMHN.

по условию, значит, CMHN можно вписать в окружность; вписанные, опираются на дугу HN.

Запишем соотношение сходственных сторон.

По условию, AM = 3, найдем CH — высоту

по теореме Пифагора,

AH — проекция катета AC на гипотенузу, по свойствам прямоугольного треугольника, отсюда

В следующей задаче мы снова видим окружность и вписанную в нее трапецию. И наверное, вы уже заметили: пункт (а) задач по геометрии на ЕГЭ часто оказывается подсказкой для решения пункта (б). То, что мы доказали в (а), мы используем в пункте (б).

3. Даны 5 точек на окружности: A, B, C, D, E, причем АЕ = ED = CD, ВЕ перпендикулярен АС.
Точка Т – точка пересечения АС и BD.
а) Докажите, что отрезок ЕС делит отрезок ТD пополам.
б) Найдите площадь треугольника АВТ, если BD = 10, АЕ =

Докажем, что M — середина TD.

Если AE = ED = DC, то дуги AE, ED, DC, также равны;

— накрест лежащие, при пересечении AC и DE секущей CE, значит, AEDC — равнобедренная трапеция. значит, BD — диаметр окружности.

(опирается на диаметр), по катету и гипотенузе, тогда DM — биссектриса равнобедренного т.к. — равнобедренный, то DM — медиана M — середина CE, кроме того, DM — высота

В — медиана и высота, значит, — равнобедренный, а так как — накрест лежащие, при параллельных прямых AC и DE и секущей CE, то по боковой стороне и углу при основании, тогда

Мы нашли, что AE = ED = CD = CT = ET.

BD = 10 — диаметр окружности.

— равнобедренный, AE = ET, — высота и медиана

Тогда BN — медиана и высота — равнобедренный, AB = BT.

Обозначим тогда — опираются на дугу AE,

Из по теореме синусов:

И еще одна трапеция, вписанная в окружность. Теперь вы точно выучите ее свойства наизусть! Также здесь применяется теорема о пересекающихся хордах. Все эти полезные теоремы, свойства и признаки можно найти в нашей универсальной шпаргалке – Справочнике Анны Малковой для подготовки к ЕГЭ по математике. Скачать Справочник бесплатно можно здесь.

4. Трапеция с большим основанием AD и высотой ВН вписана в окружность. Прямая BH пересекает окружность в точке К.

б) Найдите AD, если: радиус окружности равен шести, СК пересекается с AD в точке N и площадь четырехугольника BHNC в 24 раза больше, чем плошать треугольника KHN.

а) Трапеция ABCD вписана в окружность, следовательно, AB = CD (трапеция равнобокая)

Тогда — вписанные, опираются одну и ту же на дугу AK;

следовательно, CK — диаметр окружности, так как вписанный угол, опирающийся на диаметр, прямой; — опирается на диаметр CK, значит,

(опираются на дугу BC), тогда

Обозначим так как HE = BC,

Из подобия треугольников KNH и KCB следует, что тогда

По теореме о пересекающихся хордах,

Представив левую часть уравнения как разность квадратов, получим:

По смыслу задачи тогда и значит

Задача по геометрии на ЕГЭ по математике оценивается в 3 балла. Как видите, в 2021 году эти 3 балла за геометрию можно было получить без особенных трудностей. На нашем Онлайн-курсе подготовки к ЕГЭ мы решаем и такие задачи по геометрии, и более сложные. Если ты сейчас в 10-м или в 11-м классе – попробуй бесплатно Демо-доступ к Онлайн-курсу.

5. (Резервный день) Окружность с центром О, построенная на катете АС прямоугольного треугольника АВС, как на диаметре, пересекает гипотенузу АВ в точках А и D. Касательная, проведенная к этой окружности в точке D, пересекает катет ВС в точке М.

А) Докажите, что ВМ = СМ
Б) Прямая DM пересекает прямую АС в точке Р, прямая ОМ пересекает прямую ВР в точке К.

Найдите ВК : КР, если

а) Так как – радиус окружности, – равнобедренный, так как (касательная перпендикулярна радиусу, проведенному в точку касания), тогда

– угол между касательной и хордой,

Тогда т.е. – высота – прямоугольный, – равнобедренный, отсюда

Найдем BK : KP, если тогда

Источник

Произвольная трапеция

Свойства трапеции:

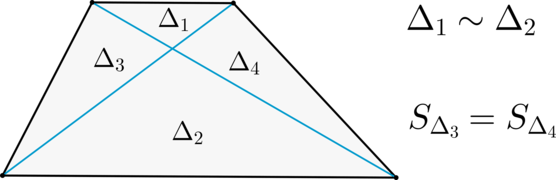
$\blacktriangleright$ Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

$\blacktriangleright$ Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.

Площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

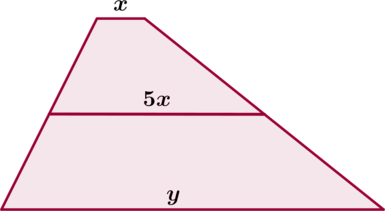
Одно из оснований трапеции в $5$ раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?

В трапеции $ABCD$ средняя линия составляет $\dfrac<4><5>$ одного из оснований. Найдите отношение длины другого основания к длине средней линии.

Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.

Как подготовиться к экзамену?

Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.

Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».

«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Источник