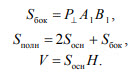В каком случае говорят что плоскости пересекаются

Предмет стереометрии. Аксиомы стереометрии

Стереометрия – это раздел геометрии, в котором изучают свойства фигур в пространстве. Слово “стереометрия” происходит от греческих слов “стереос” – объёмный, пространственный и “метрео” – измерять.

Самыми простыми и основными фигурами в пространстве являются точки, прямые и плоскости. Наряду с этими фигурами рассматривают геометрические тела и их поверхности. Представление о геометрических телах дают окружающие нас предметы. Поверхности тел составленные из многоугольников называются многогранниками. Одним из простейших многогранников является куб (кубик рубик имеет форму куба). Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром. Такую же форму имеет футбольный мяч. Консервная банка имеет форму геометрического тела, называемого цилиндром.

В отличии от реальных предметов геометрические тела, ка и всякие геометрические фигуры, являются воображаемыми объектами. Мы представляем геометрическое тело как часть пространства, определённую от остальной части пространства поверхностью – границей этого тела. Граница шара есть сфера, а граница цилиндра состоит из двух кругов – оснований цилиндра и боковой поверхности.

Изучая свойства геометрических фигур – воображаемых объектов, мы получаем представление о геометрических свойствах реальных предметов (их формы, взаимное расположение и так далее) и можем применять эти свойства на практике.

При изучении планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается ещё одна основная фигура – плоскость. Представление о плоскости даёт гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе как простирающийся неограниченно во все стороны.

Плоскости обозначатся греческими буквами α, β, γ и так далее. На рисунках плоскости обозначаются в виде параллелограмма или в виде произвольной области

Понятно, что в каждой плоскости лежат какие-то точки пространства, но не все точки пространства лежат в одной и той же плоскости.

Источник

Пересекающиеся плоскости

Плоскость — это одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Линия пересечения двух плоскостей — это прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Содержание:

Понятие пересекающихся плоскостей

Определение. Плоскости, которые имеют хотя бы одну общую точку, называют пересекающимися.

Аксиома 5. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой . Плоскости и в этом случае являются пересекающимися по прямой (рис. 2.379).

Пример:

Дана плоскость . Доказать, что существует другая плоскость (3, пересекающая .

Решение:

Из условия задачи имеем:

1. Плоскость (дано) (рис. 2.380).

2. Нужно доказать, что существует другая плоскость , пересекающая .

Мы знаем, что на основании аксиомы 3 (аксиомы плоскости) три точки определяют единственную плоскость.

3. Возьмем точки А и В, принадлежащие плоскости , и точку С, не лежащую на прямой АВ и не принадлежащую (построение) (рис. 2.381).

4. Точки А, В и С не лежат на одной прямой. Через них можно провести плоскость , и притом только одну (3, аксиома 3).

5. Плоскости и имеют общую точку (1, 3, 4).

6. Плоскости и пересекаются по прямой АВ (5, аксиома 5) (рис. 2.382).

7. Мы доказали, что существует плоскость Р, пересекающая . (6)

Замечание. Если допустить, что точка С лежит на прямой АВ, то она будет лежать и в плоскости , что противоречит выбору точки С.

Двугранные углы

При пересечении плоскостей образуются двугранные углы.

Определение. Фигуру, образованную двумя полуплоскостями, исходящими из одной прямой, называют двугранным углом. Прямую называют ребром, а полуплоскости — сторонами или гранями двугранного угла.

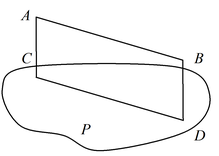
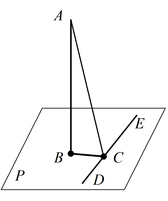
На рисунке 2.383 изображен двугранный угол с ребром АВ.

Этот угол можно обозначать двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежит несколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, одна крайняя — у одной грани, другая — у другой (рис. 2.384).

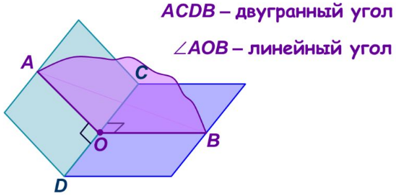
Определение. Если через произвольную точку ребра двугранного угла провести плоскость, перпендикулярную ребру, то в пересечении этой плоскости с двугранным углом образуется угол, который называют линейным углом двугранного угла.

На рисунке 2.385 изображен линейный угол АОВ двугранного угла АОСВ. Вершиной линейного угла служит точка О, лежащая на ребре ос двугранного угла, а сторонами — лучи граней, исходящие из точки о и перпендикулярные ребру двугранного угла.

Двугранный угол имеет бесконечное множество линейных углов (рис. 2.386).

Определение. Градусной мерой двугранного угла называют градусную меру любого из его линейных углов.

Определение. Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).

Можно доказать следующее утверждение.

Теорема 1. Все линейные углы двугранного угла равны друг другу.

Для двугранных углов так же, как и для плоских, вводится понятие его градусной меры — величины.

Определение. Два двугранных угла называют равными, если они имеют одну и ту же градусную меру.

Если градусная мера одного из двугранных углов больше градусной меры другого, то говорят, что первый двугранный угол больше второго, а второй меньше первого. На рисунке 2.387 изображены три двугранных угла с общим ребром АВ. Двугранные углы CABD и DABE равны, так как их градусные меры равны 30°. Двугранный угол САВЕ больше двугранного угла CABD.

Подобно плоским углам, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

Все сказанное можно сформулировать в виде теорем.

Теорема 2. 1. Равным двугранным углам соответствуют равные линейные углы.

2. Большему двугранному углу соответствует больший линейный угол.

Верна и обратная теорема.

Теорема 3. 1. Равным линейным углам соответствуют равные двугранные углы.

2. Большему линейному углу соответствует больший двугранный угол.

Из теорем 2 и 3 легко получить три следствия.

Следствие 1. Прямому двугранному углу соответствует прямой линейный угол, и обратно.

Следствие 2. Все прямые двугранные углы равны, потому что у них равны линейные углы.

Следствие 3. Вертикальные двугранные углы равны.

Пример:

Из условия теоремы имеем:

1. PABQ и — два данных двугранных угла (рис. 2.388).

2. Вложим угол в угол АВ так, чтобы ребро совпало с ребром АВ, а грань — с гранью Р (построение) (рис. 2.389).

3. Если эти двугранные углы равны, то грань совпадает с Q; если же двугранные углы не равны, то грань займет некоторое положение, не совпадающее с Q, например положение (1, 2).

4. Возьмем на общем ребре какую-нибудь точку В и проведем через нее плоскость , перпендикулярную ребру АВ (построение) (рис. 2.390).

5. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы.

Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол cbd; если же двугранные углы не совпадут (если, например, грань займет положение то у большего двугранного угла окажется больший линейный угол (именно ) (3, 4).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Основные понятия, аксиомы и теоремы стереометрии

Основные понятия стереометрии

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.

Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.

Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.

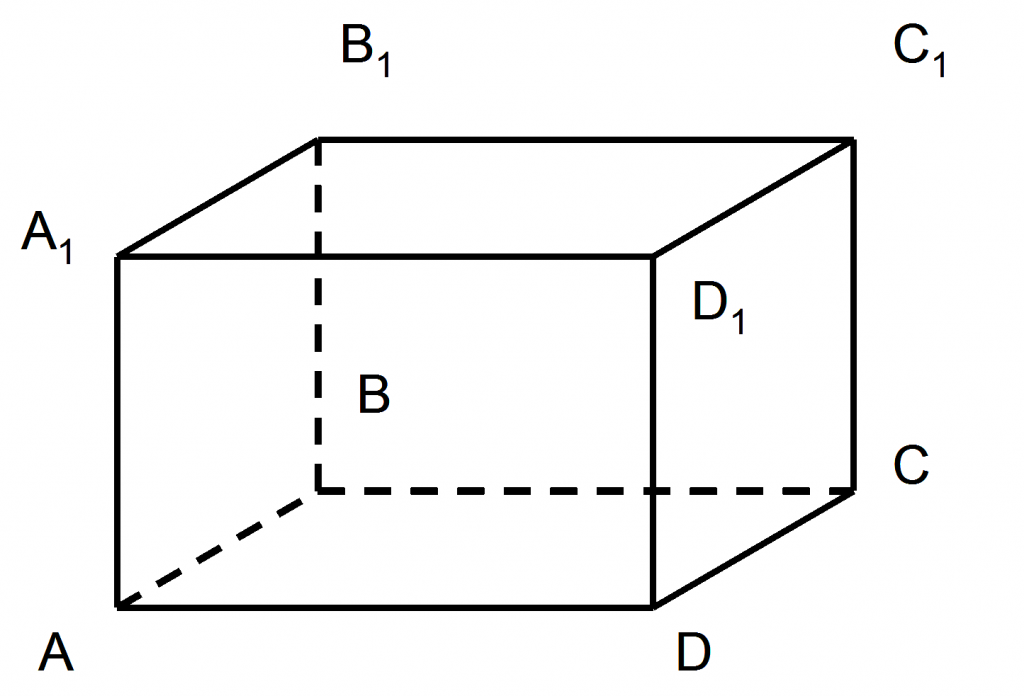
Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.

Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.

Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.

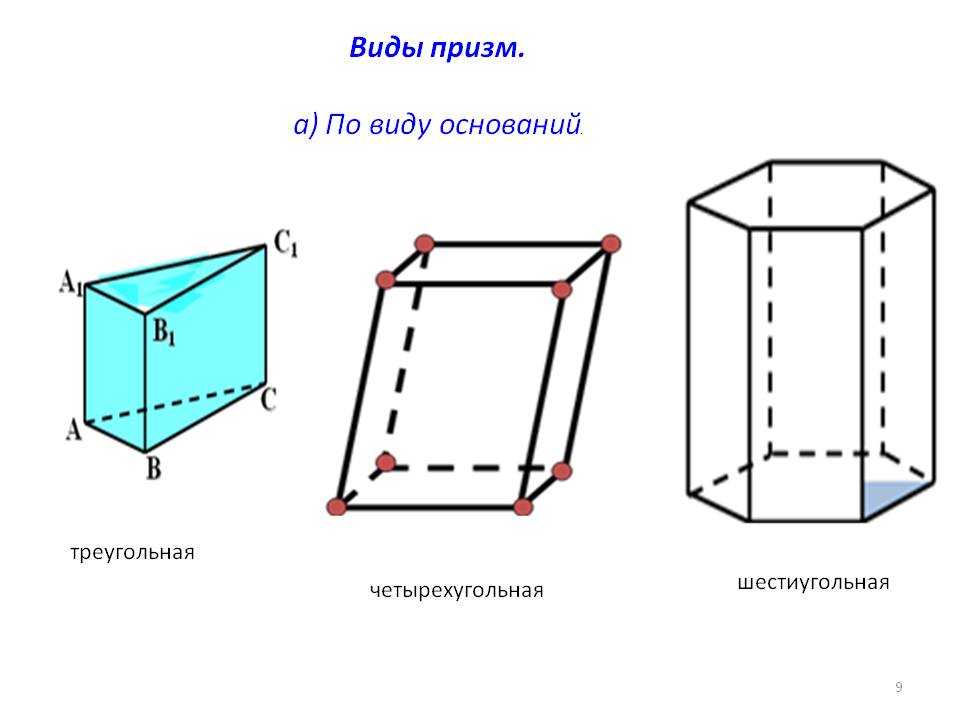
Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы.

Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.

Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).

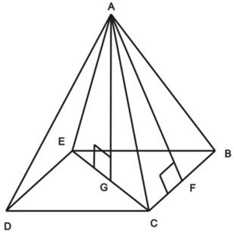
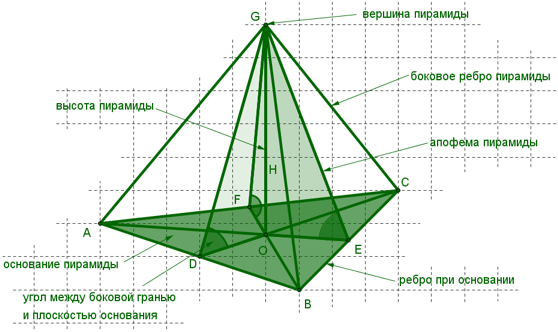
Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.

Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).

Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.

Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).

Аксиомы стереометрии

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.

Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Следствия из аксиом

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна.

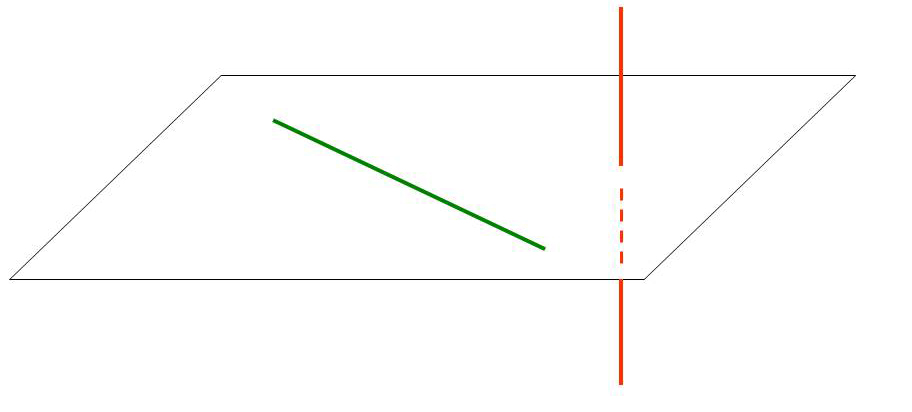
Следствие 4. Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Основные теоремы стереометрии

Теоремы о параллельности прямых и плоскостей

Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут: a // β

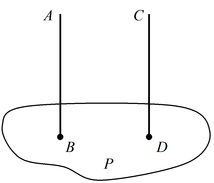
Теорема 1: Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.

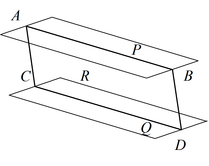
Теорема 2: Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.

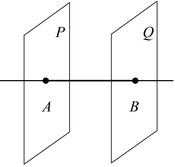
Теорема 3: Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.

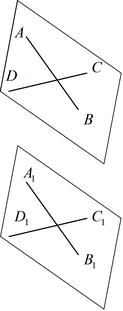
Теорема 4: Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A₁ B₁ и C₁ D₁ другой плоскости, то эти плоскости параллельны.

Теоремы о перпендикулярности прямых и плоскостей

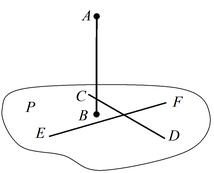
Теорема 1: Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.

Теорема 2: Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P (Достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: AC, BC, DE).

Теорема 3: Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.

Теорема 4: Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.

Теоремы о перпендикулярности плоскостей

Двугранный угол называется прямым, если его линейный угол прямой. Прямой двугранный угол равен смежному с ним двугранному углу.

Определение: Две плоскости называются взаимно перпендикулярными, если они образуют прямые двугранные углы.

Теорема 1:Перпендикулярность прямых в пространстве. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они то же перпендикулярны.

Теорема 2: Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.

Следствие 1: Если из точки одной из двух взаимно перпендикулярных плоскостей проведен перпендикуляр к другой плоскости, то он принадлежит первой плоскости.

Следствие 2: Если две плоскости, перпендикулярные к третьей плоскости, пересекаются, то их линия пересечения есть перпендикуляр к этой плоскости.

Теорема о скрещивающихся прямых

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

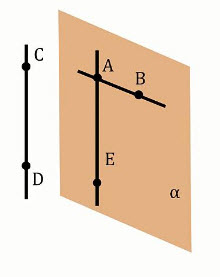
Теорема 1: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Теорема 2: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Пусть нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.

Проведем через точку А прямую АЕ, параллельную прямой DC (Рис. 6.). По теореме о параллельных прямых, такая прямая существует и единственная. Тогда через две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α. Так как прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости α, значит, что прямая DC параллельна плоскости α, по признаку параллельности прямой и плоскости. Существование доказано.

Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямая DC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α – единственная. Теорема доказана.

Теорема о трех перпендикулярах

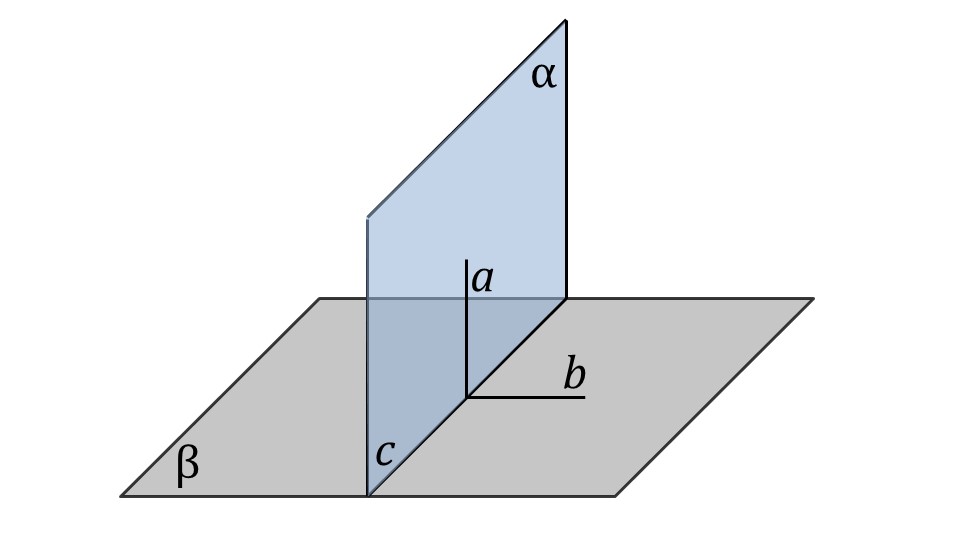
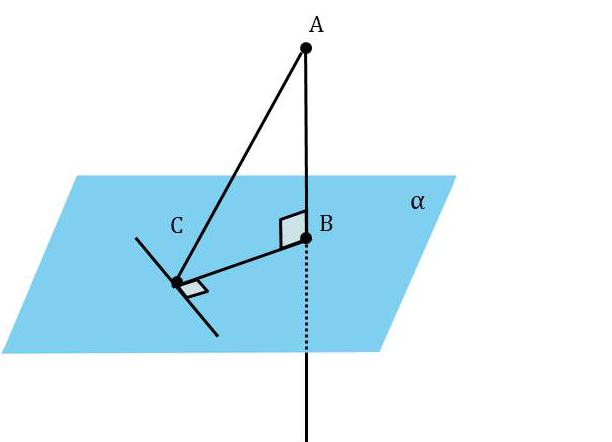
Теорема 2: (о трех перпендикулярах). Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость.

Доказательство.

Пусть AB — перпендикуляр к плоскости a, AC — наклонная и c — прямая в плоскости

Взаимное расположение прямых в пространстве

Основные фигуры в стереометрии

Симметрия фигур

Двугранный угол

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.

Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).

Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.

Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.

Две плоскости называются перпендикулярными, если угол между ними равен 90°.

Теорема 1: (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Теорема 2: Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.

Призма

Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.

Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.

Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.

Боковая поверхность – объединение боковых граней.

Полная поверхность – объединение оснований и боковой поверхности.

Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.

Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.

Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.

Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру. Площадь поверхности и объём призмы.

Параллелепипед

Параллелепипедом называется призма, основанием которой служит параллелограмм.

Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны – ребрами, а вершины параллелограммов – вершинами параллелепипеда.

У параллелепипеда все грани — параллелограммы.

Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные.

Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани ― боковыми гранями параллелепипеда.

Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда. A1 H H1 A2 An A3 B1 B2 n B3 B A B C D A1 B1 C1 D1 7

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.

Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями).

1. Противоположные грани параллелепипеда равны и параллельны.
2. Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Боковые грани прямого параллелепипеда — прямоугольники.
4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Диагонали прямоугольного параллелепипеда равны.

Пирамида

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее.

Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.

Грани, отличные от основания, называются боковыми.

Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины).

Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H.

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины.

Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания.

Свойства пирамиды:

1. Боковые ребра пирамиды равны.
2. Боковые ребра пирамиды одинаково наклонены к основанию пирамиды.
3. Вершина пирамиды проектируется в центр окружности, описанной около основания пирамиды.
4. Высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны, а высота пирамиды лежит внутри пирамиды.
5. Все двугранные углы при основании пирамиды равны.
6. Вершина пирамиды проектируется в центр окружности, вписанной в основание.
7. Высоты всех боковых граней пирамиды, проведённые из вершины пирамиды, равны, а высота пирамиды лежит вне пирамиды.
8. Двугранные углы между боковыми гранями и плоскостью основания пирамиды равны.
9. Вершина пирамиды проектируется в центр окружности, вневписанной в основание пирамиды.

Правильная пирамида

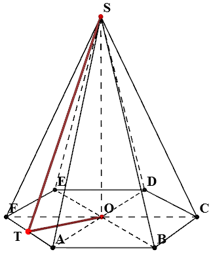
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.

Свойства правильной пирамиды:

1. В правильной треугольной пирамиде противоположные ребра попарно перпендикулярны.
2. Боковые ребра правильной пирамиды равны между собой.
3. Двугранные углы при основании правильной пирамиды равны между собой.
4. Двугранные углы при боковых рёбрах правильной пирамиды равны.

Тетраэдр

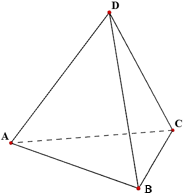
Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.

Тетраэдр называется правильным, если все его грани – равносторонние треугольники.

Свойства тетраэдра:

1. Все ребра правильного тетраэдра равны между собой.
2. Все грани правильного тетраэдра равны между собой.
3. Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.

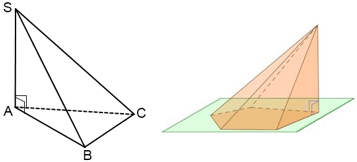
Прямоугольная пирамида

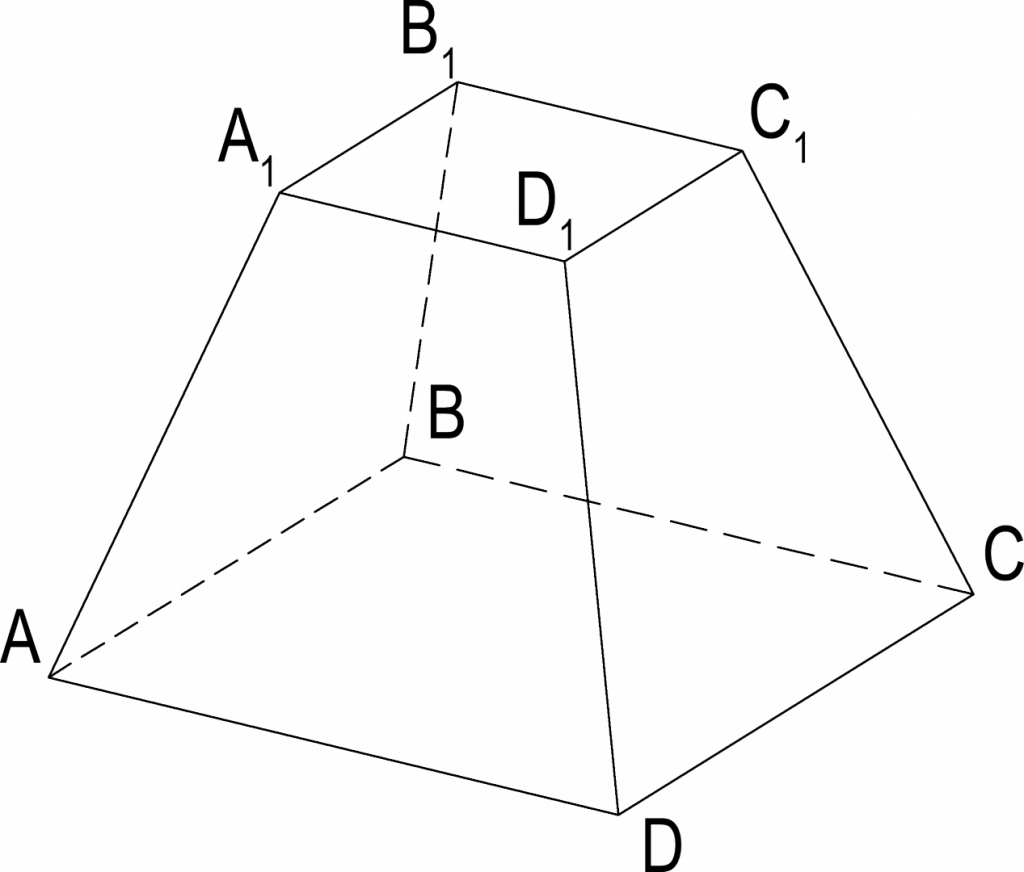
Усечённая пирамида

Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.

Свойства усечённой пирамиды:

1. Основания усечённой пирамиды — подобные многоугольники.
2. Боковые грани усечённой пирамиды — трапеции.
3. Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
4. Боковые грани правильной усечённой пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
5. Двугранные углы при боковых рёбрах правильной усечённой пирамиды равны.

Сфера и шар

Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.

Хордой сферы называется отрезок, соединяющий две точки сферы.

Диаметром сферы называется хорда, проходящая через ее центр. Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.

Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра.

Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.

Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.

Теорема 1: (о сечении сферы плоскостью). Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
Теорема 2: (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.

Доказательство

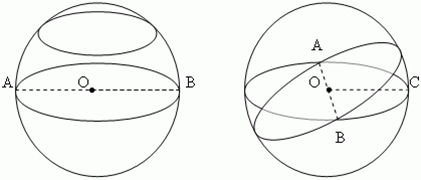
Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.

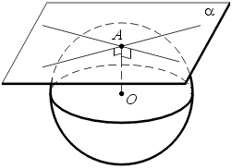
Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.

Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.

Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.

Теорема 1: (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
Теорема 2: (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.

Многогранники

Геометрическим телом (или просто телом) называется ограниченная связная фигура в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры. Границу геометрического тела называют также его поверхностью и говорят, что поверхность ограничивает тело.

Плоскость, по обе стороны которой имеются точки данного тела, называется секущей плоскостью.

Фигура, которая образуется при пересечении тела плоскостью, называется сечением тела.

Многогранником или многогранной поверхностью называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Тело, ограниченное многогранником, часто также называют многогранником.

Многоугольники, из которых составлен многогранник, называют его гранями. Стороны граней называются ребрами, а концы ребер — вершинами многогранника.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

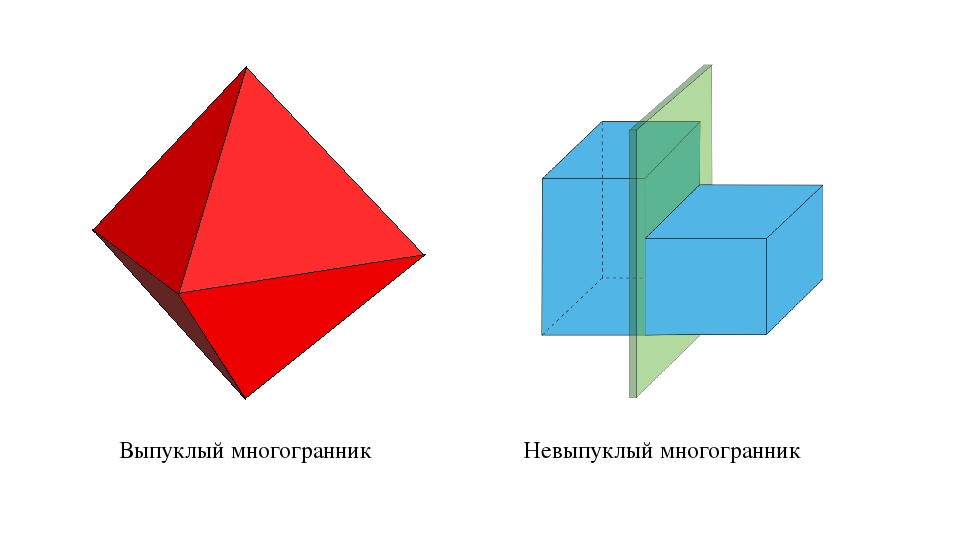
Многогранники бывают выпуклые и невыпуклые.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками.

1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.
3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.
4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.

Правильные многогранники

Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники, и в каждой его вершине сходится одно и то же число ребер.

Все ребра правильного многогранника равны, все двугранные углы правильного многогранника равны, все многогранные углы правильного многогранника равны.

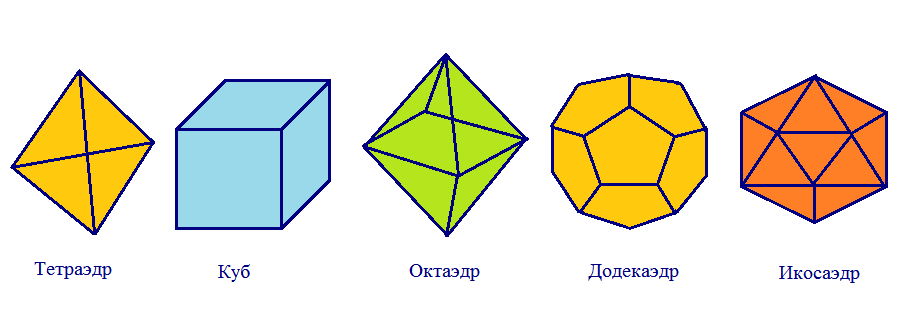
Существует ровно пять выпуклых правильных многогранников:

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, и в каждой вершине многогранника сходится одно и то же число ребер. Все ребра правильного многогранника равны друг другу. Равны также все его двугранные углы, содержащие две грани с общим ребром.

1.Правильный тетраэдр (четырехгранник) ― многогранник, составленный из четырех правильных треугольников.

3. Правильный октаэдр (восьмигранник) ― многогранник, составленный из восьми правильных треугольников.

4. Правильный додекаэдр (двенадцатигранник) ― многогранник, составленный из двенадцати правильных пятиугольников.

5. Правильный икосаэдр (двадцатигранник) ― многогранник, составленный из двадцати правильных треугольников.

Цилиндр

В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности.

Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.

Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.

Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.

Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.

Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.

Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.

Радиусом цилиндра называется радиус его оснований.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.

Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.

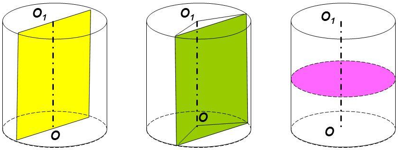
Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.

1. Основания цилиндра равны
2. Основания лежат в параллельных плоскостях
3. Образующие цилиндра параллельны и равны

Источник