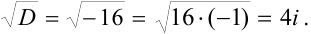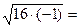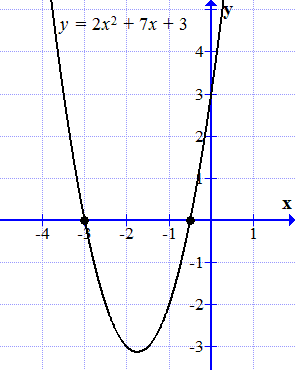В дискриминанте отрицательное число что делать
Решение квадратных уравнений с отрицательным дискриминантом
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример №42.4.
Решить уравнение: 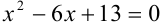
Решение:
Найдем дискриминант: 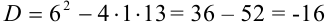
Тогда 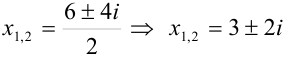
Ответ: 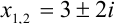
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение 

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Если в дискриминанте отрицательное число
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример 42.4. Решить уравнение: 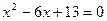
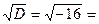
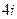
Тогда 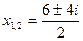
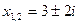
Ответ:
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.
Дата добавления: 2014-12-27 ; Просмотров: 11818 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Как решать квадратные уравнения?
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых.
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
– если (D) положителен – уравнение будет иметь два корня;
– если (D) равен нулю – только один корень;
– если (D) отрицателен – корней нет.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_ ) и (x_ ) будут различны по значению, ведь в первой формуле (sqrt ) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед (sqrt )
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_ =1) и (x_ =-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Оба корня содержат невычислимое выражение (sqrt ), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Дискриминант
Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.
Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt
Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед \(\sqrt
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Находим корни уравнения
Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Если дискриминант отрицательный то сколько корней
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
– если (D) положителен – уравнение будет иметь два корня;
– если (D) равен нулю – только один корень;
– если (D) отрицателен – корней нет.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_ ) и (x_ ) будут различны по значению, ведь в первой формуле (sqrt ) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед (sqrt )
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_ =1) и (x_ =-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
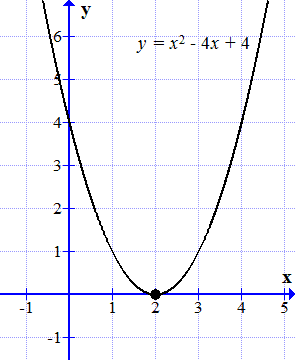
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Оба корня содержат невычислимое выражение (sqrt ), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Как решать квадратные уравнения?
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых.
Основные формулы
Графическая интерпретация
Ниже приводятся примеры таких графиков.
Полезные формулы, связанные с квадратным уравнением
Вывод формулы для корней квадратного уравнения
Выполняем преобразования и применяем формулы (f.1) и (f.3):
Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение
Примеры определения корней квадратного уравнения
Пример 1
Отсюда получаем разложение квадратного трехчлена на множители:
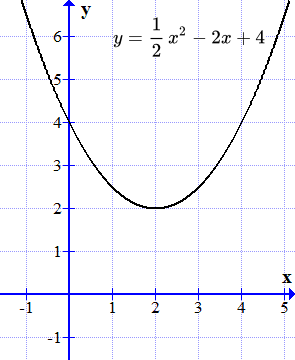
График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.
Пример 2
Тогда разложение трехчлена на множители имеет вид:
.
График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.
Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.
Пример 3
Можно найти комплексные корни:
;
;
.
График функции не пересекает ось абсцисс. Действительных корней нет.
Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.
Действительных корней нет. Корни комплексные:
;
;
.
Решение квадратных уравнений с отрицательным дискриминантом
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример 42.4. Решить уравнение: 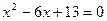
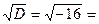
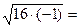
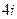
Тогда 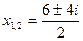

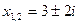
Ответ:
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет