В чем выражается частота
Частота
Единицей измерения частоты в Международной системе единиц (СИ) является герц (русское обозначение: Гц; международное: Hz), названный в честь немецкого физика Генриха Герца.
Частота обратно пропорциональна периоду колебаний: ν = 1/T.
Частота, как и время, является одной из наиболее точно измеряемых физических величин: до относительной точности 10−17.
В природе известны периодические процессы с частотами от
10−16 Гц (частота обращения Солнца вокруг центра Галактики) до
1035 Гц (частота колебаний поля, характерная для наиболее высокоэнергичных космических лучей).
В квантовой механике частота колебаний волновой функции квантовомеханического состояния имеет физический смысл энергии этого состояния, в связи с чем система единиц часто выбирается таким образом, что частота и энергия выражаются в одних и тех же единицах (иными словами, переводный коэффициент между частотой и энергией — постоянная Планка в формуле E = hν — выбирается равным 1).
Глаз человека чувствителен к электромагнитным волнам с частотами от 4⋅1014 до 8⋅1014 Гц (видимый свет); частота колебаний определяет цвет наблюдаемого света. Слуховой анализатор человека воспринимает акустические волны с частотами от 20 Гц до 20 кГц. У различных животных частотные диапазоны чувствительности к оптическим и акустическим колебаниям различны.
Отношения частот звуковых колебаний выражаются с помощью музыкальных интервалов, таких как октава, квинта, терция и т. п. Интервал в одну октаву между частотами звуков означает, что эти частоты отличаются в 2 раза, интервал в чистую квинту означает отношение частот 3⁄2. Кроме того, для описания частотных интервалов используется декада — интервал между частотами, отличающимися в 10 раз. Так, диапазон звуковой чувствительности человека составляет 3 декады (20 Гц — 20 000 Гц). Для измерения отношения очень близких звуковых частот используются такие единицы, как цент (отношение частот, равное 21/1200) и миллиоктава (отношение частот 21/1000).
Частота
Определение частоты
Частотой называют физическую величину, характеризующую периодический процесс.
Частота колебаний
Частота служит одним из основных параметров, характеризующих колебания.
В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами ($<\nu >_1\ и\ <\nu >_2$) равна:
Другой характеристикой колебаний является циклическая частота, которая равна:
Циклическая частота измеряется в радианах, деленных на секунду:
Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.
Частота колебаний физического маятника:
Частота дискретных событий, частота вращения
Единицей измерения частоты дискретных событий является обратная секунда:
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Примеры задач с решением
Решение. Рассмотрим уравнение движения частицы:
Подставим значение циклической частоты, полученное из уравнения (1.1) в формулу (1.3), получаем:
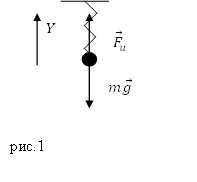
Решение. Сделаем рисунок.
В нашей задаче мы имеем колебания пружинного маятника, частоту которого можно найти как:
Рассмотрим состояние равновесия тела, которое прикреплено к пружине (рис.1). Запишем второй закон Ньютона для сил, действующих на это тело в состоянии равновесия:
Запишем проекцию уравнения (2.2) на ось Y:
Так как колебания груза на пружине малые, то выполняется закон Гука и мы можем считать, что:
\[F_u=k\Delta x\ \left(2.4\right).\]
Подставим полученный в (2.5) результат в (1.1), частота колебаний тела на пружине равна:
Амплитуда, период, частота колебаний.
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
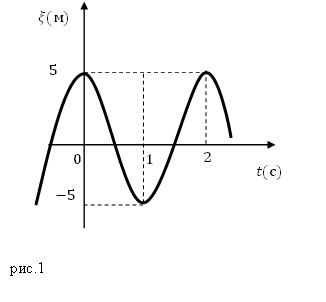
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Формула частоты
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами ($<\nu >_1\ и\ <\nu >_2$) равна:
Еще одно величиной характеризующей колебательный процесс является циклическая частота ($<\omega >_0$), связанная с частотой как:
Циклическая частота измеряется в радианах, деленных на секунду:
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
Физический маятник совершает колебания с частотой:
Формулы для вычисления частоты дискретных событий, частота вращения
Единицей измерения частоты дискретных событий является обратная секунда:
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Примеры задач с решением
Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?
Амплитуда, период, частота колебаний.
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

Циклическая частота — это число колебаний, совершаемых за 2π секунд.