В 1820 году ампер установил что

В 1820 году ампер установил что

Компания ЭТМ запись закреплена

Освежим школьные знания и вспомним о важнейших открытиях в электромагнетизме, а именно об Опыте Эрстеда, силах Ампера и Лоренца. Поможет нам в этом видеоролик, подготовленный компанией EKF.

В 1820 году Ханс Кристиан Эрстед своим экспериментом впервые доказал воздействие электрического тока на магнит, а также заметил, что линии магнитного поля направлены перпендикулярно относительно проводника, по которому протекает ток.

В том же 1820 году Андре Мари Ампер установил, что два параллельных проводника притягиваются друг к другу, если ток в них течет в одном направлении. Силу, которая при этом воздействует на проводники, назвали силой Ампера.

А в 1892 Хендрик Антон Лоренц вывел выражение силы действующий на точечную заряженную частицу, находящуюся в электромагнитном поле.

Мне больше нравятся опыты французского физика Жан-Антуан Нолле. Они намного интереснее. )))

Для тех, кто не знает: Скорость электрического тока почти равна скорости света. В 1746 году, когда это ещё не было известно, французский священник и физик Жан-Антуан Нолле захотел измерить скорость тока экспериментально. Он расставил 200 монахов, соединённых друг с другом железными проводами, по окружности длиной свыше полутора километров, а затем разрядил в эту цепь батарею из лейденских банок, изобретённых годом ранее. Все монахи среагировали на ток в одно мгновение, что убедило Нолле в очень высоком значении искомой величины.

Хороший физик. И опыты у него интересные.

Валерий, а еще скорость перемещения отдельно взятого электрона очень большая, но при этом его скорость перемещния ВДОЛЬ проводника мала, и в принципе не определима.

Ну то есть представим что в точке А в это мгновение сидит себе электрон спокойненько, подёргивается от теплового воздействия, да еще от разных других, которые передают ему определенную энергию, тут вдрог замкнули вы рубильник, да напряжение подали. Электрон тут же сорвется и полетит, но куда он полетит? На другую орбиталь или же к другому атому? Сколько раз он столкнется и будет ли он двигаться в том же направлении? Да он никогда может и не «доползти» до другого конца проводника.

Но в целом скорость электического ТОКА, читайть как ПОТОКА, ДВИЖЕНИЯ — мгновенна.

Как в старом анекдоте про скорость включения лампочки и понос у Вовочки

Источник

Магнитного поля

И Био-Савара-Лапласа. Принцип суперпозиции для

Магнитное поле и его характеристики. Законы Ампера

Все мы слышали слова “магнитное поле”, знаем, что постоянные магниты притягивают металлы, знаем, что стрелка компаса ориентируется вдоль магнитного поля Земли. Сейчас мы более детально познакомимся с тем, что мы называем “магнитное поле”. Итак, учение о магнетизме ведёт своё начало с опытов датского физика Х. Эрстеда, который в 1820 г. обнаружил, что проводник с током оказывает ориентирующее воздействие на магнитную стрелку. Схема опыта Эрстеда показана на рис. 3.1. При включении тока через прямолинейный проводник магнитная стрелка устанавливалась перпендикулярно току. При смене направления тока в проводнике изменялось и направление магнитной стрелки. В том же 1820 г. французский физик Ампер установил, что два параллельных прямых проводника с током, размещённых на некотором расстоянии R друг от друга, притягиваются, если токи в них имеют одинаковое направление, и отталкиваются, если токи в этих проводниках противоположно направлены. Он же установил и формулу силы, приходящейся на единицу длины каждого проводника. Сейчас выражение для этой силы записывается в виде

. (3.1)

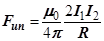
dF = I [d l,B]. (3.2)

Квадратные скобки в формуле (3.2) обозначают векторное произведение. Модуль векторного произведения (3.2) определяется как

где a – угол между векторами dl и B. Здесь же отметим, что направление силы перпендикулярно плоскости, в которой лежат перемножаемые векторы и определяется правилом правого винта для определения направления векторного произведения.

Так как магнитное поле является силовым, то его можно графически изобразить при помощи линий магнитной индукции, касательная к которым в каждой точке совпадает с направлением индукции магнитного поля в этой же точке. Подчеркнём, что основная силовая характеристика магнитного поля – это индукция. В этом смысле индукция магнитного поля аналогична напряжённости электрического поля. Кроме того, имеется и вспомогательная характеристика магнитного поля, которая называется напряжённостью магнитного поля, и эта величина аналогична электрическому смещению для электрического поля. Для однородной изотропной среды связь между напряжённостью и индукцией магнитного поля имеет следующий вид:

. (3.4)

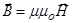
Здесь m – так называемая магнитная проницаемость среды, о которой мы будем говорить позднее.

Из опытов Эрстеда и Ампера следовало, что магнитное поле создаётся электрическими токами. Французские физики Био и Савар попытались установить закон, определяющий связь между током и создаваемым этим током магнитным полем. Они проделали много опытов, собрали большой фактический материал, но не смогли установить искомую зависимость из своих результатов. Тогда они обратились за помощью к тогда уже известному другому французскому учёному Лапласу. Лаплас проанализировал результаты опытов Био и Савара и предложил формулу, которая сейчас называется законом Био-Савара-Лапласа, и которая вместе с принципом суперпозиции для магнитного поля позволяет определить магнитное поле, создаваемое любым проводником в произвольной точке:

. (3.5)

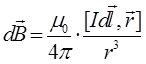
Здесь Idl – произведение силы тока на элементарный вектор dl, совпадающий по направлению с током на данном участке проводника, называется элементом тока, r – вектор, проведенный от элемента тока Idl в точку, где вычисляется магнитная индукция. Рис.3.2 поясняет формулу Био-Савара-Лапласа. Из формулы (3.4) и рис.3.2 видно, что направление магнитного поля связано с направлением тока в проводнике правилом правого винта. Таким образом, вектор магнитной индукции В перпендикулярен плоскости, проходящей через вектор dl и точку, в которой вычисляется магнитная индукция. Чтобы получить индукцию, созданную всем проводником, нужно просуммировать в данной точке магнитные поля, создаваемые каждым элементом тока этого проводника. Если имеется несколько проводников, то необходимо векторно сложить в данной точке магнитные поля, создаваемые каждым проводником в отдельности. Модуль выражения (3.4) определяется как

, (3.6)

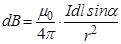
где a – угол между векторами dl и r.

Как уже отмечалось, для магнитного поля, так же как и для электрического, справедлив принцип суперпозиции, который утверждает, что магнитное поле, созданное в некоторой точке несколькими токами, равно векторной сумме полей, создаваемых в этой точке каждым из токов в отдельности:

. (3.7)

Формулу (3.7) можно преобразовать следующим образом

. (3.8)

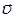
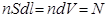
Здесь q – заряд электрона, n – концентрация, – скорость направленного движения электронов в проводнике. Она совпадает по направлению с вектором dl, поэтому мы имеем право в векторном произведении перенести значок вектора с вектора dl на вектор скорости. Мы также воспользовались тем, что сила тока может быть записана как плотность тока, умноженная на площадь поперечного сечения проводника , а также тем, что произведение поперечного сечения проводника на его бесконечно малую длину dl равно элементу объёма dV, а произведение концентрации зарядов на объём равно количеству зарядов в этом объёме N:

. (3.9)

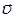
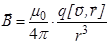
С учётом сделанных замечаний получим индукцию магнитного поля, создаваемого движущимся со скоростью зарядом:

. (3.10)

Необходимо отметить, что формула (3.10) справедлива при условии 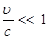, где с – скорость распространения света в вакууме.

Из выражения (3.5) видно, что величина магнитного поля обратно пропорциональна квадрату расстояния до элемента тока, создающего это поле. Вспомним, что и основная силовая характеристика электрического поля – напряжённость электрического поля – также обратно пропорциональна квадрату расстояния до источника этого поля – электрического заряда:

. (3.11)

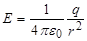
Такая зависимость не является случайной, а отражает глубокую связь между электрическими и магнитными явлениями. В частности, в курсе теоретической физики доказывается, что магнитное взаимодействие токов является следствием закона Кулона и инвариантности заряда. Инвариантность заряда означает, что его величина не зависит от скорости движения заряда. Также доказывается, что электрическое и магнитное поля неразрывно связаны и образуют единое электромагнитное поле. Можно так выбрать систему отсчёта, что магнитное поле будет равно нулю. Этот вывод также следует и из формулы (3.9). Соответственно, также можно выбрать такую систему отсчёта, в которой электрическое поле будет равно нулю. Во всех остальных системах отсчёта будет наблюдаться единое электромагнитное поле, как совокупность электрического и магнитного полей.

Теперь воспользуемся законом Ампера для расчёта силы взаимодействия, приходящейся на единицу длины двух параллельных токов. В самом деле, пусть у нас есть два параллельных проводника, с расстоянием между ними R, по которым в одном и том же направлении текут токи I₁ и I₂ (рис.3.3). Ток I₁ создаёт в месте нахождения второго проводника магнитное поле B₁, и ток I₂ создаёт в месте нахождения первого проводника магнитное поле B₂. По закону Ампера, на элемент тока I₂dl действует сила dF₁=I₂B₁dl. Здесь учтено, что sina=1. На основании формулы (3.14)

.

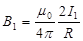
Окончательно, таким образом, получаем, что

. (3.12)

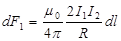
Аналогичным образом можно показать, что

. (3.13)

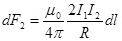
Направления сил указаны на рис. 3.1/3. Таким образом, получили, что два параллельных проводника, по которым текут токи в одном и том же направлении, притягиваются друг к другу с одинаковыми силами, приходящимися на единицу длины этих проводников и задаваемыми формулой (3.1). Если токи направлены в разные стороны, то, рассуждая аналогичным образом, можно показать, что проводники будут отталкиваться с силой, также определяемой формулой (3.1).

Источник

Презентация была опубликована 8 лет назад пользователемИнесса Донцова

Похожие презентации

2 Направление силы Ампера определяется правилом левой руки: четыре пальца левой руки надо направить по направлению тока так, чтобы вектор магнитной индукции входил в ладонь, тогда отогнутый большой палец дает направление силы Ампера. Направление силы Ампера определяется правилом левой руки: четыре пальца левой руки надо направить по направлению тока так, чтобы вектор магнитной индукции входил в ладонь, тогда отогнутый большой палец дает направление силы Ампера.

3 На основе закона Ампера определим силу взаимодействия между двумя параллельными прямыми токами, расположенными на расстоянии d друг от друга. Рассмотрим сначала случай, когда токи текут в одном направлении. Ток I 1 создает магнитное поле B 1, которое действует на ток I 2 и наоборот. На расстоянии d магнитная индукция тока I 1 равна На основе закона Ампера определим силу взаимодействия между двумя параллельными прямыми токами, расположенными на расстоянии d друг от друга. Рассмотрим сначала случай, когда токи текут в одном направлении. Ток I 1 создает магнитное поле B 1, которое действует на ток I 2 и наоборот. На расстоянии d магнитная индукция тока I 1 равна

4 Угол между направлением тока I 2 и вектором магнитной индукции B 1 равен 90º. Поэтому согласно закону Ампера магнитное поле тока I 1 действует на единицу длины тока I 2 с силой (3.4.3) Размерность этой силы Угол между направлением тока I 2 и вектором магнитной индукции B 1 равен 90º. Поэтому согласно закону Ампера магнитное поле тока I 1 действует на единицу длины тока I 2 с силой (3.4.3) Размерность этой силы

5 Аналогично, магнитное поле тока I 2 действует на единицу длины тока I 1 с силой Сравнивая видим, что силы F 21 и F 12 совпадают по величине. Направления этих сил противоположны. Поэтому токи, текущие в одном направлении притягивают друг друга. Если направления токов противоположны, то изменятся направления сил F 21 ( ) и F 12 ( ). Поэтому токи, текущие навстречу друг другу отталкиваются. Аналогично, магнитное поле тока I 2 действует на единицу длины тока I 1 с силой Сравнивая видим, что силы F 21 и F 12 совпадают по величине. Направления этих сил противоположны. Поэтому токи, текущие в одном направлении притягивают друг друга. Если направления токов противоположны, то изменятся направления сил F 21 ( ) и F 12 ( ). Поэтому токи, текущие навстречу друг другу отталкиваются.

7 Теперь можно определить и единицу магнитной индукции В. Пусть элемент проводника dl перпендикулярен вектору магнитной индукции. Тогда согласно (3.4.3) имеем Последняя формула и используется для определения единицы магнитной индукции. Единицей магнитной индукции является Тесла – это магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, перпендикулярного полю и по которому течет ток силой 1 А. Теперь можно определить и единицу магнитной индукции В. Пусть элемент проводника dl перпендикулярен вектору магнитной индукции. Тогда согласно (3.4.3) имеем Последняя формула и используется для определения единицы магнитной индукции. Единицей магнитной индукции является Тесла – это магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, перпендикулярного полю и по которому течет ток силой 1 А.

8 Найдем силу, действующую на движущийся в магнитном поле электрический заряд. Рассмотрим проводник с током I, находящийся в магнитном поле с индукцией В. Пусть за время dt через участок проводника dl проходит dn зарядов величиной q. Тогда ток, текущий через проводник равен Найдем силу, действующую на движущийся в магнитном поле электрический заряд. Рассмотрим проводник с током I, находящийся в магнитном поле с индукцией В. Пусть за время dt через участок проводника dl проходит dn зарядов величиной q. Тогда ток, текущий через проводник равен 3.5 Сила Лоренца

9 Согласно закону Ампера (3.4.2), на этот участок проводника со стороны магнитного поля действует сила Разделив на dn получим силу, действующую на один заряд Согласно закону Ампера (3.4.2), на этот участок проводника со стороны магнитного поля действует сила Разделив на dn получим силу, действующую на один заряд

11 Так как сила Лоренца направлена перпендикулярно к вектору скорости, а следовательно и к вектору перемещения, то она не совершает работы над зарядом. Поэтому постоянное магнитное поле не меняет энергию заряженной частицы. Магнитное поле меняет лишь направление вектора скорости, но не меняет величину скорости. Из формулы (3.5.1) следует, что если заряд неподвижен, то сила Лоренца равна нулю. Поэтому постоянное магнитное поле не оказывает на покоящийся заряд никакого влияния. Так как сила Лоренца направлена перпендикулярно к вектору скорости, а следовательно и к вектору перемещения, то она не совершает работы над зарядом. Поэтому постоянное магнитное поле не меняет энергию заряженной частицы. Магнитное поле меняет лишь направление вектора скорости, но не меняет величину скорости. Из формулы (3.5.1) следует, что если заряд неподвижен, то сила Лоренца равна нулю. Поэтому постоянное магнитное поле не оказывает на покоящийся заряд никакого влияния.

12 Если, то частица будет двигаться по окружности, радиус которой определяется из 2-го закона Ньютона Откуда (3.5.2) Если, то частица будет двигаться по окружности, радиус которой определяется из 2-го закона Ньютона Откуда (3.5.2)

14 Б) В фазотроне (синхроциклотроне) – нарушение синхронизма компенсируется уменьшением частоты электрического поля Е В) В синхротроне – синхронизация обеспечивается за счет изменения магнитной индукции так, чтобы m/B = const. Его используют для ускорения только электронов. Г) В протонном синхротроне (синхрофазотроне) – синхронизация обеспечивается изменениями Е и В так, чтобы радиус оставался постоянным и траектория была не спиралью, а окружностью. Энергия протонов достигает 76 МэВ. В ТПУ электронный синхрофазотрон Сириус разгоняет электроны до скорости v = c, при этом они имеют энергию 950 МэВ. Б) В фазотроне (синхроциклотроне) – нарушение синхронизма компенсируется уменьшением частоты электрического поля Е В) В синхротроне – синхронизация обеспечивается за счет изменения магнитной индукции так, чтобы m/B = const. Его используют для ускорения только электронов. Г) В протонном синхротроне (синхрофазотроне) – синхронизация обеспечивается изменениями Е и В так, чтобы радиус оставался постоянным и траектория была не спиралью, а окружностью. Энергия протонов достигает 76 МэВ. В ТПУ электронный синхрофазотрон Сириус разгоняет электроны до скорости v = c, при этом они имеют энергию 950 МэВ.

15 В 1879 году Холл обнаружил, что в металлической пластине, находящейся в магнитном поле, возникает поперечное электрическое поле, перпендикулярное направлению тока и вектору магнитной индукции. Рассмотрим тонкую металлическую пластину толщиной а и шириной d. Пусть по пластине течет ток с плотностью j. Магнитное поле В направлено перпендикулярно к боковой грани. В 1879 году Холл обнаружил, что в металлической пластине, находящейся в магнитном поле, возникает поперечное электрическое поле, перпендикулярное направлению тока и вектору магнитной индукции. Рассмотрим тонкую металлическую пластину толщиной а и шириной d. Пусть по пластине течет ток с плотностью j. Магнитное поле В направлено перпендикулярно к боковой грани. 3.6 Эффект Холла

16 Электроны под действием силы Лоренцаприжимаются к верхней пластине, поэтому на ней возникает избыток отрицательного заряда. На нижней пластине, напротив, будет недостаток электронов. В результате появляется поперечное электрическое поле – поле Холла Е холл. Поле Холла действует на электроны противоположно силе Лоренца. Поэтому через короткое время устанавливается стационарное распределение зарядов в поперечном направлении – вдоль толщины (высоты) пластины. Этому равновесному состоянию отвечает равенство электрической силы со стороны поля Холла и силы Лоренца Электроны под действием силы Лоренцаприжимаются к верхней пластине, поэтому на ней возникает избыток отрицательного заряда. На нижней пластине, напротив, будет недостаток электронов. В результате появляется поперечное электрическое поле – поле Холла Е холл. Поле Холла действует на электроны противоположно силе Лоренца. Поэтому через короткое время устанавливается стационарное распределение зарядов в поперечном направлении – вдоль толщины (высоты) пластины. Этому равновесному состоянию отвечает равенство электрической силы со стороны поля Холла и силы Лоренца

19 Найдем в качестве примера циркуляцию магнитного поля, создаваемого прямым током. Выберем вокруг тока замкнутый контур в плоскости, перпендикулярной к току. В каждой точке контура вектор магнитной индукции направлен по касательной к окружности c радиусом R и проходящей через выбранную точку. Поэтому можем записать Найдем в качестве примера циркуляцию магнитного поля, создаваемого прямым током. Выберем вокруг тока замкнутый контур в плоскости, перпендикулярной к току. В каждой точке контура вектор магнитной индукции направлен по касательной к окружности c радиусом R и проходящей через выбранную точку. Поэтому можем записать

20 Поскольку для прямого тока то Поэтому циркуляция вектора В по замкнутому контуру L равна На контуре L угол меняется от 0 до 2, поэтому (3.7.2) Поскольку для прямого тока то Поэтому циркуляция вектора В по замкнутому контуру L равна На контуре L угол меняется от 0 до 2, поэтому (3.7.2)

21 Полученная формула (3.7.2) справедлива для контура произвольной формы, охватывающего проводник с током. Знак циркуляции зависит от направления обхода. Если направление обхода образует с направлением тока правовинтовую систему, то циркуляция считается положительной, иначе – отрицательной. Знак циркуляции можно учесть, считая ток I алгебраической величиной : ток считается положительным, если его направление связано с направлением обхода по правилу правого винта, иначе – ток считается отрицательным. Полученная формула (3.7.2) справедлива для контура произвольной формы, охватывающего проводник с током. Знак циркуляции зависит от направления обхода. Если направление обхода образует с направлением тока правовинтовую систему, то циркуляция считается положительной, иначе – отрицательной. Знак циркуляции можно учесть, считая ток I алгебраической величиной : ток считается положительным, если его направление связано с направлением обхода по правилу правого винта, иначе – ток считается отрицательным.

22 Если контур не охватывает ток, то при обходе по контуру радиальная прямая сначала поворачивается по часовой стрелке (участок 1-2 ), а затем – против часовой стрелки (участок 2-1 ). Поэтому при полном обходе такого контура угол не меняется и значит циркуляция вектора В равна нулю. Если контур не охватывает ток, то при обходе по контуру радиальная прямая сначала поворачивается по часовой стрелке (участок 1-2 ), а затем – против часовой стрелки (участок 2-1 ). Поэтому при полном обходе такого контура угол не меняется и значит циркуляция вектора В равна нулю.

24 Сравнивая (3.7.3) с формулой для циркуляции вектора напряженности электрического поля видим, что в отличие от электрического поля, циркуляция магнитного поля по замкнутому контуру не равна нулю. Это является следствием вихревого характера магнитного поля. Сравнивая (3.7.3) с формулой для циркуляции вектора напряженности электрического поля видим, что в отличие от электрического поля, циркуляция магнитного поля по замкнутому контуру не равна нулю. Это является следствием вихревого характера магнитного поля.

Источник