В 10 11 заданиях доказать что abcd параллелограмм
Найти координаты точки пересечения его диагоналей.
Координаты проекций на оси длина
длина всех сторон 10
свойство параллелограмма : противоположные стороны попарно равны
Xm = (Xa + Xc) / 2 = (8 + 10) / 2 = 9
Найти площадь параллелограмма, если площадь треугольника ABO равна 7, 5 см.
Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
Дан параллелограмм АВСD
Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
Точка пересечения диагоналей четырехугольника ВСКМ не является середингй одной из них?
Точка пересечения диагоналей четырехугольника ВСКМ не является середингй одной из них.
Может ли этот четырехугольник быть параллелограммом?
Помогите пожалуйста решить?
Помогите пожалуйста решить.
Даны координаты вершин четырёхугольника ABCD.
Доказать что четырехугольник параллелограмм.
Решение основных задач по теме «Параллелограмм»
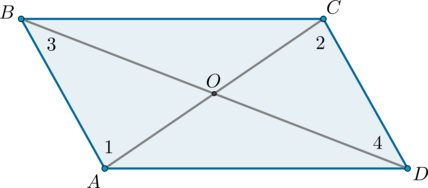
По данным на рисунке докажите, четырёхугольник ABCD является параллелограммом.
Так как B СА= CAD и они являются накрест лежащими при секущей АС, то прямые AD и ВС параллельны.
Имеем две стороны AD и BC четырёхугольника равны и параллельны, значит ABCD является параллелограммом.
Дано: ABCD — параллелограмм; AB : BC = 4 : 5 см; P ABCD = 10,8 см. Найти : AB; BC,CD,AD
Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Пусть меньший угол параллелограмма равен х, тогда больший угол будет равен (х + 40). Поскольку сумма односторонних углов равна 180 градусов, то составим уравнение:
Таким образом, наименьший угол параллелограмма равен 70°.
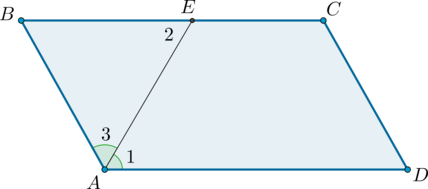
Дано: ABCD — параллелограмм; AC — диагональ; ∠ BAC = 35°; ∠ CAD = 25°. Найти: ∠ A; ∠ B; ∠ C; ∠ D.
Дано: ABCD — параллелограмм; P ABCD = 10 см; P ABD = 8 см. Найти: BD.
Дано: ABCD — параллелограмм; AK — биссектриса ∠ A; BK : KC = 2 : 1; P ABCD = 50 см. Найти: AB; BC; CD; A
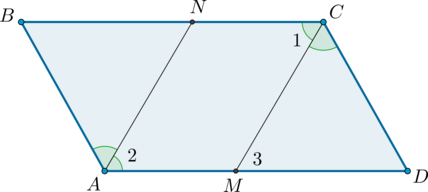
По данным на рисунке докажите, четырёхугольник ABCD является параллелограммом.
В четырёхугольнике диагонали AC и BD пересекаются и делятся точкой пересечения пополам, значит ABCD является параллелограммом.
Решение. 1. В прямоугольном треугольнике KL Е есть угол в 30° ( KL Е=180°-90°-60°=30°), значит катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, то есть K Е=2:2=1см
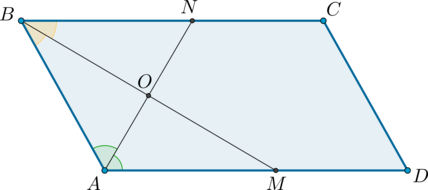
Докажите, что биссектрисы односторонних углов параллелограмма – перпендикулярны.
Пусть А=2х, а D =2у. А и D – односторонние, значит их сумма равна 180°. Поэтому 2х+2у=180 или х+у =90.
Так как А N и DM – биссектрисы, то NAD =х, а MDA =у. По свойству суммы углов треугольника имеем: А OD = 180-(х+у) =180-90=90. А это значит, что прямые А N и DM – перпендикулярны.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Данный материал предназначен для самостоятельного изучения. Например, учащийся заболел. Как разобраться ему в этой теме, каким образом узнать основные типы задач? Или данный материал можно использовать в качестве подготовки к контрольной работе. ссылку на этот материал можно зашифровать куер кодом, что даст возможность изучить в любое время.
Номер материала: ДБ-716210
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Хабаровске родители смогут заходить в школы и детсады только по QR-коду
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
Минздрав включил вакцинацию подростков от ковида в календарь прививок
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Геометрия. 8 класс
Укажите правильный ответ.
Посмотрите на свойство параллелограмма, представленного схематично, и укажите соответствующий ему признак параллелограмма.
Если две противоположные стороны четырёхугольника равны и параллельны,
то этот четырёхугольник – параллелограмм.
Если диагонали четырёхугольника делятся точкой пересечения пополам,
то этот четырёхугольник – параллелограмм.
Если противоположные стороны четырёхугольника попарно равны,
то этот четырёхугольник – параллелограмм.
Укажите правильный ответ.
Посмотрите на свойство параллелограмма, представленного схематично, и укажите соответствующий ему признак параллелограмма.
ABCD – параллелограмм, тогда ∠A + ∠D = 180° и AB = CD
Если диагонали четырёхугольника делятся точкой пересечения пополам,
то этот четырёхугольник – параллелограмм.
Если противоположные стороны четырёхугольника попарно равны,
то этот четырёхугольник – параллелограмм.
Если две противоположные стороны четырёхугольника равны и параллельны,
то этот четырёхугольник – параллелограмм.
Укажите правильный ответ.
Посмотрите на свойство параллелограмма, представленного схематично, и укажите соответствующий ему признак параллелограмма.
Если две противоположные стороны четырёхугольника равны и параллельны,
то этот четырёхугольник – параллелограмм.
Если противоположные стороны четырёхугольника попарно равны,
то этот четырёхугольник – параллелограмм.
Если диагонали четырёхугольника делятся точкой пересечения пополам,
то этот четырёхугольник – параллелограмм.
Укажите верные ответы.
Дан четырёхугольник ABCD, AB = CD, BD – диагональ, причём ∠ABD = ∠CDB.
Что можно найти / доказать по данным условиям?
Доказать, что ABCD – параллелограмм.
Найти углы B и D четырёхугольника ABCD.
Найти сумму углов четырёхугольника ABCD, прилежащих к одной стороне.
Найти углы A и C четырёхугольника ABCD.
Доказать, что равны треугольники ABD и CDB.
Параллелограмм
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Итак, в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник \(ABCD\) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
2) Пусть \(ABCD\) – параллелограмм, \(AN\) и \(BM\) – биссектрисы углов \(BAD\) и \(ABC\) соответственно.