тренажер для быстрого счета в уме
Тренажер устного счета
Данный тренажер является одним из тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.
Онлайн тренажер устного счета
Принцип работы основан на генерации примеров по математике подходящего вам уровня сложности для всех классов, решение которых способствует развитию навыков устного счёта.
Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.
Разнообразие режимов
На странице настроек режима можно задавать необходимые параметры генерации примеров по математике для любого класса.
Тренажер устного счета позволяет отрабатывать 4 небезызвестных арифмитических действия на шести уровнях сложности.
Далее корректируете вид математического примера выбирая тип, устанавливая количество слагаемых, манипулируя числовыми множествами.
На данном этапе разработки были продуманы и реализованы режимы, позволяющие работать с двумя множествами чисел: Положительными и Отрицательными. В каждом из ним можно попрактиковаться в различных типах заданий: «Пример», «Уравнение», «Сравнение».



Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». А когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.
Бонусом является возможность загрузить и в дальнейшем распечатать «самостоятельную работу» в формате PDF, состоящую из 26 примеров соответствующего режима, кликнум по значку Принтер.
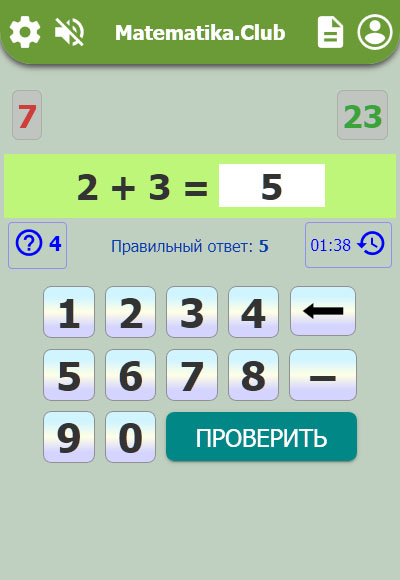
Процесс счёта
Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звковые уведомления или перейти к Протоколу ошибок и подсказок.
Вы решаете заданый пример, вводите ответ с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки результат Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.
Если по какой-либо причине вы хотите обнулить свои результаты, нажмите на иконку «Сбросить результат» спарва.
Игровая форма
Приложение также предусматривает игровую анимацию «Сражение фехтовальщиков».
Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.
Если режим с анимацией вам мешает, его можно отключить на странице установок с помощью иконки
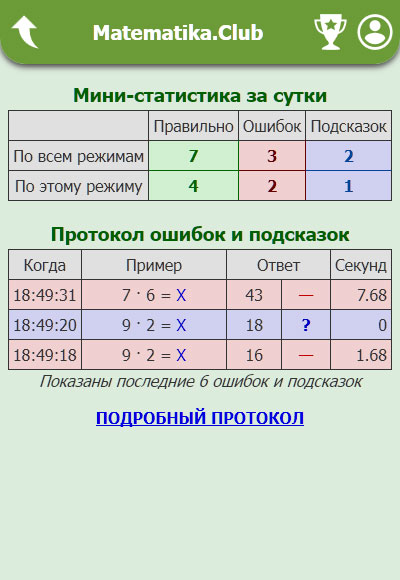
Протокол ошибок
В любой момент работы с тренажером вы можете перейти к разделу приложения «Протокол ошибок», кликнув на соответствующую иконку сверху, либо перелестнув страницу вниз.
Здесь вы сможете посмотреть свою статистику (количество примеров по категориям) за последние сутки и по последнему режиму.
А также увидеть список ошибок и подсказок (максимум 6 штук), либо перейти к подробной статистике.
Дополнительная информация
Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:
домен сайта + раздел приложения + кодировка данного режима
например: matematika.club/app/#12301
Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.
Тренажёр устного счёта
Онлайн-тест для проверки знания таблицы умножения и навыков устного счёта. Выберите арифметическое действие, кол-во вопросов в тесте и приступайте к проверке навыков сложения, вычитания, деления или умножения.
Кол-во вопросов в тесте
Тренируйте устный счёт эффективно
Тренажёр устного счёта предназначен для проверки знания таблицы умножения и тренировки вычислительных навыков: умения складывать и вычитать, делить и умножать. Тренажёр развивает память, концентрацию и скорость реакции, помогает ученикам начальной школы довести навыки устного счёта до автоматизма, а старшеклассникам — быстро освежить в памяти таблицу умножения перед школьной контрольной или экзаменом.
Учитесь всерьёз и надолго
Для облегчения запоминания вопросов в тренажёре на Блицтесте реализована система умного повторения — эффективный способ запоминания информации. Система включается автоматически для авторизованных пользователей. Просто выбирайте цель и приступайте к учёбе.
Таблица умножения
Сложение в пределах от 10 до 20
Сложение в пределах 10
Сложение в пределах 20 с переходом через десяток
Повышайте успеваемость в школе
Регулярные тренировки в тренажёре развивают навыки устного счёта и гарантируют рост успеваемости по математике в школе.
Задача математики в начальной школе — научить детей решать примеры на четыре арифметических действия: сложение, вычитание, умножение и деление. Школа учит детей считать письменно, но не менее важно развивать навыки устного счёта. В тренажёре удобно учить умножение и деление в пределах 100 и практиковаться в устном счёте в рамках программы математики начальной школы. Режимы повышенной трудности помогут старшеклассникам закрепить вычислительные навыки, необходимые при решении задач по геометрии и тригонометрии.
Базовый курс математики
Тренажёр устного счёта развивает математические навыки, а курс «Математика начальной школы» даёт конкретные математические знания. В курсе сформулированы основополагающие термины и правила, без которых немыслимо изучение математики старших классов:
Развивайте память и концентрацию
В жизни мы ежедневно сталкиваемся с задачами, требующими быстрого решения. Продавец взвесил яблоки и назвал стоимость. Если он ошибся, у нас есть несколько секунд, чтобы его поправить, прежде чем оплатить покупку. Онлайн-тренажёр устного счёта развивает скорость реакции, тренирует память и концентрацию, позволяет довести навыки устного счёта до автоматизма.
Тренируйте только нужное
Выбирайте в Тренажёре устного счёта нужные арифметические действия и один или несколько множителей, делителей, слагаемых или вычитаемых. Используйте настройки тренажёра для тренировки устного счёта с заданным числом, прохождения полного теста по таблице умножения, решения примеров повышенной сложности с отрицательными числами или устного счёта с большими числами.
Опирайтесь на подсказки
Тренажёр устного счёта не только удобный инструмент контроля знаний, но и надёжный помощник в освоении и развитии математических навыков. По ходу онлайн-теста тренажёр выводит для каждого примера подсказки: состав числа или конкретные математические выражения, дополняющие пример.
Регулируйте сложность примеров
Тренируйте сложение и вычитание в пределах двадцати или включите режим «Большие числа» и считайте в пределах ста с переходом через десятки. Регулируйте трудность примеров на умножение и деление: оставайтесь в рамках таблицы умножения или умножайте и делите в т.ч. и на двузначные числа. Используйте переключатель «Отрицательные числа» для добавления в примеры чисел меньше нуля.
Учитесь играючи!
Развивающие и образовательные игры — сила. Фокусировка внимания и позитивная мотивация в игре гарантируют крепкое усвоение материала.
Мы позаботились о простоте и удобстве тренажёра для детей и постарались оптимизировать его для мобильных устройств и планшетов. Для самых маленьких пользователей, которым сложно сохранять концентрацию, мы сделали возможность ограничить тест пятью вопросами и добавили в тренажёр космонавта, звёздочки, звуки, анимацию и конфетти.
Тренажёр устного счёта — бесплатный сервис, но в него вложено огромное количество усилий и средств. Поддержите нас — станьте частью Блицтеста!
Александр Мартынов
Руководитель Блицтеста
Тренажер : Арифметика
Категории тренажеров:
Популярные тренажеры:
Порекомендовать друзьям:
- Увеличивает скорость мышления Концентрирует внимание Логическое мышление
Тренироваться
1769 KS: 48
Самый разнообразный из математических тренажеров для ума, тем самым и более сложный, так как включает в каждом примере минимум две операции в уме, порядок которых также важен и определяется игроком.
Подобные игры для мозга не редкость среди многих культур, однако, выход и в онлайн-платформу Мозготрен, позволил сделать нагрузку более гибкой и разнообразить задания. Также дополнительного азарта тренировкам придает возможность состязаний в режиме реального времени, пригласив друзей померяться силами.
Что тренирует
Арифметический тренажер не является узкоспециализированным, та как он одновременно включает в работу несколько систем нашего мозга. Примеры включают несколько операций и отличаются необходимостью хорошо напрячь мозг. В данном тренажере вы будете тренировать счет в уме: сложение, вычитание, умножение и деление.
Оперативная и кратковременная память – увеличение количества знаков в числах, а также необходимость выполнить несколько расчетов в уме даже на минимальных настройках сложности, требуют хорошего развития оперативной и кратковременной памяти, тем самым данные действия стимулируют этот процесс. Благо, такое место в нашем мозгу не имеет постоянного ограничения и расширяется упражнениями.
Логическое мышление – важное отличие данного тренажера от подобных в разделе заданий на мышление в том, что среди нескольких операций с числами в каждом примере, нужно определять их приоритет, соответственно законам математики. К тому же, выбор правильного алгоритма действий может повлиять на скорость поиска правильного ответа и на результат в целом.
Скорость мышления – посредством многократных выполнений операций с числами, центральная нервная система «приучается» к быстрому повторению подобных действий. Чем больше игрок считает в уме, тем скорее он будет это делать в дальнейшем.
Внимание – это задание требует концентрации не только при поиске нужной ячейки с ответом, но и в ряде случаев с усложнениями, такими как переворот или отрицательные числа. Не менее важно быть внимательным при выполнении нескольких математических операций подряд, учитывая тот факт, что отрицательные ответы могут встречаться даже на самом легком уровне.
Правила
Для настройки сложности, установите разрядность чисел, это может быть число от 3 до 5. Данный параметр указывает сколько чисел будет участвовать в каждом примере для вычисления. Размер каждого числа не зависит от этого условия, они будут увеличиваться с ростом уровня сложности (после каждого правильного ответа). Разрядность чисел значительно влияет на коэффициент сложности – число, отображенное в верхнем левом углу рабочего поля.
Переворот – усложнение, которое меняет пространственное положение примеров. Перевернутые примеры воспринимаются тяжелее для нашего мозга, и это требует больше драгоценного времени, поэтому и коэффициент сложности при включении данного параметра вырастет.
Отрицательные – как очевидно из названия, в примерах будут появляться отрицательные числа, что сделает процесс подсчета интереснее и сложнее. Заметьте, в ответах отрицательные числа могут присутствовать даже на самых легких настройках.
Кнопка рестарт позволяет быстро начать тренировку заново, при этом сохраняться все выбранные ранее настройки сложности.
Начисление очков
Для удобного отслеживания результатов каждой тренировки, по ее окончании вам начисляется соответствующее число баллов, основанных на нескольких важных показателях.
Формула начисления баллов за правильный ответ выглядит так:
Ваша сумма очков + КС*Уровень
КС – коэффициент сложности, он зависит от настроек сложности выбранных до начала теста, эту цифру вы сможете увидеть в верхнем левом углу рабочего поля. При усложнении настроек повышается коэффициент сложности.
Уровень – это не постоянная величина, в начале тренировки он имеет минимальное значение и растет на одну позицию с каждым правильным ответом. При неправильном ответе, уровень стает ниже на позицию.
Формула вычитания баллов за неправильный ответ выглядит так:
Ваша сумма очков – (КС*Уровень)/2
При этом в минусовые значения сумма очков не заходит.
Мульти-игра
Для более интересного прохождения тренировки, всегда есть возможность пригласить друзей и устроить состязание. Для этого, после выбора настроек сложности, в разделе мульти-игра нужно поделиться ссылкой с друзьями, скопировав ее или нажав иконку необходимой соцсети.
Соревнование можно начинать после того, как все игроки подтвердят свою готовность (кнопка «Готов к игре»).
Примеры для всех играющих будут появляться одновременно, для получения баллов, необходимо дать правильный ответ первым. При этом задание обновится, и остальные участники вынуждены будут считать уже новый пример.
Если первый игрок нажал неверный ответ, задание останется на экранах пока соперник не ответит правильно или не правильно.
В верхнем левом углу рабочего поля вы сможете отслеживать текущее количество баллов у вас и у соперника. Зеленый цвет вашего счета подсказывает, что вы лидируете, а красный говорит об отставании.
Результаты соревнований будут занесены в таблицу личных достижений на mozgotren.ru, и отобразятся в графике тренировок на ряду с остальными занятиями.
Как научиться считать в уме
Считать в уме, по мнению многих, в наше время уже неактуально, ведь калькулятор есть в каждом смартфоне, компьютере и ноутбуке. Однако калькулятор не будет сопровождать вас при каждом вашем шаге, а считать необходимо постоянно и много. Способность сосчитать в уме – умение весьма нужное даже в 21 веке. А тем более это нужно школьникам для решения примеров по математике из нелёгкой школьной программы. И им весьма полезно будет уметь считать быстро, не пребегая к электронным устройствам.
Опыт и постоянные тренировки играют важную роль в развитии любых способностей, но навык устного счета не состоит только лишь из опыта. Это могут доказать люди, умеющие считать в уме гораздо более сложные примеры: например, умножать и делить трех- и четырехзначные числа, находить суммы и разности огромных примеров.
Что необходимо знать и делать человеку, дабы повторить такое?
• Во-первых, концентрация или же умение ненадолго удерживать в памяти несколько вещей одновременно.
• Во-вторых, алгоритмы, специальные методы вычислений и математические уловки, значительно облегчающие процесс устного счёта.
• В-третьих, практика. Постоянные тренировки и постепенное усложнение решаемых задач позволят улучшить скорость и качество устного счета.
Важно отметить, что именно практика имеет наибольшее значение. Не обладая достаточным опытом, вы не сможете быстро применять удобные алгоритмы, подходящие под определённые ситуации. И помните, что максимальный эффект будет достигнут при оптимальном использовании всех трёх составляющих. Тренировать сразу все аспекты этого навыка Вы можете в онлайн тренажере устного счёта.
Внимание и концентрация
Чтобы максимально быстро считать в уме, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Существует несколько способов улучшить свою внимательность и способность к концентрации:
При счете в уме, важно ясно представлять себе решаемый пример – визуализировать его. Запоминать промежуточные результаты нужно не на слух, а так как они выглядят в записи, например, на бумаге. Тренировать подобное восприятие можно разными способами, и отчасти визуализация решения приходит с опытом.
Старайтесь всегда находить что-то интересное в рутине, превращая действие в игру. Так поступают и некоторые родители, желающие, чтобы их ребёнок выполнил какую-либо скучную работу.
Огромное количество людей всегда хотят «быть лучше» соперника. Именно поэтому состязательность является еще одним способом развить свою внимательность. В устном счете Вы можете найти себе соперника и пытаться его в этом превзойти.
Еще одним фактором, создающим азарт при счете, может стать борьба с самим собой при достижении определенного результата, то есть личные рекорды. Их можно ставить, например, в скорости счета, в количестве решенных примеров и своей точности ответов.
Наконец, максимальная концентрация может быть достигнута при спонтанном увлечении процессом счета. Как пример, во время чтения Вы перестаёте думать об окружающих вас предметах, людях, ситуациях, полностью погружаетесь в книгу. Именно неподдельный интерес к чему-либо способен заставить вас приобрести наибольшую внимательность в этом деле.
Безусловно, все эти способы надо отрабатывать, практиковать. В этом могут помочь различные тренажеры зрительной памяти и улучшения внимательности.
Простые арифметические закономерности
Решение любой по сложности задачи всегда сводится к применению базовых принципов, и именно эти принципы и закономерности позволят вам быстро выполнять различного рода операции. Существует определенный набор таких правил и закономерностей, которые необходимо довести до автоматизма с помощью разных онлайн тренажеров по математике.
Таблица умножения. Для быстрого устного счета хорошо бы безупречно знать таблицу умножения, которая является основой счета. Если у Вас с этим еще проблемы, можете воспользоваться онлайн Тренажером таблицы умножения.
Деление на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198 + 2 ) на 2 и отнять 2 деленое на 2. Итого: 198 : 2 = 200 :2- 2 :2=100-1=99.
Деление и умножение на 4 и 8. Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно. Например, 46 × 4 = 46 × 2×2 = 92 × 2 =184.
Умножение на 11. Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23×11= 2 (2+3) 3 = 2 5 3. Или если сумма чисел в центре дает результат больше 10: 29×11 = 2 (2+9) 9 = 2 (11) 9 = 3 1 9.
Более сложные методики
Эффективность умножения в уме некоторых двузначных чисел может быть выше за счет меньшего количества действий, если использовать специальные алгоритмов. Ниже представлены три специальные методики, в том числе введение и использование опорного числа.
Квадрат суммы и квадрат разности
23 2 = (20+3) 2 = 20 2 + 2×3×20 + 3 2 = 400+120+9 = 529
69 2 = (70-1) 2 = 70 2 – 70×2×1 + 1 2 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
25 2 = (2×(2+1)) 25 = 625
85 2 = (8×(8+1)) 25 = 7 225
155 2 = (15×(15+1)) 25 = (15×16)25 = 24 025
Опорное число
Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. А методика использования этого числа зависит от того, являются ли множители больше или меньше него самого.
Оба множителя больше опорного. Действовать нужно точно так же, но не вычитать недостаток, а прибавлять избыток:
Один множитель меньше, другой больше опорного. Схема та же, но произведение недостатка и избытка нужно вычитать:
В заключение
Эффективный счёт в уме или разминка для мозга
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
Теперь не кажется невозможным умножить в уме 625 на 53:
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,
В общем случае (M — двузначное число):
Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:
Тогда предыдущий пример можно вычислить немного проще:
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».