считает проценты в уме проект цикада
Что такое ментальная арифметика и как ей научиться
Об эксперте: Анастасия Кузнецова, методист онлайн-школы «Фоксфорд», автор и преподаватель курсов повышения квалификации по ментальной арифметике.
Что такое ментальная арифметика
Попробуйте за несколько секунд решить пример без черновика и калькулятора:
Дети решают такие задачи в уме с помощью ментальной арифметики. Это система развития интеллекта, построенная на обучении устному счету.
Современные родители часто рассказывают о неразвитом воображении и фантазии у ребенка. Дело в том, что мы тренируем левое полушарие мозга ребенка — оно отвечает за логику и математические способности, — но очень мало развиваем правое. Правое полушарие мозга распознает сложные визуальные и звуковые образы. Отвечает за концентрацию внимания и воображение. От гармоничного развития двух полушарий мозга ребенка зависят его когнитивные способности [1].
Ментальная арифметика — это способ развития детского интеллекта с помощью быстрого счета в уме. Сначала ребенок учится считать на счетах-абакус и тренирует мелкую моторику рук. Затем счеты убирают, ребенок представляет их в голове — считает ментально. Развивает воображение и креативность.
Ментальная арифметика помогает комплексно развивать интеллектуальные способности. Моментальный устный счет — приятное дополнение.
Овладев ментальной арифметикой, ребенок намного легче справляется с любой интеллектуальной и творческой работой. Он умеет быстро решать задачи и применять к ним нестандартный подход.
История возникновения ментальной арифметики
Ментальную арифметику придумали около 5 тыс. лет назад. Методикой пользовались в Древней Греции, Индии и Риме, чтобы научить детей считать. В ее основе — умение вычислять на древних счетах-абакус.
Со временем счеты доработали до калькулятора, в 1993 году сформулировали понятие «ментальной арифметики». Сегодня ментальную арифметику используют в 50 странах мира. В Японии и Китае она стала частью школьной программы.
Польза ментальной арифметики
Умение быстро вычислять в уме — не конечная цель. В момент отказа от работы с реальными счетами-абакус правое полушарие мозга начинает работать активнее. В это же время дети развивают логическое мышление и счет, за которые отвечает левое полушарие.
Усиленная работа обоих полушарий мозга становится привычкой и помогает ребенку креативнее решать жизненные задачи. Концентрироваться, смотреть на проблему шире и строить логические цепочки для ее решения. Еще один плюс — развитие сразу нескольких видов памяти: долговременной, кратковременной и фотографической.
Что ученые думают о ментальной арифметике
Американские исследователи проверяли влияние ментальной арифметики на интеллектуальные способности учеников первых и вторых классов в течение года [2]. Результаты получились неоднозначными — первоклассники не справлялись с устным счетом, ребята из второго класса учились лучше, но ученые не выявили заметного улучшения когнитивных способностей.
В 2016 году психолог Дэвид Барнер группой ученых провел подобное исследование в Индии, но за детьми наблюдали уже в течение трех лет [3]. Ментальная арифметика помогла некоторым школьникам лучше учиться, но результат может зависеть и от способностей конкретного ученика. В большинстве других исследований тоже проверяли навыки арифметики. Достаточного количества данных о том, как ментальная арифметика влияет на когнитивные способности, пока нет, поэтому выводы делать рано.
Когда и где учиться ментальной арифметике
Самый подходящий возраст для обучения — от 4 до 12-14 лет. В это время мозг развивается интенсивнее, чем в другие периоды взросления. После 12-14 лет способность мозга приобретать и использовать сложные навыки в таком количестве и темпе снижается.
Сейчас набирают популярность занятия ментальной арифметикой с пожилыми людьми. Такая тренировка мозга — отличный метод профилактики болезней, связанных с памятью и концентрацией внимания.
Самостоятельное обучение может стать непростой задачей. Учеба требует усидчивости, внимательности и разнообразные форматы занятий. Чтобы правильно обучить ребенка ментальной арифметике, лучше обратиться к квалифицированному педагогу.
Как выбрать школу или курс ментальной арифметики
Чтобы выбрать подходящую школу ментальной арифметики для ребенка, проверьте:
Как быстро и просто считать проценты в уме
В Интернете за каждой социальной сетью закрепилась определённая репутация, и так за Twitter — забавные истории и неожиданный лайфхаки. Уже никто не вспомнит, кто первым заговорил о том, как научиться считать проценты от числа и от суммы в уме, но способ оказался действительно простым и, что важнее, полезным для любого человека.
Британский копирайтер Бен Стивенс (Ben Stephens) назвал эту хитрость «маленьким лайфхаком». Суть его заключается в простой перестановке чисел, которая и помогает добиться искомого результата. Сама по себе методика не нова, однако колоссальная ответная реакция со стороны пользователей Сети доказывает, что многим она была незнакома.
Так как же научиться быстро считать проценты в уме:
Первое, что нужно сделать – перевернуть цифры.
«Допустим, вам надо извлечь 4% от 75 в голове, причем быстро. Как это сделать? Просто найдите 75% от 4, это намного проще». И в самом деле, 75% (то есть три четверти) от числа 4 равняются 3! Переворачиваем цифры обратно, проверяем. Снова 3! Работает!
Другой пример: найти 18% от 50. Звучит довольно сложно, но. Снова меняем цифры местами – и теперь нам надо найти 50% (т.е. половину) от числа 18. С этой задачей справится и ребенок.
Общую формулу Стивенс записывает так:
Буквально за несколько дней математический твит собрал свыше 5 тысяч репостов и 14 тысяч лайков. Оказалось, многие школьные преподаватели не рассказывали ученикам о таком фокусе. Даже сложно представить, как бы упростилась жизнь школьников и студентов, если бы они знали об этой формуле раньше. Но благо, этот способ, как быстро посчитать проценты, хранится в открытом доступе, а потому облегчит жизнь очень многим.
Как быстро считать проценты в уме: математическая хитрость.
Британский копирайтер Бен Стивенс (Ben Stephens) назвал эту хитрость «маленьким лайфхаком». Суть его заключается в простой перестановке чисел, которая и помогает добиться искомого результата. Сама по себе методика не нова, однако колоссальная ответная реакция со стороны пользователей Сети доказывает, что многим она была незнакома. Итак, первое, что нужно сделать — перевернуть цифры:
«Допустим, вам надо извлечь 4% от 75 в голове, причем быстро. Как это сделать? Просто найдите 75% от 4, это намного проще». И в самом деле, 75% (то есть три четверти) от числа 4 равняются 3! Переворачиваем цифры обратно, проверяем… Снова 3! Работает!
Другой пример: найти 18% от 50. Звучит довольно сложно, но… Снова меняем цифры местами — и теперь нам надо найти 50% (т.е. половину) от числа 18. С этой задачей справится и ребенок.
Общую формулу Стивенс записывает так:
Баяны
181K поста 12K подписчиков
Правила сообщества
Сообщество для постов, которые ранее были на Пикабу.
Автор, найди ка в своем умишке 21% от 179.
Вчера же уже повозили мордой по говну этого Бена.
Математик решил загадку числа 42
В течение 65 лет математики по всему миру пытались решить своеобразную головоломку и найти три числа, сумма кубов которых составила бы 42. И, кажется, им наконец удалось.
Задача звучит следующим образом: может ли любое число от 1 до 100 быть выражено как сумма трех кубов?
Если записать формулу 1954 года, то получится следующее: х^3 + y^3 + z^3 = K.
K в данном случае — любое число от 1 до 100. Соответственно, нужно было определить все три неизвестные переменные для каждого числа K в этом промежутке.
В последующие десятилетия были найдены решения для простых чисел. В 2000 году математик Ноам Элкис из Гарвардского университета опубликовал алгоритм, который помог найти более сложные. К 2019 году нерешенными остались только два самых сложных числа: 33 и 42.
Как и многие современные открытия, разгадке поспособствовал Youtube. Математик Эндрю Букер с канала Numberphile опубликовал решение задачи для числа 33, написав собственный алгоритм. Для этого ему понадобился мощный суперкомпьютер в Университете Advanced Computing Research Center, а решение удалось получить всего за три недели.
Итак, у нас осталось самое сложное число: 42. Для его решения Букер заручился поддержкой математика MIT Эндрю Сазерленда, эксперта в области массовых параллельных вычислений. В свою очередь, они прибегли к помощи Charity Engine — инициативы, которая охватывает весь земной шар, используя остаточную вычислительную мощность более 500 000 домашних ПК, в результате получая своего рода «планетарный суперкомпьютер».
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
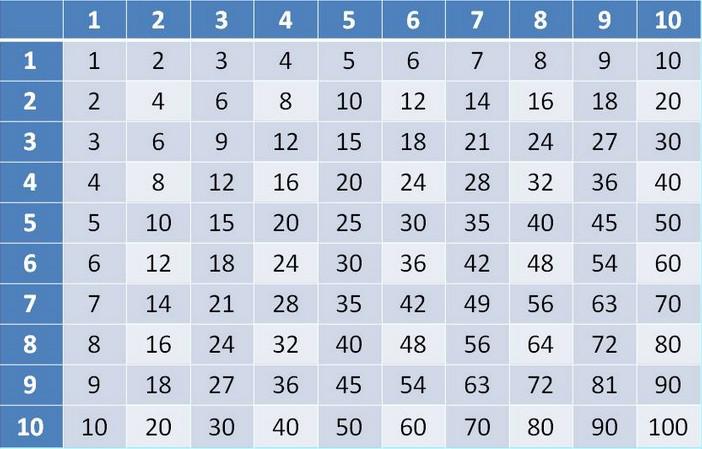
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Что такое ментальная арифметика и как ей научиться
Об эксперте: Анастасия Кузнецова, методист онлайн-школы «Фоксфорд», автор и преподаватель курсов повышения квалификации по ментальной арифметике.
Что такое ментальная арифметика
Попробуйте за несколько секунд решить пример без черновика и калькулятора:
Дети решают такие задачи в уме с помощью ментальной арифметики. Это система развития интеллекта, построенная на обучении устному счету.
Современные родители часто рассказывают о неразвитом воображении и фантазии у ребенка. Дело в том, что мы тренируем левое полушарие мозга ребенка — оно отвечает за логику и математические способности, — но очень мало развиваем правое. Правое полушарие мозга распознает сложные визуальные и звуковые образы. Отвечает за концентрацию внимания и воображение. От гармоничного развития двух полушарий мозга ребенка зависят его когнитивные способности [1].
Ментальная арифметика — это способ развития детского интеллекта с помощью быстрого счета в уме. Сначала ребенок учится считать на счетах-абакус и тренирует мелкую моторику рук. Затем счеты убирают, ребенок представляет их в голове — считает ментально. Развивает воображение и креативность.
Ментальная арифметика помогает комплексно развивать интеллектуальные способности. Моментальный устный счет — приятное дополнение.
Овладев ментальной арифметикой, ребенок намного легче справляется с любой интеллектуальной и творческой работой. Он умеет быстро решать задачи и применять к ним нестандартный подход.
История возникновения ментальной арифметики
Ментальную арифметику придумали около 5 тыс. лет назад. Методикой пользовались в Древней Греции, Индии и Риме, чтобы научить детей считать. В ее основе — умение вычислять на древних счетах-абакус.
Со временем счеты доработали до калькулятора, в 1993 году сформулировали понятие «ментальной арифметики». Сегодня ментальную арифметику используют в 50 странах мира. В Японии и Китае она стала частью школьной программы.
Польза ментальной арифметики
Умение быстро вычислять в уме — не конечная цель. В момент отказа от работы с реальными счетами-абакус правое полушарие мозга начинает работать активнее. В это же время дети развивают логическое мышление и счет, за которые отвечает левое полушарие.
Усиленная работа обоих полушарий мозга становится привычкой и помогает ребенку креативнее решать жизненные задачи. Концентрироваться, смотреть на проблему шире и строить логические цепочки для ее решения. Еще один плюс — развитие сразу нескольких видов памяти: долговременной, кратковременной и фотографической.
Что ученые думают о ментальной арифметике
Американские исследователи проверяли влияние ментальной арифметики на интеллектуальные способности учеников первых и вторых классов в течение года [2]. Результаты получились неоднозначными — первоклассники не справлялись с устным счетом, ребята из второго класса учились лучше, но ученые не выявили заметного улучшения когнитивных способностей.
В 2016 году психолог Дэвид Барнер группой ученых провел подобное исследование в Индии, но за детьми наблюдали уже в течение трех лет [3]. Ментальная арифметика помогла некоторым школьникам лучше учиться, но результат может зависеть и от способностей конкретного ученика. В большинстве других исследований тоже проверяли навыки арифметики. Достаточного количества данных о том, как ментальная арифметика влияет на когнитивные способности, пока нет, поэтому выводы делать рано.
Когда и где учиться ментальной арифметике
Самый подходящий возраст для обучения — от 4 до 12-14 лет. В это время мозг развивается интенсивнее, чем в другие периоды взросления. После 12-14 лет способность мозга приобретать и использовать сложные навыки в таком количестве и темпе снижается.
Сейчас набирают популярность занятия ментальной арифметикой с пожилыми людьми. Такая тренировка мозга — отличный метод профилактики болезней, связанных с памятью и концентрацией внимания.
Самостоятельное обучение может стать непростой задачей. Учеба требует усидчивости, внимательности и разнообразные форматы занятий. Чтобы правильно обучить ребенка ментальной арифметике, лучше обратиться к квалифицированному педагогу.
Как выбрать школу или курс ментальной арифметики
Чтобы выбрать подходящую школу ментальной арифметики для ребенка, проверьте: