неверно что солнце движется вокруг земли информатика
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание
В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.
1) Число 376 чётное и трёхзначное.
2) Зимой дети катаются на коньках или на лыжах.
3) Новый год мы встретим на даче или на Красной площади.
4) Неверно, что Солнце движется: вокруг Земли.
5) Земля имеет форму шара, который из космоса кажется голубым.
6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
Ответ
1) А = Число 376 четное.
В = Число 376 трехзначное.
А ∧ В
2) А = Зимой дети катаются на коньках.
В = Зимой дети катаются на лыжах.
А ∨ В
3) А = Новый год мы встретим на даче.
В = Новый год мы встретим на красной площади.
А ∨ В
4) А = Солнце движется вокруг земли
НЕ А
5) А = Земля имеет форму шара.
В = шар из космоса кажется голубым.
А ∧ В
6) А = На уроке математики старшеклассники отвечали на вопросы учителя.
В = На уроке математики старшеклассники писали самостоятельную работу.
А ∧ В
Задания для самостоятельной работы по теме «Алгебра логики»
Задания для самостоятельного выполнения по теме «Алгебра логики»
1. Выделите в составных высказываниях простые. Обозначьте каждое их них буквой; запишите с помощью логических операций каждое составное высказывание.
1) Число 376 четное и трехзначное.
2) Неверно, что Солнце движется вокруг Земли.
3) Если сумма цифр числа делится на 3, то число делится на 3
4) Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3.
2. Ниже приведена таблица, левая колонка которой содержит основные логические союзы (связки), с помощью которых в естественном языке строятся сложные высказывания. Заполните правую колонку таблицы соответствующими названиями логических операций.
3. Найдите значения логических выражений:
4. Даны два простых высказывания:
Какие из составных высказываний истинны:
а) 

5. Даны простые высказывания:
6.Даны простые высказывания:
Определите истинность составных высказываний:
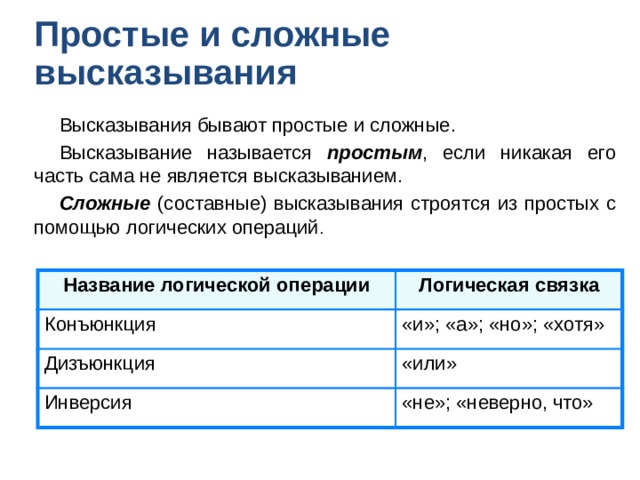
в) (А В) (C D); г) 

7. Дано составное высказывание не (не А и B), где A и B — простые высказывания. В каком случае данное высказывание будет ложным?
8. Выполните поразрядное логическое сложение двоичных чисел:
а) 100 и 110; б) 1010 и 1000; в) 101010 и 111111
Ответы:
2) А = <Солнце движется вокруг Земли>, 
3. а) 1 б) 1 в) 1 г) 0 д) 1 е) 1 ж) 1 з) 0 и) 0
8. а) 110 б) 1010 в) 111111
9. 11011101, 1111101110010, 10101111, 1011100
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Методическая работа в онлайн-образовании
Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-613217
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Только каждый 10-й россиянин может дать платное образование своим детям
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В России утверждены новые аккредитационные показатели для школ и колледжей
Время чтения: 2 минуты
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Минобрнауки обновит перечень специальностей высшего образования
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Таблицы истинности. Решение задач
Содержимое разработки
Задание 2. В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Неверно, что Солнце движется вокруг Земли
А= Солнце движется вокруг Земли
Задание 3. В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Число 376 чётное и трёхзначное.
А= Число 376 чётное ; B= Число 376 трёхзначное
А И В; А & В; А • В; A AND В; A B
А= Новый год мы встретим на даче ;
B= Новый год мы встретим на Красной площади
А ИЛИ В; А OR В; А V В; А | В; A + В
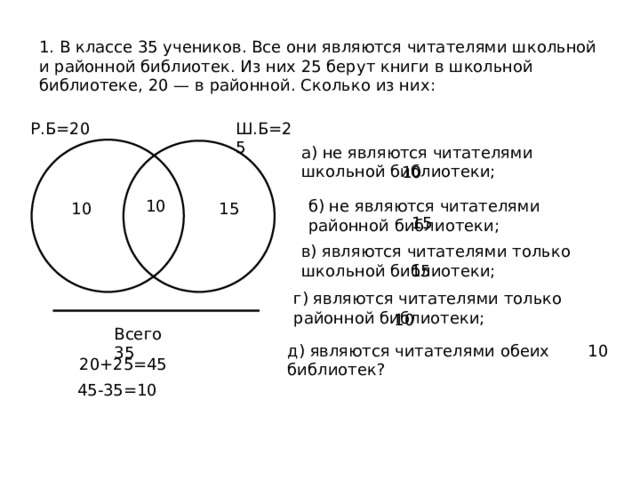
1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них:
а) не являются читателями школьной библиотеки;
б) не являются читателями районной библиотеки;
в) являются читателями только школьной библиотеки;
г) являются читателями только районной библиотеки;
д) являются читателями обеих библиотек?
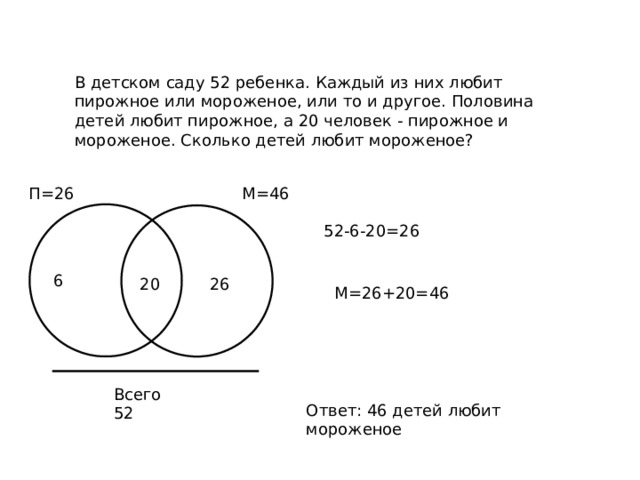
Ответ: 46 детей любит мороженое
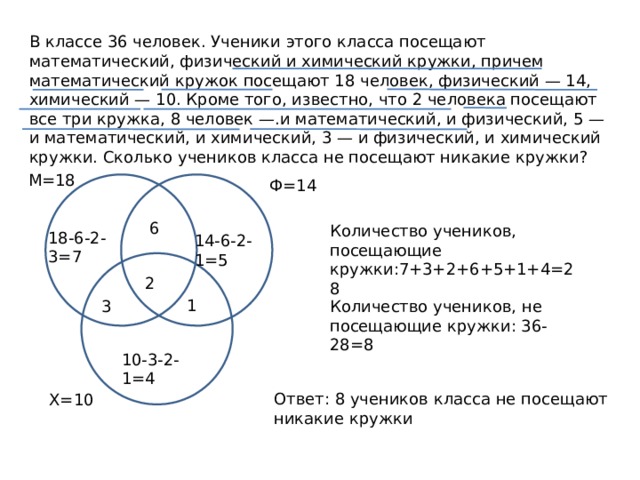
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек —.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?
Количество учеников, посещающие кружки:7+3+2+6+5+1+4=28
Количество учеников, не посещающие кружки: 36-28=8
Ответ: 8 учеников класса не посещают никакие кружки
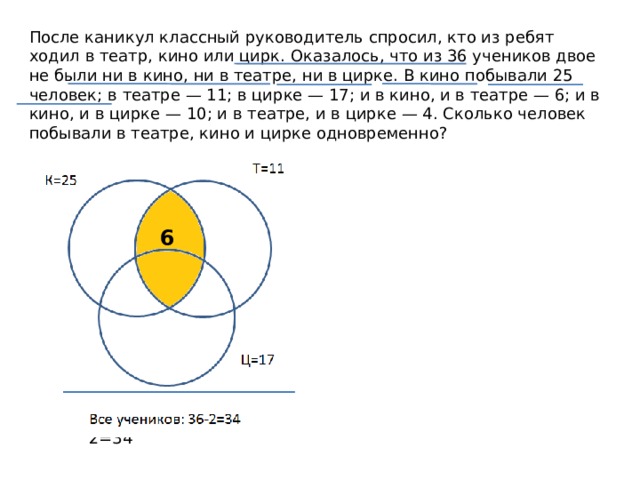
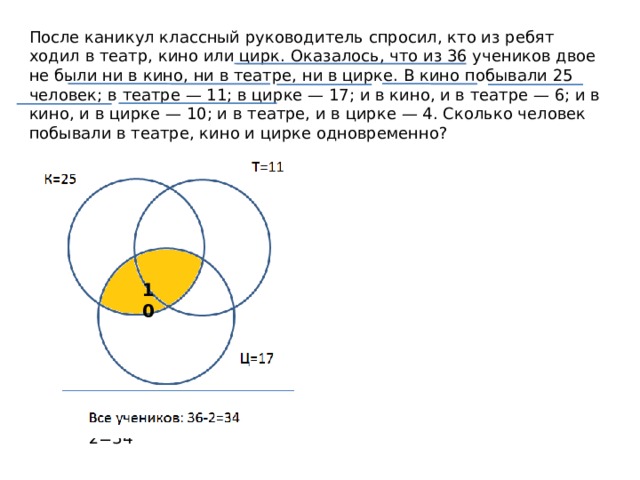
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Все учеников: 36-2=34
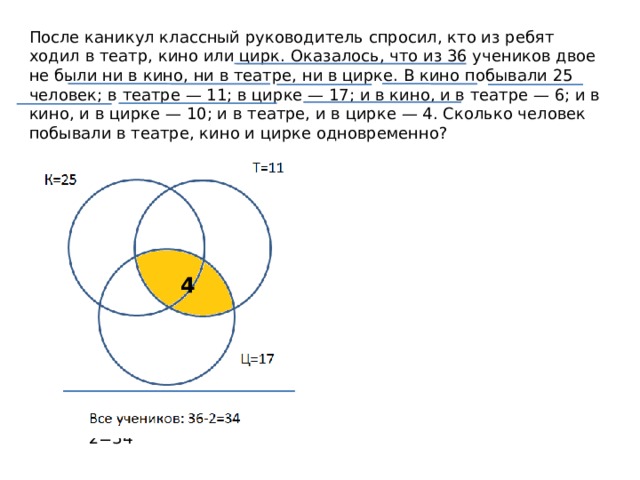
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Все учеников: 36-2=34
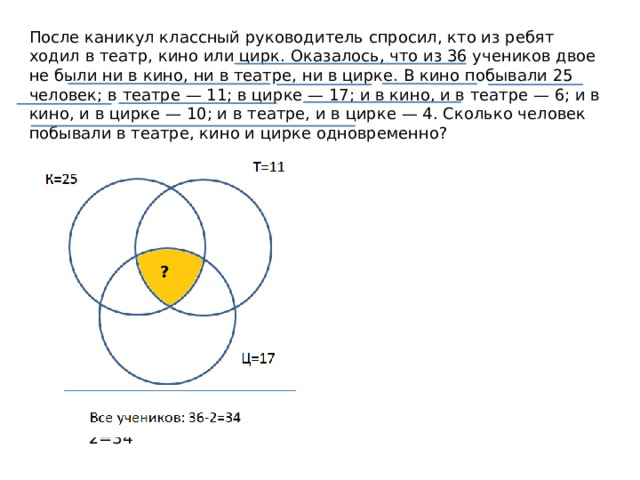
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Все учеников: 36-2=34
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Все учеников: 36-2=34
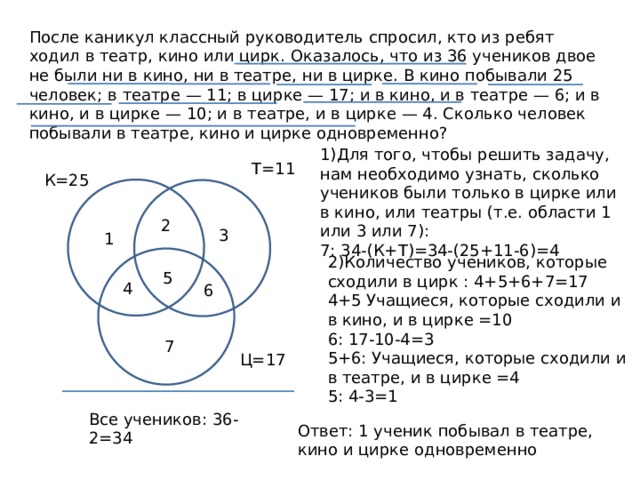
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
1)Для того, чтобы решить задачу, нам необходимо узнать, сколько учеников были только в цирке или в кино, или театры (т.е. области 1 или 3 или 7):
2)Количество учеников, которые сходили в цирк : 4+5+6+7=17
4+5 Учащиеся, которые сходили и в кино, и в цирке =10
5+6: Учащиеся, которые сходили и в театре, и в цирке =4
Все учеников: 36-2=34
Ответ: 1 ученик побывал в театре, кино и цирке одновременно
Простые и сложные высказывания
Высказывания бывают простые и сложные.
Название логической операции
Решение логических выражений принято записывать в виде таблиц истинности .
Таблица истинности – таблица, в которой по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо:
С помощью таблиц истинности можно проверить истинность любых сложных высказываний.
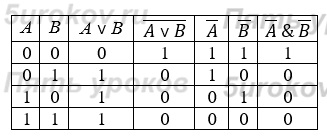
Построим таблицу истинности для выражения:
Количество строк = 2 2 (2 переменных)+ 1()заголовки столбцов=5.
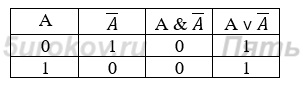
Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (v, &, ¬, v, ¬ )=7
Построим таблицу истинности для выражения:
Построим таблицу истинности для выражения:
Ответы по параграфу 1.4 Элементы алгебры логики
Задание 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
Задание 2. Объясните, почему следующие предложения не являются высказываниями.
Задание 3. Приведите по одному примеру истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.
• География:
1) Столица Италии – Париж. (ЛОЖЬ, т.к. это Рим, а Париж во Франции)
2) Выделяют 4 основные стороны света – север, юг, запад, восток.
• Информатика:
1) Инверсия – это логическое отрицание.
2) Конъюнкция – это логическое сложение. (ЛОЖЬ, т.к. это дизъюнкция является логическим сложением)
• История:
1) Промышленная революция (конец XVIII – первая половина XIX в.) началась в Англии в последней трети XVIII в.
2) Во времена аграрной революции в Англии в конце XVIII века землей владели фермеры, которые сдавали ее в аренду за определенную плату. (ЛОЖЬ, т.к. владели лендлорды, а фермеры были арендаторы)
• Математика:
1) У треугольника 5 сторон.
2) Квадрат гипотенузы равен сумме квадратов двух катетов.
• Литература:
1) Народные частушки – небольшие лирические песни, обычно имеющие форму четырехстрочного рифмованного куплета.
2) Первые упоминания о частушках относятся к 60-м годам XII века. (ЛОЖЬ, т.к это поздний жанр, появившийся только в XIX веке)
Задание 4. В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.
1) Число 376 чётное и трёхзначное.
А = Число 376 чётное
В = Число 376 трёхзначное
A & B
2) Зимой дети катаются на коньках или на лыжах.
A = Зимой дети катаются на коньках
B = Зимой дети катаются на лыжах
A | B
3) Новый год мы встретим на даче или на Красной площади.
A = Новый год мы встретим на даче.
B = Новый год мы встретим на Красной площади.
A | B
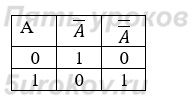
4) Неверно, что Солнце движется вокруг Земли.
A = Солнце движется вокруг Земли
¬A
5) Земля имеет форму шара, который из космоса кажется голубым.
A = Земля имеет форму шара, который из космоса кажется голубым.
B = Шар из космоса кажется голубым.
A & B
6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
A = На уроке математики старшеклассники отвечали на вопросы учителя
B = На уроке математики старшеклассники писали самостоятельную работу
A & B
Задание 5. Постройте отрицания следующих высказываний.
Задание 6. Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:
Задание 7. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
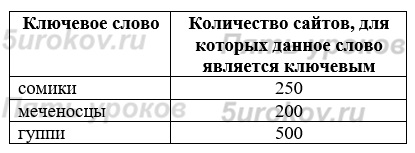
Дано дополнительно помимо таблицы:
сомики & гуппи – 0 сайтов;
сомики & меченосцы – 20 сайтов;
меченосцы & гуппи – 10 сайтов.
Нарисуем круги Эйлера:
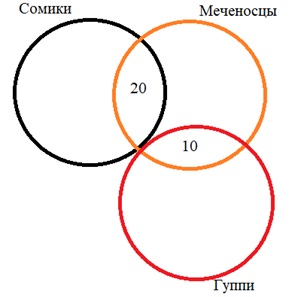
Чтобы найти количество сайтов, соответствующих этому запросу, к количеству элементов множества сомики (250) добавим количество элементов множества меченосцы без сомиков (200 – 20), а также гуппи без меченосцев (500 – 10).
Получаем: 250 + 180 + 490 = 920 сайтов
Ответ: 920 сайтов
2) Найти:
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
То есть это по сути всё, что не вошло в наш С | М | Г, то есть надо найти ¬(С | M | Г).
С | M | Г = 920
По условию задачи сегмент сети Интернет состоит из 1000 сайтов.
То есть, то, что не вошло в нашу область это 1000 – 920 = 80 сайтов.
Ответ: 80 сайтов
Задание 8. Постройте таблицы истинности для следующих логических выражений:
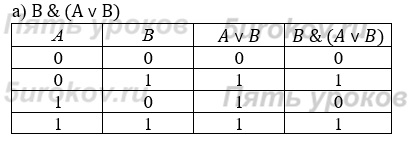
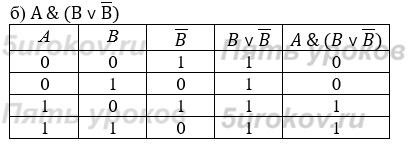
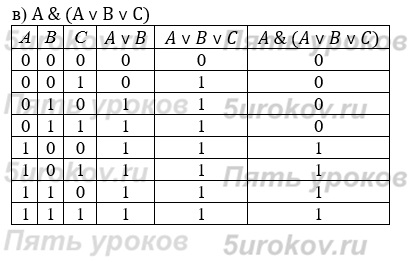
Задание 9. Проведите доказательство рассмотренных в параграфе логических законов с помощью таблиц истинности.
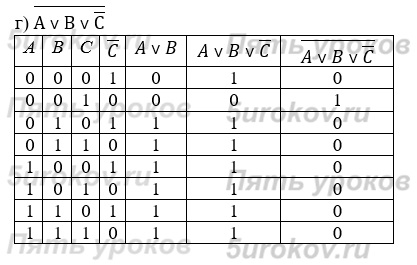
1) Переместительный (коммутативный) закон:
2) Сочетательный (ассоциативный закон):
для логического умножения:
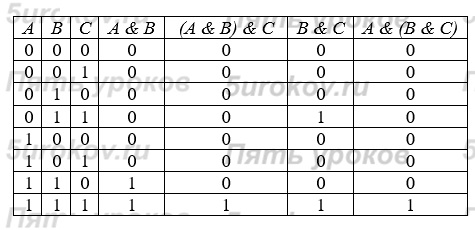
для логического сложения:
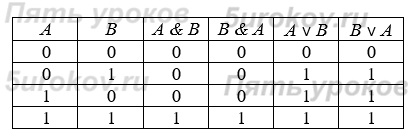
3) Распределительный (дистрибутивный) закон:
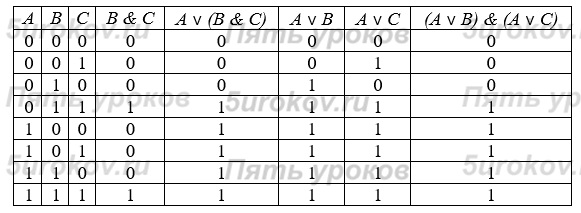
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
4) Закон двойного отрицания:
5) Закон исключенного третьего:
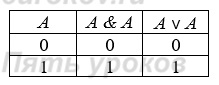
6) Закон повторения:
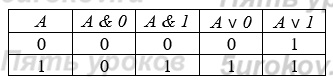
7) Закон операций с 0 и 1:
8) Законы общей инверсии:
а) для логического умножения:
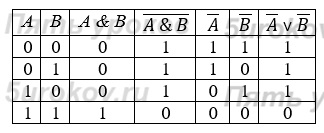
б) для логического сложения:
Задание 10. Даны три числа в десятичной системе счисления: A=23, B=19, C=26. Переведите A, B и C в двоичную систему счисления и выполните поразрядной логические операции (A ˅ B) & C. Ответ дайте в десятичной системе счисления.
Задание 11. Найдите значения выражений:
Задание 12. Найдите значение логического выражения для указанных значений числа Х:
а) 1; б) 2; в) 3; г) 4.
Задание 13. Пусть А = «Первая буква имени – гласная», В = «Четвертая буква имени согласная». Найдите значение логического выражения для следующих имён:
Задание 14. Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это.»
Джон: «Браун не виновен. Смит сделал это.»
Браун: «Я не делал этого. Джон не делал этого.»
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
Задание 15. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения. Где и в каком веке изготовлен сосуд?
Только в 1 прав, в другом не прав, следовательно, иcходя из 2 логических принципов составляем уравнение:
• 0 v 1 = 1
• 1 & 1=1
Усл. Обозначения:
Г – греческий, Ф – Финикийский, Цифра – век
(Г или 5)&(Ф или 3)&(неГ или 4)=1
Распределительный закон, раскрываем скобки:
(ГФ или Г3 или Ф5 или 53) & (неГ или 4)=1
ГФ и 53 обнуляем, т.к. это ложь (0), не может быть одновременно и то, и другое правдой. С тем, что осталось еще раз распределительный закон, раскрываем скобки:
(Г3 и неГ) или Г34 или (Ф5 и неГ) или Ф54 = 1
Г и неГ не может быть одновременно, обнуляем
Г34 обнуляем, Ф54 обнуляем.
Остается:
Ф5 и неГ = 1
Ответ: Финикийский сосуд, изготовлен в V веке.
В таблице приведены запросы к поисковому серверу?
В таблице приведены запросы к поисковому серверу.
Для каждого запроса указан его код – соответствующая буква от А до Г.
Расположите коды запросов слева направо в порядке количества страниц, которые нашёл поисковый сервер по каждому запросу.
По всем запросам было найдено разное количество страниц.
Для обозначения логической операции «ИЛИ» в запросе используется символ «|», а для логической операции «И» – «& ; ».
Код Запрос А Солнце | Воздух | Вода Б Солнце & ; Воздух & ; Вода В (Солнце | Воздух) & ; Вода Г Солнце | Воздух.
Составить составное высказывание, содержащее операции логического умножения, сложения и отрицания?
Составить составное высказывание, содержащее операции логического умножения, сложения и отрицания.
Определить его истинность.
1. Запишите следующее высказывание в виде логического выражения, определив простое высказывание и используя логические операции : А) Если число делится на 4, оно делиться на 2?
1. Запишите следующее высказывание в виде логического выражения, определив простое высказывание и используя логические операции : А) Если число делится на 4, оно делиться на 2.
Тема : Логические операции 8 класс?
Тема : Логические операции 8 класс.
Задание : Сколько логических значений может иметь сложное высказывание, состоящее из : а) двух простых высказываний.
Б) трех простых выказываний.
В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой ; запишите с помощью букв и знаков логических операций каждое составное высказывание : а)на уроке математики уче?
В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой ; запишите с помощью букв и знаков логических операций каждое составное высказывание : а)на уроке математики ученики отвечали на вопросы учителя, а также писали самостоятельную работу.
Б)Две прямые на плоскости параллельны или пересекаются.
С)Неверно, что Солнце движется вокруг Сатурна.
Выделите в составных высказываниях простые?
Выделите в составных высказываниях простые.
Обозначьте каждое из них буквой и запишите с помощью логических операций каждое составное высказывание 1.
Число 456 четное и трехзначное.
2. Неверно, что Солнце движется вокруг Земли.
4. Если на Новый год будет много снега, то мы пойдем на лыжах в лес или уедем кататься в горы.
Определите значения истинности высказываний А, В, С, D если А & ; (Марс – планета) – истинное высказывание ; В & ; (Марс – планета) – ложное высказывание ; С или ( Солнце – спутник Земли) – исти?
Определите значения истинности высказываний А, В, С, D если А & ; (Марс – планета) – истинное высказывание ; В & ; (Марс – планета) – ложное высказывание ; С или ( Солнце – спутник Земли) – истинное высказывание ; D или ( Солнце – спутник Земли) – ложное высказывание.
1. Дано составное высказывание не (не А и B), где A и B — простые высказывания?
1. Дано составное высказывание не (не А и B), где A и B — простые высказывания.
В каком случае данное высказывание будет ложным?
2. Выделите в составных высказываний простое.
Обозначьте каждое их них буквой и запишите с помощью логических операций каждое составное высказывание : Число 376 трехзначное и четное.
Если сумма цифр числа делится на 3, то число делится на 3.
Помогите и объясните, пожалуйста?
Помогите и объясните, пожалуйста.
Среди следующих высказываний укажите составные ; выделите в них простые, обозначив каждое из них буквой ; запишите с помощью логических операций каждое составное высказывание : 1) Число 376 четное и трехзначное.
2) Неверно, что Солнце движется вокруг Земли.
3) Земля имеет форму шара.
4) На уроке математики старшеклассники отвечали на вопросы учителя и писали самостоятельную работу.
5) Если сумма цифр числа делится на 3, то число делится на 3.
6) Число делится на 3 тогда и только тогда, когда сумма цифр числа делится на 3.