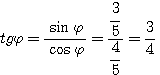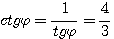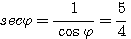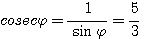найдите значения тригонометрических функций угла если известно что

Найдите значения тригонометрических функций угла если известно что

Найдите если и

Поскольку угол лежит в четвёртой четверти, его тангенс отрицателен. Поэтому

тангенс в третьей четверти ведь положительный, получается, в ответе ошибка

Угол принадлежит 4 четверти.

Куда пропала цифра один в числителе?

Найдите если и

Поскольку угол альфа лежит в третьей четверти, его тангенс положителен. Поэтому

Разве тангенс от 90′ до 135′ не отрицателен?

В третьей четверти тангенс неотрицателен.

Найдите если и

Поскольку угол α лежит в четвертой четверти, его косинус положителен. Поэтому

В задании дан минус около 2 корня из 2/3. А если ориентироваться на ваш ответ, то минуса не должно быть! Здесь явная опечатка.

,

.

Найдите если и

Поскольку угол альфа лежит в четвертой четверти, его синус отрицателен. Тогда

Из основного тригонометрического тождества получается

Но, так как речь идет о промежутке, на котором синус отрицателен (четвертая четверт), то из двух возможных значений выбираем отрицательное

Найдите если

Используем формулу косинуса двойного угла Имеем:

Источник

Найдите значения тригонометрических функций угла если известно что

Нахождение значений тригонометрических функций угла по значению какой-нибудь одной из них.

Используя основные тригонометрические тождества, легко найти значения всех тригонометрических функций sin х, cos х, tg x, ctg x, sec x, cosec x, если известно значение какой-нибудь одной из них. Поясним это на конкретных примерах.

Пример 1. Найти значения тригонометрических функций угла φ, если известно, что sin φ = 3 /₅.

Из тождества sin 2 φ + cos 2 φ = 1 находим: cos 2 φ = 1 — sin 2 φ = 16 /₂₅

Знак + или — следует выбирать в зависимости от того, в какой четверти оканчивается угол φ.

Значит, угол φ оканчивается либо в 1-й, либо во 2-й четверти.
1)Если он оканчивается в 1-й четверти, то cos φ = + 4 /₅.
2)Если же он оканчивается во 2-й четверти, то cos φ = — 4 /₅.

Пример 2. Найти значения тригонометрических функций угла φ, если известно, что он оканчивается в 4-й четверти и tg φ = — 3 /₄

Используя тождество 1 + tg 2 φ = sec 2 φ, найдем sec φ:

Теперь, используя тождество sin 2 φ + cos 2 φ = 1, найдем sin φ:

Итак, мы получили cos φ, sin φ, tg φ, sec φ. После этого легко найти значения и других тригонометрических функций угла φ:

1. Найти значения тригонометрических функций угла α по следующим данным;

3. Найти значения тригонометрических функций угла φ, если известно, что tg φ = а 2 — 1 ( |а| <1), и угол φ оканчивается не во 2-й четверти.

Источник