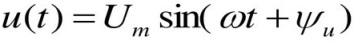Что такое фаза, фазовый угол и сдвиг фаз

Говоря о переменном токе, часто оперируют такими терминами как «фаза», «фазовый угол», «сдвиг фаз». Обычно это касается синусоидального переменного или пульсирующего тока (полученного путем выпрямления синусоидального тока).

Аргументом функции в данном случае является как раз фаза, то есть положение колеблющейся величины (тока или напряжения) в каждый рассматриваемый момент времени относительно момента начала колебаний. А сама функция принимает значение колеблющейся величины, в этот же момент времени.

В процессе изменения, напряжение принимает множество значений в каждый момент времени, периодически (спустя период времени Т) возвращаясь к тому значению, с которого начиналось наблюдение за данным напряжением.

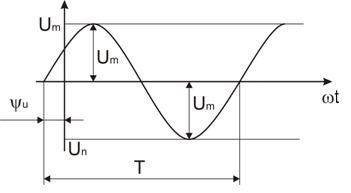
Можно сказать, что в любой момент времени напряжение находится в определенной фазе, которая зависит от нескольких факторов: от времени t, прошедшего от начала колебаний, от угловой частоты, и от начальной фазы. То что стоит в скобках — полная фаза колебаний в текущий момент времени t. Пси — начальная фаза.

Начальную фазу называют в электротехнике еще начальным фазовым углом, поскольку фаза измеряется в радианах или в градусах, как и все обычные геометрические углы. Пределы изменения фазы лежат в интервале от 0 до 360 градусов или от 0 до 2*пи радиан.

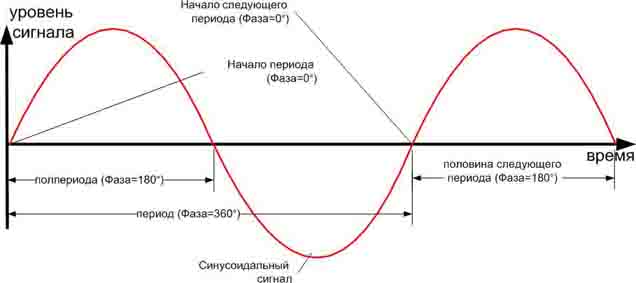
На приведенном выше рисунке видно, что в момент начала наблюдения за переменным напряжением U, его значение не было нулем, то есть фаза уже успела в данном примере отклониться от нуля на некоторый угол Пси, равный около 30 градусов или пи/6 радиан — это и есть начальный фазовый угол.

В составе аргумента синусоидальной функции, Пси является константной, поскольку данный угол определяется в начале наблюдения за изменяющимся напряжением, и потом уже в принципе не изменяется. Однако его наличие определяет общий сдвиг синусоидальной кривой относительно начала координат.

По ходу дальнейшего колебания напряжения, текущий фазовый угол изменяется, вместе с ним изменяется и напряжение.

Для синусоидальной функции, если полный фазовый угол (полная фаза с учетом начальной фазы) равен нулю, 180 градусам (пи радиан) или 360 градусам (2*пи радиан), то напряжение принимает нулевое значение, а если фазовый угол принимает значение 90 градусов (пи/2 радиан) или 270 градусов (3*пи/2 радиан) то в такие моменты напряжение максимально отклонено от нуля.

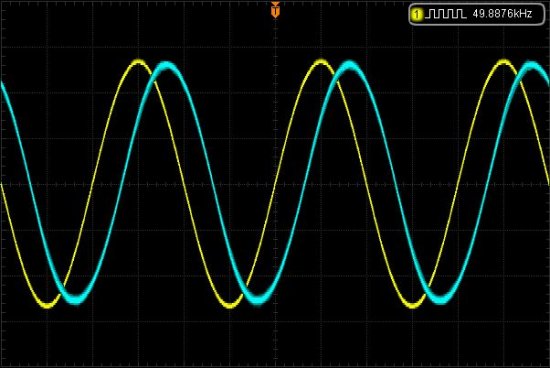
Обычно в ходе электротехнических измерений в цепях переменного синусоидального тока (напряжения), наблюдение ведут одновременно и за током и за напряжением в исследуемой цепи. Тогда графики тока и напряжения изображают на общей координатной плоскости.

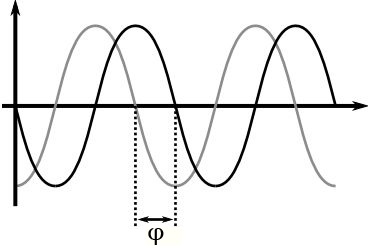
В этом случае частота изменения тока и напряжения идентичны, но различны, если смотреть на графики, их начальные фазы. В этом случае говорят о фазовом сдвиге между током и напряжением, то есть о разности их начальных фазовых углов.

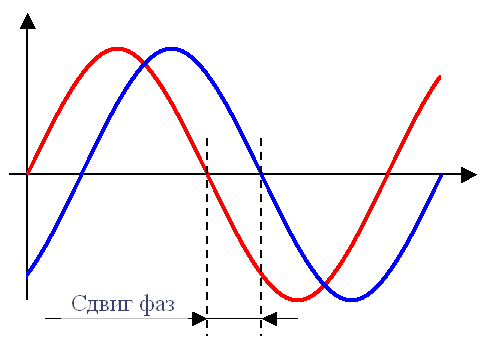
Иными словами фазовый сдвиг определяет то, на сколько одна синусоида смещена во времени относительно другой. Фазовый сдвиг, как и фазовый угол, измеряется в градусах или радианах. По фазе опережает тот синус, период которого начинается раньше, а отстает по фазе тот, чей период начинается позже. Фазовый сдвиг обозначают обычно буквой Фи.

Фазовый сдвиг, например, между напряжениями на проводах трехфазной сети переменного тока относительно друг друга является константой и равен 120 градусов или 2*пи/3 радиан.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Фаза, противофаза и фазовый сдвиг

В этой статье рассмотрим такой важный вопрос, как фаза аудиосигнала.

При упоминании раздела школьной физики о гармонических колебаниях первое, что приходит на ум, — это то, что фаза представляет собой аргумент периодической функции, определяющий амплитуду сигнала в определенный момент времени.

Что нам от этого в музыкальном плане? И где же могут возникнуть проблемы с этой самой фазой?

Представьте, что мы записываем гитару. Звук снимается с комбоусилителя с помощью двух микрофонов. Сигнал из них микшируется, а затем идет в один канал. Как раз суммирование двух сигналов и может привести к возникновению проблем с фазой.

Сигналы в фазе

Наблюдается идеальное повторение сигналов, при котором «пики и впадины» их амплитуд абсолютно синхронны во времени. В таком случае говорят, что сигналы «в фазе». На практике это означает, что будет иметь место усиление сигналами друг друга. И в идеале амплитуда результирующего сигнала будет равна сумме амплитуд каждого сигнала.

Такой расклад не только ничем нам не грозит, а даже наоборот является весьма желанным и полезным в большинстве случаев.

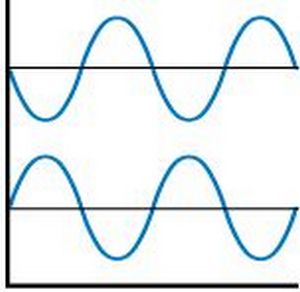
Сигналы в противофазе

На осциллографе заметно, что «пик» первого сигнала совпадает с «впадиной» второго. Из этого несложно сделать вывод, что в результате сложения таких колебаний в идеале получится абсолютный ноль или, иными словами, взаимное подавление обоих сигналов.

Такой расклад ничего хорошего не принесет, поэтому его стоит всячески избегать.

Фазовый сдвиг

Фазовый сдвиг подразумевает запаздывание первого сигнала по времени относительно второго.

При двух гармонических колебаниях одной частоты результатом сдвига фаз будет частичное ослабление сигнала. Степень ослабления результирующего сигнала будет зависеть как раз от этого самого сдвига фаз. В предельном случае на выходе получится абсолютный ноль.

Все эти иллюстрации только отдаленно относятся к практическим реалиям. Звук музыкального инструмента — это ведь отнюдь не одночастотный сигнал. Звук гитары или какого-либо другого инструмента характеризуется довольно большим количеством обертонов.

Поэтому частичный сдвиг фаз может приводить к большему ослаблению одних частот по сравнению с другими, и даже к усилению некоторых из них. Можно легко догадаться, что на все это влияет сдвиг фаз между конкретными гармониками.

К слову сказать, как раз этот принцип усиления одних частот и ослабления других лежит в основе всем известного эффекта – фейзера. Схема включает в себя частотные фильтры, цепи обратной связи и смешивание обработанного и не обработанного сигнала, однако главный принцип заключается именно в сдвиге фаз.

В целом, фазовый фактор может стать причиной многих неприятностей. Хорошо, если при записи используются всего два микрофона. В таком случае можно поэкспериментировать с расстоянием от источника звука до микрофонов, чтобы подобрать такие положения, при которых сигналы от них поступают в фазе. А вот ситуация с использованием например десяти микрофонов уже намного сложнее.

Кстати, многие предусилители для микрофонов оснащены переключателем полярности сигналов. Единственное, что совпадение или несовпадение «пиков» и «впадин» обоих сигналов будет определяться не разностью их фаз, а полярностью. Но поскольку эффект такой же, то для решения проблем с фазой можно применять инвертирование сигналов, которое может принести желаемый результат, и может и нет.

Решить проблему можно и с помощью коррекции фазы уже записанного сигнала в любой программе для звукозаписи, тем более что современная цифровая обработка звука обеспечивает безграничные возможности в этом вопросе.

Заметить фазовое несовпадение сигналов на слух можно по характерной потере яркости звука, его «обеднению». Если вы услышали какие-то разлады со звуком, которые идентичны вышеперечисленным, поэкспериментируйте с фазой.

Фазовые проблемы могут иметь место не только во время снятия звука микрофонами. Например, они могут возникать при включении фейзера в параллельный разрыв на комбике, так как фэйзер сам по себе приводит к сдвижению фазы исходного сигнала и ее дальнейшему смешиванию с необработанным сигналом. К тому же не стоит забывать и о параллельной петле. В результате — прогнозируемое плохое звучание.

Источник

Сдвиг фаз переменного тока и напряжения

Мощность постоянного тока, как мы уже знаем, равна про­изведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При пере­менном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденса­торов и катушек индуктивности.

Для этого случая формула мощности

На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.

Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.

При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.

О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.

Представим себе, что при начале вращения радиусы-век­торы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.

Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.

Рассмот­рим, как будут изменяйся при этом ток и напряжение. Из по­строенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.

Затем напряжение достигает своей наибольшей ве­личины и начинает уже убывать, а ток хотя и становится по­ложительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направле­ние, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряже­ния. Между фазами напряжения и тока существует постоян­ный сдвиг, называемый сдвигом фаз.

Действительно, если мы посмотрим на рисунок 2, то заме­тим, что синусоида тока сдвинута вправо относительно сину­соиды напряжения. Так как по горизонтальной оси мы откла­дываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.

Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с на­правлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величи­ны на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источни­ком ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.

Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрица­тельной, тем, следовательно, меньше будет средняя мощность тока.

При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).

Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.

Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы

в этом случае будут неверны

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Фазовый сдвиг. Фаза сигнала. 1 min read

Фазовый сдвиг – что это? А фаза звукового сигнала? Попробуем немного разобраться в этом вопросе. Не факт, что смогу ясно разъяснить этот вопрос, но примерное понятие должно получиться.

Пролог

Музыканты, меломаны, а так же, любители “хай-эндовского” звука, в разговорах между собой, часто используют, вроде бы всем понятные термины – спектр, фаза, частота, меандр, глубина и локализация сцены, и прочие узкозначимые слова. Но зачастую, даже некоторые из “знатоков”, до конца не могут понять, что же это на самом деле такое.

Такие понятия как – “Фазовый сдвиг” очень часто упоминаются при проектировании кроссоверов для акустики. Подробно про кроссоверы мы уже поговорили чуть ранее.

При наличии интернета выяснить тот или иной вопрос не составляет проблем. В отсутствии такового – можно сходить в библиотеку, найти пару реально научных книжек и почитать саму теорию. Но все нынче стали на столько занятые, что даже выуживать информацию из интернета – времени нет. Попробуем найти простое объяснение – что же такое “фазовый сдвиг”?

Что означают эти термины на самом деле? Можно ли “пощупать” их истинное значение? Да, однозначно, можно. Сейчас мы попробуем разобраться в вопросе – “Что такое – фазовый сдвиг?”

Фаза сигнала

Для начала порассуждаем, что такое – “фаза сигнала”. Фаза сигнала никогда не существует сама по себе. Это виртуальное понятие. Вообще, можно сказать так: Фаза – это уровень сигнала в текущий момент времени, или иначе, – это уровень звукового давления в текущий момент времени в измеряемой точке пространства (к примеру, это место, где находится слушатель).

Вот картинка, изображающая звуковые волны в фазе. К примеру, звуковые сигналы двух каналов нашей акустики совпадают. В этом случае, музыка звучит чётко, без каких либо искажений. В музыкальном произведении можно услышать все задействованные инструменты, которые звукорежиссер слышал при записи. Имеется некая область звукового давления, где ощущается “эффект присутствия” – это то, о чем спорят меломаны и аудиофилы. Иными словами – получаем ожидаемый звук и впечатления.

На следующей картинке ниже, фаза смещена на 90 градусов, или на четверть фазы. Этот эффект можно услышать в виде небольшого эха. Это может и не связано с оборудованием самой комнаты. Эффект звуковой задержки с небольшим смещением фазы вносит некую сумятицу в музыку, теряется “картинка”, исполнители “уходят в разные стороны”, появляется ощущение, что находишься в огромном зале с каменными стенами. Звуки становятся не естественными, искаженными.

Далее, мы наблюдаем смещение фаз на 180 градусов. То есть, акустика в этом случае играет в противофазе. Чуть ниже подробно об этом. В данном случае, общая “звуковая картина” на столько становится не понятной, что слушать музыку становится просто не интересно и противно. Звуки становятся “ватные”, многие часты просто могут отсутствовать, хотя они и воспроизводятся колонками. Может сложиться такое впечатление, что слушаешь музыку в завязанной шапке-ушанке.

Далее, немного теории без научных выкладок.

К примеру, слушая, сидя у себя дома, свои акустические системы, мы слышим, как они порождают в районе дивана те или иные переменные звуковые давления. Звуковые волны складываются друг с другом. Эти волны имеют разные частоты и амплитуду. Они то нарастают, то убывают.

Противофаза

А теперь предположим, что давления от обоих колонок (звуковые волны) изменяются одинаково, но имеют противоположную направленность. То есть, одна колонка излучает “плюсовые” волны, а другая колонка – “минусовые”. Это может случиться, когда слушатель, случайно, перепутал клеммы подключения одного из каналов (левый канал например).

Немного проще. Динамики правой колонки играют вперёд, а динамики в левой колонке играют назад, одновременно пытаясь воспроизводить одну и туже частоту. Одна колонка создаёт давление, скажем, 1 Паскаль, а другая – минус 1 Паскаль. Такой эффект называется – противофаза.

Общая громкость звука в том месте, где находится слушатель, теоретически, должна стремится к нулю, но это не означает, что какой либо звук вообще будет не слышно. В этом случае, может сильно поломаться “звуковая сцена”, “картинка” музыкального произведения, а в каком либо месте помещения звук реально будет затухать, но не совсем. Звук станет “смазанным” и исчезнут некоторые частотные составляющие из общего звукового сигнала.

Не будем вдаваться в непростую научную формулировку, приводя формулы. Можно сказать так, что из второй колонки звук доходит к слушателю, но с задержкой по времени (не забываем, что сигнал на колонки подаётся одинаковый!). И задержка в этом случае получается именно 180 градусов. Почему так? Попробуем разобраться на картинке, нагляднее – понятнее.

360 градусов – длина периода сигнала (Фаза), 180 градусов – половина периода сигнала.

Фазовый сдвиг

А теперь, мы дошли до момента, когда можно уже разобрать вопрос – “Что такое – фазовый сдвиг?”

Фаза — это временная связь двух сигналов. И в течении периода колебания меняется от 0 до 360 градусов. Потом опять – от 0 до 360, и так далее. Можно сказать, что это мгновенный уровень сигнала в определенной точке времени внутри периода. Саму фазу мы не слышим, но слышим фазовый сдвиг одного сигнала относительно другого.

Вики про это говорит так: Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.

Фазовый сдвиг является безмерной величиной и измеряется в градусах или долях периода.

Вывод

Предположим, вы подключили два динамика к выходу усилителя (пусть физически это будут ваши акустические системы). Один динамик как положено – плюс на плюс, минус на минус. А второй, перепутали и он получился подключенным плюс на минус и минус на плюс. Включив усилитель, что мы услышим? Вероятнее всего – жалкое подобие звука. Один динамик будет как-бы гасить сигнал другого своими звуковыми волнами.

На картинках ниже будет нагляднее. Представим, что это мы видим на экране осциллографа, который измеряет сигналы левого и правого каналов вашего усилителя.

На первой картинке левый и правый канал – в фазе. Сигнал одинаков в обоих каналах. Линии идеально повторяют сигнал. У них синхронная амплитуда на всем протяжении. Тут можно сказать, что сигналы находятся «в фазе». Если практически, то суммирующий уровень сигнала будет усиливаться сигналами левого и правого каналов.

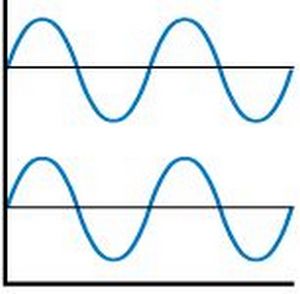
Вторая картинка демонстрирует осциллограмму полного не совпадения. “Горб” левого канала по времени совпадает с “ямой” правого. Чисто по школьной физике – в результате сложения таких колебаний, в идеале, получится ноль. Эти сигналы будут взаимно подавлять друг друга. Сигналы в противофазе.

Фазовый сдвиг подразумевает запаздывание первого сигнала по времени относительно второго.

При двух гармонических колебаниях одной частоты результатом сдвига фаз будет частичное ослабление сигнала. Степень ослабления результирующего сигнала будет зависеть как раз от этого самого сдвига фаз. В предельном случае (в противофазе), на выходе получится абсолютный ноль.

Все эти картинки и рассуждения, о физических свойствах звуковых волн, отдаленно относятся к практике, к реальности. Звуки любого музыкального инструмента нельзя назвать – “одночастотным сигналом” (как осциллограмма на картинках). Частичный сдвиг фаз может ослаблять одни частоты по сравнению с другими. А иногда, усиливать некоторые из них.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

3. Частотные характеристики систем автоматического управления (АФЧХ, ЛАХ, ФЧХ) ч. 3.1

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В этом разделе мы будем изучать частотные характеристики. Тема сегодняшней статьи:
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ

Будет интересно, познавательно и жестко.

3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ, ЛАХ, ФЧХ

Определение: Частотными характеристиками называются формулы и графики, характеризующие реакцию звена (системы) на единичное синусоидальное воздействие в установившемся режиме, т.е. в режиме вынужденных гармонических колебаний звена (системы).

Формула синусоидального воздействия может быть записана как:

— сдвиг фазы (нередко называют — фаза);
— амплитуда;
т.е. амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия x(t).

Используем показательную форму записи функции единичного гармонического воздействия и отклика на это воздействие (рис. 3.1.1):

Определим связь между передаточной функцией и гармоничным воздействием, пользуясь показательной формой.
Рассмотрим звено уравнение динамики которого имеет следующий вид:

В показательной форме:

Запишем в показательной форме используя соотношения 3.1.1:

Подставим эти соотношения в (3.1.1) получим:

Поскольку (амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия), то можно записать:

если вспомнить, что в преобразования Лапласа , то:

Получаем выражение для передаточной функции

— Амплитудно-фазовая частотная характеристика (АФЧХ)
Иногда называют частотной передаточной функцией.
Модуль АФЧХ= тождественно равен амплитуде выходного сигнала:

Сдвиг фазы выходного сигнала:

Обычно АФЧХ изображается на комплексной плоскости. Формулы (3.1.6) и (3.1.7) позволяют изобразить в полярных координатах
Так же можно изображать в традиционных декартовых координатах:

Если использовать для представления W(s) форму W(s)=K·N(s)/L(s), где L(s)- полиномы по степеням s, (причем свободные члены равны 1), а К – общий коэффициент усиления звена (системы), то

Сдвиг фазы можно определить по виду многочленов и (см. формулу (3.1.9)) т.е. как разность фаз (аргументов) числителя и знаменателя:

Постоим АФЧХ для «абстрактного» звена (системы) с передаточной функцией:

Подставляя в формулу различные значения , получаем набор векторов, на комплексной плоскости

Рассмотрим действительную и мнимую части полученных векторов Из рисунка 3.1.3 видно, что:

Амплитуда и сдвиг фазы рассчитываются для векторов, соответствующих положительным частотам и лежащих в 4 квадранте по формулам:

В общем случае для любых углов сдвига необходимо учитывать переход между квадрантами на плоскости. Тогда формула принимает вид:

где:
j = 0, 2, 3, 4. если вектор в I и IV квадрант;
j = 1, 3, 4, 4. если вектор в II и III квадранте.

Во всех технических системах отклик системы, как правило, отстает от входного воздействия, то есть сдвиг фазы всегда отрицательный. Исходя из формулы 3.1.10, степень полинома L(s) выше, чем полинома N(s). Поскольку обычно степень полинома L(s) выше, чем полинома N(s), то с увеличением частоты на входе в звено (в систему) сдвиг фазы обычно отрицателен, т.е. сигнал на выходе звена еще больше отстает по фазе от входного сигнала при увеличении частоты.
В предельном случае, если частота растет до бесконечности, мы можем вообще не получить выходного воздействия. Обычно при ω→ ∞ величина амплитуды на выходе звена стремится к 0, то есть lim A(ω→∞) = 0.

при замене на имеет зеркальное изображение.

Анализируя годографы АФЧХ при > 0 (сплошная линия на рисунке 3.1.3) и при Рисунок 3.1.4 – «Зеркальная» симметрия относительно оси ординат.

Кроме анализа свойств звена (системы) по годографу АФЧХ, широкое распространение получили анализ логарифмической амплитудной характеристики (ЛАХ) и фазочастотной характеристики (ФЧХ).

ЛАХ определяется как Lm(ω)=20lgA(ω).

Поскольку зачастую удобнее использовать десятичные логарифмы (lg), чем натуральные(ln), в теории управления (также и в акустике) значительно чаще используется специальная единица – децибел (1/10 часть Бела):
+1Бел – единица, характеризующая увеличение в 10 раз.
+1дБ (децибел) – соответствует увеличению в раз.

В формуле Lm(ω)=20lgA(ω) величина Lm(ω) измеряется также в децибелах. Происхождение множителя 20 таково: A(ω) – амплитуда, линейная величина, а мощность — квадратичная величина (например, напряжение в сети измеряется в Вольтах, а мощность () пропорциональна квадрату напряжения, поэтому в формуле для Lm(ω) стоит множитель 20 (чтобы привести ЛАХ (Lm(ω)) к традиционной мощностной характеристике).

Если больше на 20 дБ, то это означает, амплитуда больше амплитуды в 10 раз,

Окончательно: Lm(ω)=20lg│W(iω)│= 20lgA(ω)

Графики A(ω) и φ(ω) имеют вид:

Учитывая, что “ω” обычно изменяется на порядки и значение A(ω) – также на порядки, график Lm(ω) строится, фактически, в логарифмических координатах, т.е. Lm(ω) =Lm(lg(ω)), например:

Наклон (– 40 дБ/дек) соответствует уменьшению амплитуды в 100 раз при увеличении частоты в 10 раз.

Рассмотренные характеристики Lm(ω), то есть ЛАХ и ФЧХ имеют широкое распространение при анализе динамических свойств звена (системы), например, при анализе устойчивости САР (см. раздел “Устойчивость систем автоматического управления”).

Рисунок 3.1.10 – пример ЛАХ и ФЧХ для сложной системы

Пример 1

Параметры блока «Построение частотных характеристик» приведены на рисунке 3.1.12, для иллюстрации зависимости АЧХ и ЛАХ. Результат работы блока — график с выбранными параметрами — изображен на рисунке 3.1.13:

Анализ графика в линейном масштабе по ω чаще всего не очень удобен, поскольку весь график собирается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидим практически вертикальные и горизонтальные прямые. Изменения масштаба шкалы АЧХ и ω на логарифмический дает возможность лучше исследовать частотные характеристики (см. рис. 3.1.14).

На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстрация соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.

Пример 2

Постоим частотные характеристики для чуть более сложной модели, а именно — для гидравлического демпфера, рассмотренного в предыдущей лекции.

Для начала посмотрим на модель в виде блоков.

Модель, подготовленная для анализа, представлена на рисунке 3.1.15. В отличие от исходной модели, описанной ранее, входное воздействие задается блоком «ступенька» с скачком с 0 до 1 на 10 секунде расчёта. В блоке «линейная функция» происходит пересчет сигнала «ступенька»:
0 — соответствует 200 бар в камере (конечное состояние в предыдущем примере)
1 — соответствует 400 бар в камере.
Это сделано для того, чтобы можно было подавать синусоидальный сигнал и не получать отрицательное давление в камере плунжера. Также для наглядности графика мы усиливаем выходное перемещение, переводя его из метров в миллиметры.

Частотные характеристики, получаемые в конце расчёта, приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера (сравните с 3.1.14)

Блок «Построение частотных характеристик» осуществляет расчет характеристик для линеаризованной модели в окрестности заданной точки. Это означает, что частотные характеристики системы в разные моменты времени могут отличаться для нелинейных моделей. Например, в нашем случае характеристики в начале расчёта будут отличаться от характеристик, полученных в конце расчёта.

Для подробных и нелинейных моделей, блок «Построение частотных характеристик» может не работать из за наличия разрывов и нелинейностей в модели. Как например, для «точной» модели демпфера, которую мы проверяли в предыдущей статье. В этом случае возможно построить частотные характеристики непосредственно моделированием, путем подачи синусоидального сигнала с разной частотой и измерения отклика. В SimInTech для этого используется блок «Гармонический анализатор», который подключается ко входу модели и генерирует синусоидальное воздействие. В этот же блок направляется отклик системы, и производится вычисление необходимых параметров для построения различных характеристик системы, которые можно вывести на графики с помощью блока «фазовый портрет».

Модель гидравлического демпфера, собранного из библиотечных блоков SimInTech, представлена на рисунке 3.1.7

Расчеты с моделью показывают, что при сохранении общего вида графиков значения, полученные для «подробной модели», отличаются от линеаризованной модели (см. рис. 3.18 — 3.19)

Использование прямого моделирования для получения характеристик является более надежным способом и работает не только с линейными моделями, но также может быть применимо для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно будут больше. Например, для получения характеристик демпфера пришлось выполнить процесс в 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

Блок «Гармонический анализатор» имеет выходы:
Re(w*t) – текущее значение действительной части амплитудно-фазовой частотной характеристики исследуемой системы;
Im(w*t) – текущее значение мнимой части амплитудно-фазовой частотной характеристики.
Это позволяет построить годограф исследуемой системы с помощью фазового портрета. (см. рис. 3.1.21)

Модели, использованные для иллюстрации в лекции можно взять здесь…

Источник