на что влияет эксцентриситет орбиты
Эксцентриситет орбиты
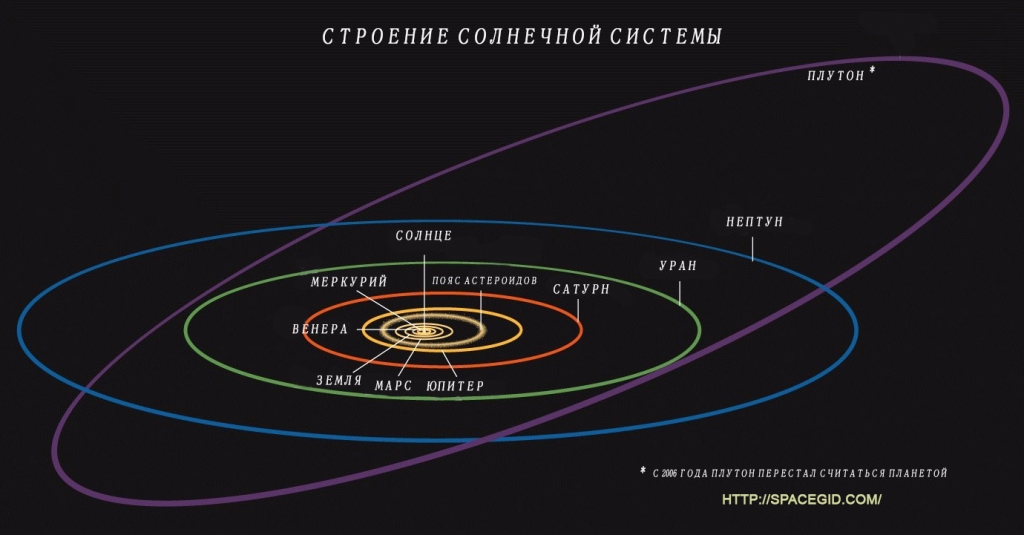
Строение Солнечной системы
Эксцентриситет (обозначается e или ε) входит в шестёрку кеплеровских элементов орбиты. Наряду с большой полуосью он определяют форму орбиты.
Определение эксцентриситета
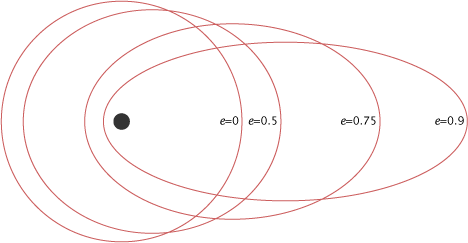
Первый закон Кеплера гласит о том, что орбиты любой планеты Солнечной системы представляет собой эллипс. Эксцентриситет определяет, насколько орбита отлична от окружности. Он равен отношению расстояния от центра эллипса (c) до его фокуса большой полуоси (a).
Эксцентриситеты объектов Солнечной Системы
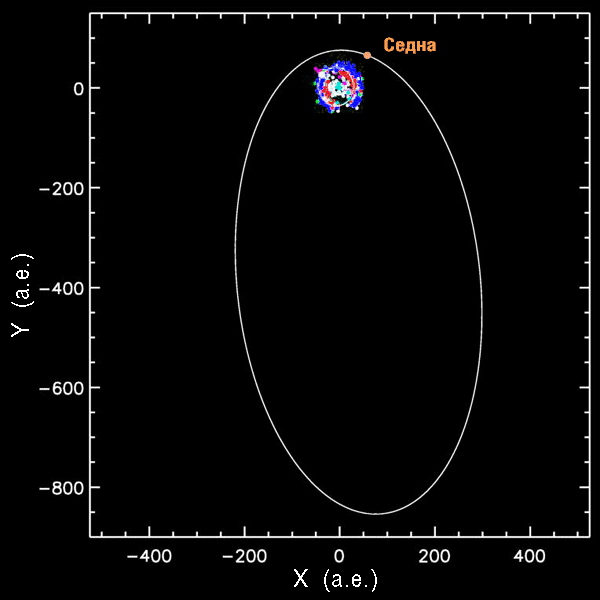
Орбита Седны. В центре координат — Солнечная система, окруженная роем планет и известных объектов пояса Койпера.
В нашей системе орбиты планет ничем не примечательны. Самой «круговой» орбитой обладает Венера. Её афелий всего-лишь на 1,4 млн. км.больше перигелия, а эксцентриситет равен 0,007 (у Земли – 0,016). По довольно вытянутой орбите движется Плутон. Обладая ε = 0,244, он временами приближается к Солнцу даже ближе чем Нептун. Однако, поскольку Плутон не так давно попал в разряд карликовых планет, самую вытянутую орбит среди планет теперь имеет Меркурий, обладающий ε = 0,204.
Среди карликовых планет наиболее примечательна Седна. Обладая ε = 0,86, она делает полный оборот вокруг Солнца почти за 12 тысяч лет, удаляясь от неё в афелии более чем на тысячу астрономический единиц. Однако даже это несравнимо с параметрами орбит долгопериодических комет. Периоды их обращения порой исчисляются миллионами лет, а многих из них и вовсе никогда не вернутся к Солнцу – т.е. обладают эксцентриситетом, большем 1. Облако Оорта может содержать триллионы комет, удалённых от Солнца на 50-100 тысяч астрономических единиц (0,5 – 1 световых лет). На таких расстояниях на нихмогут влиять другие звёзды и галактические приливные силы. Поэтому такие кометы могут обладать очень непредсказуемыми и непостоянными орбитами с самими различными эксцентриситетами.
Наконец, самым интересным является то, что даже Солнце обладает совсем ни круговой орбитой, как это может показаться на первый взгляд. Как известно, Солнце движется вокруг центра Галактики, проделывая свой путь за 223 млн. лет. Причём, из-за бесчисленного взаимодействия со звездами она получила довольно ощутимый эксцентриситет, равный 0,36.
Эксцентриситеты в других системах
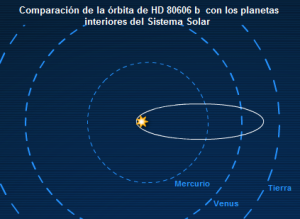
Сравнение орбиты HD 80606 b с внутренними планетами Солнечной системы
Открытие других солнечных систем неизбежно влечёт открытие планет с очень причудливыми параметрами орбит. Примером тому служат эксцентричные юпитеры, газовые гиганты с довольно высокими эксцентриситетами. В системах, имеющие такие планеты невозможно существование планет, подобных Земле. Они неизбежно упадут на гиганты или же статут их спутниками.
Среди обнаруженных на данный момент эксцентричных юпитеров самым большим эксцентриситетом обладает HD 80606b. Он движется вокруг звезды чуть меньшей, чем наше Солнце. Эта планета в перигелии приближается к звезде в 10 раз ближе, чем Меркурий к Солнцу, тогда как в афелии она удаляется от неё почти на астрономическую единицу. Таким образом, она имеет эксцентриситет 0,933.
Стоит отметить, что хоть данная планета и пересекает зону жизни, ни о каких видах привычной биосферы не может идти и речи. Её орбита создаёт на планете экстремальный климат.За короткий период сближения со звездой температура её атмосферы за считанные часы меняется на сотни градусов, в результате чего скорость ветров достигают многих километров в секунду. Подобными условиями обладают прочие планеты с высокими коэффициентами. Тот же Плутон, к примеру, при приближение к Солнцу приобретает обширную атмосферу, которая оседает в виде снега при удалении. В тоже время все Землеподобные планеты обладают орбитами, близкими к круговым. Поэтому эксцентриситет можно назвать одним из параметров, определяющим возможность наличия органической жизни на планете.
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Эксцентриситет орбиты
Строение Солнечной системы
Эксцентриситет (обозначается e или ε) входит в шестёрку кеплеровских элементов орбиты. Наряду с большой полуосью он определяют форму орбиты.
Определение эксцентриситета
Первый закон Кеплера гласит о том, что орбиты любой планеты Солнечной системы представляет собой эллипс. Эксцентриситет определяет, насколько орбита отлична от окружности. Он равен отношению расстояния от центра эллипса (c) до его фокуса большой полуоси (a).
Эксцентриситеты объектов Солнечной Системы
Орбита Седны. В центре координат — Солнечная система, окруженная роем планет и известных объектов пояса Койпера.
В нашей системе орбиты планет ничем не примечательны. Самой «круговой» орбитой обладает Венера. Её афелий всего-лишь на 1,4 млн. км.больше перигелия, а эксцентриситет равен 0,007 (у Земли – 0,016). По довольно вытянутой орбите движется Плутон. Обладая ε = 0,244, он временами приближается к Солнцу даже ближе чем Нептун. Однако, поскольку Плутон не так давно попал в разряд карликовых планет, самую вытянутую орбит среди планет теперь имеет Меркурий, обладающий ε = 0,204.
Среди карликовых планет наиболее примечательна Седна. Обладая ε = 0,86, она делает полный оборот вокруг Солнца почти за 12 тысяч лет, удаляясь от неё в афелии более чем на тысячу астрономический единиц. Однако даже это несравнимо с параметрами орбит долгопериодических комет. Периоды их обращения порой исчисляются миллионами лет, а многих из них и вовсе никогда не вернутся к Солнцу – т.е. обладают эксцентриситетом, большем 1. Облако Оорта может содержать триллионы комет, удалённых от Солнца на 50-100 тысяч астрономических единиц (0,5 – 1 световых лет). На таких расстояниях на нихмогут влиять другие звёзды и галактические приливные силы. Поэтому такие кометы могут обладать очень непредсказуемыми и непостоянными орбитами с самими различными эксцентриситетами.
Наконец, самым интересным является то, что даже Солнце обладает совсем ни круговой орбитой, как это может показаться на первый взгляд. Как известно, Солнце движется вокруг центра Галактики, проделывая свой путь за 223 млн. лет. Причём, из-за бесчисленного взаимодействия со звездами она получила довольно ощутимый эксцентриситет, равный 0,36.
Эксцентриситеты в других системах
Сравнение орбиты HD 80606 b с внутренними планетами Солнечной системы
Открытие других солнечных систем неизбежно влечёт открытие планет с очень причудливыми параметрами орбит. Примером тому служат эксцентричные юпитеры, газовые гиганты с довольно высокими эксцентриситетами. В системах, имеющие такие планеты невозможно существование планет, подобных Земле. Они неизбежно упадут на гиганты или же статут их спутниками.
Среди обнаруженных на данный момент эксцентричных юпитеров самым большим эксцентриситетом обладает HD 80606b. Он движется вокруг звезды чуть меньшей, чем наше Солнце. Эта планета в перигелии приближается к звезде в 10 раз ближе, чем Меркурий к Солнцу, тогда как в афелии она удаляется от неё почти на астрономическую единицу. Таким образом, она имеет эксцентриситет 0,933.
Стоит отметить, что хоть данная планета и пересекает зону жизни, ни о каких видах привычной биосферы не может идти и речи. Её орбита создаёт на планете экстремальный климат.За короткий период сближения со звездой температура её атмосферы за считанные часы меняется на сотни градусов, в результате чего скорость ветров достигают многих километров в секунду. Подобными условиями обладают прочие планеты с высокими коэффициентами. Тот же Плутон, к примеру, при приближение к Солнцу приобретает обширную атмосферу, которая оседает в виде снега при удалении. В тоже время все Землеподобные планеты обладают орбитами, близкими к круговым. Поэтому эксцентриситет можно назвать одним из параметров, определяющим возможность наличия органической жизни на планете.
Орбитальный эксцентриситет
Содержание
Определение [ править ]
Эксцентриситет может принимать следующие значения:
Эксцентриситет e определяется выражением
е знак равно 1 + 2 E L 2 м красный α 2 <\ displaystyle e = <\ sqrt <1 + <\ frac <2EL ^ <2>>
или в случае силы тяжести:
е знак равно 1 + 2 ε час 2 μ 2 <\ Displaystyle е = <\ sqrt <1 + <\ frac <2 \ varepsilon h ^>> <\ mu ^ <2>>>>>>
Радиальные траектории классифицируются как эллиптические, параболические или гиперболические в зависимости от энергии орбиты, а не эксцентриситета. Радиальные орбиты имеют нулевой угловой момент и, следовательно, эксцентриситет равен единице. Сохранение постоянной энергии и уменьшение углового момента, эллиптическая, параболическая и гиперболическая орбиты стремятся к соответствующему типу радиальной траектории, в то время как e стремится к 1 (или в параболическом случае остается 1).
Для силы отталкивания применима только гиперболическая траектория, включая радиальный вариант.
Этимология [ править ]
Расчет [ править ]
Эксцентриситет эллиптической орбиты также можно использовать для получения отношения перицентра к апоапсису :
Для годовой орбитальной траектории Земли соотношение r a / r p = наибольший_радиус / наименьший_радиус ≈ 1,034 относительно центральной точки пути.
Примеры [ править ]
| Объект | эксцентриситет |
|---|---|
| Тритон | 0,000 02 |
| Венера | 0,006 8 |
| Нептун | 0,008 6 |
| земной шар | 0,016 7 |
| Титан | 0,028 8 |
| Уран | 0,047 2 |
| Юпитер | 0,048 4 |
| Сатурн | 0,054 1 |
| Луна | 0,054 9 |
| 1 Церера | 0,075 8 |
| 4 Веста | 0,088 7 |
| Марс | 0,093 4 |
| 10 Гигея | 0,114 6 |
| Makemake | 0,155 9 |
| Хаумеа | 0,188 7 |
| Меркурий | 0,205 6 |
| 2 Паллада | 0,231 3 |
| Плутон | 0,248 8 |
| 3 Юнона | 0,255 5 |
| 324 Бамберга | 0,340 0 |
| Эрис | 0,440 7 |
| Нереида | 0,750 7 |
| Седна | 0,854 9 |
| Комета Галлея | 0,967 1 |
| Комета Хейла-Боппа | 0,995 1 |
| Комета Икея-Секи | 0,999 9 |
| C / 1980 E1 | 1.057 |
| ʻOumuamua | 1,20 [а] |
| C / 2019 Q4 (Борисов) | 3,5 [б] |
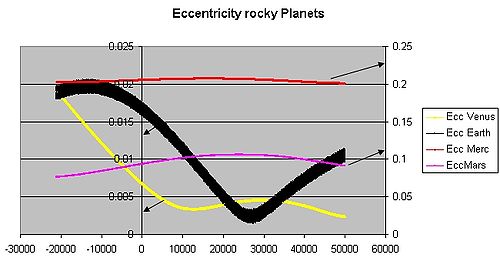
Эксцентриситет Земли орбиты «S в настоящее время около 0,0167; орбита Земли почти круглая. У Венеры и Нептуна эксцентриситет еще ниже. За сотни тысяч лет эксцентриситет земной орбиты изменяется от почти 0,0034 до почти 0,058 в результате гравитационного притяжения планет (см. График ). [1]
Большинство астероидов Солнечной системы имеют эксцентриситет орбиты от 0 до 0,35 со средним значением 0,17. [2] Их сравнительно высокие эксцентриситеты, вероятно, связаны с влиянием Юпитера и прошлыми столкновениями.
Средний эксцентриситет [ править ]
Климатический эффект [ править ]
Экзопланеты [ править ]
СОДЕРЖАНИЕ
Определение
Эксцентриситет может принимать следующие значения:
Эксцентриситет e определяется выражением
е знак равно 1 + 2 E L 2 м красный 3 α 2 <\ displaystyle e = <\ sqrt <1 + <\ frac <2EL ^ <2>>
( α отрицательно для силы притяжения, положительно для силы отталкивания; см. также задачу Кеплера )
или в случае силы тяжести:
е знак равно 1 + 2 ε час 2 μ 2 <\ displaystyle e = <\ sqrt <1 + <\ frac <2 \ varepsilon h ^>> <\ mu ^ <2>>>>>>>
Радиальные траектории классифицируются как эллиптические, параболические или гиперболические в зависимости от энергии орбиты, а не эксцентриситета. Радиальные орбиты имеют нулевой угловой момент и, следовательно, эксцентриситет равен единице. Сохранение постоянной энергии и уменьшение углового момента, эллиптические, параболические и гиперболические орбиты стремятся к соответствующему типу радиальной траектории, в то время как e стремится к 1 (или, в параболическом случае, остается 1).
Для силы отталкивания применима только гиперболическая траектория, включая радиальный вариант.
Этимология
Расчет
Эксцентриситет эллиптической орбиты также можно использовать для получения отношения радиуса перицентра к радиусу апоапсиса :
Примеры
| Объект | эксцентриситет |
|---|---|
| Тритон | 0,000 02 |
| Венера | 0,006 8 |
| Нептун | 0,008 6 |
| Земля | 0,016 7 |
| Титан | 0,028 8 |
| Уран | 0,047 2 |
| Юпитер | 0,048 4 |
| Сатурн | 0,054 1 |
| Луна | 0,054 9 |
| 1 Церера | 0,075 8 |
| 4 Веста | 0,088 7 |
| Марс | 0,093 4 |
| 10 Гигиея | 0,114 6 |
| Makemake | 0,155 9 |
| Хаумеа | 0,188 7 |
| Меркурий | 0,205 6 |
| 2 Паллада | 0,231 3 |
| Плутон | 0,248 8 |
| 3 Юнона | 0,255 5 |
| 324 Бамберга | 0,340 0 |
| Эрис | 0,440 7 |
| Нереида | 0,750 7 |
| Седна | 0,854 9 |
| Комета Галлея | 0,967 1 |
| Комета Хейла-Боппа | 0,995 1 |
| Комета Икея-Секи | 0,999 9 |
| C / 1980 E1 | 1.057 |
| ʻOumuamua | 1,20 |
| C / 2019 Q4 (Борисов) | 3.5 |
Эксцентриситет земной орбиты в настоящее время составляет около 0,0167; его орбита почти круглая. У Венеры и Нептуна эксцентриситеты еще меньше. За сотни тысяч лет эксцентриситет земной орбиты изменяется от почти 0,0034 до почти 0,058 в результате гравитационного притяжения планет.
Большинство астероидов Солнечной системы имеют эксцентриситет орбиты от 0 до 0,35 со средним значением 0,17. Их сравнительно высокие эксцентриситеты, вероятно, связаны с влиянием Юпитера и прошлыми столкновениями.
Средний эксцентриситет
Климатический эффект
Экзопланеты
Орбитальный эксцентриситет
Содержание
Определение [ править ]
Эксцентриситет может принимать следующие значения:
Эксцентриситет e определяется выражением
е знак равно 1 + 2 E L 2 м красный α 2 <\ displaystyle e = <\ sqrt <1 + <\ frac <2EL ^ <2>>
или в случае силы тяжести:
е знак равно 1 + 2 ε час 2 μ 2 <\ Displaystyle е = <\ sqrt <1 + <\ frac <2 \ varepsilon h ^>> <\ mu ^ <2>>>>>>
Радиальные траектории классифицируются как эллиптические, параболические или гиперболические в зависимости от энергии орбиты, а не эксцентриситета. Радиальные орбиты имеют нулевой угловой момент и, следовательно, эксцентриситет равен единице. Сохранение постоянной энергии и уменьшение углового момента, эллиптическая, параболическая и гиперболическая орбиты стремятся к соответствующему типу радиальной траектории, в то время как e стремится к 1 (или, в параболическом случае, остается 1).
Для силы отталкивания применима только гиперболическая траектория, включая радиальный вариант.
Этимология [ править ]
Расчет [ править ]
Эксцентриситет эллиптической орбиты также можно использовать для получения отношения перицентра к апоапсису :
Для годовой орбитальной траектории Земли соотношение r a / r p = наибольший_радиус / наименьший_радиус ≈ 1,034 относительно центральной точки пути.
Примеры [ править ]
| Объект | эксцентриситет |
|---|---|
| Тритон | 0,000 02 |
| Венера | 0,006 8 |
| Нептун | 0,008 6 |
| земной шар | 0,016 7 |
| Титан | 0,028 8 |
| Уран | 0,047 2 |
| Юпитер | 0,048 4 |
| Сатурн | 0,054 1 |
| Луна | 0,054 9 |
| 1 Церера | 0,075 8 |
| 4 Веста | 0,088 7 |
| Марс | 0,093 4 |
| 10 Гигея | 0,114 6 |
| Makemake | 0,155 9 |
| Хаумеа | 0,188 7 |
| Меркурий | 0,205 6 |
| 2 Паллада | 0,231 3 |
| Плутон | 0,248 8 |
| 3 Юнона | 0,255 5 |
| 324 Бамберга | 0,340 0 |
| Эрис | 0,440 7 |
| Нереида | 0,750 7 |
| Седна | 0,854 9 |
| Комета Галлея | 0,967 1 |
| Комета Хейла-Боппа | 0,995 1 |
| Комета Икея-Секи | 0,999 9 |
| C / 1980 E1 | 1.057 |
| ʻOumuamua | 1,20 [а] |
| C / 2019 Q4 (Борисов) | 3,5 [б] |
Эксцентриситет Земли орбиты «S в настоящее время около 0,0167; орбита Земли почти круглая. У Венеры и Нептуна эксцентриситет еще ниже. За сотни тысяч лет эксцентриситет земной орбиты изменяется от почти 0,0034 до почти 0,058 в результате гравитационного притяжения планет (см. График ). [1]
Большинство астероидов Солнечной системы имеют эксцентриситет орбиты от 0 до 0,35 со средним значением 0,17. [2] Их сравнительно высокие эксцентриситеты, вероятно, связаны с влиянием Юпитера и прошлыми столкновениями.