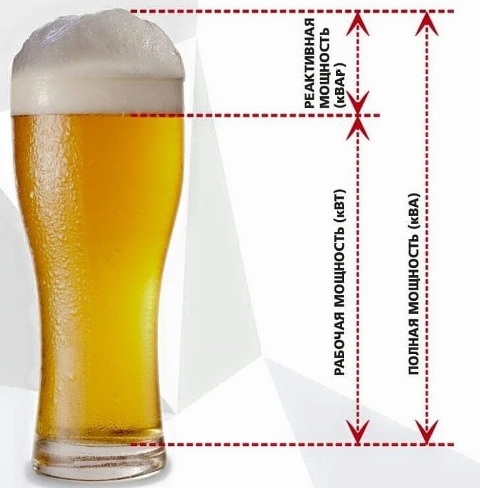
на что тратится реактивная мощность
Реактивная мощность — еще раз коротко о главном
Все чаще в различных изданиях и СМИ, в рамках информации о реализации Федерального закона от 23 ноября 2009 г. N 261-ФЗ «Об энергосбережении и о повышении энергетической эффективности…» встречается информация о борьбе с реактивной мощностью в сетевых компаниях и на промышленных предприятиях. Что же это за такое зло, что для борьбы с ним сетевыми компаниями тратятся сотни миллионов рублей, разрабатываются специальные долгосрочные целевые программы мероприятий по управлению реактивной мощностью в электрических сетях, ведутся агитации среди крупных потребителей электроэнергии на установку устройств по компенсации реактивной мощности. Так ли она важна и необходима эта компенсация?
Зачастую, многие потребители подсознательно полагают, что генерирующие компании поставляют два типа электрической энергии, так как оплачивают счета за потребленную активную и реактивную мощность, составляющие полной мощности выдаваемой генерирующими подстанциями. Хотя на самом деле понятие реактивной мощности хоть и общепринято и употребляемо, но не совсем корректно, так как физически реактивной мощности (именно в классическом понимании мощности, как отношения работы ко времени) не существует, так как никакой работы она не совершает.
Активная мощность — та часть электрической энергии, которая идет на совершение полезной работы и в процессе потребления преобразуется в другие типы энергии, например тепловую, механическую или световую.
Название реактивная мощность, по аналогии с реактивным сопротивлением, обусловлено способностью индуктивных и емкостных элементов накапливать и отдавать обратно в сеть, запасенную магнитную или электрическую энергию, и проявлять кажущиеся сопротивление только в цепях переменного тока. В то время как активное сопротивление зависит только от конкретного материала проводника.
Согласно общепринятому утверждению, под условным термином «реактивная мощность» понимают вторую составляющую полной мощности в сетях переменного тока, характеризующую интенсивность обмена/циркуляции электрической энергии между источником и подключенной к нему реактивной нагрузки (элементов индуктивности и/или конденсаторов), которая необходима только для расчетов определяющих влияние реактивных элементов на сеть.
Индуктивные (катушки в трансформаторах, дросселях, индукционных печах, двигателях и пр.) и емкостные (конденсаторные батареи) элементы практически не расходуют электроэнергии (без учета магнитного рассеивания и утечек в конденсаторах), хотя она и используется для создания электромагнитных и электрических/электростатических полей, но в процессе разряда возвращается обратно в сеть. Так как энергия циркулирует, то соответственно есть изменения тока и напряжения, которые можно посчитать в виде условной реактивной мощности используемой только для совершения данных преобразований.
Для электрических цепей в зависимости от подключаемого оборудования можно выделить три ситуации:

Рис. Диаграмма напряжения, тока и мощности для активной (резистивной) нагрузки.
Рис. Диаграмма напряжения, тока и мощности для индуктивной нагрузки.
Рис. Диаграмма напряжения, тока и мощности для емкостной нагрузки.
В реальности нагрузка имеет более-менее выраженную индуктивно-емкостную нагрузку (см. рис. ниже), зависящую от параметров самого оборудования. Из-за смещения фаз напряжения и тока уменьшается величина активной мощности, используемой для совершения полезной работы в системах с индуктивной нагрузкой, так как часть электрической энергии (реактивной мощности) будет циркулировать в энергосистеме и тратиться только на создание магнитных полей, не совершая ничего полезного, что в свою очередь приводит к увеличению тока необходимого для полноценной работы оборудования. В то же время, как известно, все проводники обладают активным сопротивлением, и циркуляция больших токов в системе будет приводить к их нагреву (величина нагрева, а соответственно и потерь, как известно, пропорциональна квадрату тока), а соответственно и к потерям электрической энергии.
Рис. Диаграмма напряжения, тока и мощности для индуктивно-емкостной нагрузки.
Для расчетов полной мощности применяется формула,
где, P — активная мощность, определяется по формуле,
Q — реактивная мощность, определяется по формуле,
U — напряжение, I — сила тока, ϕ — угол между напряжением и током.
Как было сказано выше, перетоки реактивной мощности в сети не выполняют полезной работы, при этом загружают источник, силовые линии, и все коммутационное оборудование, установленное между генерирующими станциями и конечными потребителями, а также нагревая кабели и линии высоковольтных передач, снижая тем самым их пропускную способность (с увеличением температуры растет сопротивление проводов) и создавая бесполезное тепло. Зачем же греть окружающую среду и еще платить за это деньги?
Помимо этого снижение пропускной способности и увеличение потерь из-за нагрева проводов ведет к значительным отклонениям напряжения, нормируемым в соответствии с ГОСТ 13109-97, что в конечном итоге негативно сказывается на:
Исходя из всего вышесказанного, решение проблем по компенсации реактивной мощности занимают одно из важнейших мест среди мероприятий направленных на повышение эффективности распределения, передачи и потребления электроэнергии. Ведь от их результатов зависит качественное электроснабжение, а также экономия средств по оплате за потребленную электроэнергию (активную и реактивную) и материальных ресурсов. Поэтому в зависимости от конкретной ситуации, все вопросы по компенсации реактивной мощности необходимо решать с учетом современных разработок и решений для данной области.
Основной безразмерной величиной, характеризующей преобладание реактивной составляющей в оборудование, является коэффициент мощности, который численно равен косинусу сдвига тока относительно приложенного к нагрузке напряжения или отношению потребляемой оборудованием активной мощности (Р), к полной (S).
Таким образом, многие предприятия и генерирующие/распределительные сетевые компании стремятся увеличить cos(ϕ) до 1, чтобы в значительной мере снизить величину потребляемой реактивной мощности. Как было приведено выше, в быту и промышленности в основном преобладает оборудование с индуктивным характером нагрузки, с отставанием тока от напряжения, поэтому используя устройства с емкостной нагрузкой, удается уменьшить сдвиг между током и напряжением в фазе, а соответственно добиться cos(ϕ), близкого к единице.
Этого можно достичь с минимальными затратами путем использования компенсирующих установок построенных на базе конденсаторов (конденсаторные установки КРМ, АУКРМ, батареи статических конденсаторов), более дорогих синхронных двигателей в режиме перевозбуждения или тиристорных схем с фильтрами, устанавливаемых непосредственно вблизи оборудования с преобладающей реактивной нагрузкой или группами, на распределительных подстанциях предприятия. Так создание электрической энергии с преобладающей емкостной характеристикой с генерирующих синхронными генераторами подстанций, в целом не целесообразно, ввиду тех же самых потерь при передаче и распределении электрической энергии.
В последнее время все более востребованными становятся конденсаторные установки АУКРМ, позволяющие производить более точную коррекцию коэффициента мощности с учетом изменения значений, потребляемой мощности от токов нагрузки, напряжения, времени суток.
При этом при формировании конденсаторной установки желательно обеспечивать максимально малый шаг регулирования, но с использованием минимального количества конденсаторов. В конечном итоге грамотный выбор определенного оборудования для компенсации реактивной мощности определяется на основании технико-экономических расчетов, характера преобладающей в сетях предприятия реактивной нагрузки, что позволит достигнуть положительного экономического эффекта при минимальных сроках окупаемости внедренного оборудования.
По материалам компании «Нюкон»
Что такое реактивная мощность и как с ней бороться
Реактивная мощность определяет периодический обмен электрической энергией между источником и электроприемником с двойной частотой по отношению к частоте переменного тока без преобразования ее в другой вид энергии и может рассматриваться как характеристика скорости обмена электроэнергией между источником и магнитным полем электроприемника.
Суммарная энергия, связанная с существованием этой составляющей мгновенной мощности, равна нулю. Ее появление, очевидно, связано с наличием в системе производства, передачи и распределения электроэнергии элементов, в которых возможно периодическое накопление и последующий возврат определенного количества энергии. В противном случае обмен электрической энергией между источником и электроприемником был бы невозможен.
Физика процесса и практика применения установок компенсации реактивной мощности
Чтобы разобраться с понятием реактивной мощности, вспомним сначала, что такое электрическая мощность. Электрическая мощность – это физическая величина, характеризующая скорость генерации, передачи или потребления электрической энергии в единицу времени.
Чем больше мощность, тем большую работу может совершить электроустановка в единицу времени. Измеряется мощность в ваттах (произведение Вольт х Ампер). Мгновенная мощность – это произведение мгновенных значений напряжения и силы тока на каком-то участке электрической цепи.
Физика процесса
В цепях постоянного тока значение мгновенной и средней мощности за какой-то промежуток времени совпадают, а понятие реактивной мощности отсутствует. В цепях переменного тока так происходит только в том случае, если нагрузка чисто активная. Это, например, электронагреватель или лампа накаливания. При такой нагрузке в цепи переменного тока фаза напряжения и фаза тока совпадают и вся мощность передается в нагрузку.
Если нагрузка индуктивная (трансформаторы, электродвигатели), то ток отстает по фазе от напряжения, если нагрузка емкостная (различные электронные устройства), то ток по фазе опережает напряжение. Поскольку ток и напряжение не совпадают по фазе (реактивная нагрузка), то в нагрузку (потребителю) передается только часть мощности (полной мощности), которая могла бы быть передана в нагрузку, если бы сдвиг фаз был равен нулю (активная нагрузка).
Активная и реактивная мощности
Часть полной мощности, которую удалось передать в нагрузку за период переменного тока, называется активной мощностью. Она равна произведению действующих значений тока и напряжения на косинус угла сдвига фаз между ними (cos φ ).
Мощность, которая не была передана в нагрузку, а привела к потерям на нагрев и излучение, называется реактивной мощностью. Она равна произведению действующих значений тока и напряжения на синус угла сдвига фаз между ними (sin φ).
Таким образом, реактивная мощность является величиной характеризующей нагрузку. Она измеряется в вольт амперах реактивных (вар, var). На практике чаще встречается понятие косинус фи, как величины характеризующей качество электроустановке с точки зрения экономии электроэнергии.
Действительно, чем выше cos φ, тем больше энергии, подаваемой от источника, попадает в нагрузку. Значит можно использовать менее мощный источник и меньше энергии пропадает зря.
Реактивная мощность может рассматриваться как характеристика скорости обмена электрической энергией между источником и магнитным полем электроприемника. В отличие от активной мощности реактивная мощность не выполняет непосредственно полезной работы, она служит для создания переменных магнитных полей в индуктивных электроприемниках (например, в асинхронных двигателях, силовых трансформаторах и др.), непрерывно циркулируя между источником и потребляющими ее электроприемниками.
Реактивная мощность бытовых потребителей
Итак, потребители переменного тока имеют такой параметр, как коэффициент мощности cosφ.
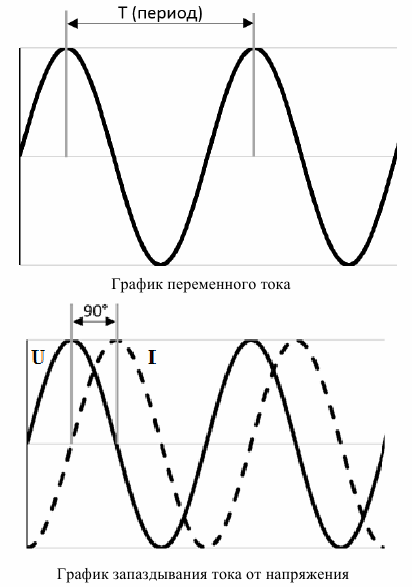
На графике ток сдвинут на 90° (для наглядности), то есть на четверть периода. Например, электрооборудование имеет cosφ = 0,8, что соответствует углу arccos 0,8 ≈ 36.8°. Этот сдвиг происходит из-за наличия в потребителе электроэнергии нелинейных компонентов – ёмкостей и индуктивностей (например, обмотки электродвигателей, трансформаторов и электромагнитов).
Для дальнейшего понимания происходящего требуется учет того факта, что, чем выше коэффициент мощности (максимум 1), тем более эффективно потребитель использует получаемую из сети электроэнергию (то есть большее количество энергии преобразуется в полезную работу) – такую нагрузку называют резистивной.
При резистивной нагрузке ток в цепи совпадает с напряжением. А при низком коэффициенте мощности нагрузку называют реактивной, то есть часть потребляемой мощности не совершает полезной работы.
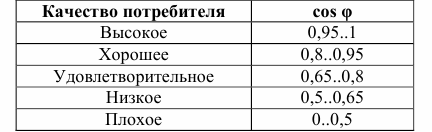
Таблица ниже демонстрирует классификацию потребителей по коэффициенту мощности.
Классификация потребителей переменного тока
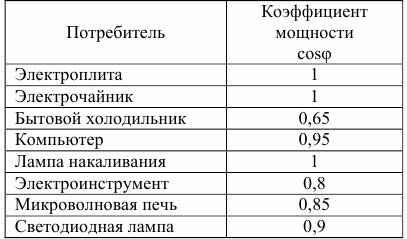
Следующая таблица демонстрирует коэффициент мощности распространённых в быту потребителей электроэнергии.
Коэффициент мощности бытовых электроприборов
Юмор электрика
Что такое реактивная мощность? Все очень просто!
Способы компенсации реактивной мощности

Экономический эффект от компенсации реактивной мощности
Экономический эффект от внедрения установок компенсации реактивной мощности может быть очень большим. По статистике он составляет от 12 до 50% от оплаты электроэнергии в различных регионах России. Установка компенсации реактивной мощности окупается не более чем за год.
Для проектируемых объектов внедрение конденсаторной установки на этапе разработки позволяет экономить на стоимости кабельных линий за счет снижения их сечения. Автоматическая конденсаторная установка, например, может поднять cos φ с 0.6 до 0.97.
Выводы

Вот несколько причин, по которым это происходит.
1. Уменьшение нагрузки на силовые трансформаторы, увеличение в связи с этим срока их службы.
2. Уменьшение нагрузки на провода и кабели, возможность использования кабелей меньшего сечения.
3. Улучшение качества электроэнергии у электроприемников.
4. Ликвидация возможности штрафов за снижение cos φ.
5. Уменьшение уровня высших гармоник в сети.
6. Снижение уровня потребления электроэнергии.
Что такое реактивная мощность и как её рассчитать?
Многие потребители электроэнергии не подозревают того, что часть учтённого электричества расходуется бесполезно. В зависимости от вида нагрузки уровень потерь электроэнергии может достигать от 12 до 50%. При этом счетчики электроэнергии засчитывают эти потери, относя их к полезной работе, за что приходится платить. Виной завышения оплаты за потребление электроэнергии, не выполняющей полезной работы, является реактивная мощность, присутствующая в сетях переменных токов.
Чтобы понять, за что мы переплачиваем и как компенсировать влияние реактивных мощностей на работу электрических установок, рассмотрим причину появления реактивной составляющей при передаче электроэнергии. Для этого придётся разобраться в физике процесса, связанного с переменным напряжением.
Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
К устройствам с индуктивными нагрузками относятся:
Ёмкостными сопротивлениями обладают конденсаторы.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению (см. рис.1).
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.

Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
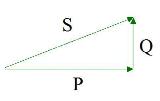
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.

Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:

Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Формулы
Поскольку реактивная мощность зависит от угла φ, то для её вычисления применяется формула: Q = UI×sin φ. Единицей измерения реактивной составляющей является вар или кратная ей величина – квар.
Активную составляющую находят по формуле: P = U*I×cosφ. Тогда
Зная коэффициент Pf (cos φ), мы можем рассчитать номинальную мощность потребителя тока по его номинальному напряжению, умноженному на значение силы потребляемого тока.
Способы компенсации
Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.
Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.
На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.

Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).

Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.
Нужны ли устройства компенсации в быту?
На первый взгляд в домашней сети не должно быть больших реактивных токов. В стандартном наборе бытовых потребителей преобладают электрическая техника с резистивными нагрузками:
Коэффициенты мощности современной бытовой техники, такой как телевизор, компьютер и т.п. близки к 1. Ими можно пренебречь.
Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.
Экономический эффект от установки таких устройств ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15% средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не электроэнергию.
Попутно вы решите следующие вопросы:
Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.