на что похожа фигура треугольник
Презентация «Игра «Найди предмет, похожий на треугольник»
Если ребёнок захочет повторить свой успех, то на последнем слайде также необходимо нажать на треугольник в правом нижнем углу слайда и игра начнётся сначала.
Прикреплённые файлы:


Дидактическая игра-занятие «Отгадай предмет» (младшая группа) Дидактическая игра-занятие «Отгадай предмет» младшая группа (дети 3–4 года) Цель игры: описывать предметы,выделяя признаки: материал, основные.
Игра «Найди клад» Задачи: 1. Развивать у детей умение ориентироваться на местности используя рисунок (карту). 2. Формировать дружеские и доброжелательные.
Презентация «Игра «Найди лишнее» для развития мышления и речи дошкольников» Мышление — это процесс анализа и систематизации новой информации об окружающем мире, полученной с помощью органов чувств. Человек наделен.
Презентация к дидактической игре по математике «Найди на картинке и сосчитай» для детей 6–7 лет Презентация к дидактической игре по математике «Найди на картинке и сосчитай» для детей 6-7 лет. Назначение игры – закрепление знаний детей.
Основные геометрические фигуры
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.
Окружность — это граница круга.
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Фигуры. Дидактические карточки.
Занятия с карточками помогут вам познакомить ребенка с окружающим миром, развить речевые умения, научить сравнивать, классифицировать, обобщать.
От 6 месяцев:
Показывайте карточки быстро, четко называя нарисованный предмет. Комплект показывать несколько дней, затем заменить новым. Через некоторое время повторить показ.
От 3 лет:
• Рассмотрите с ребенком карточки. Объясните ребенку, что существуют плоские и объемные геометрические фигуры. Предложите ему разделить карточки на две группы — с плоскими и объемными фигурами. Вместо с ребенком найдите сходство и отличие между этими группами.
•За одно занятие подробно изучайте с ребенком одну фигуру:
— расскажите ребенку об этой геометрической фигуре, задавай те ему вопросы;
— при объяснении пользуйтесь готовыми изображениями фигур; рисуйте их вместо с ребенком на листе бумаги; находите с ребенком объемные геометрические тела среди предметов домашнего обихода.
• Попросите ребенка подобрать для объемных геометрических тел плоские геометрические фигуры (шар — круг, квадрат — куб и т.п.)
•Помогите ребенку «создать» объемные геометрические фигуры. Попробуйте получить «тела вращения», поворачивая плоские геометрические фигуры вокруг своей оси.
•Подробно опишите любую фигуру, нарисованную на картинках, не называя ее. Предложите ребенку догадаться, о чем идёт речь, и подобрать соответствующую карточку. Затем поменяйтесь с ребенком местами: он описывает — вы отгадываете.
•Попросите ребенка сгруппировать карточки по разным признакам, найти общее и различное у всех фигур.
• Если ребенок уже учится читать, отрежьте названия, перемешайте и предложите подобрать названия к картинкам.
• Имея несколько наборов, можно играть в логические игры:
— классификация (сортировать карточки по тематике, подбирать обобщающее название);
— четвертый лишний (из четырех карточек: три на одну тему и одна на другую, ребенок должен выбрать лишнюю и объяснить свой выбор).
Расскажите детям о геометрических фигурах
Треугольник — плоская геометрическая фигура. Называется она так потому, что имеет три угла. Именно из этого определения и происходит название фигуры.
Изобразить треугольник несложно. На листе бумаги нужно поставить три точки и соединить их между собой отрезками. Эти отрезки будут называться сторонами треугольника. Всего у этой фигуры три стороны.
разносторонним, если все стороны фигуры разные. Углы такого треугольника будут тоже разными. Если две стороны треугольника образуют прямой угол (ровно 90°), то это — прямоугольный треугольник.
Треугольник считается простейшим многоугольником. Подумай и скажи, какие еще многоугольники ты знаешь? Конечно, это квадрат, ромб, трапеция, прямоугольник, параллелограм. Чем они отличаются от треугольника?
Вспомни, какие предметы треугольной формы ты знаешь?
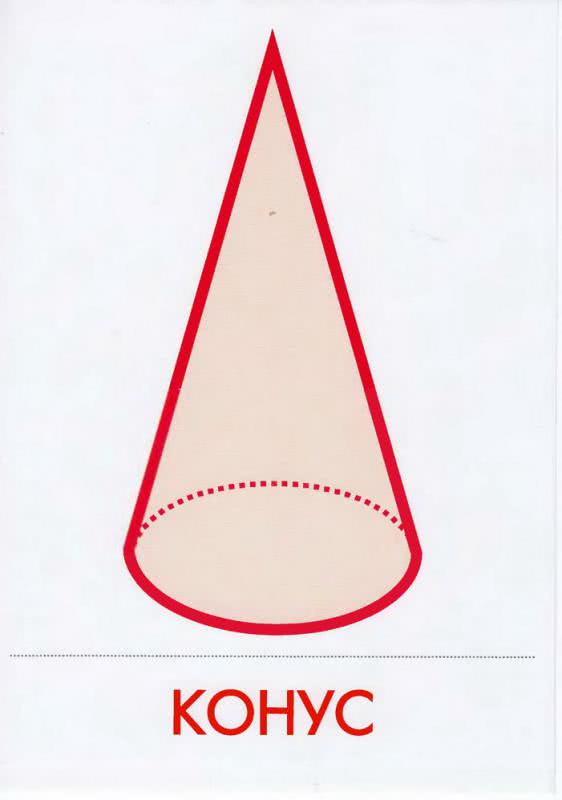
Конус — это объемная геометрическая фигура — геометрическое тело. Ее название пришло к нам из латинского языка, где звучало так же — «конус». Но, скорее всего, в латинский язык это слово попало из греческого языка. Древние греки именовали «коносами» еловые шишки. Ведь они по форме очень похожи на эту геометрическую фигуру.
Основанием конуса является круг или эллипс. Поэтому конус не имеет углов. Как ты думаешь, в какую фигуру превратится конус, если его основанием станет какой-либо многоугольник? Правильно, получится пирамида. Давай сравним эти фигуры. В чем они схожи? Чем отличаются?
Конус является фигурой вращения, то есть, образован он при помощи вращения прямоугольного треугольника. Возьми прямоугольный треугольник, поставь одной стороной прямого угла на стол и поверни вокруг оси. Та сторона, которая прижата к столу, будет описывать круг; вторая сторона — ось — будет неподвижна; а третья сторона будет при вращении создавать боковую стенку конуса.
Поверхность конуса состоит из множества отрезков, идущих от его вершины к основанию. Каждый отрезок называется образующей конуса. Образующие очень плотно расположены друг к другу. Получается сплошная поверхность. Она называется образующая или боковая. Точка, из которой расходятся образующие, является вершиной конуса. Покажи, пожалуйста, на картинке, где основание конуса, его боковая поверхность и вершина.
Конусы бывают разные, осе зависит от того, какая геометрическая фигура является основанием конуса. Если это круг, то конус будет называться круговым. Если в основании эллипс, то — эллиптическим.
Различают конусы и по другому признаку: насколько вершина совпадает с центром основания фигуры. Если из вершины конуса опустить отрезок перпендикулярно его основанию, и этот отрезок попадет точно в центр основания, значит конус прямой. И наш отрезок будет называться осью конуса. Когда точного попадания в центр основания нет, конус будет называться косым или наклонным. А если отрезать конусу верхушку, то мы получим две фигуры — конус и усеченный конус.
Подумай и скажи, какие предметы конической формы ты знаешь? Интересно!
У ромба четыре угла и столько же сторон. Как ты думаешь, ромб относится к четырехугольникам? Конечно, относится. А какие еще четырехугольники ты знаешь? Правильно, квадрат и прямоугольник. Чем ромб отличается от этих геометрических фигур?
Все стороны ромба всегда равны. Располагаются они параллельно друг другу. Поэтому ромб относится к параллелограммам. Подумай и скажи, какие еще параллелограммы ты знаешь? Правильно, это прямоугольник, квадрат.
Посмотри внимательно на картинку и скажи, равны ли между собой углы ромба? Правильно, они равны попарно. Покажи, пожалуйста, какие углы равны? А как ты думаешь, что будет, если мы все углы ромба сделаем одинаковыми? Правильно, у нас получится не ромб, а квадрат. Выходит, что ромб с прямыми углами называется квадратом.
Предметы, форма которых напоминает ромб, называются ромбовидными. Вспомни, какие ромбовидные предметы ты знаешь?
Круг — плоская геометрическая фигура. Нарисовать круг можно с помощью специального чертежного инструмента, который называется циркуль.
Если циркуля нет, можно сделать проще: взять стакан, приложить его ободком к бумаге и аккуратно обвести карандашом. У нас получится круг. Давай внимательно посмотрим на картинку. У нас есть лист бумаги, на котором нарисован круг. Это плоскость. Есть линия, которой обозначены границы круга.
Это окружность. А где центр круга? Покажи его, пожалуйста. Правильно, центр круга находится внутри нашей окружности. Получается, что часть плоскости, которая ограничена окружностью и содержит ее центр, и есть круг.
Все точки окружности удалены от центра круга на одинаковое расстояние. Это и делает круг круглым. Подумай и скажи, какие похожие геометрические фигуры ты знаешь. Правильно, это шар или сфера. Все точки сферы тоже удалены от ее центра на одинаковое расстояние. Чем шар отличается от круга? Конечно, объемом. Как ты думаешь, можно ли с помощью круга образовать шар? Правильно, можно. Если мы будем крутить круг вокруг его диаметра, то получим шар.
Диаметр круга — это отрезок, который соединяет две точки окружности и проходит через центр фигуры. Покажи, пожалуйста, на картинке, где диаметр нашего круга. Половина диаметра называется радиусом. Он соединяет центр и любую точку окружности.
Давай теперь вспомним объемные геометрические фигуры, кроме шара, основанием для которых может быть круг. Правильно, это конус и цилиндр.
Посмотри вокруг и назови предметы, которые умеют круглую форму. Какие из них можно назвать кругом, а какие шаром? Почему ты так думаешь?
Полукруг — плоская геометрическая фигура. Ее название говорит само за себя. Приставка «полу» означает, что эта фигура только наполовину является кругом.
Что ж, проверим, насколько это так. Давай посмотрим, как образуется полукруг. Для этого мы разделим круг пополам. У нас получилось два одинаковых полукруга. Как ты думаешь, сколько из одного круга можно сделать полукругов? Правильно, только два. Подумай, а могут ли существовать «полуквадрат» или «полутреугольник». Почему? Попробуй разделить эти геометрические фигуры пополам. Что получилось?
Теперь, давай внимательно посмотрим на картинку и определим основные особенности полукруга. Первая — одна сторона полукруга прямая. Это место рассечения круга на две равные части или линия диаметра круга. Вторая сторона полукруга скругленная. Еще одна особенность нашей фигуры в том, что у нее есть два угла. Покажи, пожалуйста, где они.
Как ты думаешь, какие предметы похожи на полукруг? Правильно, это может быть лук для стрельбы, долька арбуза. Объясни, чем они похожи?
Подумай и скажи, можем ли мы считать половину Луны полноценным полукругом? Конечно, нет. Луна — это планета. А все планеты, как мы знаем, по форме напоминают шар. Шар — это объемная геометрическая фигура. Следовательно, его половина тоже будет иметь объем. А полукруг какая фигура? Правильно, плоская. Хотя если мы нарисуем половинку Луны на бумаге, то можем смело назвать ее полукругом. Как ты думаешь, почему?
Овал — это плоская геометрическая фигура. Еще древние римляне заприметили, что в природе форму этой фигуры наиболее точно повторяет яйцо. В латинском языке слово «яйцо» звучало как «овум». От этого и происходит название этой геометрической фигуры — овал.
Давай внимательно посмотрим на картинку. Как ты думаешь, на какую другую геометрическую фигуру похож овал? Правильно, на круг. В чем именно их сходство? Правильно, обе фигуры не имеют углов и сторон. Обе плоские.
В отличие от круга овал не имеет ровной формы. В некоторых точках форма овала наиболее искривлена. Посмотри внимательно на картинку и покажи, пожалуйста, где эти точки. Конечно, в местах, где овал наиболее сплюснут и, наоборот, вытянут. Сколько этих точек? Правильно, в любом овале их четыре. И называются они вершинами овала.
У овала есть два диаметра. Отрезок, которым можно соединить две вершины овала, расположеные в местах, где фигура наиболее сплюснута, называется малым диаметром. Отрезок, соединяющий две противоположные вершины, — это большой диаметр. Покажи, пожалуйста, на картинке, где малый и большой диаметры нашего овала?
Предметы, форма которых напоминает овал, называются о вольными. Подумай и скажи, какие овальные предметы ты знаешь?
Шар — геометрическое тело. Получается он при вращении круга вокруг своего диаметра. Поэтому шар, в отличии от круга, — объемная фигура, фигура вращения. Это его первая особенность. Если разрезать шар пополам, то на срезе мы увидим круг. У шара нет ни сторон, ни углов. Это вторая его особенность.
Поверхность шара называется сферой. Это слово пришло к нам из греческого языка. Древние греки называли шар «сфайра». Сфера состоит из множества точек, удаленных от центра на одинаковое расстояние.
Как ты думаешь, а в природе встречаются предметы шарообразной (сферической) формы? Правильно, встречаются. Но в природе такие предметы скорее очень похожи на шар. Они не имеют такого четкого очертания, как геометрическая фигура. Посмотри на яблоко. Оно круглое. Но его форма не очень правильная. Подумай, что еще в природе похоже на шар?
Какие предметы имеют форму круга, а какие — форму шара? Почему ты так думаешь?
Пирамида — объемная геометрическая фигура. Ее название происходит от греческого слова «пирамис», которым древние греки и называли пирамиды.
Главная отличительная особенность пирамиды в том, что все ее грани всегда имеют форму треугольника. А вот в основании может лежать любой другой многоугольник. Все грани пирамиды сходятся в одной точке. Она называется вершиной пирамиды.
Существует немало видов пирамид. Все зависит от того, какой многоугольник является основанием фигуры. Если это треугольник, то по числу углов пирамида будет называться треугольной или трехгранной — по количеству граней. Если основанием пирамиды является квадрат, то соответственно пирамида будет называться четырехугольной или четырехгранной.
Этот список названия пирамид можно продолжать далее. До тех пор, пока количество углов многогранника не станет критическим. Тогда основание пирамиды постепенно превращается в круг, а сама фигура — в конус.
У каждой пирамиды есть высота. Это отрезок, который выходит из вершины пирамиды и опускается перпендикулярно к ее основанию.
Если вершина пирамиды проектируется прямо в центр ее основания, а основанием служит правильный многогранник, то такая пирамида называется правильной. У нее все грани являются одинаковыми равнобедренными треугольниками.
Подумай и скажи, какие предметы пирамидальной формы ты знаешь?
Прямоугольник — плоская геометрическая фигура. Называется она так из-за своей особенности: все углы у прямоугольника прямые, равны 90°.
Еще одна отличительная особенность прямоугольника заключается в том, что его стороны попарно равны. То есть каждые две противоположные стороны одинаковой длины.
Поскольку стороны прямоугольника расположены
параллельно друг к другу, прямоугольник еще называют параллелограммом. Это слово пришло к нам из греческого языка и было образовано от двух слов: «параллелос» — параллельный и «грамма» — линия.
Подумай и скажи, какие еще параллелограммы ты знаешь? Правильно, это ромб и квадрат. Чем они отличаются от прямоугольника? А в чем сходство этих фигур?
Как ты думаешь, треугольник можно назвать
параллелограммом? Конечно, нет. А почему ты сделал такой вывод? Правильно, потому что у параллелограмма обязательно должно быть четыре угла. Иначе стороны фигуры не могут быть параллельными. В этом его особенность. А у треугольника сколько углов?
Стороны прямоугольника одновременно являются его высотами. Давай представим, к примеру, два дома. Первый многоэтажный, с одним парадным. Второй, наоборот, невысокий, с несколькими парадными. Оба дома по форме являются прямоугольниками. Их параллельные стороны равны. При этом в случае с многоэтажным домом мы будем определять высоту по более длинной стороне прямоугольника. А высоту второго дома, наоборот, по более короткой.
Подумай и скажи, какие предметы прямоугольной формы ты знаешь?
Цилиндр — это объемная геометрическая фигура. Название происходит от греческого слова «цилиндрус». Так древние греки называли валик или каток. За схожесть формы с этими предметами геометрическая фигура стала именоваться цилиндром.
У этой геометрической фигуры два основания — сверху и снизу. Основания цилиндра равны и располагаются параллельно друг к другу.
Не всегда у цилиндра есть оба основания. Если у фигуры основание только внизу, то такой цилиндр называется открытым. Примером может быть стакан. Внизу у него плоскость. Это основание. А вверху — ничего. Стенки стакана, теоретически, можно продолжать до бесконечности.
У цилиндра есть высота. В прямом цилиндре она равняется длине отрезка от одного основания до другого.
Давай оглянемся по сторонам и посмотрим, какие предметы цилиндрической формы нас окружают? Подумай, что в природе имеет форму цилиндра?
У эллипсоида нет ни углов, ни сторон. Как ты думаешь, какую геометрическую фигуру он напоминает? Конечно, шар. Только у эллипсоида есть одна особенность. В отличии от шара, он немного сплюснут. Если разрезать эллипсоид, то можно увидеть овал и круг. Все зависит оттого, где разрезана фигура. Посмотри внимательно на рисунок. Как ты думаешь, где надо сделать разрез, чтобы форма среза напоминала круг? А где, чтобы получить овал? Эллипсоид является фигурой вращения, так как образуется при вращении овала (эллипса) вокруг своей оси.
Еще одна особенность эллипсоида в том, что у него есть три диаметра. Эти отрезки пересекаются в центре фигуры. Как ты думаешь, какие точки соединяет каждый отрезок? Два отрезка будут соединять точки в местах наибольшей выпуклости эллипсоида, один — в месте, где фигура несколько сплюснута. Все эти точки называются точками закругления эллипсоида.
Если разрезать эллипсоид ровно по диаметру, мы увидим плоскость. Она называется диаметральной. Как ты думаешь, сколько у эллипсоида может быть диаметральных плоскостей? Правильно, три. Почему ты так думаешь? Конечно, потому, что у эллипсоида три диаметра.
Подумай и скажи, какие ты знаешь предметы, которые по форме напоминают эллипсоид. Правильно, это может быть яйцо, слива, дыня. В природе очень много предметов эллиптической формы.
Трапеция — плоская геометрическая фигура. Название ее происходит от греческого слова «трапезион», которое переводится как «четырехугольник с неравными сторонами». Так древние греки именовали стол такой формы.
Трапеция — очень интересная фигура. Первая ее особенность состоит в том, что у трапеции только две из четырех сторон параллельны друг к другу. Эта пара сторон называется основаниями трапеции. Соответственно, две другие стороны — боковые.
Есть два вида трапеций. Первый — равнобокая или равнобедренная. У такой трапеции боковые стороны равны. Также у нее равны и углы при основании. Если одна из сторон меньше и располагается под прямым углом к основанию, то это уже второй вид трапеции — прямоугольная. Посмотри внимательно на картинку и скажи, какая трапецию у нас нарисована? Почему ты так думаешь?
Трапеция относится к многоугольникам. У нее четыре угла. Как ты думаешь, можно ли назвать трапецию параллелограммом? Конечно, нет. Несмотря на то, что у трапеции четыре угла, только две ее стороны параллельны друг другу. Какие геометрические фигуры, которые являются параллелограммами, ты помнишь? Правильно, это квадрат, прямоугольник, ромб. В чем сходство этих фигур с трапецией? В чем отличие?
Давай посмотрим вокруг себя. Какие предметы имеют форму трапеции? Они называются трапециевидными. Например, у человека есть трапециевидные мышцы, которые расположены в верхней части спины в районе лопаток.
Квадрат — плоская геометрическая фигура. Ее название происходит от латинского слова «квадратус», что в переводе означает «четырехугольный».
Давай вместе посчитаем, сколько углов у квадрата? Получилось четыре. Ровно столько у квадрата и сторон. Покажи на рисунке, где стороны квадрата.
Если внимательно посмотреть на фигуру, можно заметить ее отличительную особенность. Все стороны квадрата равны. Углы фигуры тоже равны. Такие углы называются прямыми.
За такую свою особенность квадрат считается правильным многоугольником. Давай вспомним другие геометрические фигуры: ромб и прямоугольник. Как ты думаешь, чем они похожи на квадрат? Конечно же, у них есть стороны и углы. Сколько углов и сторон? Правильно, по четыре. Кроме этого, ромб и прямоугольник — плоские геометрические фигуры. И в этом их еще одна схожесть с квадратом.
А теперь подумай и скажи, чем ромб и прямоугольник отличаются от квадрата? Правильно, у ромба нет прямых углов, хотя стороны фигуры равны. А у прямоугольника, наоборот, углы прямые, зато стороны имеют разную длину.
Вспомни и назови неживые предметы, имеющие квадратную форму? (Можно помочь ребенку: окно, столешница обеденного стола, рамка для фотографии, шахматная доска и т.д.). А что в природе напоминает по форме квадрат? Вспомнить сложно, не так ли. Это говорит о том, что для живых организмов квадратные формы не свойственны.
У параллелепипеда шесть сторон или граней, имеющих форму параллелограмма. Места соединения граней друг с другом называются ребрами. Всего у параллелепипеда 12 ребер. Ребра параллелепипеда соединяются в восьми точках. Эти точки называются вершинами. Покажи, пожалуйста, где вершины у нашего параллелепипеда. Сколько ребер соединяет каждая из них? Правильно, три.
Подумай и скажи, на какую геометрическую фигуру похож параллелепипед? Правильно, это куб. В чем сходство этих двух фигур? Чем они отличаются? Можно ли назвать куб параллелепипедом? Конечно, можно. Если у параллелепипеда грани имеют форму квадрата, то это куб.
Параллелепипед может быть прямым и наклонным. У прямого параллелепипеда четыре боковые грани имеют форму прямоугольника и располагаются перпендикулярно к плоскости основания фигуры. Если у прямого параллелепипеда все грани имеют форму прямоугольника, это — прямоугольный параллелепипед. Подумай и скажи, какие предметы имеют форму прямоугольного параллелепипеда. Конечно, это спичечная коробка, кирпич. Если в основание параллелепипеда мы положим ромб, то мы получим наклонный параллелепипед.
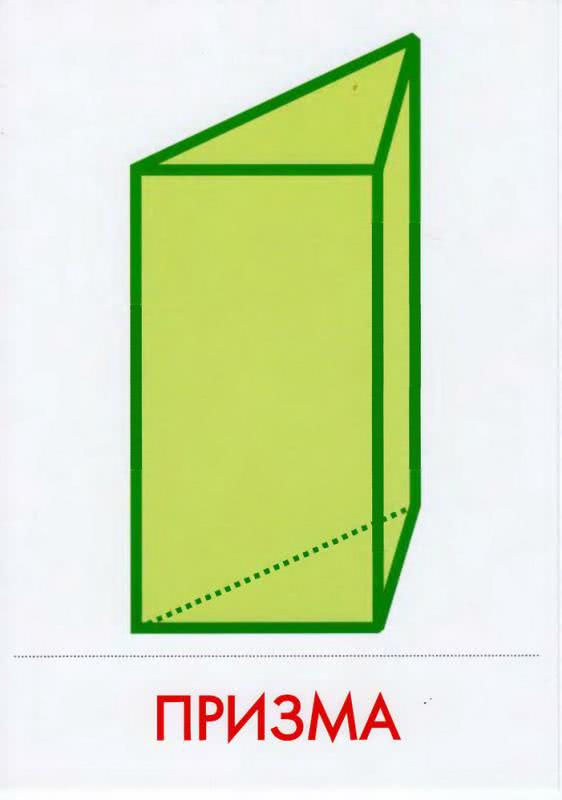
Призма — это объемная геометрическая фигура. Ее название происходит от греческого слова «присма». В переводе оно означает «опиленный».
У призмы есть два основания. Это две стороны или грани, расположенные снизу и сверху фигуры. Основаниями призмы всегда служат два одинаковых многогранника. Они параллельны. Боковые грани призмы представляют собой параллелелограммы. Подумай и скажи, на какую другую геометрическую фигуру похожа призма? Правильно, на параллелепипед. В чем их сходство? Скажи, пожалуйста, чем они отличаются друг от друга?
Все грани призмы соединяются между собой. Каждое такое соединение называется ребром фигуры. Все ребра призмы соединяются в точках, которые называются вершинами. Каждая вершина объединяет по три ребра. Количество ребер и вершин у призмы зависит от количества углов у многогранников, положенного в основание фигуры.
От того, какой многоугольник положен в основание призмы, зависит ее название. Например, если основанием служит треугольник, то призма будет называться треугольной. Если использован многоугольник с четырьмя углами, то, соответственно, и призма будет называться четырехугольной. Как ты думаешь, как будет называться призма, в основание которой положен пятиугольник?
Призма называется правильной, если основанием для нее служит правильный многоугольник. Скажи, как можно еще назвать призму, в основании которой лежит квадрат, а боковые грани являются параллелограммами? Правильно, можно сказать, что это параллелепипед. А если и основания призмы, и ее боковые грани являются квадратами? Конечно, это куб.
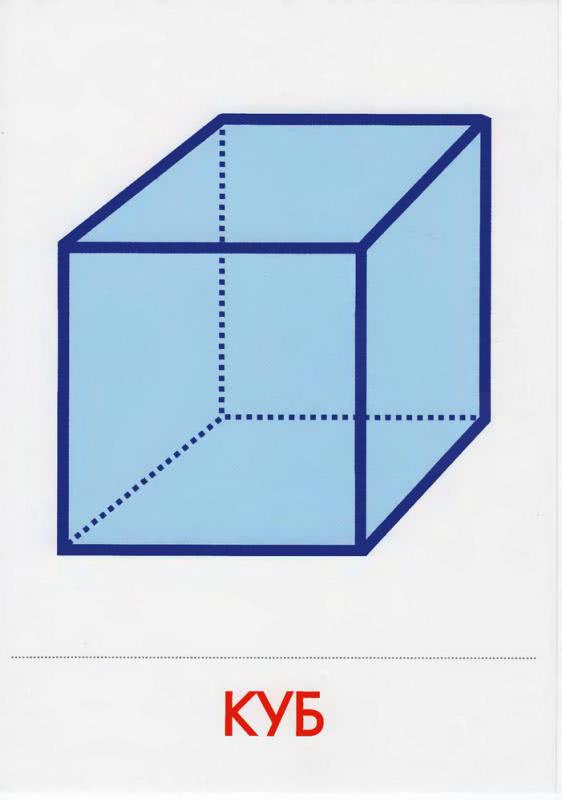
У куба есть шесть одинаковых сторон, имеющих форму квадрата. Эти стороны еще называют гранями куба. Соединение граней друг с другом называется ребром. Посмотри внимательно на картинку. Давай вместе посчитаем, сколько ребер у куба. Правильно, всего получается 12.
Ребра куба соединяются в нескольких точках. Эти точки называются вершинами фигуры. Покажи, пожалуйста, вершины куба. Сколько всего вершин? Правильно, восемь. В каждую вершину сходятся по три ребра куба.
Все ребра куба взаимно перпендикулярны. Благодаря этой особенности все грани фигуры имеют форму квадрата, у которого, как ты знаешь, все углы прямые, а стороны равные. Поэтому куб является правильным многогранником. Как ты думаешь, почему многогранник? Правильно, потому, что у куба много граней.
Какие еще многогранники ты знаешь? Конечно, это параллелепипед, призма, пирамида. Как ты думаешь, чем они отличаются от куба?
Куб иногда называют гексаэдром (от греч. «гекс» — шесть и «гедра» — основание, грань). Так древние греки называли шестигранник. И чаще всего речь шла именно о правильном шестиграннике, то есть кубе.
Подумай и скажи, какие предметы имеют форму куба? (Можно подсказать: кубик, тумба, комната, емкость для хранения круп и т.д.).