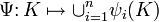на чем основана фрактальная графика
Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся и перспективных видов компьютерной графики.
Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.
Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского «fractus» и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале.
В центре фрактальной фигуры находится её простейший элемент — равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.
Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом можно описать и такой графический элемент как прямая.
Изменяя и комбинирую окраску фрактальных фигур, можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также составлять из полученных фигур «фрактальную композицию». Фрактальная графика, так же как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений ничего, кроме формулы, хранить не требуется.
Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.
Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект», «Фрактальная прямая», «Фрактальная композиция», «Объект-родитель» и «Объект наследник».
Следует обратить внимание на то, что фрактальная компьютерная графика как вид компьютерной графики двадцать первого века получила широкое распространение не так давно.
Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать множество приёмов: горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение? Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную композицию. Это свойство фрактального объекта может быть удачно использовано для создания орнамента или декоративной композиции. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу.
С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически, благодаря фрактальной графике, найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.
Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ.
Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например, Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.
Фрактальная графика
Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
Многие объекты в природе обладают фрактальными свойствами, например побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Содержание
История
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Примеры
Самоподобные множества с необычными свойствами в математике
Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:
Рекурсивная процедура получения фрактальных кривых
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены три первых шага этой процедуры для кривой Коха.
Примерами таких кривых служат:
Фракталы как неподвижные точки сжимающих отображений
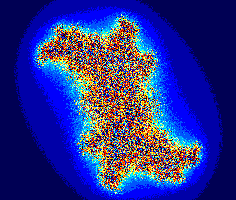
Свойство самоподобия можно математически строго выразить следующим образом. Пусть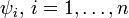 
— сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости: 
Можно показать, что отображение Ψ является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.
Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения 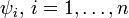— отображения подобия, а n — число звеньев генератора.
Фракталы в комплексной динамике
Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу XX века и связаны с именами Фату и Жюлиа.
Пусть F(z) — многочлен, z0 — комплексное число и рассмотрим следующую последовательность:
.
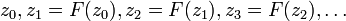
Нас интересует поведение этой последовательности при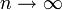 
. Эта последовательность может:
Ещё один известный пример такого рода — бассейны Ньютона.
Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.
Стохастические фракталы
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:
Фрактальная монотипия, или стохатипия — направления в изобразительном искусстве, состоящие в получении изображения случайного фрактала.
Созерцание великого фрактального подобия
(с) «Галактика галактик»
Фракталы — не просто красивое природное явление. Согласно проведенным исследованиям, рассматривание фрактальных структур на 60 % повышает стрессоустойчивость, измеряемую на основе физиологических показателей. При созерцании фракталов в лобной коре головного мозга всего за одну минуту увеличивается активность альфа-волн — как во время медитации или при ощущении легкой сонливости.
Неудивительно, что фрактальный биодизайн оказывает на человека умиротворяющее воздействие. Нам нравится смотреть на облака, на языки пламени в камине, на листву в парке… Как это работает? Ученые предполагают, что естественный ход поисковых движений наших глаз — фрактальный. При совпадении размерности траектории движения глаз и фрактального объекта мы впадаем в состояние физиологического резонанса, за счет чего активизируется деятельность определенных участков мозга.
Но не все фракталы одинаково полезны. В данной статье расскажем о фрактальной размерности и о её влиянии на здоровье.
Биофракталы
(с)
Примеры фракталов в природе встречаются повсеместно: от ракушек до сосновых шишек. Каждый фрактал имеет математическую размерность D. Для человека наиболее полезны фракталы с размерностью 1,3—1,5, и большинство фрактальных объектов, созданных природой, имеют именно такую размерность. А глаз человека эстетически «настроен» на восприятие как раз таких, встречающихся в природе фракталов.
Прекрасным примером фракталов в природе являются деревья. Фракталы можно обнаружить на каждом уровне лесной экосистемы — от семян и сосновых шишек до ветвей и листьев. На иллюстрации выше запечатлена «застенчивая крона» — явление, когда кроны деревьев не соприкасаются, формируя локальные участки лесного полога.
С биологической точки зрения такое расположение крон объясняется естественным отбором — листья расположены как можно дальше друг от друга, чтобы максимизировать доступ к ресурсам, особенно к солнечному свету для фотосинтеза.
Итальянская капуста романеско имеет сверхэффективную конструкцию, позволяющую максимизировать воздействие солнечного света и транспортировать питательные вещества по всей клеточной структуре растения.
Однако размерность этой капусты — 2,66. Вообще, дробная размерность является ключевой особенностью фракталов. При этом большинство из них находится в плоскости между линией (размерность 1) и двухмерной поверхностью (размерность 2). Чем выше показатель, тем больше движение в сторону трехмерных объектов (размерность 3).
Компьютерные игры
Трехмерные фракталы — одни из самых редких в природе. Гораздо проще встретить их в виртуальной реальности. Например, в игре Marble Marcher — уникальной аркаде, где нужно прокатить шар к цели в пространстве, созданном единым всеобъемлющим алгоритмом. Практически все, что вы увидите в игре, создано не дизайнерами, а чистой математикой.
Yedoma Globula — это 3D-песочница на самописном движке, в которой можно исследовать процедурно создаваемые фрактальные ландшафты.
Фрактальные формулы можно использовать в компьютерной графике для создания реалистичных гор, рек, лесов и облаков. Игра Everything пошла гораздо дальше: в ней помимо визуальной составляющей в системообразующей части геймплея использовано фрактальное подобие. Тут фактически нет NPC-персонажей. Вы можете начать игру в образе свиньи, которая бродит по зеленым склонам и встречает дуб, а затем стать дубом, который отправится в самостоятельное путешествие.
Гаджеты
Использовать фракталы как «что-то полезное» можно не только в компьютерных играх или для релаксации. Именно фракталы подсказали способ уменьшения размера антенн для сотовых телефонов. Фрактальная геометрия расширяет способность создавать новые, более практичные устройства.
Сейчас фракталы используются в новом поколении спутниковой связи, в устройствах IoT и других проектах приема, передачи и преобразования радиоволн.
Архитектура
Фракталы можно использовать даже неосознанно. На фото выше изображен фрагмент купола иранской мечети. А здесь вы найдете множество фотографий потолков школ, культурных и религиозных сооружений в Иране, которые демонстрируют невероятно сложные фрактальные рельефы и мозаики, декорирующие изысканные архитектурные элементы.
Храм Деви Джагадамби в Кхаджурахо — отличный пример фрактальной архитектуры. Индийские и многие другие храмы Юго-Восточной Азии имеют фрактальную структуру: главная башня окружена башнями меньшего размера, те в свою очередь — еще более маленькими башнями. И так до восьми (а порой и больше) уровней, представляющих различные аспекты индуистского мифологического пантеона.
Фракталы в архитектуре — не уникальное изобретение одной части света. Сложное убранство готической, ренессансной и барочной архитектуры, особенно выраженное в соборах, часто демонстрирует фрактальное копирование и масштабирование на нескольких уровнях. Характерное для европейской архитектуры с конца XII в. переплетение арок скорее имело не эстетическое, а практическое значение: оно было разработано для укрепления окон и стен против давления ветра.
С конца XX века фрактальную геометрию использовали осознанно для создания интересных и приятных глазу фасадов. На фото — здание одного из самых сложных в архитектурном плане комплексов, расположенное в мельбурнском городском районе (Австралия). В комплексе объединены культурные, рекреационные и коммерческие проекты.
Опасные фракталы
Большинство фрактальных изображений, генерируемых математическими, естественными и человеческими процессами, обладают общим эстетическим качеством, основанным на визуальной сложности. Участники тестов визуального восприятия предпочитают фракталы именно естественного происхождения с размерностью 1,3—1,5. Для примера: волны и облака имеют размерность 1,3, береговая линия — 1,05.
А что, если увеличить размерность? Получившийся объект не всегда будет приятно разглядывать. На иллюстрации выше изображена картина распределения электрического разряда с размерностью 1,75, известная как фигура Лихтенберга, созданная высоковольтным электрическим разрядом на непроводящем материале.
Еще один отталкивающий объект — фрактальный продукт кристаллических структур с размерностью 1,8, сфотографированный через микроскоп.
Демосцена & софт
Пожалуй, нигде так красочно не исследовали мир фракталов, как в демосцене. Hartverdrahtet — достойный победитель конкурса демосцены 2012 года по 4-килобайтным файлам. Автор, Demoscene Passivist, говорит, что для создания демо с процедурно генерируемыми фрактальными ландшафтами потребовалось около двух месяцев.
А вот один из лучших проектов с фрактальными эффектами в демосцене. К сожалению, качество демонстрационного видео крайне плохое (из-за давности лет), но демо можно скачать и запустить на компьютере.
Для создания подобных или других фрактальных миров особых ухищрений не требуется. Есть несколько отличных программ, с помощью которых вы сможете самостоятельно изучать особенности фрактальной вселенной.
XaoS Open Source Project. Бесплатный, открытый, кроссплатформенный инструмент для масштабирования и изучения множества Мандельброта и десятков других фракталов.
JWildfire. Еще одна кроссплатформенная (в том числе с мобильной версией) программа, основанная на Java с открытым исходным кодом, для обработки изображений. Она известна в основном своим сложным генератором пламенных фракталов.
Mandelbulber | Mandelbulb3D. Превосходные бесплатные инструменты для создания трехмерных фракталов, таких как устрашающая Оболочка Мандельброта, загадочная «коробка» Мандельбокс и др. Mandelbulber несколько более функционален и быстр, но Mandelbulb3D чуть проще в использовании.
По ссылке вы найдете множество других программ.
Фрактальная графика – популярное направление компьютерного рисунка
В век цифровых технологий все реже встречаются художники, рисующие кистью или карандашом. Большая часть людей этой профессии уже перешли на современные планшеты и специальный софт. Конечно же, живые рисунки ценятся по-прежнему высоко. Но игнорировать новые инструменты, которые предоставляет прогресс уже не получится. Фрактальная графика, растровая и векторная – это новый вид искусства. Особое место в компьютерном рисунке занимают фракталы. Они являются неким симбиозом математики и изобразительного искусства.
Фрактальная графика – что это?
Сегодня фрактальная графика – это одна из самых современных и продвинутых технологий создания компьютерных изображений. Состоят такие рисунки из фракталов – особых структур, представляющих собой сложную сеть самоподобных фрагментов. Если взять небольшой элемент фрактала, то можно получить четкое представление обо всем объекте.
Каждый из нас уже встречался с фрактальной графикой. К ней можно смело отнести узоры на коврах, висевших на стенах в каждой советской квартире. Сегодня на многих сайтах можно встретить заставки или рисунки из повторяющихся по форме элементов.
Фрактальная графика природных объектов
Самым наглядным примером фрактальной графики в природе можно назвать капусту Романеско. Это довольно распространенный продукт в Италии. По своему строению этот овощ похож на пирамиду, состоящую из маленьких таких-же пирамид. Каждая частичка этого фрактального растительного объекта повторяет свойства целого овоща.
Капуста Романеско не единственный пример. Свойствами фрактальной графики обладают многие объекты вокруг нас. Это: ветки деревьев, морские кораллы, облака, органы и системы человека. Они тоже являются по сути фракталами. Вспомните лишь как выглядят на картинках легкие, система кровеносных сосудов или мозг человека. Несмотря на очевидную сложность этих объектов, многие из них могут быть описаны простыми математическими формулами.
Уравнения
Компьютерной фрактальной графикой управляют математические уравнения. Стоит изменить в каком-то из них хоть один коэффициент, и уже получается совсем другое изображение. Эта математическая идея очень понравилась современным художникам. Ведь с помощью всего нескольких математических выражений можно задать линии, а также объемные объекты весьма замысловатой формы.
Фрактальная компьютерная графика – это современный способ создания абстрактных композиций, в которых появляется возможность реализовать множество приемов: горизонтали, вертикали, диагонали, симметрию, асимметрию. Все элементы этих объектов подобны, а в совокупности представляют собой сложную композицию. Люди научились этому относительно недавно. Но, в природе фрактальные формы существовали всегда. Самые простые их примеры – снежинки.
Что такое фракталы?
Сами по себе фракталы не имеют общепринятого строгого определения. К фрактальным формам относят объекты, если они обладают такими свойствами, как:
Софт для фрактальной графики
Сегодня существует специальный компьютерный софт, с помощью которого можно создавать рисунки с помощью фрактальной графики. Наиболее популярные из них:
Теперь вы представляете, что такое фрактал и фрактальная графика. И, возможно, отныне станете замечать больше подобных объектов вокруг себя.
Что такое Фрактальная графика?
В век информационных технологий все реже можно встретить художников, рисующих на лисе акварелью, маслом, карандашом. Увидеть мангак, закупающих килограммы скринтонов. Ведь большая часть художников уже перешла на планшеты и удобный софт. Наверное, правильно. Можно сколько угодно говорить:”Живые рисунки лучше, они пахнут краской.”, но нельзя отрицать новые возможности, которые дает прогресс. В статье Основы компьютерной графики мы говорили, что двумерную графику разделяют на векторную и растровую, хотя отдельно называют еще и фрактальный тип обособления изображений. Про фрактальную графику, графику слияния математики и искусства мы и поговорим в этой статье.
Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся и перспективных видов компьютерной графики. Логично, что Фрактальная графика состоит из фракталов. Но что же это такое? Фрактал — это структура самоподобных фрагментов. Это значит, что взяв небольшую часть фрактала можно получить информацию обо всем фрактале. Как повторяющиеся фоны на сайтах или узоры на советских коврах. Чтобы представить себе фрактал и запомнить как он выглядит на всю жизнь, достаточно посмотреть на Капусту Романеско. Это реально существующая итальянская капуста.
Капусты Романеско похожи на пирамиды, у них красивый светло-зеленый цвет и они не горчат в отличие от брокколи или цветной капусты.
Как мы видим на фотографии мелкие элементы фрактального объекта повторяют свойства всего объекта, а процесс наследования можно продолжать до бесконечности.
Изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать множество приёмов: горизонтали и вертикали, диагональные направления, симметрию и асимметрию. С чем можно сравнить фрактальное изображение? Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную композицию.
На самом деле фрактальные свойства имеет очень большое количество природных объектов — просто мало кто об этом задумывается. Вы можете любоваться облаками на небе, набегающими волнами прибоя, ходить по лесу — и даже не подозревать, что в основе этой красоты лежит математика. Несмотря на всю сложность природных объектов, многие из них в принципе описываются довольно простыми математическими формулами. Хотя в чистом виде фракталы в природе не существуют.
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Фигура является фракталом, если обладает следующими свойствами:
1. имеет нетривиальную структуру во всех масштабах (для фрактала увеличение масштаба не ведет к упрощению структуры, поэтому на всех шкалах мы увидим одинаково сложную картину).
2. является самоподобной или приближенно самоподобной.
3. имеет дробную метрическую размерность или метрическую размерность, превосходящую топологическую.
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений:
Apophysis 3D — используется fractal flame — алгоритм. В ней можно создавать как 2Д — изображения, так и псевдо 3Д — графику. На данный момент не поддерживается разработчиками.
Apophysis 7X — Логическое продолжение Apophysis 3D, но с поддержкой от разработчиков. Работать в программе нужно, манипулируя треугольниками. Есть генератор мутаций — случайное редактирование треугольников. Серьёзные возможности по трансформациям и практически всем параметрам фрактала.
Chaotica—Инструмент на основе fractal flame — алгоритма, но ориентированный более на рендеринг изображения.
Ultra Fractal — Мощный инструмент для фрактальных художников. Поддерживает слои, альфа-каналы, градиенты, создание собственных формул и многое другое.