на чем основан матричный метод оценки профрисков
Методы оценки профессиональных рисков: выбираем подходящий
Методы оценки профессиональных рисков: выбираем подходящий
На момент написания этой статьи методы оценки профессиональных рисков не утверждены ни Федеральными законами, ни постановлениями Министерств. Вместе с тем, необходимость в проведении этого мероприятия не исчезает и уже подчеркивается предписаниями Государственной инспекции по труду. Сегодня широкой публике представлены десятки способов оценить профессиональные риски: начиная с тех, что закреплены в ГОСТах и заканчивая авторскими методами экспертных организаций. Сегодня мы разберёмся, какие методы оценки профессиональных рисков подходят для определённых ситуаций, расскажем про их плюсы и минусы применения. Начнём!
Методы оценки профрисков: где их искать?
Несмотря на то, что тема профессиональных рисков далеко не новая, в 2019 году интерес организаций был сильно подогрет к проведению данной процедуры. Во-первых, введение риск-ориентированного подхода. Во-вторых, повышение уровня ответственности работодателей. В-третьих, штрафы после проверок инспекции по труду. Отсутствие единой утверждённой методики оценки профессиональных рисков (и вместе же с этим необходимость проведения) заставило работодателей искать любые зацепки в нормативной документации, строить логические догадки и перечитывать государственные стандарты. В итоге сформировался список документов, которые содержат методы оценки профессиональных рисков:
Чаще стали появляться и авторские методы оценки профессиональных рисков: мы с интересом отмечаем работы Т.В. Ригера (метод коэффициента безопасности труда), С.С. Тимофеевой (совершенствование современного законодательства в области охраны труда) и рады делиться собственными разработками — метод повышения объективности оценки профессионального риска (подготовлено и разработано специалистами ЦПР «Эксперт»).
Безусловно, это не окончательный список. В очень скором времени появится еще методы оценки профессиональных рисков, среди которых, как мы надеемся, будет единый, принятый на Федеральном уровне.
Запутались? Напишите нам, мы поможем. Бесплатно.
Матричные методы оценки профессиональных рисков
Пожалуй, самый простой и недорогостоящий метод оценки профессиональных рисков: работниками организации (или экспертами привлечённой организации) выполняется составление матрицы рисков, согласно которой риски оцениваются по схеме «вероятность — ущерб». Эксперт для каждой ситуации определяет, насколько вероятно её наступление и насколько велик потенциальный ущерб. В итоге составляется таблица, она же — матрица рисков: белые ячейки означают приемлемый риск, серый — высокий и черный — неприемлемый.
Матрица оценки профессиональных рисков
Вместе с простотой использования настоящего метода приходят и его минусы: такая экспертная оценка обладает очень низкой объективностью. Повысить этот показатель можно, привлекая экспертов сторонних организаций (ввиду их опыта), или же используя дисперсионный анализ объективности оценок (авторский метод ЦПР «Эксперт»).
Косвенные методы оценки профессиональных рисков
Этот метод будет очень кстати, если Ваша организация насчитывает в штате не более 10 человек, а основная деятельность не предполагает физического труда. Иными словами, этот метод, на наш взгляд, идеален для офисных (консалтинговых организаций).
Суть этого способа оценить профессиональные риски сводится к тому, чтобы найти соотношение между количеством опасных ситуаций и общим числом возможных исходов события. Центральной фигурой этого метода является индекс Элмери, который показывает, сколько % от пунктов безопасности соблюдается на предприятии.
Впрочем, и здесь есть недостаток, не позволяющий применить данный метод для крупных и опасных производств. Все факторы, которые берутся в расчёт, имеют одинаковый вес, подразумевая, что каждая опасность равнозначна остальным.
А вот Вам пара советов, как НЕ нужно проводить оценку профессиональных рисков
Балльные методы оценки профессиональных рисков
Эти методы задействуют специальную балльную систему (от 1 до 6): чем выше балл, тем меньше соответствуют условия труда действующим нормам и правилам. В расчёте показателя уровня риска участвуют результаты проведения специальной оценки условий труда. Главный плюс данного метода в том, что имеется возможность соотнести профессиональные риски в конкретном подразделении, организации в целом, или сравнить несколько организаций.
Новости
Оценка профессиональных рисков. Матричный метод
В настоящее время можно выделить около 70 разных методов проведения оценки профессиональных рисков. Тем не менее, нет единого установленного метода, который мог бы использоваться организациями для оценки. Данный вопрос можно решить путем применения матричного способа оценки профессиональных рисков.
Матричную методику можно определить как метод, основанный на расчете вероятности возникновения опасных ситуаций и уровне тяжести последствий для безопасности и здоровья сотрудника.
Ключевыми задачами оценки профессиональных рисков с использованием матричного метода является:
Следующий этап — оценка профессиональных рисков с учетом тяжести и вероятности возникновения:
На основе анализа травматизма с учетом тяжести и вероятности возникновения необходимо провести оценку профессиональных рисков и сформулировать возможные решения по устранению возможной опасности:
Анализ травматизма:
Решения по устранению опасностей:
Матричную оценку рекомендовано проводить каждый месяц для каждого отдельного подразделения организации. При проведении расчета перечисленных коэффициентов вероятность рисков может быть снижена к нулю. Так же с помощью данной оценки можно определить слабые места каждой структуры, где работник подвержен риску получить производственную травму.
«Матрица рисков» компании. Алгебраическое исследование
Мне доводилось принимать участие в упражнениях с Матрицей рисков компании.
Действие происходило в три этапа. Первый: мальчики и девочки анкетировали вопросами типа «перестал ли ты пить коньяк по утрам», на которые надо отвечать только «да» или «нет».
На втором этапе показывалась «научно-обоснованная» матрица рисков.
На перманентном третьем этапе все подразделения той компании пытались из года в год сдвинуться на более низкие позиции на матрице, но это удавалось только за счет личного обаяния. Те же, кто не смог сдвинуться становились крайними по любой неудаче бизнеса.
1. Матрица рисков: удобно заполнять, не удобно работать.
Вот типовая Матрица рисков, которую предлагает Google.
Для примера в Интернете найдена случайная Матрица рисков из очень старого отчета.
Числа внутри цветных прямоугольников означают содержательную интерпретацию риска, которая пока не очень нужна. Описание риска очень широко и размыто. Не верится, что все компоненты описания по отдельности и вместе дают единственное число в очень узком диапазоне.
Если следовать типовой матрицы Google, то всем содержательным описаниям «вероятность» и «влияние» можно поставить в соответствие конкретные числа.
Вот шаблон модернизированной матрицы Google с умноженными вероятностями, соответствующие горизонтальному и вертикальному шкалированию.
Она не очень удобна для применения стандартных матричных операций, так как симметрична относительно дополнительной, а не главной диагонали.
Возможно, что Матрица рисков в такой форме более удобна для менеджеров. Её перестройка с симметрией относительно главной диагонали не меняет сути матрицы. Кроме того, всегда можно сделать шаг назад и вернуться к исходному представлению.
Перестроение матрицы происходит путём замены порядка строк на обратный (симметрия относительно вертикальной центральной оси). В результате получена матрица симметричную относительно главной диагонали.
Эти же преобразования для исследуемой Матрицы рисков.
Числа, отличные от 0 — это номер риска, связанный в итоге с неким структурным подразделением. Эта кодировка имеет место только в связи с бюрократической иерархией в компании, а не с рисками. Например, для элемента <1,5>. В плане риска ситуация ничем не будет отличаться, если совместить описания риска1 и риска5. Если это разные риски, то можно уменьшить шаг матрицы и поместить риск в более подходящую позицию.
В итоге преобразования должны приводить к тому, что каждый различный риск является отдельным элементом.
Позиция [1,3] в стандартной системе нумерации матриц означает элемент, находящийся на пересечении 1-ой строки и 3-го столбца. Для рассматриваемой матрицы в позиции [1,3] стоит число 2. Это означает, что если имеет место шкала с максимальным значением «5 — почти произошло» (1.), то в [1,3] ожидаем «3 — среднее» (0.6) влияние. Пусть «влиянию» в шкалируемом промежутке соответствует определенный ущерб (damage): 5-d5, 4-d4, 3-d3, 2-d2,1-d1. Тогда, если за определенный период имело место 1 происшествие из группы 2, то ущерб составит 1.*0.6*d3*1, а если за этот же период произошло n происшествий из группы 2, то ущерб составит 1.*0.6*d3*n
Тогда исследуемая матрица примет вид.
Проводится еще одно преобразование: транспонирование путём перемены мест столбцов и строк.
Нижняя строка легенды становится излишней, так как соответствующая вероятность учтена в значениях матрицы. Первый вертикальный столбец также учтен в значениях матрицы, но он важен тем, что задает структуру событий, которые можно фиксировать или прогнозировать за некий период. Имея вектор-столбец из количества событий, относящихся к соответствующему типу (очень сильное, критическое,…) можно стандартным образом умножать матрицу на вектор-столбец и получать структурированный размер ущерба.
Без легенды матрица будет выглядеть так.
2. Матрица рисков: удобно вычислять, не удобно анализировать.
Первая основная задача.
Получив матрицу А можно приступать к решению первой основной задачи: при известном количестве и качестве произошедших событий вычислить размер ущерба.
Пусть за определенный период произошло 2 — «очень сильных» событий, 3 — «критичных», 1 — «среднее», 5 — «минимальных» и 7 — «незначительных». Умножив матрицу А на вектор количества событий получаем структуру ущерба.
Теперь можно проверять точность оценок, вносить коррективы, оценивать возможные варианты сокращения размера ущерба.
Приведенные трансформации исходной матрицы были проведены, чтобы получить простую вычислительную процедуру ущерба. От матрицы А всегда можно однозначно вернуться к исходной матрице.
3. Матрица рисков: какая теория за ней стоит?
Для любой невырожденной квадратной матрицы имеется однозначное линейное преобразование, соответствующее этой матрице. При обозрении матрицы сложно понять какое линейное преобразование стоит за ней. Кроме того, неизвестно в каком базисе произведено матричное представление.
Матрица риска — квадратная матрица и ей должно соответствовать некое линейное преобразование. Этот факт не зависит от способа получения матрицы и идей реализованных в конкретном способе получения матрицы.
Важно, чтобы определитель матрицы не равнялся нулю. Это требования метода, обеспечивающего каноническое представление матрицы.
Далее показывается, что это не просто ограничение метода, а требование отвечающее потребностям практики.
Рассматриваемая Матрица рисков имеет две нулевых строки и один нулевой столбец. В любом случае определитель этой матрицы будет равняться нулю. Ниже приведен рисунок, показывающий как компания намерена снижать риски.
Стрелками показано как будут снижаться риски. Каким образом — не важно, важно, что при этом новая ситуация опять представляется матрицей. Этой матрице соответствует некое линейное преобразование. Переход от «старой» матрицы к «новой» — это матрица и линейное преобразование.
Что означает ненулевой определитель? Это возможность шагать «вперед-назад». Если определитель нулевой, то шага «назад» сделать нельзя.
При этом матрица снижения рисков изначально связана со «старой» матрицей. То есть на картинке можно и нужно парить «вперед-назад», а в формализованном варианте шагать «вперед-назад» нельзя.
Следующая проблема связана с тем, что большой риск с малой вероятностью может быть сопоставим с риском от очень большого количества малых рисков с малой вероятностью.
В приведенном выше примере 7 незначительных событий формально не вызывают ни какого ущерба. Понятно, что это не так. Отсутствие малых рисков только подчеркивают недостаточную некорректность формирования Матрицы рисков.
Пусть определитель Матрицы рисков не равен нулю и это следствие преемственности работ по снижению рисков, а не искусственное для бизнеса требование математического метода.
Итак, имеются:
— Матрица рисков, которая соответствует неизвестному линейному преобразованию и неизвестному базису;
— определитель Матрицы, который не равен нулю.
Что можно сделать? Привести Матрицу рисков к каноническому виду с понятным ортонормированным базисом.
В работе Александра Емелина дается следующее аллегорическое описание преимуществ канонического вида. “Предположим, что есть листок бумаги, на котором написано некоторое слово. Но он сложен так, что слова не видно. После канонического преобразования листок разворачивается таким образом, что слово можно увидеть. Если используется ортонормированный базис, то листок бумаги останется того же размера.”
Никакие приведенные в работе операции и трансформации не меняют существа явлений, отраженных и содержащихся в Матрице рисков.
4. Матрица рисков как алгебраическая конструкция.
Вторая основная задача. Каноническое представление.
В рассматриваемую матрицу добавляются элементы так, чтобы определитель не равнялся нулю. Чтобы избежать слишком больших формул значения округляются.
Далее по стандартной схеме матрица приводится к каноническому виду.
Собственные значения Матрицы рисков.
Дальнейшая работа с символическими значениями будет тяжёлой при ортогонализации и результат будет невозможно визуализировать (очень громоздкие символические матрицы).
Пусть (для примера) d1=1, d2=2, d3=5, d4=8, d5=12.
Тогда Матрица рисков М в симметрическом представлении принимает вид.
Проверяется, что определитель М не равен нулю.
Вычисляются собственные значения.
Находится матрица из собственных векторов.
Она ортогонализируется. Получается матрица ORT ортонормированных векторов.
Для проверки первый вектор (столбец) умножается попарно на все остальные. Значения ненулевые, но близки к 0.
В новом базисе находится представление исходного линейного преобразования (определяющего Матрицу рисков) в переменных z1, z2, z3, z4, z5.
Если пренебречь очень маленькими слагаемыми, то получается каноническое представление линейного преобразования.
Причем коэффициенты при квадратах соответствуют ранее вычисленным собственным значением.
Новый вид Матрицы рисков в ортонормированном базисе.
Получается знакопеременная квадратичная форма.
5. Практическая польза канонического представления.
Что можно сказать про исходную Матрицу рисков?
Она представляет неизвестное линейное преобразование.
Её строки обозначаются (сверху-вниз) как x1, x2, x3, x4, x5. Строки Матрицы рисков представляют разложение по неизвестному базису.
Так
x1=10*d5*b1+0*b2+0*b3+0*b4+0*b5,
x2= 8*d4*b1+0*b2+4*d4*b3+0*b4+0*b5, и так далее.
Наличие ортонормированного базиса обеспечивает свободу хождения между переменными X и Z.
В переменных Z явно видна функция линейного преобразования в ортонормированном базисе. Поведение этого же линейного преобразования в исходной Матрице рисков было непонятным.
Явная польза от канонического вида состоит в возможности корректировки шкалирования для разных типов событий (происшествий). Если изначально шкалирование событий (очень сильное, критическое,…) шло по шагу в 20%, то теперь его можно пересмотреть, пересчитав значения концов диапазонов в новом базисе. Останется так же 5 типов событий (происшествий), но шаги между ними будут разными.
6. Матрица рисков: квадратичная форма определяет содержание.
Описанная практическая польза может показаться смешной на фоне сделанных перед этим не совсем простых манипуляций: «овчинка не стоит выделки».
Ясная, понятная и простая форма Матрицы рисков Google не совсем соответствует содержанию работе с рисками.
Что такое риск: рассчитываешь на одно, а по факту получаешь другое.
Матрица рисков Google сделана так, что компания всегда однозначно знает свои риски и последовательно работает над их снижением. Более того, все высокие риски с большим ущербом постепенно ликвидируются. Слава мудрым менеджерам.
Напротив, полученная в ортонормированном базисе Матрица рисков будет всегда показывать наличие непустых высоких рисков.
Сформированное в 4 разделе каноническое представление можно интерпретировать как ущерб, который получается, когда происходят те события, которые ожидаются: переменная в квадрате.
Есть еще одно немаловажное обстоятельство. Ущерб имеет место так же в том случае, если произведены затраты для предотвращения ситуаций, которые никак не происходят.
Следующая новая конструкцию.
Значения v[i,j] соответствуют ущербу (выгоде) при условии, что рассчитывали на событие f(j), а реально произошло событие f(i). Значения v[i,j] могут быть как положительными (ущерб), так и отрицательными (выгода).
Значение v[i,i] соответствует ситуации, когда фактически произошло то событие, к которому готовились: на что рассчитывали, то и получили.
В этом случае Матрица рисков принимает вид.
Вектор-столбец событий имеет вид.
При этом размер ущерба описывается квадратичной формой.
Приведенную новую конструкцию описания рисков можно связать со следующими вычислениями: оценка ущерба при фактическом наступлении события f(i), тогда как мероприятия ориентированы на событие f(j).
Тогда проясняется какие «мероприятия по снижению рисков» требуются:
— для тех рисков, к которым не готовились, но они часто проявляются;
— для рисков, выделенных как базовые.
Кроме того, все алгебраические манипуляции описанные выше становятся не просто уместными, а обязательными.
Задача минимизации рисков сводится к минимизации значения ущерба, задаваемого каноническим представлением квадратичной формы ущерба.
7. Матрица рисков как инструмент цифрового управления.
В общем случае можно использовать разные методы оценки и управления рисками: имитационное моделирование, системы массового обслуживания, оценку устойчивости структурных схем последовательно-параллельного соединения компонентов и другие.
В данном случае рассматривается «жанр» Матриц риска и его возможности для улучшения бизнеса.
Фактически новая форма позволяет Матрице рисков уйти от роли «жупела» и стать нормальным инструментом цифрового управления бизнесом. Одним из многих для современного бизнеса.
Для этого необходимо поменять методику исчисления ущерба, сделав упор на проверяемые количественные значения по сравнению с ориентацией на качественные экспертные оценки.
Матрица оценки профессиональных рисков по трехуровневой шкале
В 2021 году запланированы глобальные изменения в законодательстве по охране труда. В Трудовом Кодексе РФ переработан 10 раздел «Охрана труда». Одно из изменений 10 раздела Трудового Кодекса РФ коснулось необходимости проведения, в обязательном порядке, оценки профессиональных рисков. В свете новых изменений, радует тот факт, что Государство не будет настаивать на использовании методики, разработанной Минтрудом РФ. Работодатель может использовать приемлемую для себя методику оценки рисков. Таким образом, не потребуется пересматривать оценку рисков предприятиям, где эта система внедрена и работает.
До 2021 года оценка профессиональных рисков не входила в перечень обязательных мероприятий для исполнения работодателями, но компании крупного бизнеса, по собственной инициативе, давно проводят оценку рисков. Так как задача менеджмента любого предприятия — управление деятельностью, продукцией и услугами с целью устранения неприемлемых рисков или снижения их до приемлемого уровня.
С 2022 года Оценка профессиональных рисков перестаёт быть чем-то аморфным и не обязательным. С 01.03.2022 года риски станут неотъемлемой составляющей жизни каждой организации.
В настоящее время используются различные методики для оценки рисков, все они основываются на перемножении ключевых показателей вероятности возникновения риска и его последствий (потери здоровья и материальных потерь). Матрица рисков может состоять из трех, пяти и более многоуровневой шкалы. Метод оценки рисков с многоуровневой шкалой, например, разработан для американского военно-морского флота. Основная формула:
Р = (Вч + Вк +Во) х П х Вр, где
Идентификация опасностей, связанных с различными видами деятельность (опасность-это источник или ситуация, которая потенциально может привести к ухудшению здоровья, нанесению ущерба собственности, ухудшит окружающую среду рабочего места или сочетание всего этого);
Оценка уровня риска, связанного с выявленной опасностью (риск-сочетание вероятности и последствий конкретного возникающего случая)
Предлагаю для работы простую и удобную в работе методику оценки рисков, по которой оценены риски для:
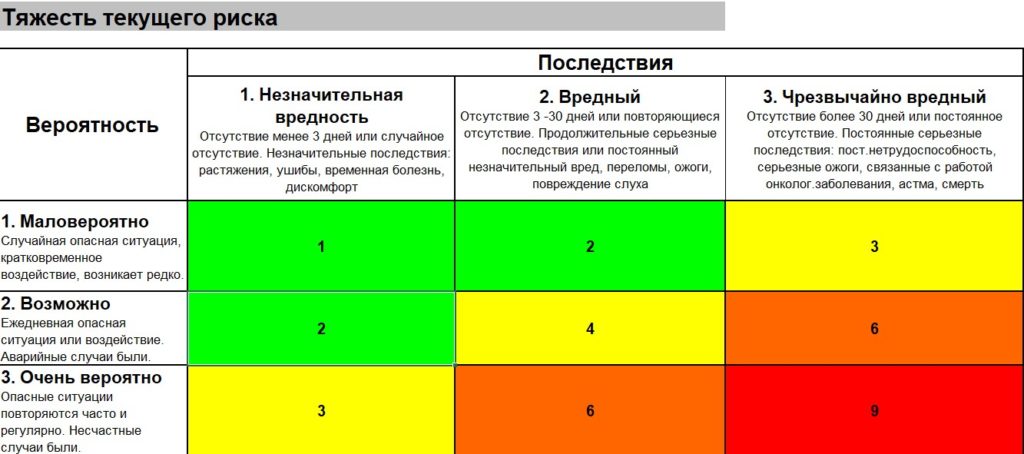
По данной методике оценки в матрице рисков для каждой опасности вероятность ее возникновения и последствия определены по 3-х уровневой шкале (3х3). Перемножив вероятность и последствия, мы получаем величину тяжести текущего риска.
1. Вероятность риска оценивается по следующей шкале:
2. Последствия риска оцениваются по следующей шкале:
Как можно увидеть из таблицы, наиболее значительный риск на уровне девяти, а наименьший риск равен единице.
О матричных методах оценки рисков по 3-х уровневой и 5-и уровневой шкале рассказывает эксперт.
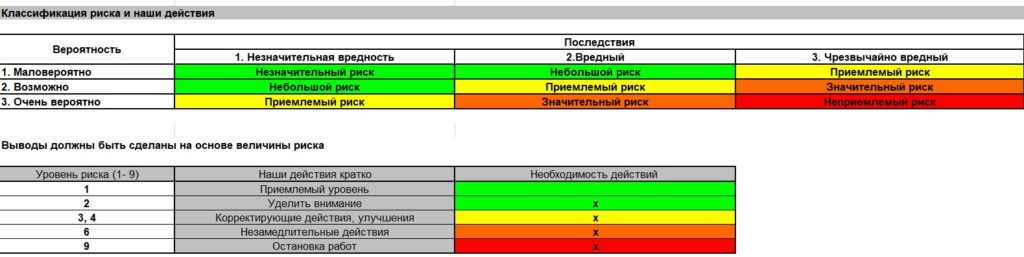
После идентификации риска, для его исключения или снижения, следует разработать комплекс мероприятий. Необходимость проведения мероприятий напрямую зависит от тяжести риска. Специальное внимание должно быть уделено контролю наиболее тяжелым рискам, когда уровень риска равен 6 или 9. Анализ по предотвращению таких ситуаций должен быть более глубоким и тщательным, чем при обычной оценке. Также потребуется более тщательное планирование и внедрение мероприятий.
При повышенном уровне риска, когда уровень риска равен 3 или 4, мероприятия должны быть не такие срочные как при уровне 9, но сокращение риска проводить нужно обязательно. Мероприятия могут быть направлены на уменьшение вероятности возникновения опасной ситуации или на сокращение воздействия от неё.
На уровне 1 никаких мероприятий не требуется. Тем не менее, так как опасность существует, ее необходимо постоянно отслеживать и проводить переоценку.
| Риск | Действия |
| (1) Незначитель-ный риск | Дополнительные мероприятия или дополнительный контроль не требуется |
| (2 ) Небольшой риск | Риск находится (или был сокращен) на таком низком уровне, какой наиболее применим на практике. Дополнительные мероприятия не требуются. Рассмотрение может быть при более эффективном, с точки зрения затрат, решении или улучшении, которое не требует денежных затрат. |
| (3-4) Приемле-мый риск | Мероприятия должны быть произведены для снижения риска, но затраты по улучшению должны быть тщательно оценены и ограничены. Мероприятия по снижению риска должны быть четко ограничены по времени. В местах, где умеренный риск ассоциируется с особо вредными условиями, должны быть внедрены дополнительные мероприятия и они должны отслеживаться. |
| (6) Значитель-ный риск | Работа не должна продолжаться, пока риск не сокращен. Значительные средства могут быть потрачены для сокращения риска. Если риск входит в обычную работу, срочные мероприятия должны быть внедрены незамедлительно. |
| (9) Неприем-лемый риск | Работа не должна начинаться или продолжаться, пока риск не сокращен. Если невозможно сократить риск даже с привлечением огромных ресурсов, работа все равно должна быть прекращена. |
Мероприятия, направленные на снижение риска должны следовать следующей иерархии:
Задача менеджмента — управление деятельностью, продукцией и услугами с целью устранения неприемлемых рисков или снижения их до приемлемого уровня.