Что такое звездный параллакс
Звездные параллаксы
До XVI в. ученые не особо стремились измерять расстояния до звезд, поскольку были уверены: абсолютно все светила — это что-то вроде украшения небесного купола, а так как Земля занимает центральное место во Вселенной, то звезды удалены от нее одинаково. К тому же путь до них слишком дальний— обычными приборами его не измеришь… Разумеется, подобные суждения были ошибочными, ив 1584 г. об этом впервые заявит итальянский ученый-философ Джордано Бруно (1548—1600). Из его труда «О бесконечности. Вселенной и мирах» люди наконец узнали о том, что никакого небесного купола не существует, космос не имеет ни конца ни края, а звезды — подобные Солнцу тела со своими системами планет, расположенные на разных расстояниях от Земли.
Идея объемного, трехмерного космического пространства не сразу нашла отклик в умах консервативных ученых, но все же подтолкнула их к размышлениям о том. как определить, насколько удалена от нас та или иная звезда. И физики, и астрономы бились над этой задачей вплоть до XIX в., но впустую.
В 1572 г. датский ученый Тихо Браге (1546—1601) впервые попытался определить путь от Земли до звезд методом параллакса— то есть зарисовать положение светила на небе в разное время, а затем измерить углы между этими позициями и позицией наблюдателя. Ученый исследовал таким образом 777 светил, но, очевидно, промахнулся с интервалом между замерами для каждой звезды и потому никаких параллаксов не обнаружил. Из этого он заключил: Земля неподвижна, а Коперник со своей гелиоцентрической системой явно что-то напутал. И вообще, разве могут звезды быть настолько далеки и настолько огромны?!
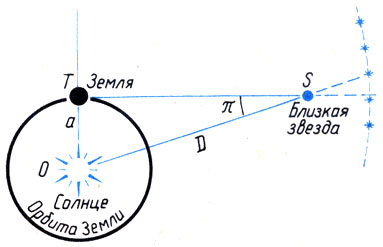
Между тем метод, использованный Браге, был очень эффективным. Если посмотреть на любой предмет сначала одним, а потом другим глазом, мы увидим, что наш объект находится немного в разных местах. Так же и со звездами. Но тут имеет смысл делать измерения раз в полгода — тогда получится, будто мы смотрим на звезду с противоположных сторон земного шара. Визуально светило значительно сместится на небосводе, так что мы сможем измерить угол между собой и двумя звездными положениями, идентичный тому углу, под которым со звезды виден весь диаметр земной орбиты. Чтобы узнать, под каким углом со светила видно радиус этой орбиты — то есть расстояние от нашей планеты до Солнца. — нужно разделить первый угол надвое, и получится тот самый параллакс. По нему вычислить расстояние до звезды уже не сложно, однако в XVI в. об этом попросту не знали…
Примерно через два столетия проблемой удаленности звезд занялся британский астроном Джеймс Брэдли (1692—1762). которому суждено было в будущем возглавить обсерваторию Гринвича. В качестве объекта наблюдений он выбрал звезду Гамма Дракона и целый год следил за ней. исправно зарисовывая смены ее расположения. В итоге оказалось, что звезда постоянно смещается влево-вправо на 20 секунд, однако эта цифра оказалась стишком большой для параллакса. Эксперимент не удался, зато Брэдли сделал вывод, что «неусидчивость» звезды вызвана наложением скорости, с которой распространяется ее свет, на скорость вращения Земли. А значит. Земля таки вертится вокруг Солнца.
Понадобилось еще 100 лет. чтобы усовершенствовать измерительные приборы, а затем повторить попытку. В конце 1830-х расстояния до звезд решили измерить одновременно трое ученых. Одним из них был русский геодезист и астроном Василий Струве (1793—1864). наблюдавший за самой яркой звездой созвездия Лиры — Вегой. Как и следовало. Струве зафиксировал положения Беги с промежутком в полгода и определил, что ее смещение составило четверть секунды, то есть радиус земной орбиты (дистанция между Землей и Солнцем) просматривается со светила под углом 0.125″, а параллакс равен десятимиллионной части окружности. По расчетам ученого, такой параллакс соответствовал расстоянию в 250 трлн км, или 26.5 светового года (1 световой год— путь, пройденный лучом света за год,— равен 9.5 трлн км). Это было громадное расстояние: обычный самолет преодолел бы его не менее чем за 40 млн лет (если бы. конечно, мог летать в космосе).
По примеру Струве немецкий астроном Фридрих Бессель проследил смещения 61-й звезды Лебедя, которая двигается по небосводу быстрее остальных светил. Чтобы определить параллакс звезды — 0,3 секунды — и расстояние до нее (около 11 световых лет), ученому пришлось провести около четырех сотен измерений. Но на этом он не остановился и измерил удаленность еще 50 000 звезд. Между тем в 1839 г. были обнародованы результаты работы шотландца Томаса Хендерсона. исследовавшего в Южной Африке самую близкую к экватору систему Альфа Центавра. Правда, величина найденного им параллакса (1,16 секунды) оказалась в 1.5 раза выше, чем на самом деле; да и вообще, дальнейшие измерения показали, что угол обзора радиуса земной орбиты со звезды не может превышать 1 секунды.
СОДЕРЖАНИЕ
Параллакс метод
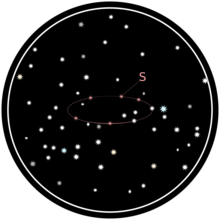
В течение года отмечается положение звезды S по отношению к другим звездам в ее видимом окружении:
Звезды, которые, казалось, не двигались относительно друг друга, используются в качестве ориентиров для определения пути S.
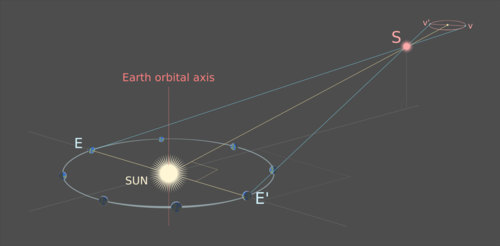
Наблюдаемый путь представляет собой эллипс: проекцию орбиты Земли вокруг Солнца через точку S на далекий фон неподвижных звезд. Чем дальше S удаляется от оси орбиты Земли, тем больше эксцентриситет траектории S. Центр эллипса соответствует точке, в которой S будет видна с Солнца:
Плоскость орбиты Земли находится под углом к линии, идущей от Солнца через S. Вершины v и v ‘эллиптической проекции траектории S являются проекциями положений Земли E и E’, так что линия EE ‘пересекает линия Солнце-С под прямым углом; Треугольник, образованный точками E, E ‘и S, представляет собой равнобедренный треугольник с линией Солнце-S в качестве оси симметрии.
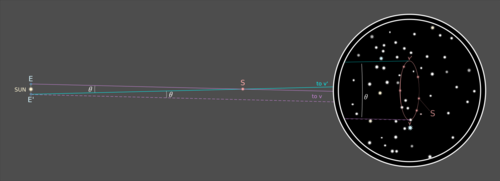
Любые звезды, которые не двигались между наблюдениями, для точности измерения находятся бесконечно далеко. Это означает, что расстояние движения Земли по сравнению с расстоянием до этих бесконечно далеких звезд в пределах точности измерения равно 0. Таким образом, луч зрения от первого положения Земли E до вершины v будет практически таким же. как луч обзора от второй позиции Земли E ‘к той же вершине v и, следовательно, будет проходить параллельно ей, что невозможно убедительно изобразить на изображении ограниченного размера:
Поскольку прямая E’-v ‘является трансверсалью в той же (приблизительно евклидовой) плоскости, что и параллельные прямые Ev и E’-v, из этого следует, что соответствующие углы пересечения этих параллельных прямых с этой трансверсалью совпадают: угол θ между линии зрения Ev и E’-v ‘равны углу θ между E’-v и E’-v’, который представляет собой угол θ между наблюдаемыми положениями S по отношению к его, по-видимому, неподвижному звездному окружению.
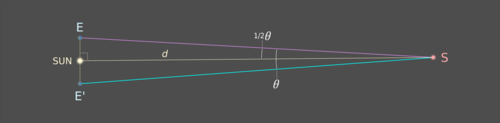
Расстояние d от Солнца до S теперь следует из простой тригонометрии:
так что d = E-Sun / tan (½θ), где E-Sun равно 1 AU.
Чем дальше объект, тем меньше его параллакс.
Ранняя теория и попытки
19 и 20 века
Звездный параллакс остается стандартом для калибровки других методов измерения (см. Лестница космических расстояний ). Для точных расчетов расстояния на основе звездного параллакса требуется измерение расстояния от Земли до Солнца, которое теперь известно с исключительной точностью на основе отражения радара от поверхностей планет.
Большой гелиометр был установлен в обсерватории Каффнера (Вена) в 1896 году и использовался для измерения расстояний до других звезд по тригонометрическому параллаксу. К 1910 году он вычислил 16 параллаксных расстояний до других звезд из всего 108, известных науке в то время.
Космическая астрометрия по параллаксу
Телескоп Хаббла WFC3 теперь имеет точность от 20 до 40 микросекунд, что позволяет надежно измерять расстояние до 3066 парсек (10 000 световых лет) для небольшого числа звезд. Это придает большую точность космической лестнице расстояний и улучшает знание расстояний во Вселенной на основе размеров орбиты Земли.
По мере увеличения расстояния между двумя точками наблюдения визуальный эффект параллакса также становится более заметным. NASA «s New Horizons космический корабль совершил первый межзвездный измерения параллакса на 22 апреля 2010, принимая образы Проксима Центавра и Волк 359 в сочетании с наземных обсерваторий. Относительная близость двух звезд в сочетании с расстоянием 6,5 миллиардов километров космического корабля от Земли дала заметный параллакс в угловые минуты, что позволило увидеть параллакс визуально без использования приборов.
Радиоастрометрия для параллакса
Интерферометрия с очень длинной базой в радиодиапазоне может давать изображения с угловым разрешением около 1 миллисекунды, и, следовательно, для ярких радиоисточников точность измерений параллакса, сделанных в радио, может легко превзойти точность оптических телескопов, таких как Gaia. Эти измерения имеют тенденцию быть ограниченными по чувствительности и должны выполняться по одному, поэтому работа обычно выполняется только для таких источников, как пульсары и рентгеновские двойные системы, где радиоизлучение является сильным по сравнению с оптическим излучением.
Прочие исходные данные
Статистический параллакс
Два связанных метода позволяют определять средние расстояния до звезд путем моделирования движения звезд. Оба называются статистическими параллаксами, или отдельные, называемые вековыми параллаксами и классическими статистическими параллаксами.
Движение Солнца в космосе обеспечивает более длинную базовую линию, которая увеличивает точность измерений параллакса, известного как вековой параллакс. Для звезд в диске Млечного Пути это соответствует средней базовой линии 4 а.е. в год, тогда как для звезд с гало базовая линия составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на несколько порядков больше, чем базовая линия Земля – Солнце, используемая для традиционного параллакса. Однако вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость других звезд является дополнительной неизвестной. Применительно к выборкам из нескольких звезд неопределенность может быть уменьшена; точность обратно пропорциональна квадратному корню из размера выборки.
Другой параллакс в астрономии
Параллакс

Краткие сведения
Радиус земной орбиты составляет одну астрономическую единицу или около 150 миллионов километров. В связи с этим все внеземные объекты на земном небе так же выписывают годичные “петли” (параллактическое движение). Чем дальше небесный объект находится от Земли, тем его параллактическое движение на земном небе является менее заметным (в переводе с греческого слово “параллакс” означает “смещение”).
Измерения углового диаметра параллактического движения небесных тел на земном небе позволяет проводить наиболее точные измерения расстояния до них (тригонометрическое расстояние). Кроме того, важным в истории астрономии оказался суточный (геоцентрический) и вековой параллакс. Первый из них обозначает половину от максимального различия в угловых координатах небесного тела на земном небе при различных географических положениях на поверхности Земли (относительно центра Земли), второй обозначает собственные движения звезд на небе нашей планеты по причине движения Солнечной Системы вокруг центра галактики.
История
Суточным (геоцентрическим) параллаксом называется угол, под которым виден земной радиус с определенного небесного тела. Кроме того, выделяют понятие горизонтального параллакса. Горизонтальным параллаксом называется угол, под которым виден экваториальный радиус Земли из центра определенного небесного тела при нахождении последнего на истинном горизонте (истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения). Различия понятий суточного и горизонтального параллакса связаны с несферичностью Земли (так полярный радиус Земли короче экваториального радиуса на 21 км).
Суточный параллакс сыграл очень важную роль в истории астрономии, как наиболее простой и достоверный способ определения расстояния до объектов Солнечной Системы. Фактически этот метод являлся единственным геометрическим методом измерения расстояний в Солнечной Системе вплоть до радиолокации, лазерной локации и методов радиоинтерференции сигналов межпланетных станций. Базой суточного параллакса является земной радиус. Самым большим суточный параллакс является у Луны (57 угловых минут) и у Солнца (9 угловых минут). У всех планет Солнечной Системы суточный параллакс подвержен регулярным изменениям и значительно меньше угловой минуты (у Венеры 0.1-0.6 угловых минут, у Марса 0.1-0.4 угловых минут, у Юпитера и Сатурна меньше 0.1 угловой минуты, а у Урана и Нептуна меньше одной угловой секунды).
Первыми параллакс Луны и Солнца определили древнегреческие астрономы на основе наблюдений лунных затмений, которые позволяли определять параллакс Луны из одного и того же места. Так древнегреческий астроном Гиппарх Никейский (180-125 годы до нашей эры) в 129 году до нашей эры оценил параллакс Солнца в 7 угловых минут (максимальная величина угла, который неразличим невооруженным глазом). Похожие расчеты выполнил до него другой древнегреческий астроном Аристарх Самосский (310-230 годы до нашей эры).
С другой стороны, александрийский астроном Клавдий Птолемей (100-170 годы нашей эры) полагал, что расстояние до Луны зависит от её фаз. Это говорит о больших разногласиях среди астрономов Древнего мира по поводу оценок параллаксов Луны и Солнца. Позже ошибка Птолемея о зависимости размера параллакса Луны от её фаз стала одним из основных объектом критики птолемевской системы мира. Так юный Николай Коперник (1473-1543 годы нашей эры) во время учебы в Италии проводил измерения параллакса Луны вместе со своим учителем Новарой. Наблюдения положения Луны во время затмения яркой звезды Альдебаран из Болоньи 9 марта 1497 года показали, что параллакс Луны не зависит от её фазы. В последующие века началось широкое использование одновременных наблюдений из северного и южного полушария для точного измерения параллаксов Луны, Солнца и Марса. К примеру, в 18 веке такие наблюдения осуществлялись в обсерватории мыса Доброй Надежды в южной части Африки и Берлинской обсерватории.
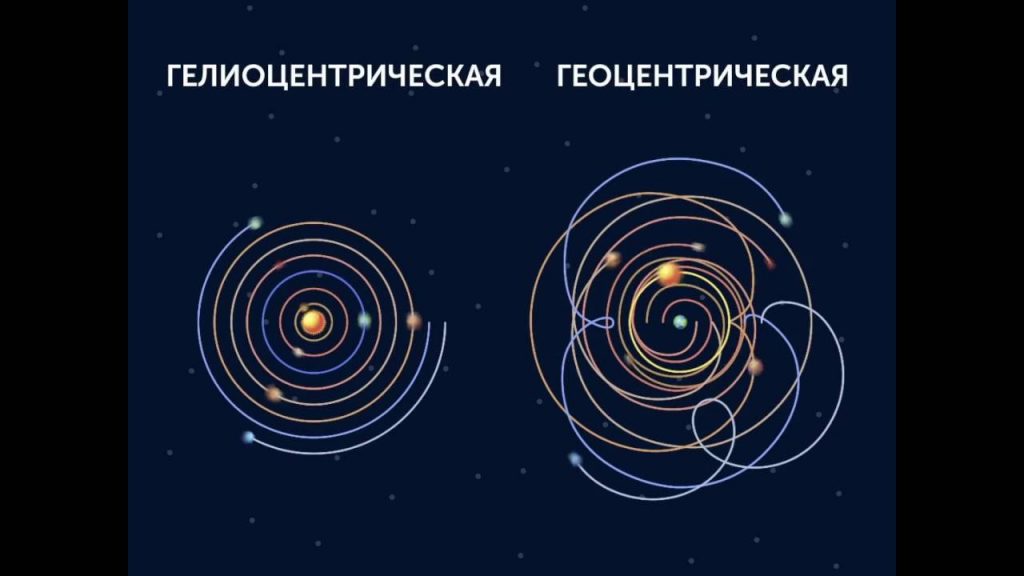
Сравнение гелиоцентрической и геоцентрической системы мира
Сравнение гелиоцентрической и геоцентрической системы мира
Годичный параллакс (звездный параллакс) даже у ближайших звезд не превышает одной угловой секунды. В связи с этим его измерение стало возможным лишь после изобретения оптических инструментов – телескопов. Сама возможность существования этого явления стала причиной принципиальных разногласий между геоцентрической и гелиоцентрической системами мира – геоцентрическая система считала, что Солнце обращается вокруг Земли. В то же время сторонники гелиоцентрической системы в течение почти 2 тысяч лет объясняли ненаблюдаемость звездных параллаксов огромными расстояниями до звезд. Первые попытки измерения звездных параллаксов были предприняты древнегреческим астрономом Аристархом Самосским в 3-ем веке нашей эры (считается, что он первым выдвинул предположения о гелиоцентрической системе мира). Позже такие попытки были предприняты Н. Коперником, Т. Браге, Г. Галилео, У. Гершелем и т.д. Последний во время попыток обнаружения звездных параллаксов случайно открыл неизвестную планету Солнечной Системы – Уран. По иронии судьбы, к тому времени, когда в начале 19 века всё же удалось измерить первые параллаксы звезды, сомнений в справедливости гелиоцентрической системы мира уже не оставалось. Так в ходе безуспешных попыток измерить параллакс у звезды Гамма Дракона (Этамин) английский астроном Джеймс Бредли (1692-1762 годы) в 1727 году открыл явление аберрации света, которая вызвана орбитальным движением Земли вокруг Солнца. Аберрация света представляет собой изменение видимого положения звезд примерно на 50 угловых секунд по причине конечной скорости света (первооткрыватель годичной аберрация определил скорость света в 308 тысяч км в секунду). Одновременно Д.Бредли получил верхний предел для звездных параллаксов в 0.5 угловой секунды. С другой стороны в попытках измерить звездные параллаксы, другому английскому астроному Уильяму Гершелю (1738-1822 году) в 1803 году удалось впервые зарегистрировать орбитальное движение двойных звезд (ранее предполагалось, что визуальные двойные звезды являются результатом случайности). Кроме того У. Гершель первым определил на основе наблюдаемых собственных движений звезд, что Солнечная Система движется в сторону созвездия Геркулеса.
Впервые факт отсутствия неизменности положения звезд на земном небе был обнаружен ещё Гиппархом на основе сверки положения ярких звезд его каталога, состоящего из примерно тысячи звезд с более древними каталогами вавилонян и александрийских астрономов. Гиппарх обнаружил систематическое изменение долготы положения звезд примерно на один градус (в то время как широта звезд относительно эклиптики оставалась неизвестной). Ныне это явление называется прецессией земной оси с периодом в 26 тысяч лет. Истинное движение звезд было впервые обнаружено в 1718 году английским астрономом Эдмондом Галлеем (1656-1743). В процессе уточнения прецессии Э. Галилей сравнил положения звезд из каталога Гиппарха с современными звездными каталогами. Сравнение показало, что на фоне большинства звезд, у которых положение на земном небе менялось согласно прецессии, встречался ряд аномалий (для Сириуса, Арктура и Альдебарана). У этих звезд отклонения в положении в несколько раз превысили погрешность измерений.
Василий Струве и Пулковская обсерватория в которой он работал
Первые достоверные измерения звездных параллаксов были опубликованы в 1837-1838 годах сразу тремя исследователями: Василий Струве (1793-1864 годы) для Веги, Фридрихом Бесселем (1784-1846 годы) для 61 Лебедя и Томасом Хендерсоном (1798-1844 годы) для Альфы Центавра. Хотя за много лет до этого – к 1822 году Фридрих Струве в Дерптской обсерватории на территории нынешней Эстонии получил достаточно точные измерения параллаксов нескольких ярких звезд (к примеру, для Альтаира).
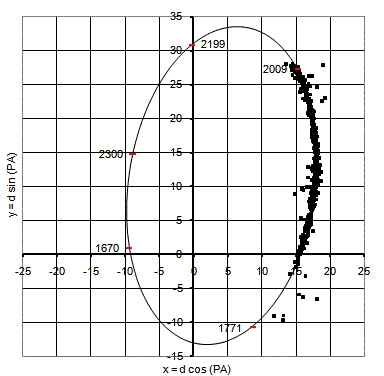
Орбитальное движение звезд системы 61 Лебедя (черным отметками отмечены измерения астрономов)
Кроме того французский астроном Доминик Араго (1786-1853) ещё за несколько лет до Ф. Бесселя опубликовал значение параллакса 61 Лебедя с большой погрешностью. Результат Ф. Бесселя был воспринят мировым сообществом как наиболее достоверный в связи с большим количеством астрометрических измерений (более 400).
Для сравнения у Ф. Струве для Веги было сделано только 17 астрометрических измерений. Кроме того работу Бесселя облегчил факт того, что двойная система 61 Лебедя обладает заметным орбитальным движением. Так можно было сравнить параллакс для обеих звезд системы.
Визуальные измерения параллаксов и собственных движений являлись крайне трудоемкими. К концу 19 века удалось измерить тригонометрические расстояния лишь до сотни звезд. Всё резко изменилось с использованием фотографии. Точность измерений выросла до 10 угловых микросекунд, а число измеряемых звезд достигло нескольких тысяч. Замена фотопластинок приборами с зарядовой связью (ПЗС-матрицами), широкое использование компьютеров для обработки данных, а также вынос телескопов за пределы атмосферы Земли позволил улучшить точность измерения положения звезд до миллионных долей угловой секунды, а размер астрометрических каталогов вырос до девятизначных цифр.
Прогресс в точности измерения положения звезд за последние 2.5 тысячи лет
Основы геометрии и тригонометрии
При вычислении лунного параллакса активно используются основы геометрии для прямоугольного треугольника. Прямоугольным треугольником называется такой треугольник, у которого один из углов равен 90 градусов.
В прямоугольном треугольнике стороны, которые образуют угол в 90 градусов, называются катетами, а сторона, лежащая напротив угла в 90 градусов гипотенузой. Сумма углов в прямоугольном треугольнике равна 180 градусов. Отсюда несложно определить, что при известном катете (радиусе Земли) и угле между гипотенузой и катетом (суточным параллаксом) гипотенуза (расстояние до небесного тела) будет равна отношению известного катета к синусу суточного параллакса.
Только в этом случае радиус Земли заменяется радиусом земной орбиты вокруг Солнца, а суточный параллакс заменяется годичным параллаксом
Синусом в прямоугольном треугольнике называют отношение катета противолежащего угла к гипотенузе.
Аналогичный принцип вычислений существует для расчетов тригонометрических расстояний до звезд.
По причине огромных расстояний до звезд (ближайшая звезда находится в 270 тысячах астрономических единиц от Солнца), для вычисления тригонометрических расстояний чаще всего используют отношение 206265 угловых секунд и измеренного годичного параллакса, который так же представлен в угловых секундах. Число 206265 означает число угловых секунд в одном радиане. Радиан – это угол, соответствующий дуге окружности, длина которой равна радиусу этой окружности.
Частные случаи использования суточного и годичного параллакса
Многие тысячи лет число известных объектов в Солнечной Системе было постоянным и было равно девяти (Земля, Луна, Солнце, Меркурий, Венера, Земля, Марс, Юпитер и Сатурн). Это постоянство нарушали лишь кометы, которые периодически появлялись во внутренних областях Солнечной Системы. В 18 веке в Солнечной Системе начались открытия новых планет и астероидов (к примеру, Урана и Цереры). Шквал новых открытий вынудил астрономов разрабатывать методики по вычислению орбит небесных тел Солнечной Системы по минимальному числу измерений. В 1801 году 24-летний немецкий математик Фридрих Гаусс (1777-1855 годы) с целью обнаружения потерянной Цереры разработал математический метод, по которому было возможно определить орбиту небесного тела на основе всего трех его наблюдений.
В то же время примерное расстояние до небесного тела в Солнечной Системе, возможно, определить лишь по двум наблюдениям. Особенно, это актуально в случае открываемых объектов за орбитой Нептуна (ТНО). У таких объектов скорость движения является минимальной по сравнению с орбитальной скоростью Земли (несколько сотен метров в секунду против 30 км в секунду). В результате этого наблюдаемое расстояние от Солнца (гелиоцентрическое расстояние) до ТНО в астрономических единицах можно определить простым соотношением 150/q, где q – это угловая скорость объекта в угловых секундах за один час.
С другой стороны в последние годы астрометрические наблюдения мигрируют из оптического диапазона в более длинноволновые диапазоны электромагнитного спектра: инфракрасные лучи и радиоволны. Первый диапазон является очень перспективным для астрометрии красных и коричневых карликов во Вселенной (наиболее распространенной популяции массивных объектов в галактике, чей максимум теплового излучения приходится на инфракрасный диапазон). Второй диапазон является уникальным во всем электромагнитном спектре по проникающей способности.
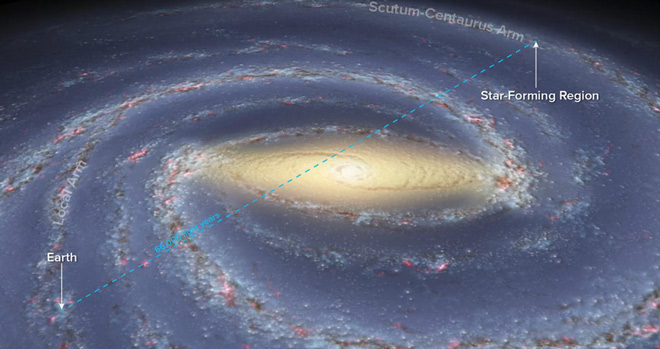
Так недавно радиоастрономы с помощью радиоинтерферометра VLBA смогли установить рекорд самого далекого измеренного параллакса: расстояние до межзвездного облака G007.47+00.05 (внешний рукав Щита – Центавра) составило 20 тысяч парсек или 67 тысяч световых лет
Вековой и внегалактический параллакс
Солнечная Система, как сотни миллиардов планетных систем нашей галактики обращается вокруг центра галактики в созвездии Стрельца. Один оборот Солнечной Системы вокруг центра галактики (галактический год) равен 225-250 миллионов лет (средняя скорость движения Солнечной Системы в межзвездном пространстве около 220 км в секунду). По причине различий в галактических орбитах другие звезды на земном небе движутся по различным траекториям, с различной угловой и пространственной скоростью.
Как говорилось выше, собственные движения звезд были впервые обнаружены в 1718 году английским астрономом Эдмондом Галлеем (1656-1743). Так как это открытие случилось за столетие до первых измерений параллаксов, звезды с высоким собственным движением стали потенциально интересными для измерения параллаксов. Из трех первых опубликованных параллаксов в 1837-1838 годах, два приходятся на звезды с высоким собственным движением (61 Лебедя и Альфа Центавра). Собственное движение этих систем составляет около 4 угловых секунд в год. Для сравнения, у третьей звезды – Веги собственное движение в 20 раз меньше (Ф. Бессель выбрал эту звезду для измерения параллакса по причине её околорекордной видимой яркости на северном небе). В дальнейшем поиск неизвестных близких звезд в большинстве случаев проходил через первоначальное обнаружение звезд с высоким собственным движением (к примеру, так были обнаружены в 20 веке звезды Проксима Центавра и Летящая Барнарда). В результате этого в последние годы астрономы открывают близкие звездные системы только с минимальным собственным движением (0.15 угловых секунд в год и меньше). Исключением из этого правила могут стать лишь плотные звездные поля или области вблизи очень ярких звезд.
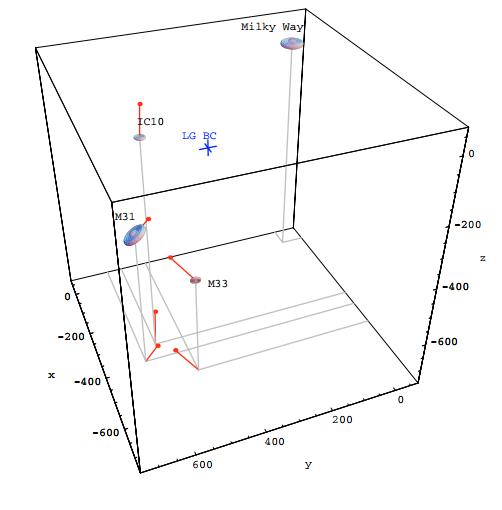
Естественно и наша галактика в космическом пространстве Вселенной не является неподвижным объектом. Сегодня астрономы полагают, что наша галактика с соседними галактиками (Местная группа галактик) входят в состав сверхскопления галактик созвездия Девы. Исследования реликтового излучения в конце 20 века показали, что Солнечная Система движется относительно реликтового излучения со скоростью 368 ± 2 км/с (или 78 астрономических единиц в год). В результате этого движения, объект, который находится в миллионе парсек от нас, и расположен перпендикулярно внегалактическому апексу будет обладать на земном небе собственным движением в 78 угловых микросекунд в год (миллионных долей угловой секунды). Подобная точность измерений является вполне достижимой в последние десятилетия. В ходе измерения собственных движений близких галактик широко используются снимки крупнейших наземных телескопов и космических телескопов Хаббл и Гаяй, а так же данные радиоинтерферометров. К примеру, измерение собственного движения галактики М31 привело к прогнозу её столкновения с нашей галактикой через несколько миллиардов лет.
Схема движения галактик в Местной группе относительно нашей галактики взята из работы A. Brunthaler et al. 2007 года
Измеренное собственное движение галактики Андромеды с расстоянием в 0.8 миллионов парсек составило около 50 угловых микросекунд в год. Для сравнения современные радиоинтерферометры способны регистрировать собственные движения галактик на основе наблюдения мазеров до удаления в 20 миллионов парсек за 10-летние наблюдения. Сложности измерения собственных движений галактик заключаются в необходимости разграничения общего движения всей галактики от орбитального движения отдельных звездных скоплений или межзвездных туманностей в ней. Решением этой проблемы является измерение собственного движения ядер галактик. В связи с этим удобным источником для измерения внегалактических собственных движений являются галактики с активными ядрами (квазары) – одни из ярчайших радиоисточников на земном небе. В работе 2005 года с названием “Quasar Apparent Proper Motion Observed by Geodetic VLBI Networks” сообщается, что геодезическим радиоинтерферометрам в период с 1980 по 2002 годы удалось измерить или ограничить собственное движение 580 квазаров.
У многих из них собственное движение составляет несколько сотен угловых микросекунд
Большинство этих источников находились на огромных расстояниях в многие миллиарды световых лет
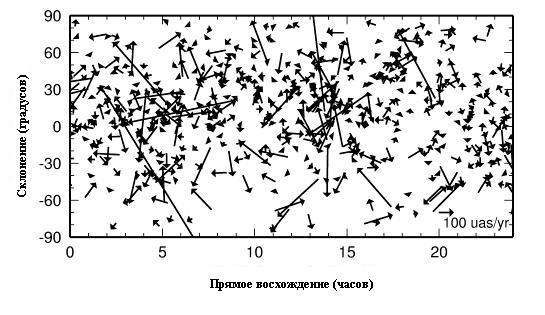
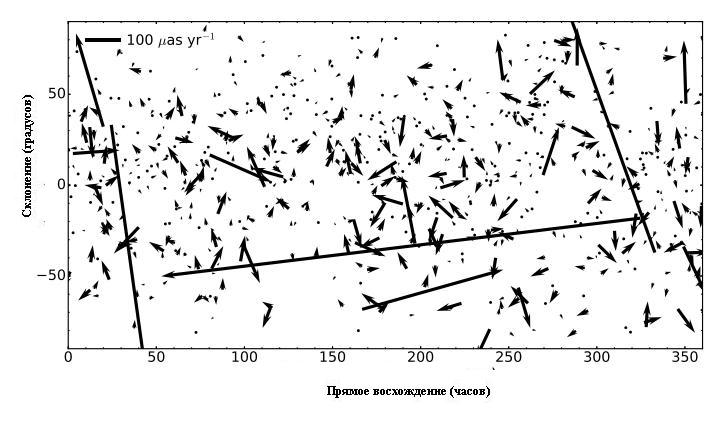
В работе 2017 года был опубликован каталог собственных движений 713 внегалактических радиоисточников, которые наблюдались в среднем около 22 лет. Средняя погрешность этих измерений составила 24 угловых микросекунд в год. Эти наблюдения позволили зарегистрировать ускорение движения Солнечной Системы по галактической орбите (статистический уровень значимости 6.3 сигм). Это явление приводит к систематическому изменению угловой скорости внегалактических объектов на несколько микросекунд в год.
Карта собственных движений из нового каталога
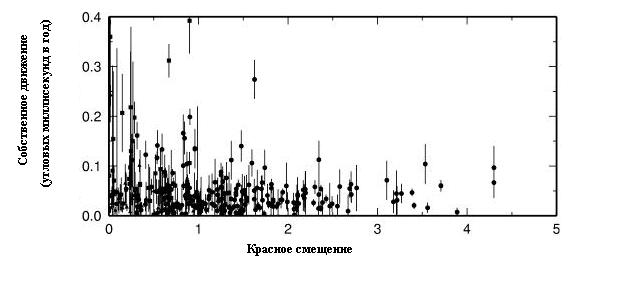
Самое большое наблюдаемое собственное движение в вышеназванном каталоге (около 1.5 угловых миллисекунд в год) наблюдается у радиогалактики SDSS J213836.38+001241.8, у которой наблюдаемый блеск в оптическом диапазоне составляет примерно 23 звездных величины (её красное смещение равно 0.6). Для сравнения у одной ближайшей галактики (Большое Магелланово облако) собственное движение равно 2 угловым миллисекундам.
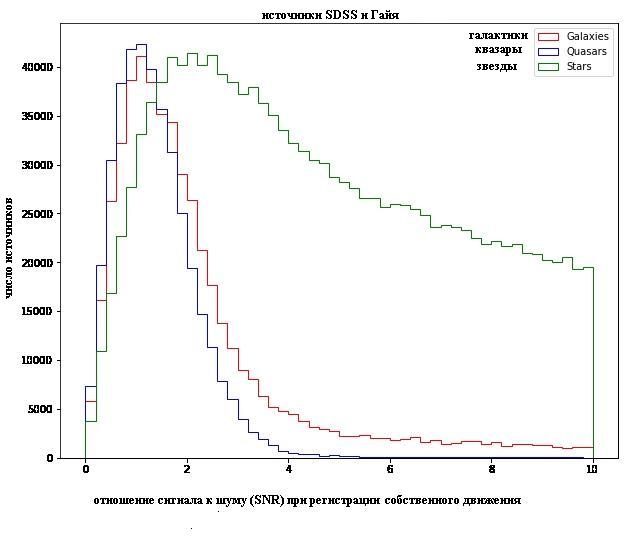
Публикация первых (предварительных) релизов космического телескопа GAIA, который работает в оптическом диапазоне, так же смогла зарегистрировать собственные движения некоторых галактик и квазаров
Актуальность регистрации собственных движений внегалактических объектов в последние годы возрастает в связи с поисками темной (скрытной материи). Как известно темная материя была заподозрена на основе аномально высоких лучевых скоростей движения внешних областей многих галактик. В этих случаях лучевые скорости были измерены через анализ спектров. Измерение собственного движения этих аномальных областей позволило бы лучше прояснить этот вопрос.
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!