Что такое овал в геометрии
Что такое овал в геометрии
Простейшим примером овала является эллипс (в частности, окружность).
Содержание
Свойства
Вариации и обобщения
Источники
См. также
Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)
Полезное
Смотреть что такое «Овал» в других словарях:
ОВАЛ — (от лат. ovum яйцо) 1) продолговато круглый. 2) кривая линия, имеющая форму яйца. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ОВАЛ замкнутая продолговато круглая линия. Словарь иностранных слов, вошедших в… … Словарь иностранных слов русского языка
овал — а, м. ovale m., нем. Oval, ит. ovato <лат. ovatus, ovalis яйцеобразный. Продолговатый круг, яйцевидная форма вещи. Бирж. 159. Продолговатая окружность. Даль. Очертание в виде вытянутого круга, в форме яйца. БАС 1. Фигура круглая или овал без… … Исторический словарь галлицизмов русского языка
овал — См … Словарь синонимов
ОВАЛ — (от лат. ovum яйцо) выпуклая замкнутая плоская кривая без угловых точек, напр. эллипс … Большой Энциклопедический словарь
Овал — Овал, сын Иоктана (Быт 10:28), родоначальник некой араб. народности; см. Гевал (2) … Библейская энциклопедия Брокгауза
ОВАЛ — ОВАЛ, овала, муж. (франц. oval от лат. ovum яйцо). Яйцевидное очертание; фигура, ограниченная кривой линией яйцеобразной формы. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
-овал-(ый) — суффикс Словообразовательная единица, выделяющаяся в имени прилагательном со значением возрастного признака, названного именем существительным, от которого соответствующее имя прилагательное образовано (годовалый). Толковый словарь Ефремовой. Т.… … Современный толковый словарь русского языка Ефремовой
ОВАЛ — ОВАЛ, а, муж. Замкнутое яйцевидное очертание чего н. Красивый о. лица. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
овал — (Oval, Bowl) Замкнутая форма некоторых знаков или их частей, образующая окружность или эллипс. Наклон осей овалов [ось симметрии букв овальной формы] – важный гарнитурный признак [характеристики шрифта], характеризующий форму шрифта… … Шрифтовая терминология
Чем отличается эллипс от овала?
Чем отличается эллипс от овала? Данный вопрос часто остается без ответа — хоть эти две фигуры и знакомы всем еще со школьных времен. Но мало кто понимает, в чем разница между ними. И существуют ли вообще какие-либо отличия.
В чем различие?
Официальные определения каждой из фигур звучат достаточно сложно и непонятно.
Но, если откинуть заумные формулы и сложные определения — все намного проще.
Овал можно «растянуть» как угодно. Это может быть практически круг, либо узкая и длинная замкнутая кривая — главное, чтобы ее форма удовлетворяла определению.
Где а — это длинная полуось, b — короткая, а с — фокальное расстояние (от центра до фокуса).
Всем известный круг — это частный вариант эллипса. В этом случае с=0 (т.к. фокус у него один). Полуоси (радиусы) тоже равны.
Построение овалов и эллипсов
Казалось бы, а зачем их вообще строить?
Земная орбита имеет форму эллипса (траектории движения остальных планет и галактик аналогичны).
Практически в любой технике имеются круглые детали — а они при переведении в трехмерную проекцию будут изображаться в форме замкнутых кривых. Подобные примеры можно приводить бесконечно.
Поэтому в технике, космонавтике, астрономии, архитектуре и многих других научных отраслях разнообразные овалы приходится строить регулярно. Эти знания применяют даже люди, далекие от сложных вычислений — например, художники.
Для того чтобы начертить любую из этих фигур, потребуется лишь циркуль, транспортир и линейка. Сам процесс особых сложностей не вызывает, главное внимательность и точность.
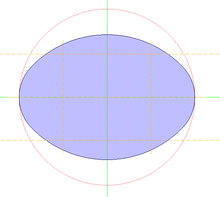
На фото ниже приведен пример построения эллипса в аксонометрии (изометрия).
Формулы и интересные факты
Хоть эти две фигуры и встречаются повсеместно, они до конца не изучены. В школьном курсе их проходят довольно поверхностно, не упоминая о возможных трудностях.
Овалы часто заменяют «правильными» эллипсами, так как с ними работать проще. Но даже в этом случае возникают сложности.
Так, казалось бы, простая задача — вычислить периметр — на самом деле невыполнима. Точной формулы не существует. Это связано с тем, что каждая точка имеет свой собственный радиус кривизны.
Школьникам и людям, далеким от точных вычислений, дают приблизительную формулу. Погрешность у такого результата будет велика, но для примитивных целей это допустимо.
В серьезных расчетах используются совсем другие формулы. Но даже они не дают желаемого результата, так как имеют достаточно большие отклонения от реальных значений.
Так, при расчете траектории движения космического корабля погрешность может достигать нескольких тысяч километров (на дальних расстояниях), а это слишком много. Поэтому поиски «идеальной» формулы ведутся до сих пор.
Овал, свойства овала
Овал, свойства овала.
Овал ― это плоская замкнутая строго выпуклая гладкая кривая.
Овал (понятие и определение):
Овал (фр. ovale, от лат. ovum – «яйцо») ― это плоская замкнутая строго выпуклая гладкая кривая. Овал пересекается с любой прямой не более двух раз.
Овал – это замкнутая выпуклая кривая, очерченная дугами окружностей, плавно переходящих друг в друга.
Овал относится к двухмерным фигурам. Овал имеет правильную форму. Внешне овал напоминает форму яйца.
Точки овала, в которых кривизна овала достигает экстремума, называются его вершинами.
Овал может иметь одну или две оси симметрии, а может и не иметь оси симметрии.
Рис. 2а. Овал с 2 осями симметрии
Рис. 2б. Овал с 1 осью симметрии
Рис. 2в. Овал, не имеющий осей симметрии
Простейшим примером овала является эллипс (в частности, окружность). В свою очередь эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Иными словами, овалом обозначают более общее понятие, а эллипс – это особенное понятие.
Свойства овала:
1. Овал пересекается с любой прямой не более двух раз.
Рис. 4. Овал и прямые
2. Овал имеет не менее четырёх вершин.
3. Если овал имеет в каждой своей точке определённую касательную, то любому направлению на плоскости соответствуют две и только две касательные, параллельные этому направлению.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Значение слова «овал»
[Франц. ovale от лат. ovum — яйцо]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Простейшим примером овала является эллипс (в частности, окружность).
ОВА’Л, а, м. [фр. oval от латин. ovum — яйцо]. Яйцевидное очертание; фигура, ограниченная кривой линией яйцеобразной формы.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
ова́л
1. замкнутая кривая линия, образующая симметричную округлую фигуру вытянутой формы
2. перен. любой объект или контур яйцевидной формы ◆ Скулы и лицо вспыхнули, отчего ещё больше стало видно, что он красив― длинные, до плеч, тёмные волосы почти сходились в овал. Владимир Маканин, «Кавказский пленный», 1995 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: круглоголовый — это что-то нейтральное, положительное или отрицательное?
Овал. Определение овала и способы его построения



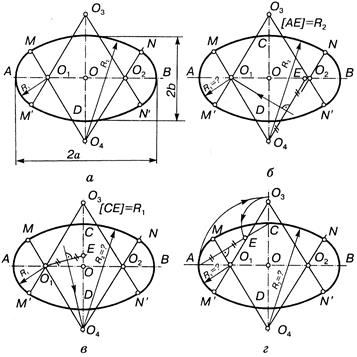
Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а. г).
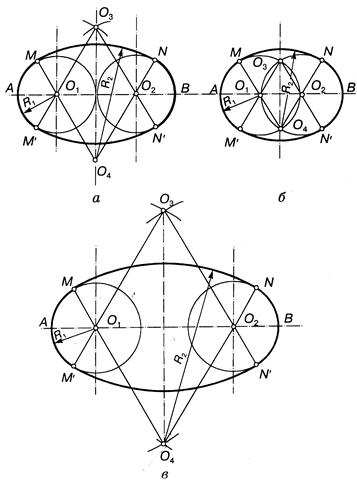
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О1О2 (см. рис. 13.46.а, и рис. 13.46.в), а центры О3 и О4 определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.
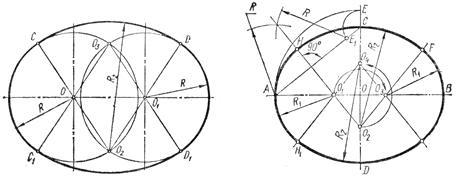
Построение овала с соприкасающимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 01 радиусом, равным, например, расстоянию между их центрами, проводят дуги окружностей до пересечения в точках О2и О3.
Если из точек О2и О3 провести прямые через центры О и O1, то в пересечении с опорными окружностями получим точки сопряжения С, C1, D и D1. Из точек О2и О3 как из центров радиусом R2 проводят дуги сопряжения.
Построение овала с пересекающимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пересечения опорных окружностей С2 и О3 проводят прямые, например, через центры О и O1 до пересечения с опорными окружностями в точках сопряжения С, С1 D и D1, а радиусами R2, равными диаметру опорной окружности,— дуги сопряжения.
Рисунок 3.45 Рисунок 3.46
Построение овала по двум заданным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На вертикальной оси откладываются отрезок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пересечения с отрезком АС в точке Е1. К середине отрезка АЕ1 восстанавливают перпендикуляр и отмечают точки его пересечения с осями овала O1 и 02. Строят точки O3 и 04, симметричные точкам O1 и 02 относительно осей CD и АВ. Точки O1 и 03 будут центрами опорных окружностей радиуса R1, равного отрезку О1А, а точки O2 и 04 — центрами дуг сопряжения радиуса R2, равного отрезку О2С. Прямые, соединяющие центры O1 и 03 с O2 и 04 в пересечении с овалом определят точки сопряжения.
В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:
1. имеют точку соприкосновения;
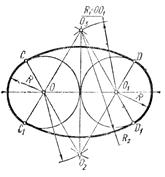
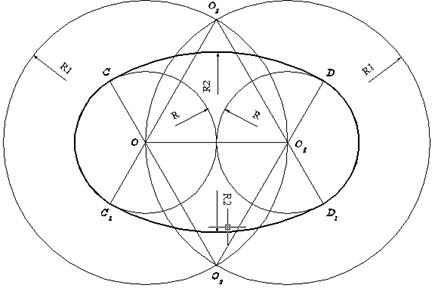
Рассмотрим первый случай. Строят отрезок OO1=2R, параллельный оси Х, на его концах (точки О и О1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R1=2R. Из точек пересечения вспомогательных окружностей О2 и О3 строят дуги CD и C1D1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C1D1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.
Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса