Что такое однофакторный эксперимент
Большая Энциклопедия Нефти и Газа
Однофакторный эксперимент
Однофакторный эксперимент предусматривает поочередное варьирование каждого из факторов при фиксированных на некотором уровне значениях остальных факторов. [2]
Спланированный однофакторный эксперимент с четырьмя уровнями фактора был отклонен руководством фирмы, так как охватывал слишком много районов. Он считал, что пятидесятипроцентное снижение расходов на рекламу может привести в соответствующих районах к невосполнимым потерям. [3]
Поэтому однофакторный эксперимент следует признать явно неудовлетворительным для построения модели технической системы. В связи с этим в настоящее время он практически не применяется. Следует отметить, что рассмотренный план обладает свойством рота-табельности. [4]
Спланированный однофакторный эксперимент с четырьмя уровнями фактора был отклонен руководством фирмы, так как охватывал слишком много районов. Он считал, что пятидесятипроцентное снижение расходов на рекламу может привести в соответствующих районах к невосполнимым потерям. [5]
Основные преимущества математического метода планирования экспериментов перед обычным однофакторным экспериментом заключаются не только в значительном сокращении количества опытов, но и в математизации порядка проведения эксперимента, который ранее определялся лишь интуицией исследователя. [10]
Графический метод оптимизации, основанный на проведении серии однофакторных экспериментов ( см. рисунок), является достаточно наглядным и позволяет определять значения параметров, необходимых для получения покрытий с целым рядом заданных значений характеристик. [12]
Мы хотим заниматься исследованием сложных многофакторных систем и понимаем, что однофакторный эксперимент нам не поможет. [14]
Активные и пассивные, однофакторные и многофакторные эксперименты
ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
Библиографический список
Основная литература
Дополнительная литература
Экспериментальные методы исследований обычно объединяются под названием «планирование эксперимента». Планирование эксперимента – это совокупность приемов, позволяющих исследователю разумно поставить эксперимент, сообразуясь с целью исследования, со стремлением получить максимальную информацию при ограниченном числе опытов, а также правильно обработать и интерпретировать результаты эксперимента.
Варьируемыми факторами называются те воздействия на объект исследования, влияние которых изучается в данном эксперименте. Факторы, действуя на объект, изменяют его состояние. Выходной величиной объекта или откликом называется такой параметр, по которому судят об изменении состояния объекта. Варьируемые факторы принято обозначать буквой 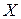
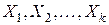
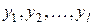
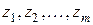
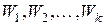
Схематически объект исследования часто представляют в виде так называемого «черного ящика», т. е. объекта, в котором для наблюдения доступны только входные и выходные величины (рис. 1.1). Выходные величины изображены на этом рисунке выходящими стрелками, а факторы – варьируемые, контролируемые и неконтролируемые – входящими стрелками. Названием «черный ящик» подчеркивается полное или частичное отсутствие знаний о внутренней структуре объекта исследования.
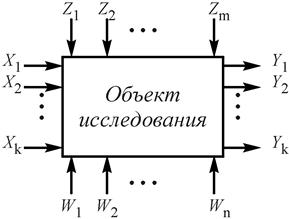 |
| Рис 1.1. Схематическое изображение объекта исследования |
Факторы могут быть количественными и качественными. Количественные факторы можно оценивать количественно, т. е. измерять, взвешивать и т. д. При этом любое значение количественного фактора исчерпывающе и однозначно характеризуется некоторым единственным числом. Примерами количественных факторов являются температура, давление, плотность, скорость, влажность и др. В отличие от количественных факторов между различными значениями одного и того же качественного фактора существует уже не количественное, а качественное отличие. Так, качественным фактором является порода древесины; его возможные значения: древесина сосны, ели и т. д.
Другими примерами качественных факторов являются: конструкция аппарата, вид удобрения, состав связующего, способ обработки.
Каждый фактор принимает в эксперименте одно или несколько значений. Эти значения называют уровнями фактора.
Областью значений фактора называют совокупность значений данного фактора, которые он принимает в эксперименте. Следующее определение применимо только для количественных факторов. Диапазон варьирования фактора – это наименьший отрезок, внутри которого находятся все значения, принимаемые данным фактором в эксперименте. Пусть, например, толщина пилы принимает в эксперименте значения 1,8; 2; 2,2; 2,5 мм. Тогда совокупность приведенных чисел образует область значений данного фактора, а диапазоном его варьирования является отрезок 1,8 … 2,5 мм.
Важным является понятие управляемого фактора. Фактор называется управляемым, если экспериментатор имеет возможность задавать и поддерживать требуемое значение этого фактора в течение всего опыта. Так, управляемыми являются многие режимные факторы технологических процессов. Например, подача в дереворежущих станках, продолжительность прессования и т. д. А такие факторы, как температура окружающей среды, величина сбега бревен, поступающих в распиловку, характеристики износа оборудования, являются неуправляемыми.
Эксперимент, в котором уровни факторов в каждом опыте задаются исследователем, в соответствии с определенным планом, называется активным экспериментом. Для проведения активного эксперимента факторы должны быть управляемыми. Активный эксперимент позволяет воспользоваться рекомендациями теории планирования эксперимента относительно оптимальных значений уровней варьирования факторов и их сочетаний в каждом из поставленных опытов. Например, изучается процесс отверждения полиэфирных покрытий на древесине. При этом исследуется влияние трех факторов: интенсивности облучения ультрафиолетовыми лучами, времени облучения, количества нанесенного лака. Все эти факторы управляемы, поэтому в данном случае может быть поставлен активный эксперимент. Эксперимент, в котором уровни факторов в каждом опыте регистрируются исследователем, но не задаются, называют пассивным экспериментом. В пассивных экспериментах отпадает возможность оптимального выбора уровней варьирования факторов и оптимального сочетания этих уровней в поставленных опытах. Роль экспериментатора здесь сводится в основном к фиксации входных и выходных величин в ходе эксперимента. Примером пассивного эксперимента является исследование влияния возраста деревьев на их диаметр и высоту. Экспериментатор только регистрирует значения варьируемого фактора – возраст деревьев – и выходных величин – диаметр и высоту деревьев. Из-за невозможности целенаправленно задавать уровни факторов эффективность пассивного эксперимента значительно ниже, чем активного. По этой же причине обработка результатов пассивного эксперимента иногда вызывает значительные трудности.
Вопросы, связанные с обработкой результатов активного и пассивного эксперимента, а также некоторые рекомендации по проведению пассивного эксперимента рассмотрены далее.
К совокупности факторов эксперимента предъявляются требования независимости и совместимости. Факторы называются независимыми, если экспериментатор имеет возможность установить значение любого из них на нужном ему уровне независимо от уровней остальных факторов.
Пусть, например, объектом исследования является некоторая масса газа в замкнутом сосуде. Можно ли в качестве варьируемых факторов выбрать объем газа 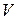
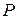
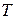
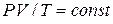
Требование совместимости, предъявляемое к факторам, означает возможность реализации в эксперименте любых комбинаций уровней факторов из области значений. В деревообработке это требование часто вступает в противоречие с условиями функционирования объекта из-за наличия ограничений на управляемые факторы. Таковы, например, ограничения на скорость подачи токарных, фрезерных, круглопильных станков, лесопильных рам по мощности привода механизма подачи, точности обработки, условиям заполнения впадин пилы стружкой (для процессов пиления). Необходимость выполнить требование совместимости заставляет иногда уменьшать диапазон варьирования фактора, или корректировать план эксперимента.
В случаях, если в эксперименте исследуется влияние более чем одного фактора на объект, существуют два разных способа организации эксперимента. Часто здесь говорят о стратегии постановки опытов. В первом случае влияние факторов подвергается исследованию поочередно: сначала варьируется один из них, при этом стабилизируются уровни всех остальных факторов, потом аналогичным образом варьируется только второй фактор, затем третий и т. д. Такой эксперимент называют однофакторным.
Стратегия многофакторного эксперимента в отличие от однофакторного состоит в том, что при переходе к каждому последующему опыту изменяют уровни не одного, а сразу нескольких факторов, т. е. в многофакторном эксперименте варьируются все или почти все факторы одновременно. Однофакторный эксперимент является традиционным способом планирования. Он нагляден: результаты эксперимента зачастую можно прогнозировать, поэтому экспериментатор, хорошо «чувствующий» объект, легко заметит ошибку, вкравшуюся в экспериментальные данные, и примет необходимые меры. Однако главным критерием при выборе той или иной стратегии экспериментирования должна быть его эффективность. Более эффективным считается тот эксперимент, который при прочих равных условиях (одинаковом количестве поставленных опытов) обеспечивает большую точность результатов, например, более достоверное математическое описание объекта или лучшее приближение к точке оптимума. С этой позиции однофакторный эксперимент уступает многофакторному, и преимущества многофакторного эксперимента сказываются тем ощутимее, чем больше факторов варьируется в эксперименте. Например, экспериментатор хочет получить зависимость отклика от четырех варьируемых факторов в виде многочлена второго порядка, и каждый фактор предполагается варьировать на трех уровнях. Тогда эксперимент, предусматривающий исследование всех комбинаций уровней варьирования факторов должен содержать 3 4 = 81 опыт. Это трудоемкое исследование, тем более что каждый опыт придется, по-видимому, повторять некоторое число раз. В то же время на интуитивном уровне совершенно неясно, за счет чего можно уменьшить количество опытов. Так, теория эксперимента для такой ситуации рекомендует, например, план, насчитывающий всего 24 опыта (без учета их повторений). Если при этом известно, как отличаются один от другого результаты опытов при их повторении, то можно оценить точность модели, и, если она недостаточна, увеличить число повторений опытов.
Из-за большей эффективности в теории планирования эксперимента рассматривают почти исключительно многофакторные эксперименты.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Однофакторные, многофакторные, технологические эксперименты.
Поисковый экспериментпроводят в тех случаях, когда затруднена классификация факторов, влияющая на выходной параметр.
В результате эксперимента выявляют значимые и незначимые факторы
влияния. По сути дела, поисковый эксперимент – это пробный эксперимент (теории как таковой нет, но есть предположения, гипотеза).
Лабораторный эксперимент– эксперимент, проводимый в лабораторных условиях с привлечением специальных моделирующих
установок, стендов, оборудования. При этом изучают, как правило, не
сам объект, а его образец. Оценивают влияние одних характеристик
при варьировании других при минимальных затратах времени и ресурсов. Как правило, результаты лабораторного эксперимента необходимо уточнить натурным экспериментом с учетом специфики реального производства.
Натурный эксперимент– эксперимент, который проводится в
производственных условиях на действующем технологическом оборудовании. Он может дать более объективную оценку состояния дел
Простой эксперимент– изучение процесса с предельно небольшим количеством взаимодействующих факторов (максимум три),
Сложный эксперимент– изучение процесса с большим количеством взаимодействующих факторов.
Вещественный эксперимент– эксперимент, предпринимаемый
для изучения влияния различных вещественных факторов на состояние объекта исследования. Например, исследование влияния различных добавок на физико-механические свойства стали; исследование влияния добавок на состояние СОЖ (долговечность, смазывающие и
охлаждающие свойства); исследование влияния добавок на состояние
электролита при реализации размерной электрохимической обработки
(токопроводимость, уменьшение защелачиваемости, улучшение ад-
сорбционных свойств, увеличение степени коагуляции, улучшение
свойств коррозионной защиты); исследование влияния состава износостойкого покрытия на работоспособность режущего инструмента.
Обычный эксперимент– классический эксперимент с тремя составляющими (экспериментатор, объект исследования, средства эксперимента – инструменты, приборы, экспериментальная установка).
Модельный эксперимент– эксперимент, проводимый не с реальным объектом, а с его моделью (материальной или виртуальной
компьютерной копией объекта). Проведение модельного эксперимента
актуально, например, в области автомобиле-, судо- и самолетостроения. Например, «КРАШ-ТЕСТ» автомобиля (вместо реального чело-
века-водителя в автомобиле находится его манекен, исследуется влияние последствий аварийной ситуации на состояние водителя и автомобиля по данным специальных регистрирующих и диагностирующих
приборов); в судо- и самолетостроении для оценки прочности конструкции, аэродинамических свойств, устойчивости и другого прибегают
к использованию моделей судна и самолета (уменьшенные копии реальных объектов), а исследования проводят на специальных испытательных стендах, моделирующих реальные внештатные ситуации.
Однофакторный эксперимент– эксперимент, в рамках которого осуществляется поочередное варьирование интересующими исследователя факторами. Например, алгоритм реализации однофакторного эксперимента при решении многомерной оптимизационной задачи совпадает с алгоритмом метода покоординатного спуска.
Многофакторный эксперимент– эксперимент, при котором в процессе исследования варьируют всеми факторами одновременно и
каждый эффект оценивается по результатам всех опытов, проведенных в данной серии экспериментов. Например, алгоритм реализации
многофакторного эксперимента при решении многомерной оптимизационной задачи совпадает с алгоритмом метода перебораварьируемых параметров.
Технологический эксперимент– эксперимент, направленный на изучение элементов технологического процесса. Например, может идти речь об исследовании устойчивости технологического процесса или
отдельной технологической операции по критерию – устойчивость.
Что такое однофакторный эксперимент
Методика проведения однофакторного эксперимента: из группы факторов (переменных), влияющих на функцию отклика, выбирают один, остальные поддерживают постоянными.
Классический однофакторный эксперимент: каждый их факторов Xj поочередно варьируется на двух уровнях – верхнем Xjmax =+1 и нижнем Xjmin=-1, остальные факторы поддерживают на основном уровне Х=0.
Как правило, при проведении однофакторных экспериментов выбранный интервал D Xj делят на несколько отрезков. Шаг может быть как постоянным, так и переменным. Сняв зависимости yj=f(xj), анализируют каждую из них. Для этого пользуются процедурами аппроксимации или регрессионного анализа.
Задачей регрессионного анализа является вычисление параметров и статистическое исследование математических моделей, полученных на основе экспериментальных данных, часто без учета механизмов и физической сущности процессов и явлений. Полученная таким образом функция y=f(x) называется уравнением регрессии или моделью. Параметры модели называются коэффициентами регрессии. Поверхность, описываемая уравнением регрессии и являющаяся геометрическим образом процесса, называется поверхностью отклика.
Если одному значению х соответствует несколько значений (совокупность) у, то такие модели называют регрессионными (корреляционными). Каждому значению аргумента х соответствует статистический ряд распределения отклика у. Если между х и у существует зависимость, т. е. с изменением х меняется и у, то говорят, что эти величины коррелированны. Критерием оценки этой зависимости служит коэффициент корреляции r. Если есть ряд У(Х), то выборочный коэффициент корреляции


Не всякое значение выборочного коэффициента корреляции является достаточным для статистического обоснования выводов о наличии действительно надежной корреляционной связи между фактором и откликом. Надежность статистических характеристик ослабевает с уменьшением объема выборки (n).
Так, при n=2 через две экспериментальные точки можно провести только одну прямую и зависимость будет функциональной, при этом выборочный коэффициент корреляции равен единице (rxy =1). Однако это не означает надежность полученных статистических характеристик в силу малого объема выборки. Значит, вычислять коэффициент корреляции по результатам двух наблюдений бессмысленно, так как он заведомо будет равен единице, и это будет обусловлено не свойствами переменных и их взаимным отношением, а только числом наблюдений.
В связи с этим требуется проверка того, насколько значимо отличается выборочный коэффициент корреляции rxy от его действительного значения rxy*(при n→∞). При достаточно большом объеме выборки rxy= rxy*.
Таким образом, требуется проверка значимости выборочного коэффициента парной корреляции и оценка его доверительного интервала. Расчет такой оценки см. пример 4.5.
Практически любую зависимость можно описать многочленом n–ной степени:

Кроме этого, в качестве аппроксимирующих функций могут использоваться линейная, показательная, степенная, логарифмическая, гиперболическая и дробно-рациональная.
Для выбора вида аппроксимирующей функции используется следующая методика. Вблизи границ интервала выбирают узлы хa и хb с достоверными значениями у(хa)= уa и у(хb)=уb. Затем рассчитывают
— среднеарифметическое xар=(хa + хb)/2; уар= (уa +уb)/2;
— среднегеометрическое
— среднегармоническое xгр= 2хa хb/(хa + хb); yгр= 2ya yb/(ya + yb).
После этого вычислением или интерполяцией определяют y(xар), y(xгм), y(xгр), вычисляют модули разности согласно таблице 3.2 и по минимальному значению модуля разности выбирают функцию.
Таблица 3.2 Выбор вида аппроксимирующей функции
Модуль разности (минимальное значение)
Однофакторный эксперимент
При использовании метода однофакторного экспериментирования все факторы, кроме одного стабилизируются на одном уровне. При планировании однофакторного эксперимента исследователь определяет необходимый объем данных, структуру модели и осуществляет проверку ее адекватности.
Уравнение математической регрессии целевой функции при однофакторном эксперименте принимает вид у = f ( х ). Нахождение вида функциональной зависимости основывается на методе максимального правдоподобия.
Функция правдоподобия имеет вид:
|
F (εi ) = 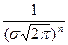
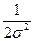

При любом фиксированном значении дисперсии σ 2 максимум функции правдоподобия достигается при наименьшем значении суммы квадратов ошибок (невязок) эксперимента. Значение ошибки в предсказании влияния фактора на процесс по найденному уравнению результата определяется как разность предсказанного значения (вычисленного по найденному уравнению) выхода процесса и полученного в этом опыте значения выхода процесса.
|
∑( yi –f (xi)) 2 =∑εi 2
На практике обработку результатов эксперимента проводят методом наименьших квадратов.
Предположим, что исследуемый процесс описывается линейным уравнением : y=bo+ b1x.
В соответствии с методом наименьших квадратов функция Ф должна быть минимальна.
|
Ф = 

= 
Уравнение в частных производных выглядит следующим образом:
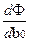

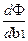

Имеем систему уравнений :
|






Решение системы уравнений имеет вид:
| ||||
N  xi 2 – ( xi 2 – (  xi) 2 xi) 2 |
N | ||||
N  xi 2 – ( xi 2 – (  xi) 2 xi) 2 |
При обработке результатов однофакторных экспериментов с целью получения уравнения регрессии второй степени y=bo+ b1x + b2x 2 необходимо будет минимизировать функцию вида:
Ф = 

|
= 
Нахождение коэффициентов уравнения сводится к решению системы:
|



При нахождении коэффициентов уравнения третьей степени
Решение систем уравнений значительно упрощается, если при планировании эксперимента будет обеспечено равенство 
| ||||
| ||||
 xi 2 xi 2 |
Коэффициенты квадратичного уравнения определяются по формулам:
| ||||
| N | ||||
| ||||
 xi 2 xi 2 | ||||
| ||||
 xi 4 xi 4 |
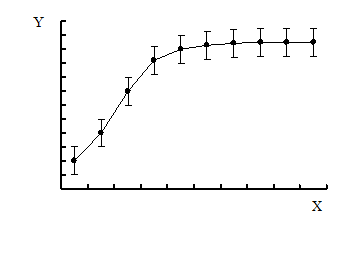
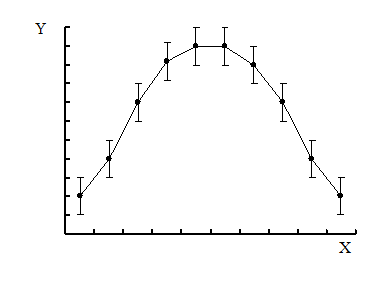
При обработке результатов эксперимента часто пользуются графическим методом. Построение графиков позволяет наглядно изображать полученные зависимости, дает возможность производить графическим путем интерполяцию.
При построении графика масштаб на осях следует выбирать так, чтобы кривая не растягивалась вдоль одной из осей, а лежала по возможности ближе к биссектрисе координатного угла. Кривая проводится через нанесенные на миллиметровой бумаге точки плавно, без резких искривлений. Кривая должна охватывать как можно больше точек и проходить между ними так, чтобы по обе стороны от нее точки располагались равномерно.
Если измерения величины X проводились точнее, чем величины Y, то на графике вместо точек наносятся штрихи, длина которых соответствует точности измерений. Если на графике учитывается точность определения как величины X, так и Y, то штрихи заменяются четырехугольниками погрешностей. Кривая проводится плавно, по возможности через центры штрихов или прямоугольников.
Условия оптимального ведения процесса будет равенство Х=Хopt
|
|
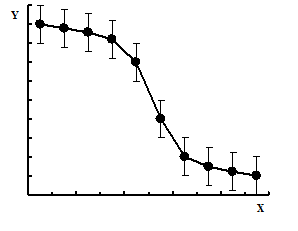
Рис.3 Графики однофакторного эксперимента.
Основные положения планирования многофакторного эксперимента
Для исследования влияния на процесс двух факторов необходимо провести эксперимент при различных сочетаниях изучаемых факторов.
Допустим, что зависимость факторов описывается линейным уравнением вида y=bo+ b1x1 + b2x2.
Для нахождения коэффициентов уравнения из условия :
|
Ф = 

Необходимо решить систему уравнений
|






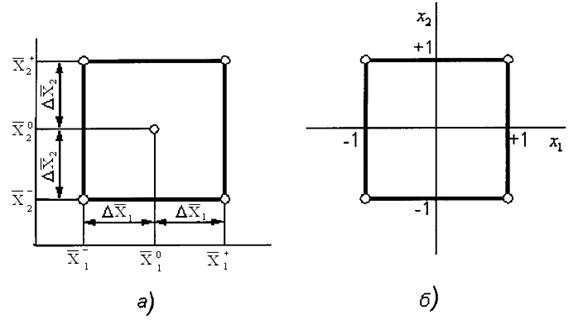
Решение системы уравнений значительно упростится при переходе от натуральных значений факторов в кодированным.
Точка начала эксперимента называется базовой (нулевой) точкой. Это центр плана эксперимента. Базовую точку 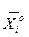
Если область определения фактора непрерывна, выбор масштаба производится согласно формуле
хi = 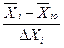
где xi— кодированное значение фактора;
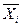
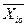
B табл.2 приведен пример кодированных значений для одного фактора, рассчитанных по формуле (13).
Интервал варьирования не может быть меньше погрешности измерения факторa, иначе верхний и нижний уровни окажутся неразличимыми. С другой стороны, интервал не может быть больше пределов области определения, чтобы верхний или нижний уровни оказались за пределами области определения факторов. Поэтому интервал варьирования выбирают равным 0,05. 0,3 от допустимого диапазона изменений факторов, т.е. область варьирования составляет 10. 60% от всего диапазона.
Для упрощения обработки результатов эксперимента и интерпретации результатов переходят от натуральных значений факторов 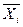
2. Кодированные значения фактора
| Натуральное значение фактора, º С | 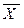 | ||
| Кодированное значение фактора | х | -1 | +1 |
Рис. 4 Симметричный двухуровневый план для двухфакторной функции отклика
При выборе интервала варьирования используют априорную информацию, содержащую сведения о точности измерения факторов, кривизне поверхности отклика и о диапазоне изменения выходной величины. Однако в виду того, что такая информация может оказаться не всегда достоверной, в ходе эксперимента ее нередко приходится корректировать.
Активные эксперименты ставятся таким образом, что в каждом опыте независимые факторы варьируются по специальному плану. Методы активного планирования эксперимента позволяют нейтрализовать пропущенные сочетания уровней.
Матрица планирования полного факторного эксперимента ( ПФЭ)
Согласно этому плану для двухфакторного эксперимента должно быть проведено четыре опыта. Условия проведения эксперимента записываются в виде таблицы, называемой матрицей планирования (матрица Адамара). Каждый столбик матрицы называют вектор-столбцом, а каждую строку – вектор-строкой (табл.3).
Правила построения матрицы планирования эксперимента.
1. В первой строке все факторы устанавливаются на нижнем уровне
3. Все взаимодействия факторов xi·xj для каждой точки факторного пространства получаются перемножением нормированных значений соответствующих факторов.
Проведение ПФЭ позволяет оценить не только силу влияния факторов на отклик, но и эффекты взаимодействия: например, как добавление одних микроингредиентов будет стимулировать влияние других на качество выпускаемого продукта.
3. Матрица планирования ПФЭ 2 2
| Номер опыта | х1 | х2 | y |
| -1 | -1 | y1 | |
| +1 | -1 | y2 | |
| -1 | +1 | y3 | |
| +1 | +1 | y4 |
При построении матрицы ПФЭ 2 2 комбинации уровней находятся прямым перебором. Если количество факторов более двух, используют три приема перехода от матрицы меньшей размерности к матрицам большей размерности.
4. Матрица планирования ПФЭ 2 3
| Номер опыта | х1 | х2 | х3 | у |
| -1 | -1 | -1 | у1 | |
| +1 | -1 | -1 | у2 | |
| -1 | +1 | -1 | у3 | |
| +1 | +1 | -1 | у4 | |
| -1 | -1 | +1 | у5 | |
| +1 | -1 | +1 | у6 | |
| -1 | +1 | +1 | у7 | |
| +1 | +1 | +1 | у8 |
Первый прием основан на том, что при добавлении нового фактора каждая комбинация уровней, имеющихся в матрице меньшей размерности, в матрице большей размерности встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Поэтому сначала описывается исходный план для одного уровня фактора, а затем он повторяется для другого уровня (см. табл. 3).
Матрица планирования эксперимента обладает четырьмя общими свойствами. Два свойства относятся к особенностям построения вектор-столбцов и следуют непосредственно из правил построения матрицы.
Свойства матрицы планирования эксперимента
Второе свойство (условие нормировки): сумма квадратов каждого столбца равна числу опытов, т.е. 
Два других свойства относятся к совокупности столбцов матрицы.
Это правило используется при построении плана эксперимента, то есть при определении каким образом нужно менять значения факторов в опытах. Это правило показывает, что в ортогональном планировании при четном числе уровней, на которых фиксируется каждый фактор, то эти уровни должны быть симметрично расположены относительно центральной точки х=0, при нечетном числе уровней должна использоваться и центральная точка
ПФЭ обладает ортогональной матрицей планирования. Ортогональность позволяет оценивать коэффициенты модели регрессии независимо друг от друга, т.е. избавиться от неопределенности, связанной с неоднозначным оцениванием этих коэффициентов.
Четвертое свойство (ротатабельность): точки в матрице планирования подбираются так, что точность предсказаний значений выходного параметра на основании математической модели одинакова на равных расстояниях от центра эксперимента и не зависит от направления, т.е. дисперсия отклика одинакова на одном расстоянии от центра плана при любом направлении в факторном пространстве. В упрощенном виде это означает, что все точки плана лежат на окружности (сфере, гиперсфере).
Если матрица обладает всеми четырьмя свойствами, то она составлена правильно.
Определение коэффициентов линейной регрессионной модели при планировании эксперимента
|
Рассмотрим вопрос об определении коэффициентов линейной модели, считая, что задачей эксперимента является проверка гипотезы об адекватности модели
После проведения опытов неизвестными величинами в этом выражении будут только коэффициенты b0, b1, b2. Для N опытов можно составить систему линейных условных уравнений. После ее решения методом наименьших квадратов определяются оценки коэффициентов:
bj= 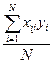
Так, при N=4 получим:
Таким образом, благодаря кодированию факторов расчет коэффициентов превратился в простую процедуру.
Запишем уравнение y = b0 х0 + b1 x1 + b2 x2 для средних арифметических значений переменных.
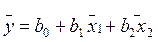
Так как матрица обладает свойством симметрии, то 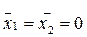
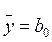
Для того чтобы получить возможность определения b 0 по формуле (15), в матрицу вводят фиктивную переменную х0, которая во всех опытах принимает значение +1. Составленная линейная модель несколько видоизменяется:
Линейная модель не всегда в полной мере описывает объект исследования. Часто нелинейность связана с взаимным влиянием факторов, и задачей полного факторного эксперимента является установление степени такого взаимодействия. Для этого перемножением столбцов матрицы получают новый столбец произведений двух факторов так, что матрица размерности 2 2 будет иметь вид, представленный в табл.4.
5. Матрица планирования эксперимента 2 2 с учетом взаимодействия факторов
| Номер опыта | х0 | х1 | х2 | х1х2 | у |
| +1 | -1 | -1 | +1 | у1 | |
| +1 | +1 | -1 | -1 | у2 | |
| +1 | -1 | +1 | -1 | у3 | |
| +1 | +1 | +1 | +1 | у4 |
С учетом взаимодействия факторов х1х2 видоизменяется модель
Коэффициент b12 вычисляется также по формуле (15) :
Суммарное количество коэффициентов (в том числе b0, линейные эффекты и эффекты взаимодействия) равно числу опытов, проводимых согласно матрице эксперимента. Значения различных коэффициентов независимы друг от друга.
|
Если исследуется трехфакторная модель объекта, для которой функция отклика относительно стандартизированных факторов имеет вид
то матрица планирования ПФЭ выглядит следующим образом:
6. Матрица планирования эксперимента 2 3 с учетом взаимодействия факторов
| № опыта | x0 | x1 | x2 | x3 | х1х2 | х1х3 | х2х3 | х1 х2 х3 | у |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | у1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | у3 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | у4 | |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | у5 | |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | у6 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | у7 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | у8 |
Если модель включает не только линейные эффекты и эффекты взаимодействия, но и квадраты, кубы и т.д. факторов, то подход к оценке коэффициентов несколько иной.
Если, например, при двухфакторном эксперименте заметное влияние имеет квадратичный член, то модель можно записать следующим образом:
Если мы захотим построить матрицу планирования эксперимента с добавлением вектор-столбцов х 2 1 и х 2 2 (табл. 7), то получим единичные столбцы, совпадающие друг с другом и со столбцом х0, в результате чего невозможно определить, за счет чего получилось значение b0. Полученную для такого случая оценку b0 называют смешанной, так как она определяется совместными вкладами свободного и квадратичных членов.
7. Матрица планирования эксперимента 2 2 с учетом квадратичности факторов
| № опыта | x0 | x1 | x2 | x3= х1х2 | х4=х1 2 | х5=х2 2 | у |
| +1 | -1 | -1 | +1 | +1 | у1 | ||
| +1 | +1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | +1 | +1 | у3 | |
| +1 | +1 | +1 | +1 | +1 | у4 |
Итак, полный факторный эксперимент при варьировании факторов на двух уровнях позволяет оценить линейные эффекты эксперимента.
Из-за действия неучтенных (неконтролируемых или неуправляемых) факторов отклик объекта носит случайный характер. Поэтому для каждого сочетания факторов, т.е. в каждой точке факторного пространства, обычно выполняется не один, а серия из m опытов, которые называются параллельными (дублированными). Дублирование позволяет проверить воспроизводимость эксперимента и адекватность модели и исследуемого процесса. В качестве значений отклика принимается среднее арифметическое ỳ i из m измерений. Матрица планирования эксперимента с параллельными опытами представлена в таблице 8.
8. Матрица планирования эксперимента с параллельными опытами
| № | x1 | x2 | . | xK | Параллельные опыты | 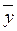 i i | |||
| опыта | . | m | |||||||
| -1 | -1 | . | -1 | у11 | у12 | . | у1m | 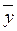 1 1 | |
| +1 | -1 | . | +1 | у21 | у22 | . | у2m | 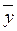 2 2 | |
| . | . | . | . | . | . | . | . | . | . |
| n | +1 | +1 | . | +1 | уn1 | уn2 | . | уnm | 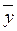 n n |
Планирование дробного факторного эксперимента
Дробный факторный эксперимент, сохраняя все свойства полного факторного эксперимента (симметричность, выполнение условия нормировки, ортогональность, рототабельность), проводится при меньшем числе опытов. Возможность сокращения числа опытов при использовании линейной модели предоставляется в связи с тем, что в полном факторном эксперименте число опытов больше числа коэффициентов модели.
Для пояснения принципа, на котором основано сокращение числа опытов, обратимся к матрице 2 2 полного факторного эксперимента, представленной в табл. 5. Используя эту матрицу, можно вычислить четыре коэффициента модели. Однако при принятом условии линейности модели b12=0 достаточно определить три коэффициента: b0, b1, b3, вектор-столбец х1х2 можно использовать для нового фактора х3.
Если проверить возможность смешивания оценок, то можно заметить, что оно имеет место при различных сочетаниях вектор-столбцов в связи с их совпадением. Однако благодаря тому, что модель линейна, парные взаимодействия незначительны, и взаимодействия практически не влияют на достоверность вычисленных оценок.
Таким образом, оказалось, что для изучения трех факторов достаточно поставить четыре опыта вместо восьми. Сказанное можно обобщить правилом: для сокращения числа опытов новому фактору следует присвоить без изменения знаков вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь.
Матрица 2 2 (табл.5) с заменой х1х2 на х3, представляющая собой половину матрицы 2 3 полного факторного эксперимента, называется полурепликой.
9. Матрица планирования дробного факторного эксперимента 2 3
| Номер опыта | х0 | х1 | х2 | х3 | х1х2 | х1х3 | х2х3 | х1х2 x3 | у |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | у1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | у3 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | у4 |
10. Число опытов при планировании дробных экспериментов.
Таким образом, применение дробного факторного эксперимента позволяет существенно сократить число опытов, необходимых для построения модели (16 вместо 256 при восьмифакторном эксперименте). Наиболее целесообразно использовать дробные реплики для получения линейных моделей с большим количеством факторов.
Проведение обработки результатов эксперимента
Проведение эксперимента, связанного с измерением величин, сопровождается погрешностями измерений, вносящими элемент
неопределенности в результат эксперимента. Постановка повторных или параллельных опытов полностью не исключает неопределенность, так как они проводятся также с погрешностью воспроизводимости.
Дата добавления: 2014-10-17 ; просмотров: 1557 ; Нарушение авторских прав