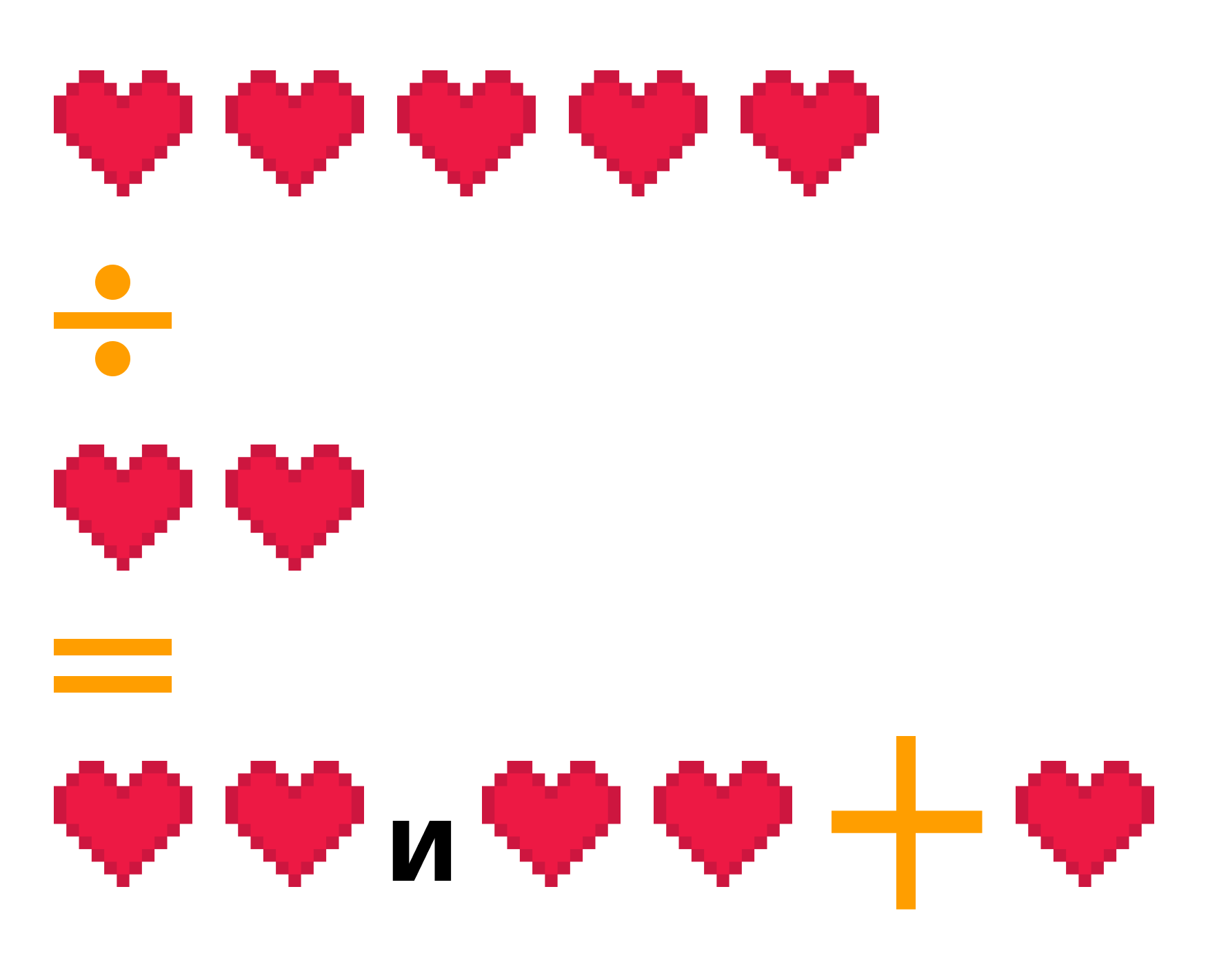Что такое одинаковая четность
Что такое одинаковая четность
Четность и нечетность чисел
Сумма любого числа четных чисел – четно.
Сумма нечетного числа нечетных чисел – нечетно.
Сумма четного числа нечетных чисел – четно.
Идея четности имеет много разных применений. Самые простые из них:
1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).
2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов, если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу переходов между ними и наоборот . )
3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.
3′. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли начальное состояние с конечным. (переформулировка п.3)
4. Если предметы можно разбить на пары, то их количество четно.
5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой предмет может быть не один (но их всегда нечетное число).
(!) Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.
Решение: Нет, не могут. Если бы они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в каком именно направлении вращается первая шестеренка !) Тогда всего должно быть четное число шестеренок, а их 9 штук?! ч.и.т.д. (знак «?!» обозначает получение противоречия)
Четные и нечетные числа
Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.
Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.
Четное число — это число, которое делится нацело на 2.
4 : 2 = 2
Это значит, что 4 — четное число.
Нечетное число — это число, которое не делится на 2 без остатка.
5 не делится на 2 без остатка — значит, 5 это нечетное число.
Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.
Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.
Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.
Свойства четных и нечетных чисел
Четные и нечетные числа чередуются друг с другом
1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.
Задачи для практики
Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.
Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?
| 1 | ♥ | 17 |
| 2 | 10 | ♥ |
| ♥ | 11 | 19 |
| 4 | ♥ | 20 |
| 5 | 13 | ♥ |
| ♥ | 14 | 22 |
| 7 | 15 | 23 |
| 8 | ♥ | ♥ |
Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.
Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | |||||
| X : 2 |
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | 4 | 8 | 12 | 16 | 20 |
| X : 2 | 1 | 2 | 3 | 4 | 5 |
2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное
Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)
Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.
Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?
Ответ: изначально у Маши в инстаграме было 46 фотографий.
Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
| 1 | ☆ | 3 | ☆ | 5 |
| 6 | ☆ | ☆ | 9 | 10 |
| ☆ | 12 | 13 | ☆ | 15 |
| 16 | ☆ | ☆ | 19 | 20 |
| ☆ | 22 | 23 | ☆ | 25 |
Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.
Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70
Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.
Применение свойств четности и нечетности чисел при решении тестовых задач в 5-6 классах средней школы
Введение. Понятие чётности очень важно для развития математической культуры школьника. Теоретически это понятие простое и обычно не вызывает трудностей. Задачи же, связанные с чётностью, могут варьироваться от самых простых до очень сложных. Эти задачи позволяют на простом материале ввести школьника в разнообразный круг математических идей.
Вводная задача 1. Николай с сыном и Пётр с сыном пошли на рыбалку. Николай поймал столько же рыб, сколько его сын, а Пётр — столько же, сколько его сын. Все вместе поймали 27 рыб. Сколько рыб поймал Николай?
Решение. Сначала кажется, что в задаче не хватает данных: два неизвестных и одно уравнение. Затем кто-то должен сообразить, что условия задачи противоречивы. Действительно, отцы поймали столько же рыб, сколько и сыновья. Но тогда общее число рыб должно быть чётным, а по условию оно нечётно.
Вариант рассуждения: Николай с сыном вместе поймали чётное число рыб. То же верно и для Петра с сыном. Значит, и сумма этих чисел чётна. (Если школьники сами не догадаются до одного из этих соображений, следует им немного подсказать).
Но никакого противоречия нет! К противоречию привело неявное предположение о том, что на рыбалке было четыре человека. Но их могло быть и три (Николай — сын или отец Петра). Из условия теперь следует, что все поймали рыб поровну, то есть по 9 штук. С этой задачей (но не с её решением) желательно ознакомить школьников за несколько дней до начала первого занятия. [1]
1. Определение четных и нечетных чисел
Понятие четности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечетные числа соответствовали ян, что означало небо, благоприятность, а четные – это инь, земля, изменчивость, неблагоприятность. В Европе и некоторых восточных странах считается, что четное количество даримых цветов приносит счастье. В России четное количество цветов принято приносить лишь на похороны умершим. В случаях, когда в букете много цветов, четность или нечетность их количества уже не играет такой роли.
Далее идет обсуждение вводной задачи. Она позволяет начать разговор об определении и свойствах чётности. Прежде всего, мы использовали тот факт, что число вида п + п чётно (отцы поймали столько же рыб, сколько сыновья, поэтому вместе они поймали чётное число рыб).
Вот ещё одна задача, иллюстрирующая ту же идею.
Задача 2. Кузнечик прыгал вдоль прямой и вернулся в исходную точку. Все прыжки имеют одинаковую длину. Докажите, что он сделал чётное число прыжков.
Решение. Сколько раз он прыгнул вправо, столько же прыгнул и влево (так как вернулся в исходную точку)… Откуда следует, что число вида п + п = 2п чётно? А это просто определение.
Определение. Целое число называется четным, если оно делится на 2 без остатка, и нечетным, если оно на 2 не делится.
Таким образом, «общий вид» чётного числа 2п, где п — произвольное целое число. Речь идёт именно о целых, а не только о натуральных (то есть целых положительных) числах. В частности, важно понимать, что 0 — тоже чётное число.
Каков же «общий вид» нечётного числа? 2n + 1. Действительно, если от нечётного числа отнять 1, то оно станет чётным, то есть нечётное число равно сумме чётного числа 2п и единицы. Часто используется запись нечётного числа и в виде 2п — 1.
2. Свойства четных и нечетных чисел
Свойство 1. Из определения чётного числа сразу следует, что произведение любого (целого) числа на чётное число чётно. Доказательство: k • 2п = 2(kn).
Свойство 2. Несколько более сложно проверить, что произведение двух нечётных чисел нечётно. Доказательство: (2k + l)(2n + 1) = 2(2kп + k + п) + 1.
Определение. Два целых числа называются числами одинаковой четности, если оба четные или оба нечетные. Два целых числа называют числами разной четности, если одно из них четное, а другое нечетное.
Свойство 3. Сумма двух чисел разной чётности нечётна.
Доказательство: 2k + 2п + 1 = 2(k + п) + 1 = 2m + 1, где m = k + п – целое число. Сумма нечетна.
Свойство 4. Сумма двух чисел одной чётности чётна.
Доказательство: 2k + 2п = 2(k + п) = 2m, где m = k + п — целое число. Таким образом, сумма — четное число.
2k + 1 + 2п + 1 = 2(k + п + 1) = 2m, где m = k + п + 1 — целое число. Таким образом, сумма — четное число.
Обратные утверждения. Затем можно предложить ребятам сформулировать и доказать утверждения, обратные утверждениям о четности суммы.
Если сумма двух чисел нечётна, то слагаемые имеют разную чётность. Доказательство. Действительно, если бы они имели одинаковую чётность, то сумма была бы чётной.
Если сумма двух чисел чётна, то слагаемые имеют одинаковую чётность. Доказательство аналогично.
Перейдем к следующему свойству четных и нечетных чисел.
Задача 3 (подготовительная). Сумма трех чисел нечётна. Сколько слагаемых нечётно? Ответ: одно или три.
Решение. Нетрудно привести примеры, показывающие, что оба случая возможны. Остальные два случая (нечётных слагаемых два или их нет совсем) легко приводятся к противоречию. Теперь можно перейти к наиболее общей формулировке.
Свойство 5. Чётность суммы совпадает с чётностью количества нечётных слагаемых.
Аналогичные рассуждения приводятся для нечетного количества нечетных слагаемых. Учащиеся делают вывод: нечетность суммы совпадает с нечетностью количества нечетных слагаемых.
3. Задачи на применение свойств четности и нечетности [2]
Задача 4. Хозяйка купила общую тетрадь объемом 96 листов и пронумеровала все ее страницы по порядку числами от 1 до 192. Щенок Антошка выгрыз из этой тетради 25 листов и сложил все 50 чисел, которые на них написаны. Могло ли у него получиться 1990?
Решение. На каждом листе сумма номеров страниц нечетна, а сумма 25 нечетных чисел – нечетна. Поэтому число 1990 у Антошки получиться не могло.
Задача 5. В школе 1688 учащихся, причем мальчиков на 373 больше, чем девочек. Доказать, что такого не может быть.
Решение. Если девочек х, то всего учеников 2х + 373, а это число нечетное как сумма четного и нечетного чисел.
Задача 6. Четно или нечетно число 1 – 2 + 3 – 4 + 5 – 6 + … + 993?
Задача 7. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки плюс и минус, чтобы получилось выражение, равное нулю?
Задача 8. Можно ли разменять 100 рублей при помощи 25 монет достоинством 1 и 5 рублей?
Задача 9. В пятиэтажном доме с четырьмя подъездами подсчитали число жителей на каждом этаже и, кроме того, в каждом подъезде. Могут ли все полученные 9 чисел быть нечетными?
Решение. Обозначим число жителей на этажах соответственно через a1, a2, a3, a4, a5, a число жителей в подъездах соответственно через b1, b2, b3, b4. Тогда общее число жителей дома можно подсчитать двумя способами — по этажам и по подъездам:
a1 + a2 + a3 + a4 + a5 = b1 + b2 + b3 + b4. Если бы все эти 9 чисел были нечетными, то сумма в левой части записанного равенства была бы нечетной, а сумма в правой части — четной. Следовательно, это невозможно.
Задача 10. Верно ли равенство 1 2 + 2 3 + 3 4 + … + 99 100 = 20002007?
Решение. Произведения четного и нечетного чисел четны, а сумма четных слагаемых всегда четна.
Задача 11. Четна или нечетна сумма всех натуральных чисел от 1 до 17?
Задача 12. Кузнечик прыгает по прямой: первый раз на 1 см, второй раз на 2 см и т.д. Может ли он через 25 прыжков вернуться на прежнее место?
Решение. Чтобы вернуться на старое место, общее количество сантиметров должно быть четно, а сумма 1 + 2 + 3 + … + 25 нечетна. Поэтому вернуться на прежнее место кузнечик не сможет.
Задачи для самостоятельного решения
Задача 13. Можно ли разменять 25 рублей десятью монетами достоинством 1, 3 и 5 руб.?
Решение. Если мы сложим четное число каких-либо целых чисел, то получим число четное, а 25 — нечетное число. Поэтому разменять 25 руб. таким образом нельзя.
Задача 14. В магазин «Все для собак и кошек» привезли новые игрушки. Могут ли десять игрушек ценой в 3, 5 или 7 рублей стоить в сумме 53 рубля?
Решение. Сумма четного количества нечетных чисел четна. У нас есть 10 чисел (цена одной игрушки), все они нечетные, значит, их сумма должна быть четна. Но 53 – число нечетное, поэтому получить его в виде суммы 10 нечетных чисел нельзя.
Задача 15. У Антона было 5 плиток шоколада. Может ли Антон, поделив каждую плитку на 9, 15 или 25 кусочков, получить всего 100 кусков шоколада?
Решение. Нет, т.к. если сложить 5 нечетных чисел, получим нечетный результат. А число 100 четно.
Задача 16. У Нины было 11 плиток шоколада фабрики «Краскон». Может ли Нина, поделив каждую плитку на 7, 13 или 21 кусочков, получить всего 100 кусков шоколада?
Решение. В выражении нечетное количество нечетных чисел. Ответ должен быть нечетным числом.
4. Задачи на чередование [2]
Свойства чередования:
Задача 18. Может ли вращаться система из 7 шестеренок, если первая сцеплена со второй, вторая с третьей и т.д., а седьмая сцеплена с первой?
Решение. Нет. Если первая вращается по часовой стрелке, то все нечетные шестеренки должны вращаться по часовой стрелке, а первая и седьмая одновременно вращаться по часовой стрелке не могут.
Задача 19. Может ли конь пройти с поля a1 на поле h8, побывав по дороге на каждом из остальных полей ровно один раз?
Решение. Нет, не может. Так как конь должен сделать 63 хода, то последним (нечетным) ходом он встанет на поле другой четности, нежели a1; но h8 имеет тот же цвет.
Задача 20. Все костяшки домино выложили (соблюдая правила игры) в одну длинную цепь. На одном конце этой цепи оказалось 5 очков. Сколько очков может быть на другом конце цепи?
Решение. Если где-то лежит костяшка ∗ − 5, то рядом с ней лежит костяшка 5 − ∗ — возникает разбиение на пары. Сколько костяшек с пятеркой всего? Все ли они в этом разбиении на пары участвуют?
Задачи на разбиение на пары [2]
Свойство: если предметы можно разбить на пары, то их количество четно.
Решение. Если бы такое было возможно, то все звенья ломаной разбились бы на пары пересекающихся. Однако тогда число звеньев должно быть четным.
Задача 22. Семь тринадцатируков с планеты Тринадцатирук решили устроить турнир по армреслингу. Смогут ли они одновременно провести поединки для всех своих рук, чтобы все руки принимали участие, и в каждом поединке встречалось ровно две руки?
Решение. Тринадцатируки не смогут провести поединки для всех рук одновременно, так как в каждом поединке принимает участие две руки, а всего рук 13 · 7 = 91.
Задача 23. В народной дружине 100 человек и каждый вечер трое из них идут на дежурство. Может ли через некоторое время оказаться так, что каждый с каждым дежурил ровно один раз?
Решение. Так как на каждом дежурстве, в котором участвует данный человек, он дежурит с двумя другими, то всех остальных можно разбить на пары. Однако 99 – нечетное число.
1. Медников Л. Э. Четность. – 4-е изд., стереотип. – М.: МЦНМО, 2013.
2. Генкин С. А., Итенберг И. В., Фомин Д. В. Ленинградские математические кружки: пособие для внеклассной работы. Киров, издательство «АСА», 1994.
Проект ученика 6 класса «Задачи на чётность»
Министерство общего и профессионального образования
«Управление образования городского округа Краснотурьинск»
МОУ «СОШ №19 с углублённым изучением предметов
Исполнитель: Медведев Михаил
Руководитель: Синаева Роза Ивановна
2. Теоретическая часть ………………………………………………..стр.4
3. Практическая часть
3.3 Разбиение на пары……………………………………………….стр. 16
«Если написанная программа сработала правильно, то это значит, что во время ее работы выполнилось четное число ошибок»
Правило четности ошибок
Впервые с понятием «четные и нечетные числа» я столкнулся на уроках математики в начальной школе. Участвуя в Российском заочном конкурсе «Познание и творчество» г. Обнинска, Международном конкурсе по математике «Кенгуру» и олимпиаде Уральского Федерального округа часто приходилось решать задачи на четность. Идея четности в решении математической задачи – простая, но глубокая. Она не требует совершенно никакой математической подготовки и в то же время может быть использована для получения неожиданных выводов.
Цель, которую я поставил: углубить и расширить свои знания в области решения задач на четность.
Стремясь извлечь из своих усилий максимальную пользу, я старался подмечать в задаче, которую решаю, то, что может пригодиться при решении других задач. Решение, найденное в результате собственных усилий, может превратиться в образец, которому с успехом можно следовать при решении других задач.
Для реализации поставленной цели мне потребовалось решить следующие задачи:
Изучить литературу по данной теме;
Совершенствовать навыки решения задач на четность и нечетность.
В своем проекте я не в состоянии предложить универсальный метод, но и несколько маленьких шагов в достижении поставленной цели развили мои способности в умении решать задачи.
Известно, что числа бывают четные и нечетные.
Определение: Число называется четным, если оно делится на 2 без остатка.
Формула четного числа – 2с, где с-целое число.
Формула нечетного числа – 2с+1
Идея четности имеет много разных применений.
Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).
Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов, если начало и конец одного вида, то нечетное число. (Четное число объектов соответствует нечетному числу переходов между ними и наоборот)
Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны, то переходов пребывания объекта в том или ином состоянии – четное число, если исходное и конечное состояния совпадают – то нечетное.
По четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.
По числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли начальное состояние с конечным.
Если предметы можно разбить на пары, то их количество четно.
Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой предмет может быть не один (но их всегда нечетное число).
Иногда полезно бывает рассмотрение четности суммы или разности нескольких целых чисел:
Сумма двух четных чисел четна. Сумма двух нечетных чисел четна. Сумма четного и нечетного чисел – нечетна.
Сумма любого количества четных чисел четна. Это очевидно по многим разным соображениям. Например: при последовательном вычислении суммы всегда все промежуточные результаты будут четными, согласно свойству 1. Либо: все четные числа делятся на 2, поэтому из их суммы можно вынести 2 за скобку.
Сумма четного числа нечетных чисел четна, сумма нечетного числа нечетных чисел нечетна.
Доказательство: Если нечетных чисел – четное число (2с), то разобьем их на пары (всего с пар). Сложим числа в каждой паре (сумма двух нечетных чисел – четная). Получим сумму с четных чисел, которая четна (согласно 2). Если же было нечетное число (2с+1) нечетных чисел, то возьмем все числа, кроме одного (2с штук) – их сумма четна. Прибавим к ней оставшееся нечетное число и получим, что сумма всех чисел нечетна по пункту 1.
Сумма нескольких целых чисел четна тогда и только тогда, когда среди них четное число нечетных чисел.
Доказательство: Сложим отдельно все четные и отдельно все нечетные числа. Первая сумма всегда четна (п.2), вторая четна тогда и только тогда, когда в ней четное число нечетных чисел (п.3). Если вторая сумма четна, то сумма всех четна, если она нечетна, то сумма всех нечетна (п.1), поэтому четность суммы всех чисел определяется указанным в условии правилом.
Разность двух четных чисел четна. Разность двух нечетных чисел четна. Разность четного и нечетного чисел в любом порядке – нечетна.
Разность двух чисел имеет ту четность, что и их сумма. Например: 3+2=5 и 3-2=1 – оба нечетны.
Можно доказывать это перебором трех-четырех случаев, но проще заметить, что а+в=(а-в)+2в, т.е. сумма и разность двух чисел различаются на четное число, следовательно, имеют одинаковую четность.
Алгебраическая сумма целых чисел четна тогда и только тогда, когда среди них четное число нечетных чисел.
Противоположные числа имеют одинаковую четность.
Если один из множителей – четное число, то и произведение четно.
Если все множители нечетны, то и произведение нечетно.
Четно или нечетно число 1+2+3+4+…+2000?
Верно ли равенство 1х2+2х3+3х4+…+99х100 = 20002007?
Решение: нет, сумма четных слагаемых всегда четна.
Определить на четность числа 3(х+1); х+х; х+х+2005, если х нечетное.
Можно ли квадрат размером 25х25 разрезать на прямоугольники 1х2?
Решение: нет, число 625 не делится на2.
Можно ли разменять 100 рублей при помощи 25 монет достоинством 1 и 5 рублей?
Кузнечик прыгает по прямой: первый раз на 1 см, второй раз на 2 см и т.д. Может ли он через 25 прыжков вернуться на прежнее место?
Решение: нет, чтобы вернуться на старое место общее количество сантиметров должно быть четно, а сумма 1+2+3+…+25 нечетна.
Можно ли из 37 веревочек сплести сетку так, чтобы каждая веревочка была связана ровно с тремя другими?
Решение: нет, произведение 37х3 нечетно.
В школе 1688 учащихся, причем мальчиков на 373 больше, чем девочек. Доказать, что такого не может быть.
Решение: если девочек х, то всего учеников 2х+373, а это число нечетное.
Произведение двух натуральных чисел умножили на их сумму. Могло ли получиться число 20002007?
Решение: нет, произведение должно быть четно.
Доказать, что n 
Решение: п 
Может ли произведение суммы трех последовательных натуральных чисел на сумму трех следующих за ними натуральных чисел быть равным 33333?
Решение: нет, произведение должно быть четно, т.к.один из множителей четное число.
Решение: в выражении нечетное количество нечетных чисел. Ответ должен быть нечетным числом.
Можно ли составить магический квадрат из первых 36 простых чисел?
Решение: Среди этих чисел одно (2) – четное, а остальные – нечетные. Поэтому в той строке, где стоит двойка, сумма чисел нечетна, а в других – четна.
К 17-значному числу прибавили число, записанное теми же цифрами, но в обратном порядке. Докажите, что хотя бы одна цифра полученной суммы четна.
Решение: Разберем два случая: сумма первой и последней цифр числа меньше 10, и сумма первой и последней цифр числа не меньше 10. Если допустить, что все цифры суммы – нечетны, то в первом случае не должно быть ни одного переноса в разрядах (что, очевидно, приводит к противоречию), а во втором случае наличие переноса при движении справа налево или слева направо чередуется с отсутствием переноса, и в результате мы получим, что цифра суммы в девятом разряде обязательно четна.
Есть 101 монета, из которых 50 фальшивых, отличающихся по весу на 1 грамм от настоящих. Петя взял одну монету и за одно взвешивание на весах со стрелкой, показывающей разность весов на чашках, хочет определить фальшивая ли она. Сможет ли он это сделать?
Решение: Нужно отложить данную монету в сторону, а затем разделить остальные 100 монет на две кучки по 50 монет, и сравнить веса этих кучек. Если они отличаются на четное число грамм, то интересующая нас монета настоящая. Если же разность весов нечетна, то монета фальшивая.
Можно ли выписать в ряд по одному разу цифры от 1 до 9 так, чтобы между единицей и двойкой, двойкой и тройкой, …, восьмеркой и девяткой было нечетное число цифр?
Решение: В противном случае все цифры в ряду стояли бы на местах одной и той же четности.
Двадцать лет тому назад в ходу были купюры достоинством 1, 3, 5, 10 и 25 рублей. Докажите, что если 25 рублей разменяли десятью такими купюрами, то хотя бы одна из этих десяти купюр — десятка.
Решение: Если бы ни одной десятки не было, то число 25 оказалось бы представлено в виде суммы десяти нечетных слагаемых. Но сумма четного количества нечетных слагаемых четна.
Разность двух целых чисел умножили на их произведение. Могли ли получить число
Можно ли натуральные числа 1, 2, …, 20, 21 разбить на несколько групп, в каждой из которых наибольшее число равно сумме всех остальных чисел в этой группе?
Решение: Допустим, что удается осуществить такое разбиение на группы. Если х- наибольшее число некоторой группы, то сумма остальных чисел этой группы тоже равна х и поэтому сумма чисел этой группы равна 2х. Таким образом, сумма чисел каждой группы четна. Следовательно, четна и сумма всех чисел от 1 до 21 ( в самом деле, сначала сложим числа в каждой из групп, а потом сложим полученные суммы; сумма любого количества четных слагаемых четна). Получим противоречие: сумма чисел от 1 до 21 нечетна.
Даны шесть чисел 1,2, 3,4,5,6. Разрешено к любым числам прибавить по единице. Можно ли несколькими такими операциями сделать все числа равными?
Решение: Сумма чисел от 1 до 6 равна 21. Число 21 нечетное. При прибавлении единицы к двум числам сумма увеличивается на 2. Таким образом, сколько бы таких операций ни было, сумма всех чисел будет нечетна. Но сумма шести одинаковых целых чисел четна.
На 99 карточках пишут числа 1, 2, …, 99, перемешивают их, раскладывают чистыми сторонами вверх и снова пишут числа 1, 2, …, 99. Для каждой карточки складывают два ее числа и 99 полученных сумм перемножают. Докажите, что результат четен.
Решение: Произведение целых чисел четно, если четен хотя бы один из сомножителей. Значит, достаточно доказать, что хотя бы на одной карточке сумма чисел четна. Рассуждаем «от противного». Если на всех карточках суммы нечетны, то нечетной будет и сумма всех чисел на всех 99 карточках. Но эта сумма равна удвоенной сумме чисел от 1 до 99. Получили противоречие.
Шахматный конь вышел с некоторой клетки, сделал несколько ходов и вернулся (а) обратно, (б) на клетку того же цвета, с которой он начинал. Доказать, что он сделал четное число ходов.
Решение: (а) Шахматный конь каждым ходом меняет цвет клетки, на которой он стоит. Получаем, что в замкнутой цепочке клеток, по которым прошел конь, чередуются черные и белые. Значит, всего в цепочке четное число клеток. Поскольку она замкнутая, то число ходов будет тоже четным.
(б) На этот раз, поскольку цепочка чередующихся черных и белых клеток под конем не замкнута, то в ней четное число объектов. Получаем неожиданный, на первый взгляд, результат: в цепочке начало и конец одного цвета, поэтому в ней нечетное число клеток. Но надо заметить, что ходы коня – это не объекты цепочки, а переходы между ними. Их здесь (в незамкнутой цепочке) на единицу меньше, чем самих объектов, поэтому число ходов будет четным.
Филя перемножил 17 целых чисел и получил 1025, а Степашка сложил эти же числа и получил 100. Докажите, что кто-то из них ошибся.
Решение: Предположим, что Филя не ошибся. Тогда, если Филя, перемножая натуральные числа, получил нечетный результат, то все множители были четными. Но в тоже время сумма 17 нечетных чисел – нечетное число, и никак не может равняться 100.
На клетчатой бумаге нарисован замкнутый путь (по линиям сетки). Доказать, что он имеет четную длину (сторона клетки имеет длину 1)
Решение: При прохождении пути шагов вверх должно быть столько же, сколько шагов вниз, а шагов вправо – столько же, сколько шагов влево.
Улитка ползет по плоскости с постоянной скоростью, поворачивая на 90 градусов каждые 15 минут. Доказать, что она может вернуться в исходную точку только через целое число часов.
Решение: Вправо улитка должна ползти столько же времени, сколько влево, а вверх – столько же, сколько вниз. Значит улитка проползла чётное число вертикальных и чётное число горизонтальных «пятнадцатиминутных» отрезков. К тому же вертикальные и горизонтальные отрезки чередуются, значит общее их число делится на 4.
Может ли кузнечик за 25 прыжков вернуться в начальную позицию, если он прыгает по диагонали прямоугольника a × b (a и b фиксированы).
Решение: Нет. Если a и b оба нечётны, то каждая координата кузнечика при прыжке меняет чётность. Если же одно из чисел a и b чётно, а другое нечётно, то сумма координат при каждом прыжке меняет чётность. Если же a и b оба чётны, то можно уменьшать их вдвое до тех пор, пока одно из них не станет нечётным, а после этого воспользоваться одним из уже разобранных случаев.
На шахматной доске стоят 8 ладей, которые не бьют друг друга. Доказать, что число ладей, стоящих на черных клетках, четно.
Решение: Цвет клетки определяется суммой её координат. Сумма же координат всех ладей чётна (она не зависит от расстановки и равна 2(1 + 2 + … 8).
В вершинах куба написаны числа 1 и – 1. На каждой грани написано произведение чисел в углах этой грани. Может ли сумма всех написанных чисел быть равна нулю?
Решение: Нет. Чисел всего 14, а их произведение равно 1.
n рыцарей из двух враждующих стран сидят за круглым столом. Число пар соседей-друзей равно числу пар соседей-врагов. Доказать, что n делится на 4.
Решение: Число пар соседей-врагов всегда чётно.
Может ли вращаться система из 7 шестеренок, если первая сцеплена со второй, вторая с третьей и т.д., а седьмая сцеплена с первой?
Решение: нет, если первая вращается по часовой стрелке, то все нечетные шестеренки должны вращаться по часовой стрелке, а первая и седьмая одновременно вращаться по часовой стрелке не могут.
Конь вышел с клетки а1 и через несколько ходов вернулся обратно. Докажите, что он сделал четное количество шагов.
Решение: шахматная доска покрашена в два цвета. С каждым ходом конь меняет цвет клетки. Чтобы вернуться на исходную клетку, коню потребуется четное число ходов.
Можно ли ходом коня обойти все клетки шахматной доски, начав с клетки а1, и закончив на клетке h8 и на каждой клетке доски побывав ровно один раз?
Решение: нет, четные можно поменять местами только с четными, нечетные с нечетными.
Можно ли из 2000 квадратиков со стороной 1см сложить фигуру сложить фигуру с периметром 4001см?
Решение: нет, периметр одного квадратика 4см,при составлении фигуры периметр меняется на четное число см, т.е. периметр с нечетным числом см получить нельзя.
Петя купил общую тетрадь объемом 96 листов и пронумеровал все ее страницы по порядку числами от 1 до 192. Вася вырвал из этой тетради 25 листов и сложил все 50 чисел, которые на них написаны. Могло ли у него получиться 1990?
Решение: На каждом листе сумма номеров страниц нечетна, а сумма 25 нечетных чисел – нечетна.
Произведение 22 целых чисел равно 1. Докажите, что их сумма не равна нулю.
Решение: Среди этих чисел – четное число «минус единиц», а для того, чтобы сумма равнялась нулю, их должно быть ровно 11.
В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки « + » и « – » так, чтобы значение полученного выражения было равно нулю?
Решение: В самом деле, сумма чисел от 1 до 10 равна 55, и изменяя в ней знаки, мы меняем все выражение на четное число.
Можно ли покрыть шахматную доску доминошками 1 × 2 так, чтобы свободными остались только клетки a1 и h8?
Решение: Каждая доминошка покрывает одно черное и одно белое поле, а при выкидывании полей a1 и h8 черных полей остается на 2 меньше, чем белых.
На прямой отмечено 45 точек, лежащих вне отрезка AB. Докажите, что сумма расстояний от этих точек до точки A не равна сумме расстояний от этих точек до точки B.
Решение: Для любой точки X, лежащей вне AB, имеем AX – BX = ± AB. Если предположить, что суммы расстояний равны, то мы получим, что
выражение ± AB ± AB ± … ± AB, в котором участвует 45 слагаемых, равно нулю. Но это невозможно.
По кругу расставлено 9 чисел – 4 единицы и 5 нулей. Каждую секунду над числами проделывают следующую операцию: между соседними числами ставят ноль, если они различны, и единицу, если они равны; после этого старые числа стирают. Могут ли через некоторое время все числа стать одинаковыми?
Решение: Ясно, что комбинация из девяти единиц раньше, чем девять нулей, получиться не может. Если же получилось девять нулей, то на предыдущем ходу нули и единицы должны были чередоваться, что невозможно, так как их всего нечетное количество.
25 мальчиков и 25 девочек сидят за круглым столом. Докажите, что у кого-то из сидящих за столом оба соседа – мальчики.
Решение: Проведем наше доказательство от противного. Занумеруем всех сидящих за столом по порядку, начиная с какого-то места. Если на k-м месте сидит мальчик, то ясно, что на (k – 2)-м и на (k + 2)-м местах сидят девочки. Но поскольку мальчиков и девочек поровну, то и для любой девочки, сидящей на n-м месте, верно, что на (n – 2)-м и на (n + 2)-м местах сидят мальчики. Если мы теперь рассмотрим только тех 25 человек, которые сидят на «четных» местах, то получим, что среди них мальчики и девочки чередуются, если обходить стол в каком-то направлении. Но 25 – нечетное число.
Улитка ползет по плоскости с постоянной скоростью, каждые 15 минут поворачивая под прямым углом. Докажите, что вернуться в исходную точку она сможет лишь через целое число часов.
Решение: Яс но, что количество a участков, на которых улитка ползла вверх или вниз, равно количеству участков, на которых она ползла вправо или влево. Осталось только заметить, что a – четно.
Три кузнечика играют на прямой в чехарду. Каждый раз один из них прыгает через другого (но не через двух сразу!). Могут ли они после 1991 прыжка оказаться на прежних местах?
Решение: О бозначим кузнечиков A, B и C. Назовем расстановки кузнечиков ABC, BCA и CAB (слева направо) – правильными, а ACB, BAC и CBA – неправильными. Легко видеть, что при любом прыжке тип расстановки меняется.
100 фишек поставлены в ряд. Разрешено менять местами любые две фишки, стоящие через одну. Можно ли поставить фишки в обратном порядке?
Решение: Пронумеруем места, на которых стоят фишки. Номера мест, расположенных через одно, имеют одинаковую четность, поэтому после любых разрешенных перестановок фишка, стоявшая изначально на сотом месте, окажется на месте с четным номером. Таким образом, она не сможет оказаться на первом месте, а значит, переставить фишки в обратном порядке не удается.
Существует ли замкнутая 7-звенная ломаная, которая пересекает каждое свое звено ровно 1 раз?
Решение: Допустим, что существует. Тогда пересекающиеся звенья образуют пары. Следовательно, количество звеньев должно быть четным. Получили противоречие.
У марсиан бывает произвольное число рук. Однажды все марсиане взялись за руки так, что свободных рук не осталось. Докажите, что марсиан, у которых нечетное число рук, четно.
Решение: Назовем марсиан с четным числом рук четными, а с нечетным- нечетными. Поскольку руки образуют пары, то общее число рук четно. Общее число рук у четных марсиан четно, поэтому общее число рук у нечетных марсиан тоже четно. Следовательно, число нечетных марсиан четно.
Из полного набора домино, подаренного родителями, Степашка потерял все кости с «пустышками». Сможет ли теперь кто-нибудь выложить оставшиеся кости в ряд?
Решение: Не сможет. Предположим обратное: пусть кости разложены в ряд. Все половинки, кроме двух крайних, объединяются в пары с равными числами. На двух крайних числа могут быть как равными, так и нет. Следовательно, все числа, за исключением двух, заведомо появляются четное число раз. Но после потери всех пустышек осталось ровно по 7 экземпляров каждой из 6 цифр 1,2,3,4,5,6.
Может ли вращаться система из 11 шестеренок, если 1-я сцеплена со 2-й, 2-я – с 3-й и так далее, а 11-я сцеплена с 1-й?
Решение: Нет. Направления вращения шестерёнок должны чередоваться
Существует ли замкнутая 7-звенная ломаная, которая пересекает каждое свое звено ровно 1 раз?
Решение: Допустим, что существует. Тогда пересекающиеся звенья образуют пары. Следовательно, количество звеньев должно быть четным. Получили противоречие.
У марсиан бывает произвольное число рук. Однажды все марсиане взялись за руки так, что свободных рук не осталось. Докажите, что марсиан, у которых нечетное число рук, четно.
Решение: Назовем марсиан с четным числом рук четными, а с нечетным- нечетными. Поскольку руки образуют пары, то общее число рук четно. Общее число рук у четных марсиан четно, поэтому общее число рук у нечетных марсиан тоже четно. Следовательно, число нечетных марсиан четно.
Можно ли соединить 13 городов дорогами, так чтобы из каждого города выходило ровно 5 дорог?
Решение: нет, каждую дорогу считаем дважды, поэтому общее количество дорог должно быть четным. В нашем случае их 13х5 =65.
Можно ли организовать шахматный турнир между 15 шахматистами так, чтобы каждый сыграл по 15 партий?
На плоскости расположено 11 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей, …, 11-я с первой). Могут ли они вращаться одновременно?
Решение: Нет, не могут. Если бы они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки. Тогда всего должно быть четное число шестеренок, а их 11 штук. Получили противоречие.
Полный комплект костей выложен в цепочку. На одном конце оказалась пятерка. А что могло оказаться на другом?
Решение: Рассмотрим множество половинок всех доминошек. Всего доминошек 28, при этом каждое число (от 0 до 6) присутствует ровно на 8 половинках. Заметим, что все половинки, кроме двух крайних, разбиты на пары с одинаковыми цифрами. Это означает, что среди них любое число (от 1 до 6) встречается четное число раз. Тогда, если не рассматривать неизвестный конец, пятерка встречается на одном конце и еще на четном количестве мест, а все остальные числа встречаются на четном количестве мест. Отсюда следует, что на втором конце тоже пятерка.
Существует ли 25-звенная ломаная, пересекающая каждое свое звено ровно один раз?
Решение: Нет. Звенья должны разбиваться на пары пересекающихся
Может ли прямая, не содержащая вершин 1001-угольника, пересекать каждую его сторону?
Решение: Нет. Любые соседние две вершины 1001-угольника должны лежать по разные стороны от прямой.
Можно ли нарисовать 9-звенную замкнутую ломаную, каждое звено которой пересекается ровно с одним из остальных звеньев?
Решение: Если бы такое было возможно, то все звенья ломаной разбились бы на пары пересекающихся. Однако тогда число звеньев должно быть четным.
п рыцарей из двух враждующих стран сидят за круглым столом. Число пар соседей-друзей равно числу пар соседей-врагов. Доказать, что п делится на 4.
Решение: Число пар соседей – врагов всегда четно.
Можно ли нарисовать 9-звенную замкнутую ломаную, каждое звено которой пересекается ровно с одним из остальных звеньев?
Решение: Если бы такое было возможно, то все звенья ломаной разбились бы на пары пересекающихся. Однако тогда число звеньев должно быть четным.
Д вое по очереди ломают шоколадку 6 × 8. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет сделать ход.
Решение: Основное соображение: после каждого хода количество кусков увеличивается ровно на 1. Сначала был один кусок. В конце игры, когда нельзя сделать ни одного хода, шоколадка разломана на маленькие дольки. А их 48! Таким образом, игра будет продолжаться ровно 47 ходов. Последний, 47-й ход (так же, как и все другие ходы с нечетными номерами) сделает первый игрок. Поэтому он в этой игре побеждает, причем независимо от того, как будет играть.
Имеется три кучки камней: в первой – 10, во второй – 15, в третьей – 20. За ход разрешается разбить любую кучку на две меньшие; проигрывает тот, кто не сможет сделать ход.
Решение: После каждого хода количество кучек увеличивается на 1. Сначала их было 3, в конце – 45. Таким образом, всего будет сделано 42 хода. Последний выигрывающий 42-й ход сделает второй игрок.
Числа от 1 до 20 выписаны в строчку. Игроки по очереди расставляют между ними плюсы и минусы. После того, как все места заполнены, подсчитывается результат. Если он четен, то выигрывает первый игрок, если нечетен, то второй.
Решение: Четность результата не зависит от расстановки плюсов и минусов, а зависит только от количества нечетных чисел в первоначальном наборе. Так как в данном случае их 10 (т.е. четное число), то выигрывает первый игрок.
4. Двое по очереди ставят ладей на шахматную доску так, чтобы ладьи не били друг друга. Проигрывает тот, кто не может сделать ход.
Решение: После каждого хода и количество вертикалей, и количество горизонталей, на которые можно поставить ладей, уменьшается на 1. Поэтому игра будет продолжаться ровно 8 ходов. Последний, выигрышный ход будет сделан вторым игроком.
5. На доске написаны 6 единиц и 6 двоек. За ход разрешается стереть две любые цифры и, если они были одинаковыми, написать двойку, а если разными – единицу. Если последняя оставшаяся на доске цифра – единица, то выиграл первый игрок, если двойка – то второй.
Решение: Четность числа единиц на доске после каждого хода не меняется. Поскольку сначала единиц было четное число, то после последнего хода на доске не может оставаться одна (нечетное число!) единица. Поэтому выигрывает второй игрок.
6. На доске написаны числа 25 и 36. За ход разрешается дописать еще одно натуральное число – разность любых двух имеющихся на доске чисел, если она еще не встречалась. Проигрывает тот, кто не может сделать ход.
Решение: В процессе игры (сравните с алгоритмом Евклида) обязательно будет выписан наибольший общий делитель исходных чисел. Следовательно, будут выписаны и все числа, кратные ему, не превосходящие большего из исходных чисел. В нашем случае НОД равен 1. Поэтому будут выписаны все числа от 1 до 36. Таким образом игра будет продолжаться 34 хода (два числа были написаны сначала), и выигрывает второй игрок.
7. Дана клетчатая доска размерами
а) 9 × 10;б) 10 × 12;в) 9 × 11.
За ход разрешается вычеркнуть любую горизонталь или любую вертикаль, если в ней к моменту хода есть хотя бы одна невычеркнутая клетка. Проигрывает тот, кто не может сделать ход.
Решение: Эта игра – не совсем шутка. В ней выигрывающий, допустив ошибку, может проиграть. Эта ошибка состоит в том, что он после своего хода оставляет невычеркнутые клетки только в одном столбце или только в одной строке, предоставляя противнику возможность выиграть в один ход. Проигравшим в этой игре является, тем самым, тот, кто сделает этот роковой ход. Заметим, что оставшуюся после вычеркивания горизонтали часть клетчатой доски m × n можно представить себе как доску (m – 1) × n. Аналогично, после вычеркивания вертикали остается доска m × (n – 1). Ситуация, в которой каждый ход является «роковым», только одна – это доска 2 × 2. Таким образом, выигрывает игрок, после хода которого она возникла. Однако, как мы видели, при каждом ходе суммарное количество горизонталей и вертикалей на доске уменьшается на 1. Поэтому четность этой суммы в начале игры определяет победителя. В пункте а) выигрывает первый игрок, а в пунктах б) и в) – второй. Заметим, что в пункте б) решающим соображением может быть и симметричная стратегия второго игрока.
Цель, которую я поставил перед собой, мной реализована. Работа над проектом вызвала интерес и увлекла меня. Эта работа потребовала от меня не только определенных математических знаний и настойчивости, но и дала мне возможность почувствовать огромную радость самостоятельного открытия.
В своей работе мною решено 66 задач. Известно, что решение задач – это практическое искусство, подобное плаванию или игре на фортепиано. Научиться ему можно только подражая хорошим образцам, постоянно практикуясь. В моем проекте нет волшебного ключа, открывающего все двери, позволяющего решать все задачи. Работа над проектом явилась для меня открытием.
Размышляя над тем, что сделано мною для реализации цели, я пришел к выводам:
Наблюдение может привести к открытию;
Лучший способ изучить что-либо – открыть это самому;
Нужно отыскать в задаче то, что может пригодиться при решении других задач (т.е. обнаружить общий метод);
Эта работа способствовала более глубокому пониманию школьной
программы и расширению кругозора.
Данный материал будет полезен учащимся, интересующихся
математикой. Его можно использовать на некоторых уроках и на факультативных занятиях.