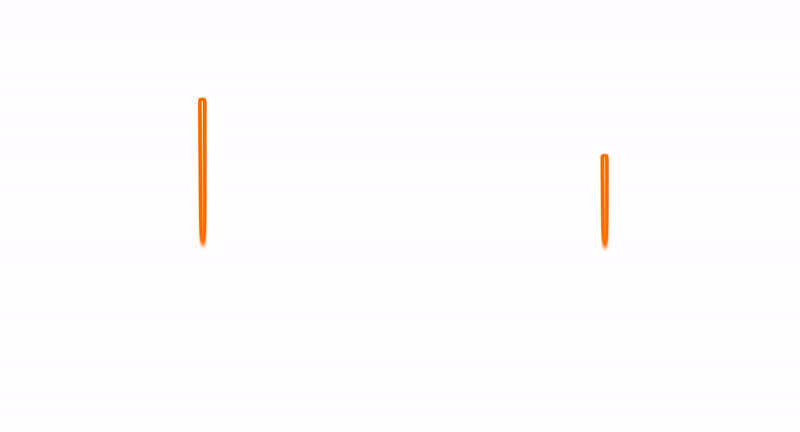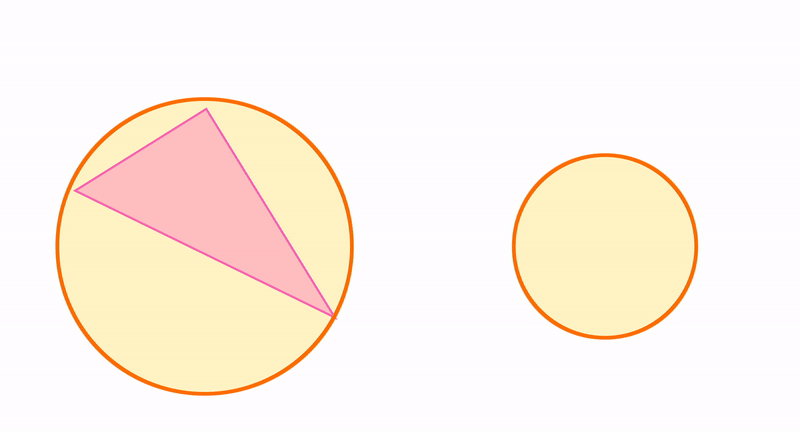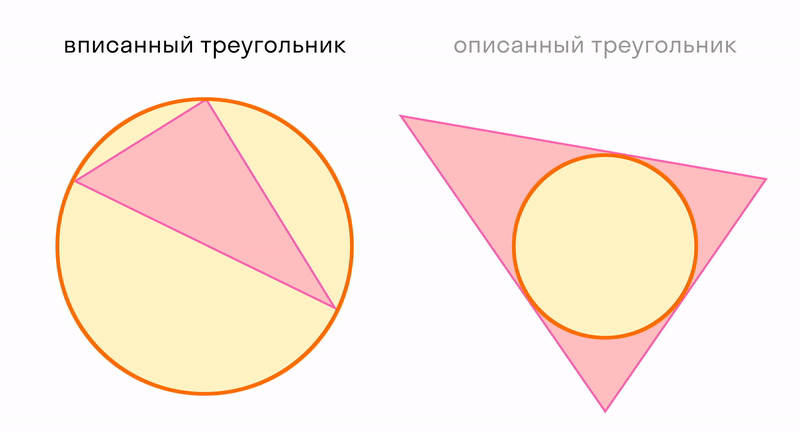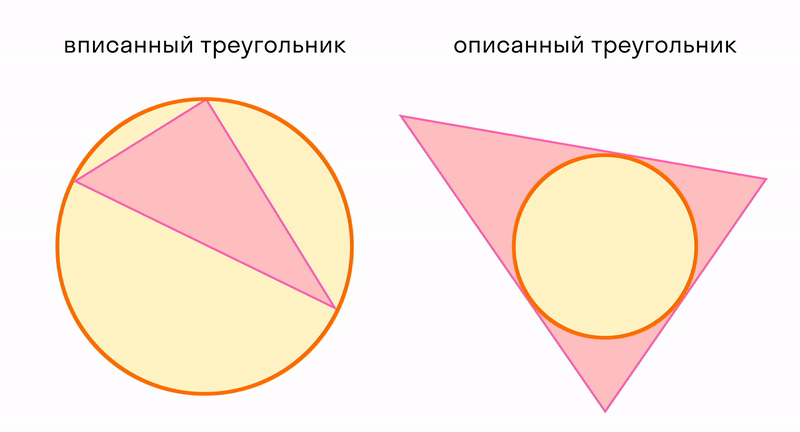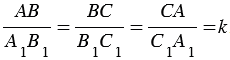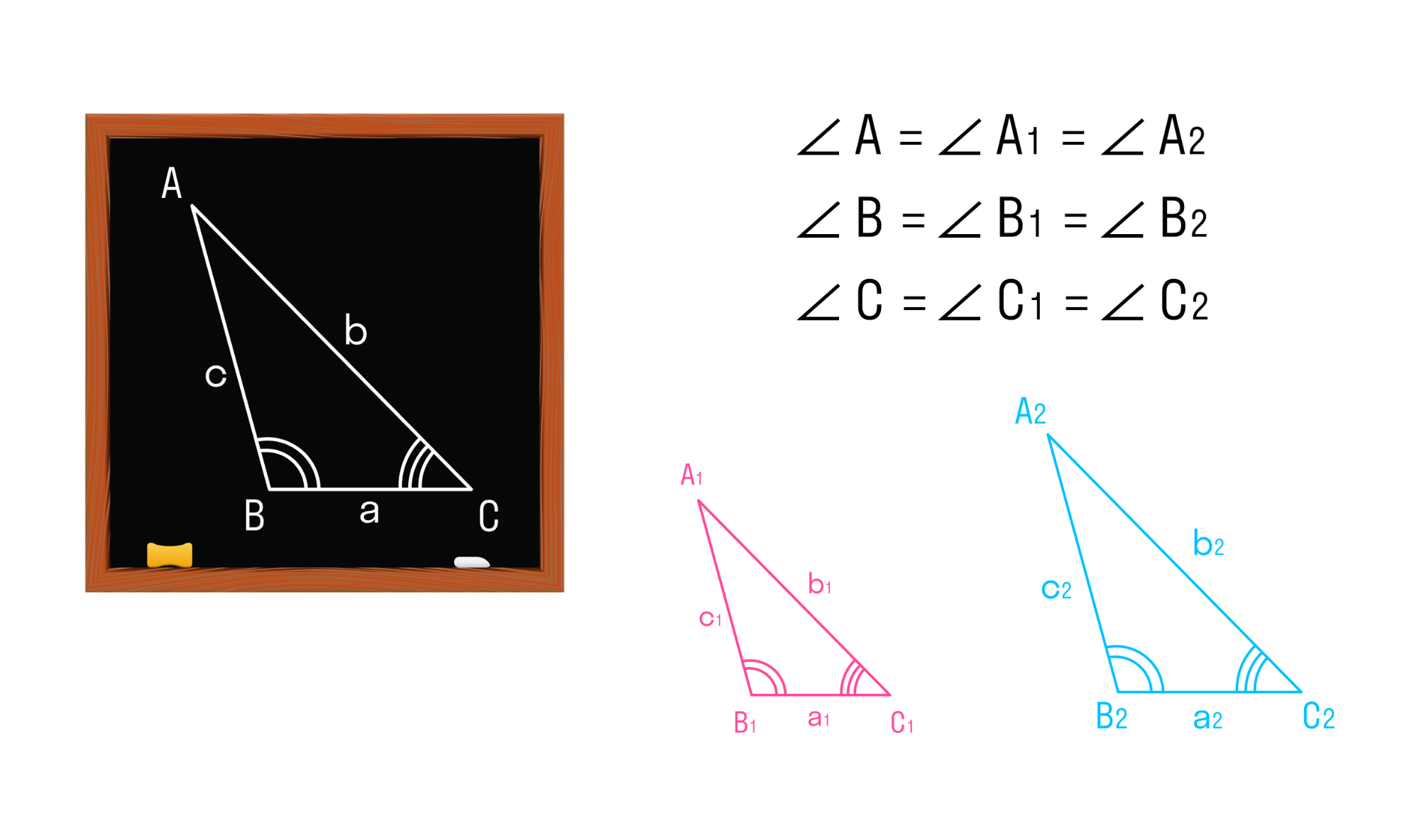Что такое общая в геометрии
Основы геометрии
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
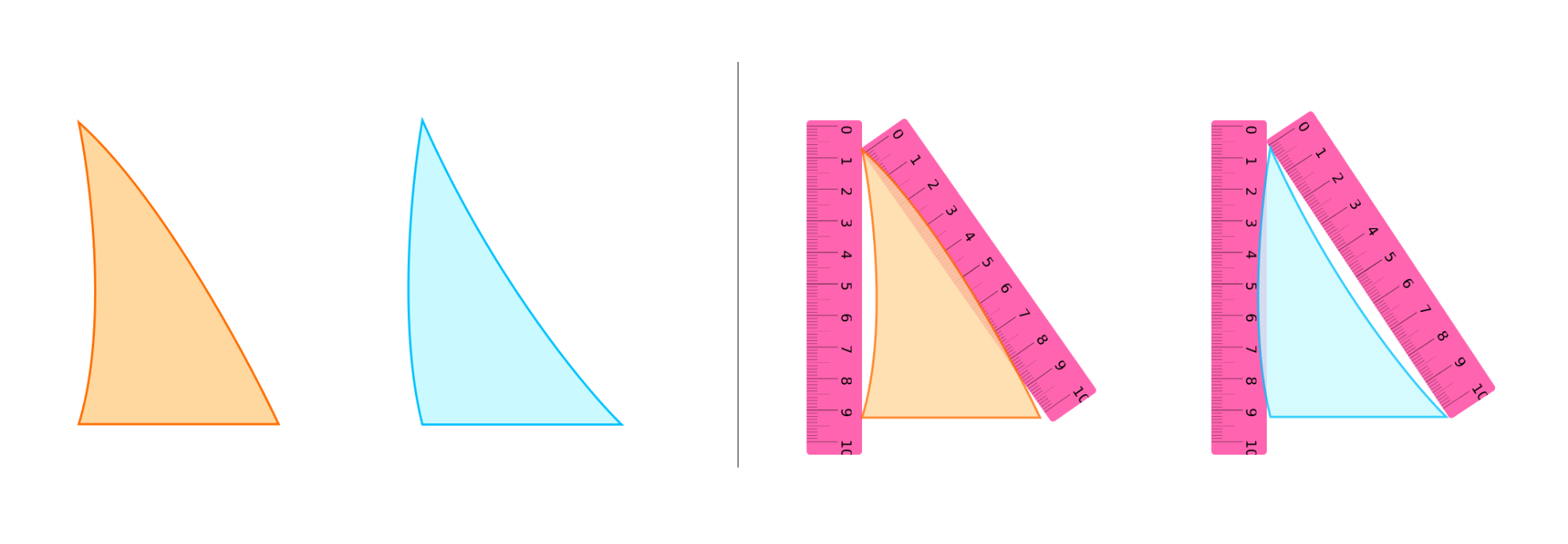
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
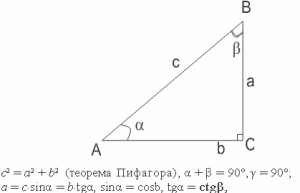
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
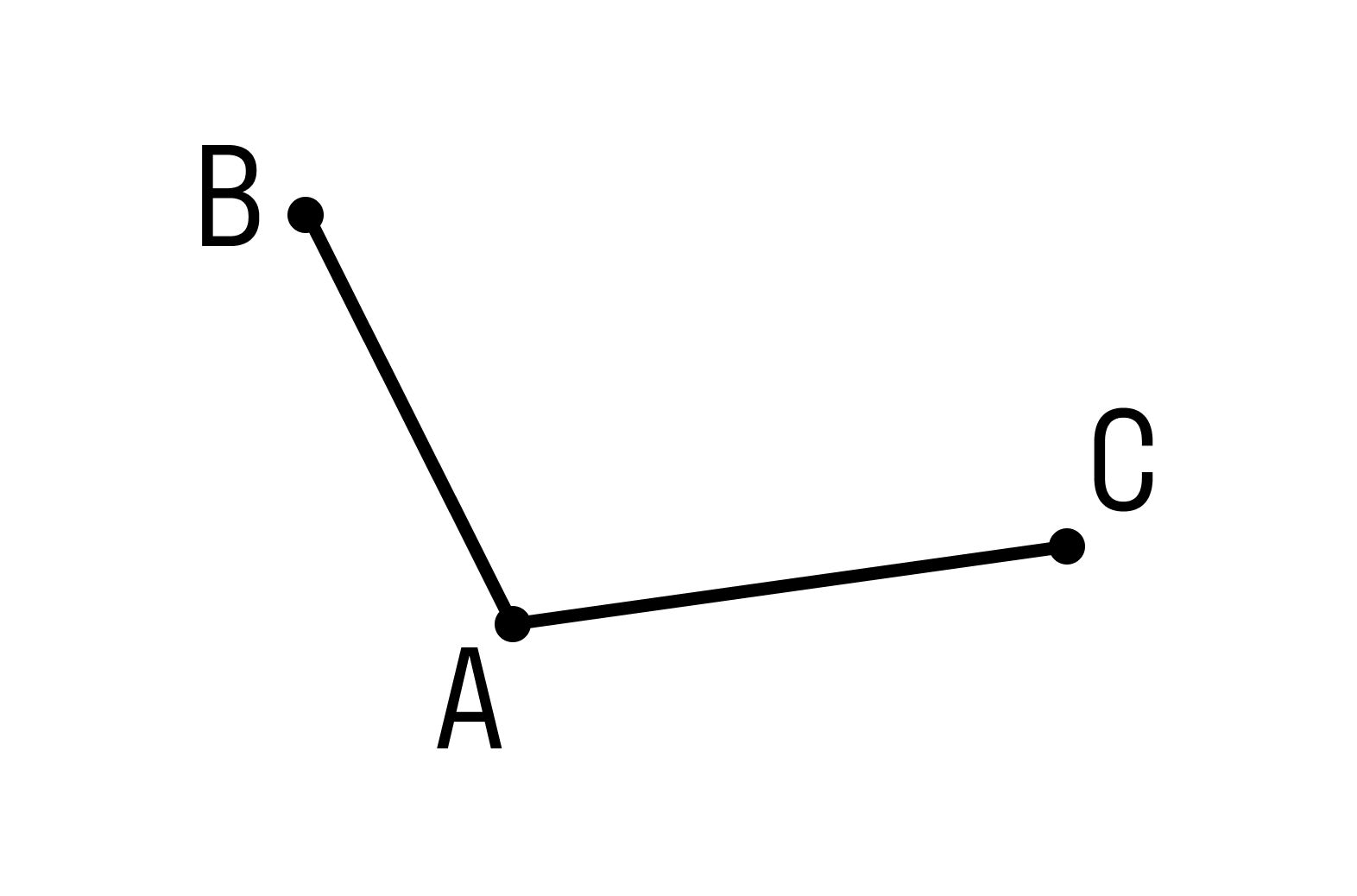
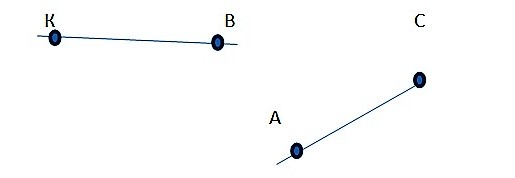
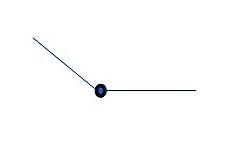
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
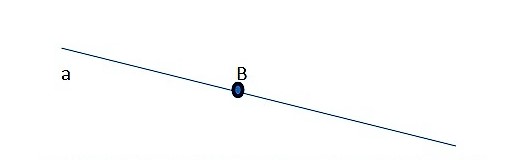
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
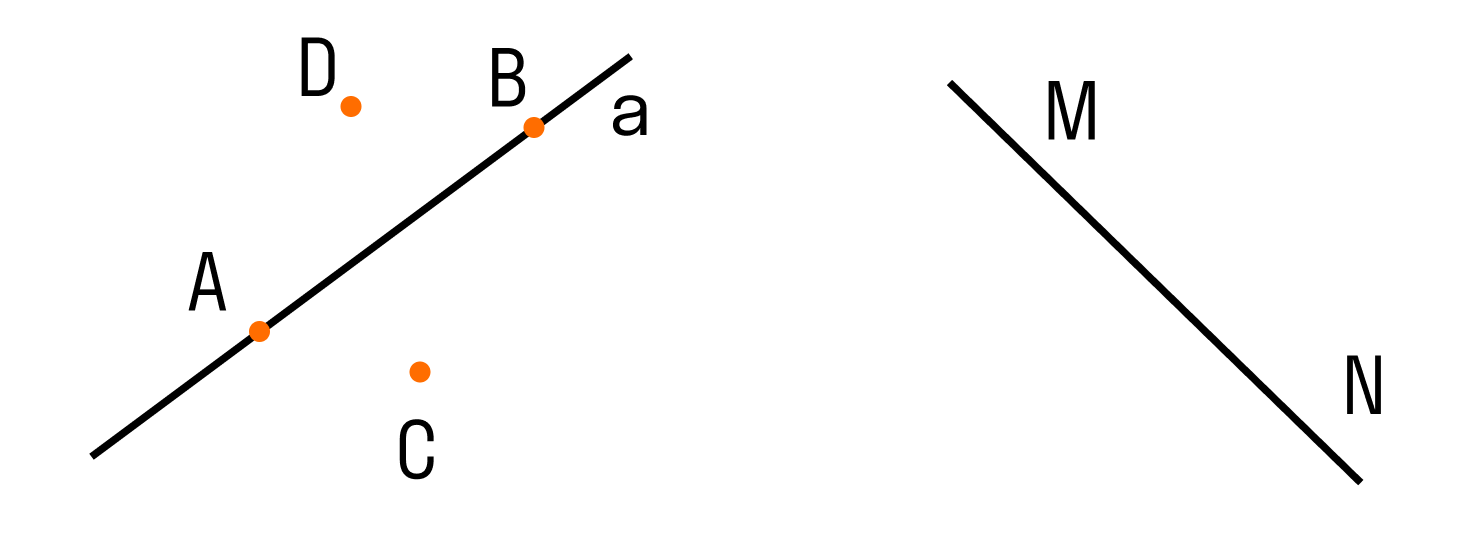
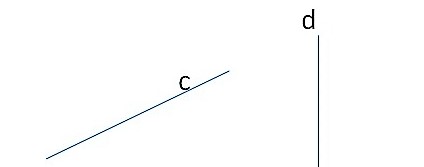
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
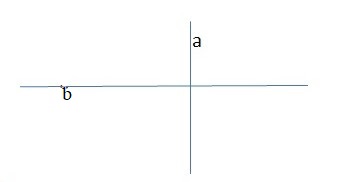
Два варианта расположения точек относительно прямой:
Если рассмотреть две прямые, то возможны два варианта их расположения:
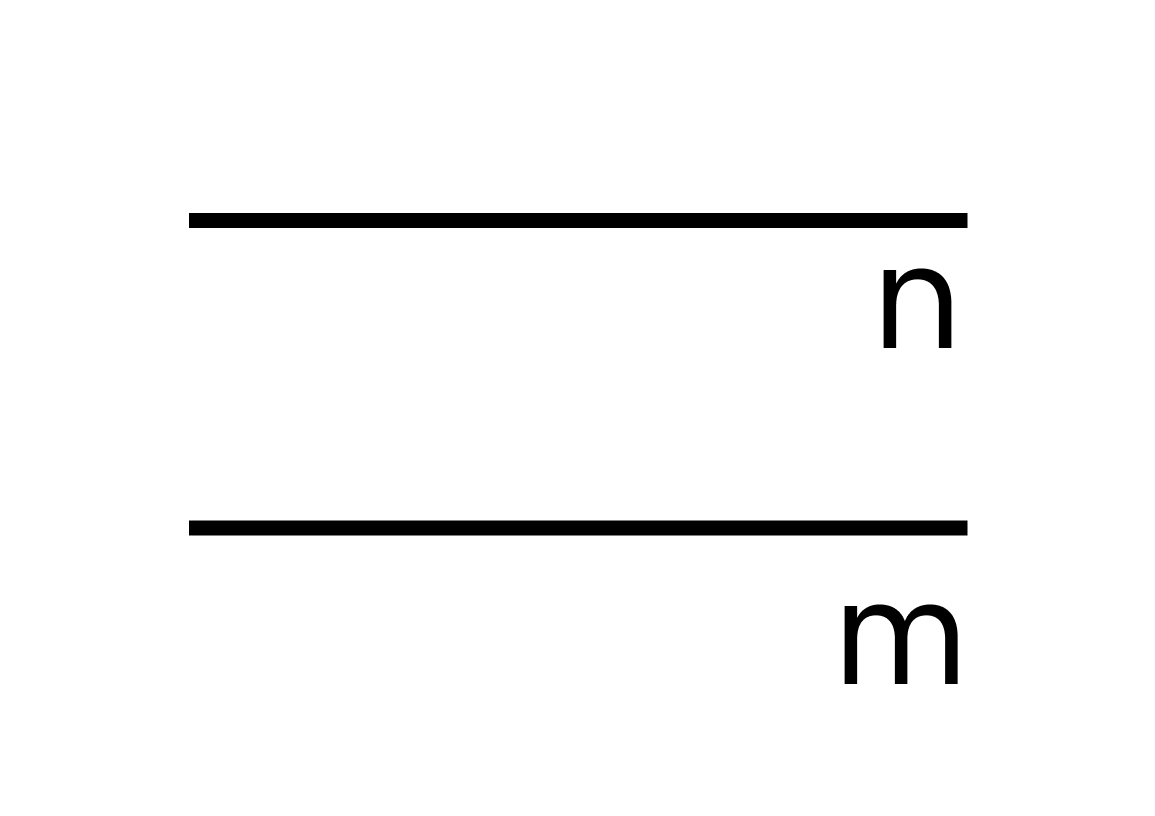
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
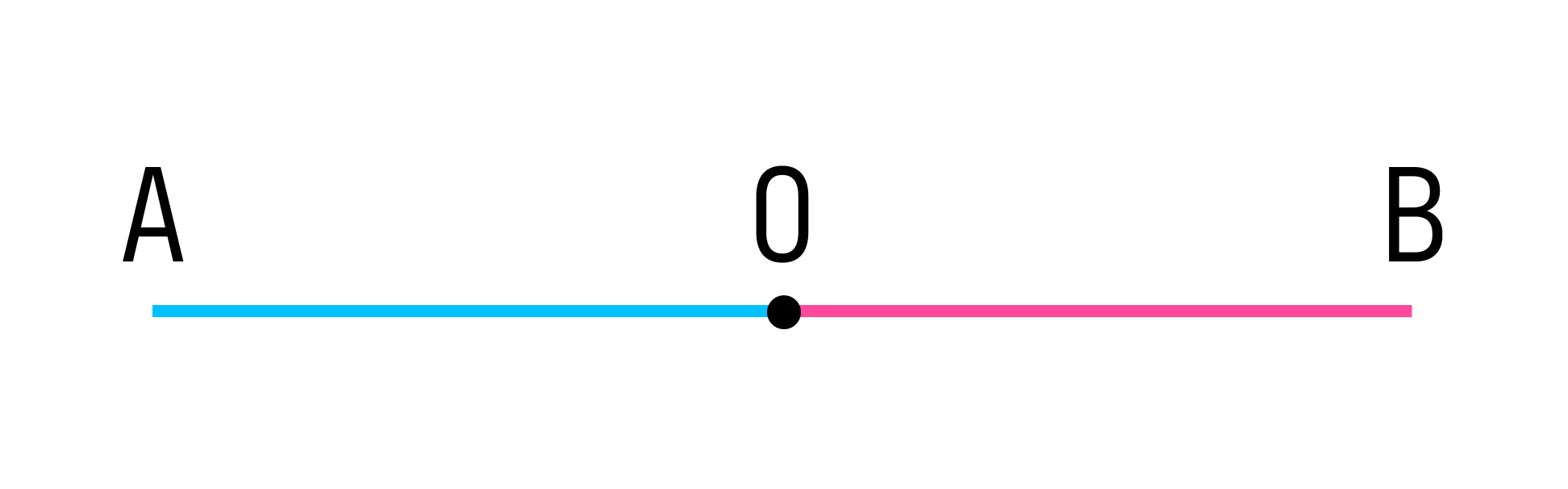
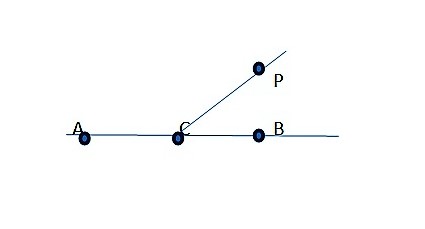
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
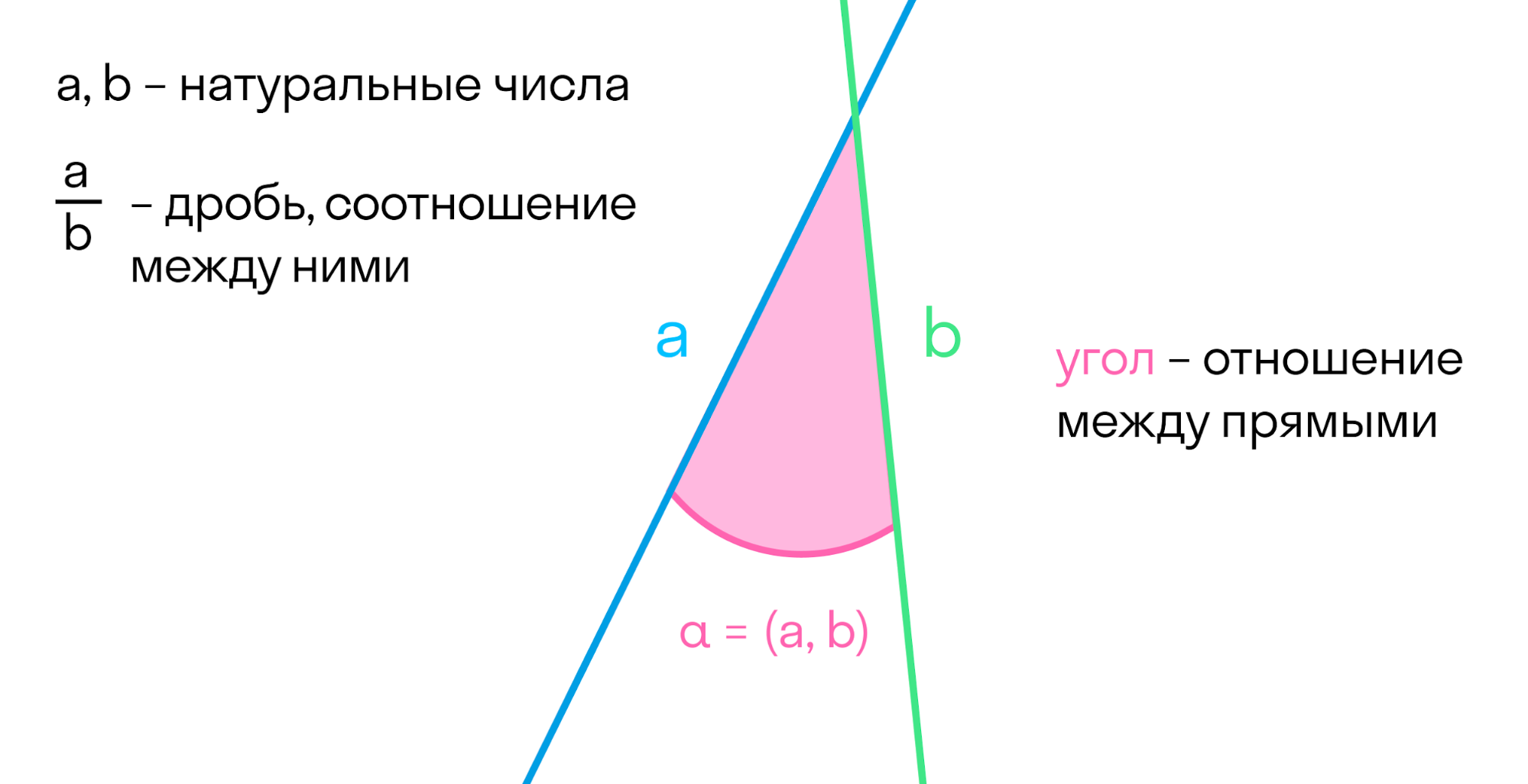
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
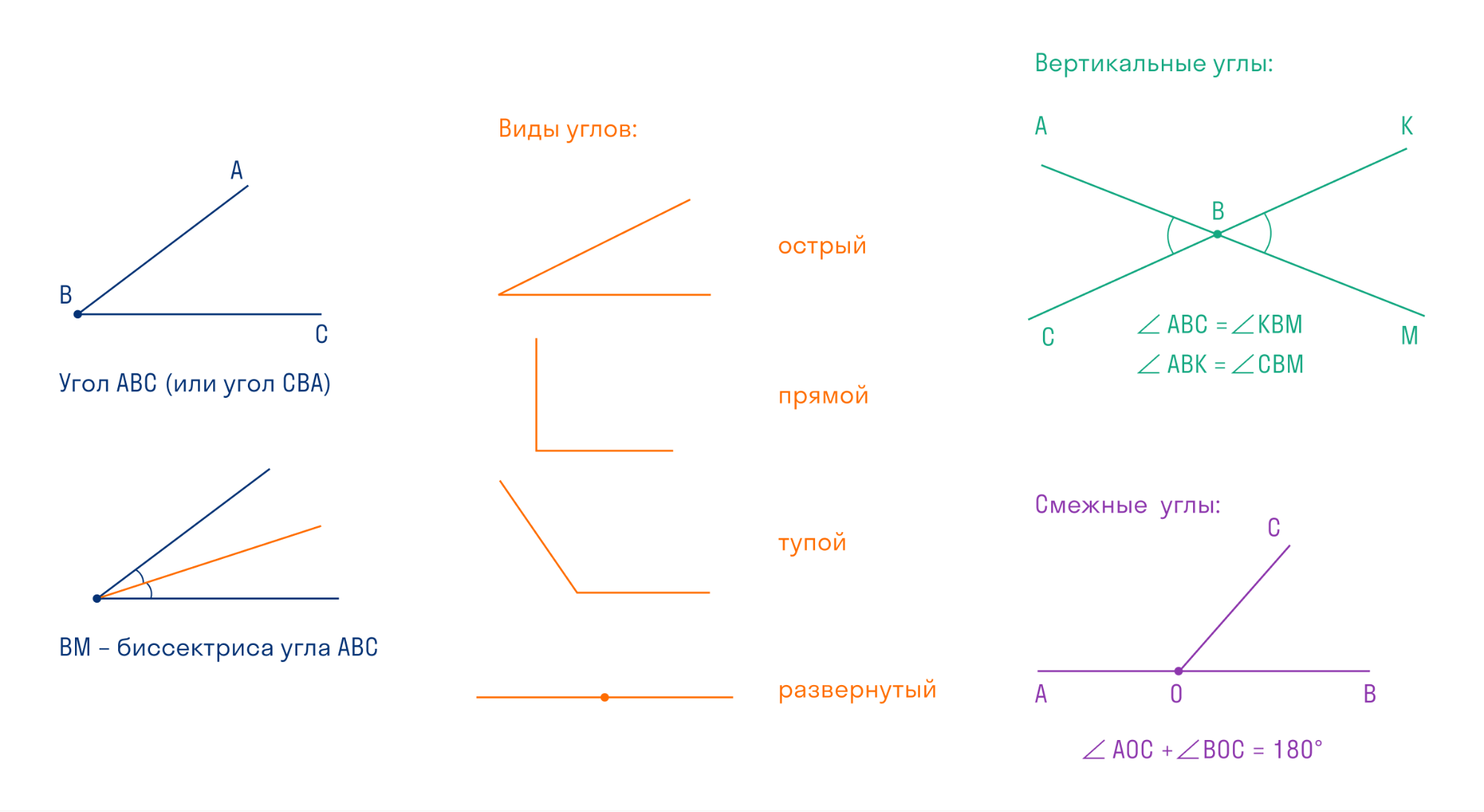
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
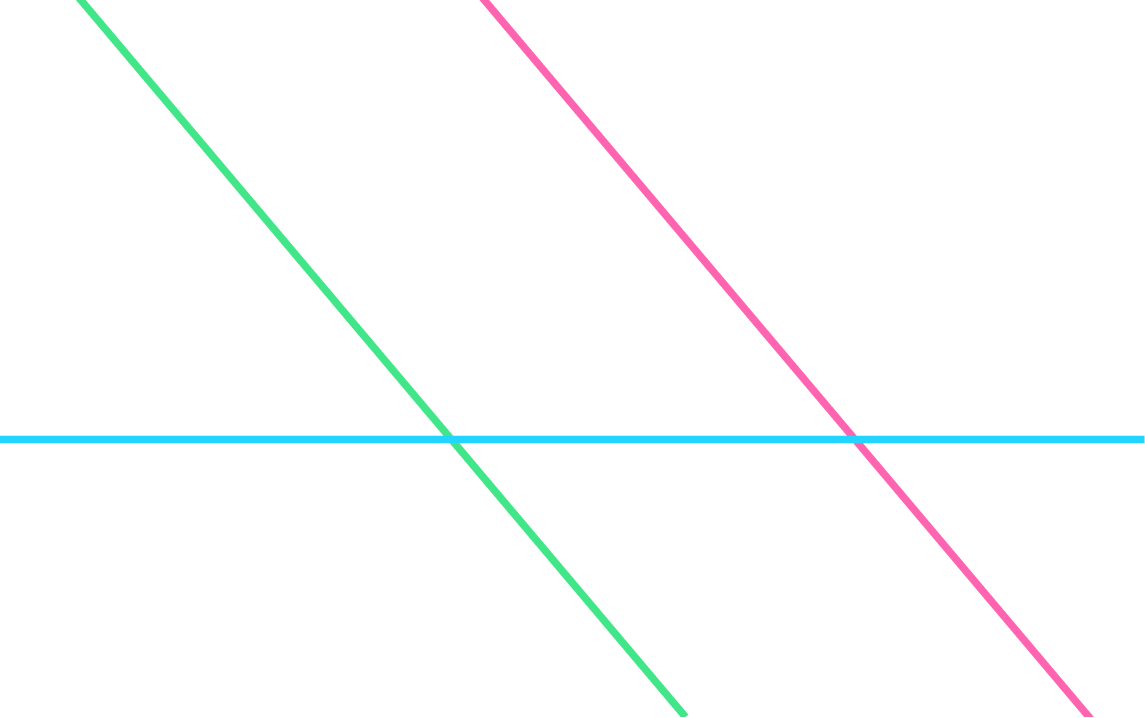
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
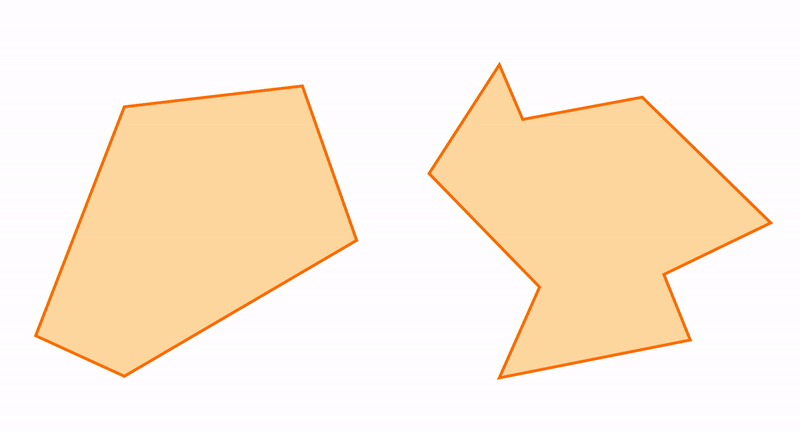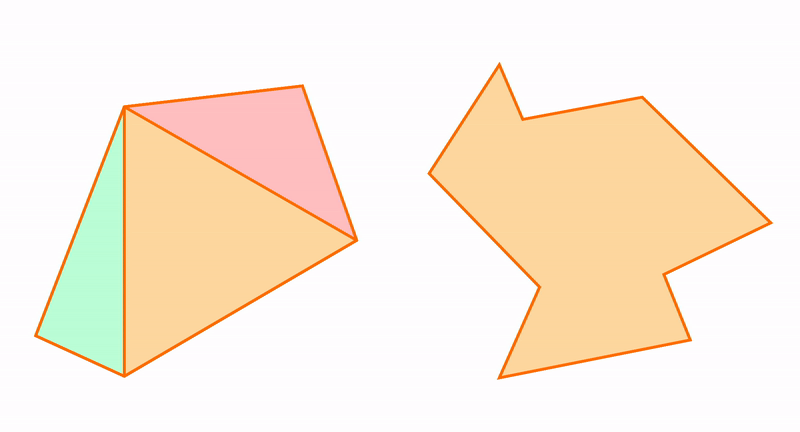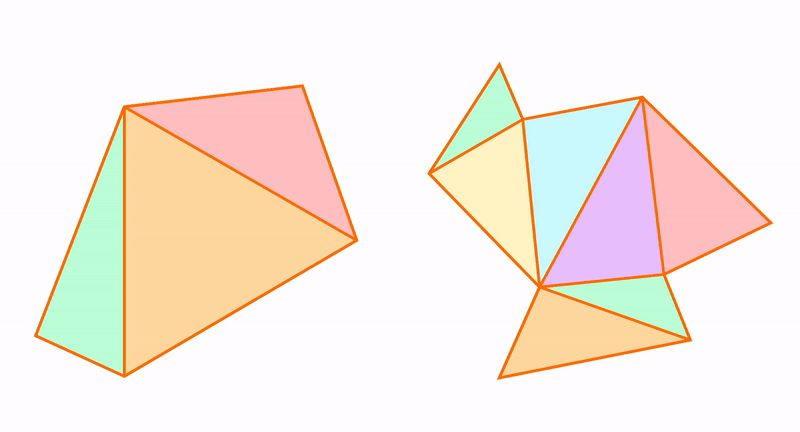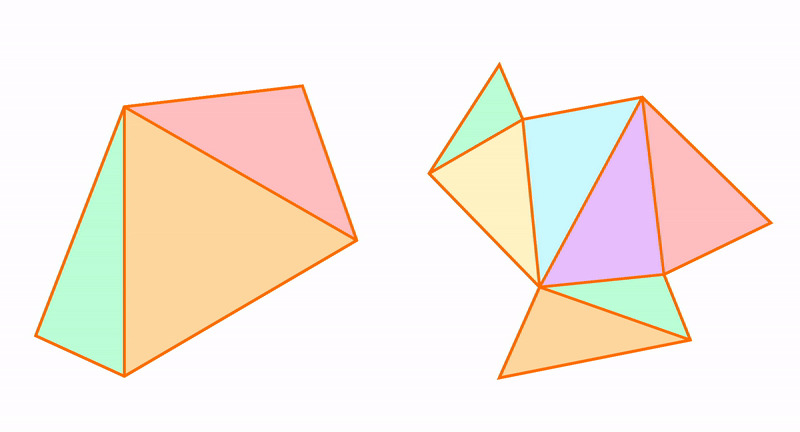
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
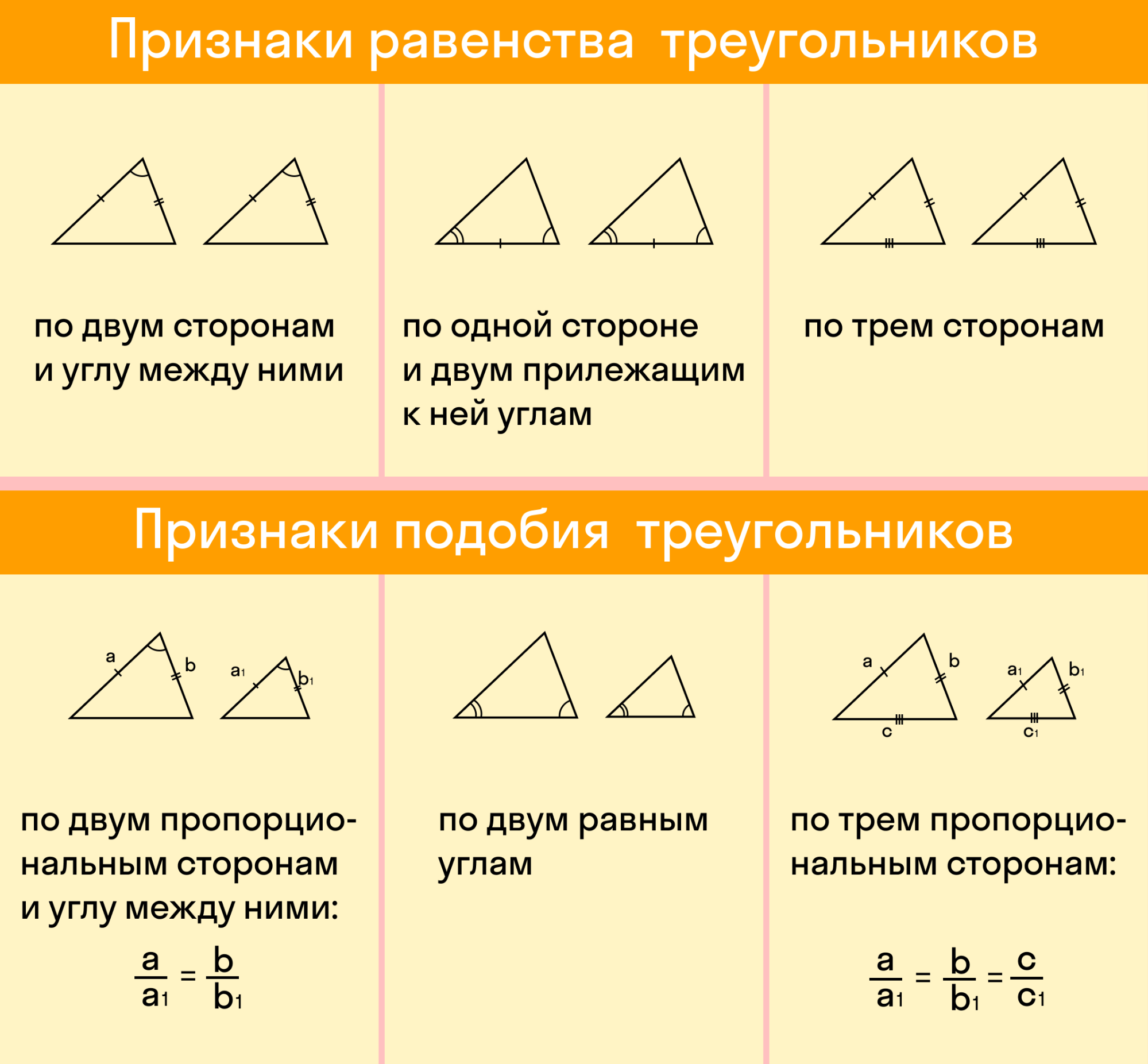
Первый признак равенства треугольников звучит так:
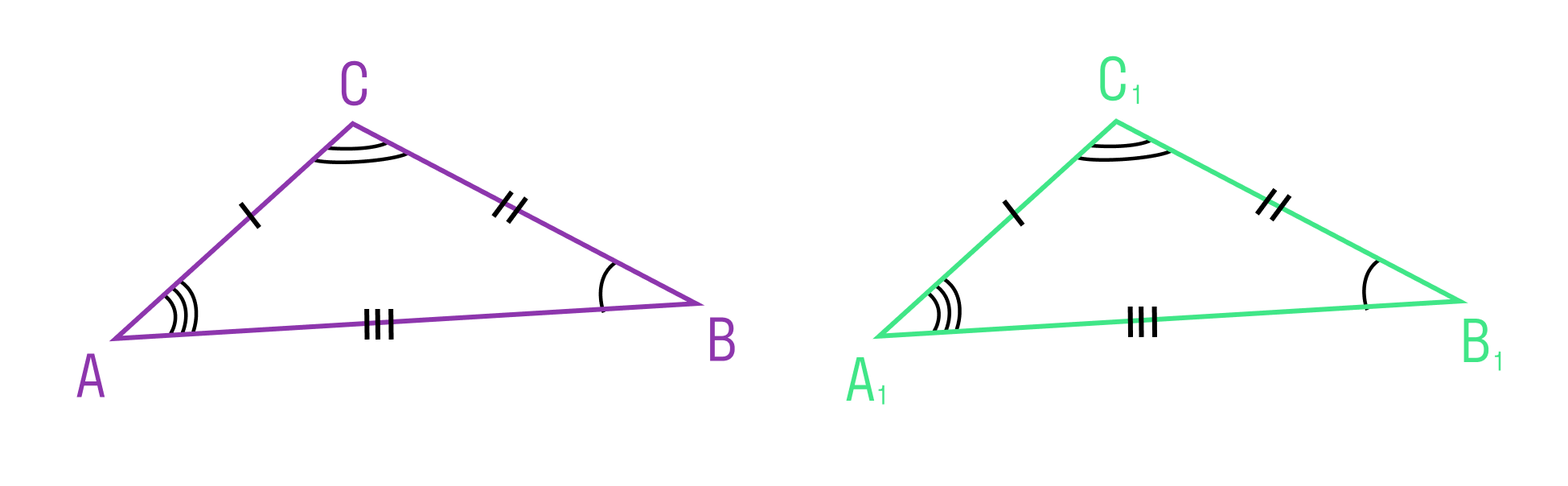
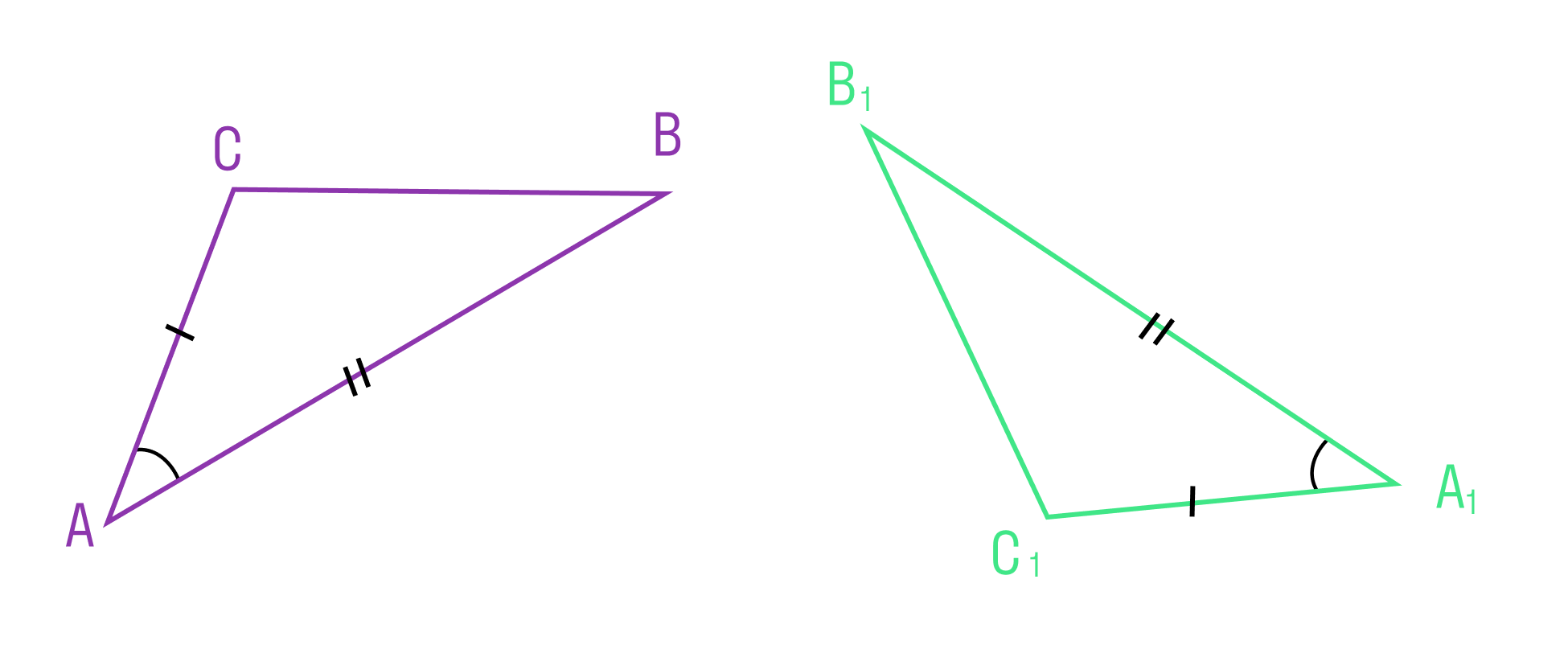
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Второй признак равенства треугольников
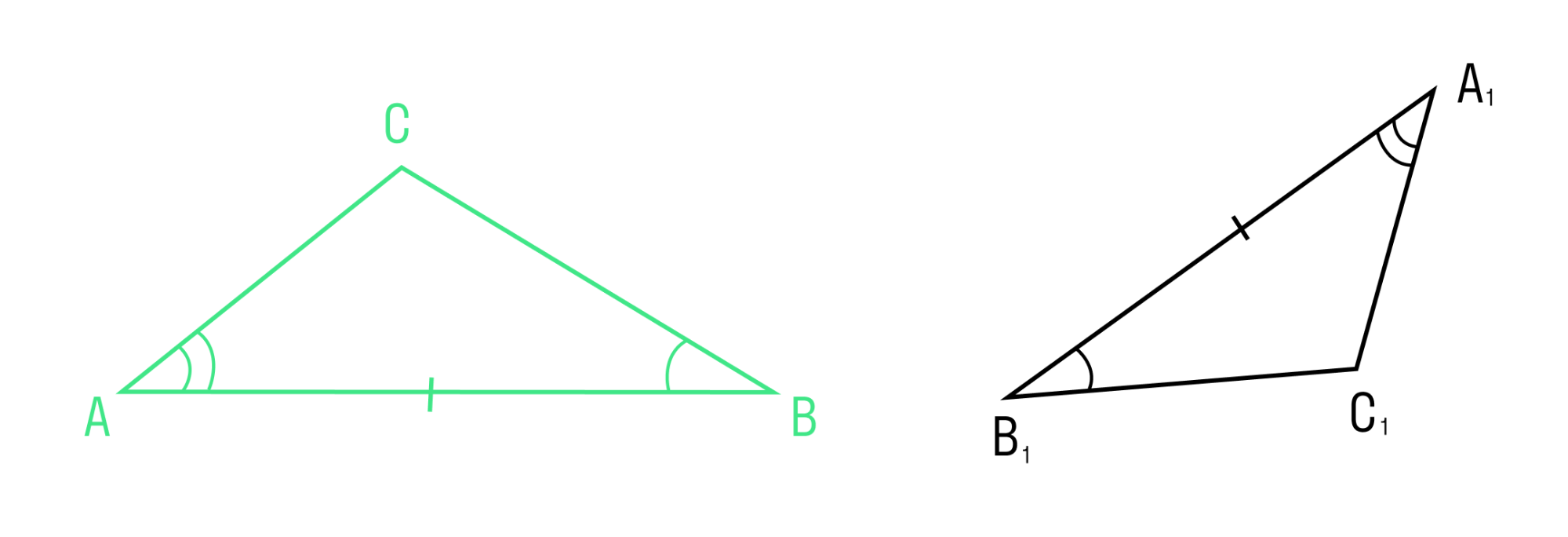
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников
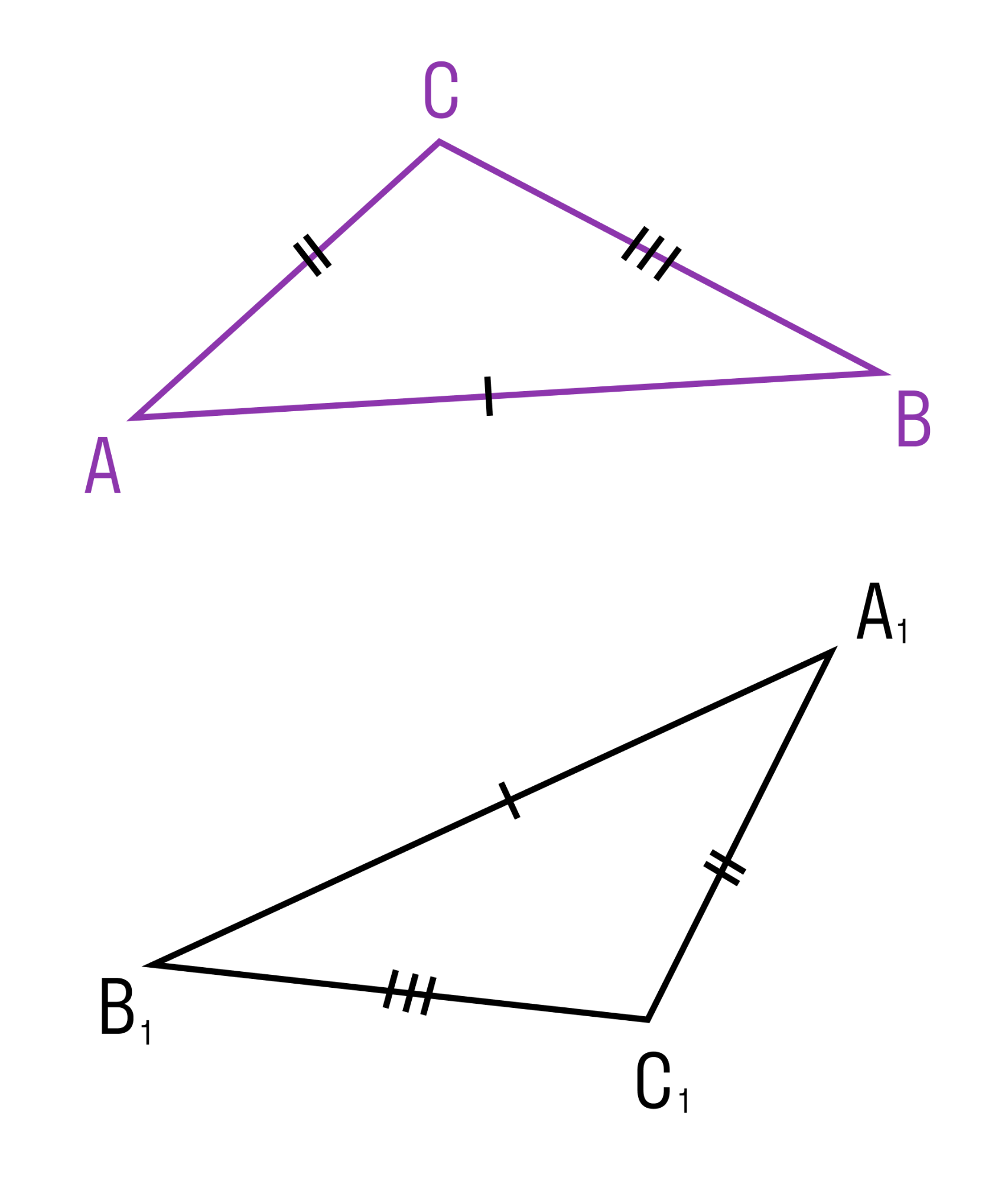
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
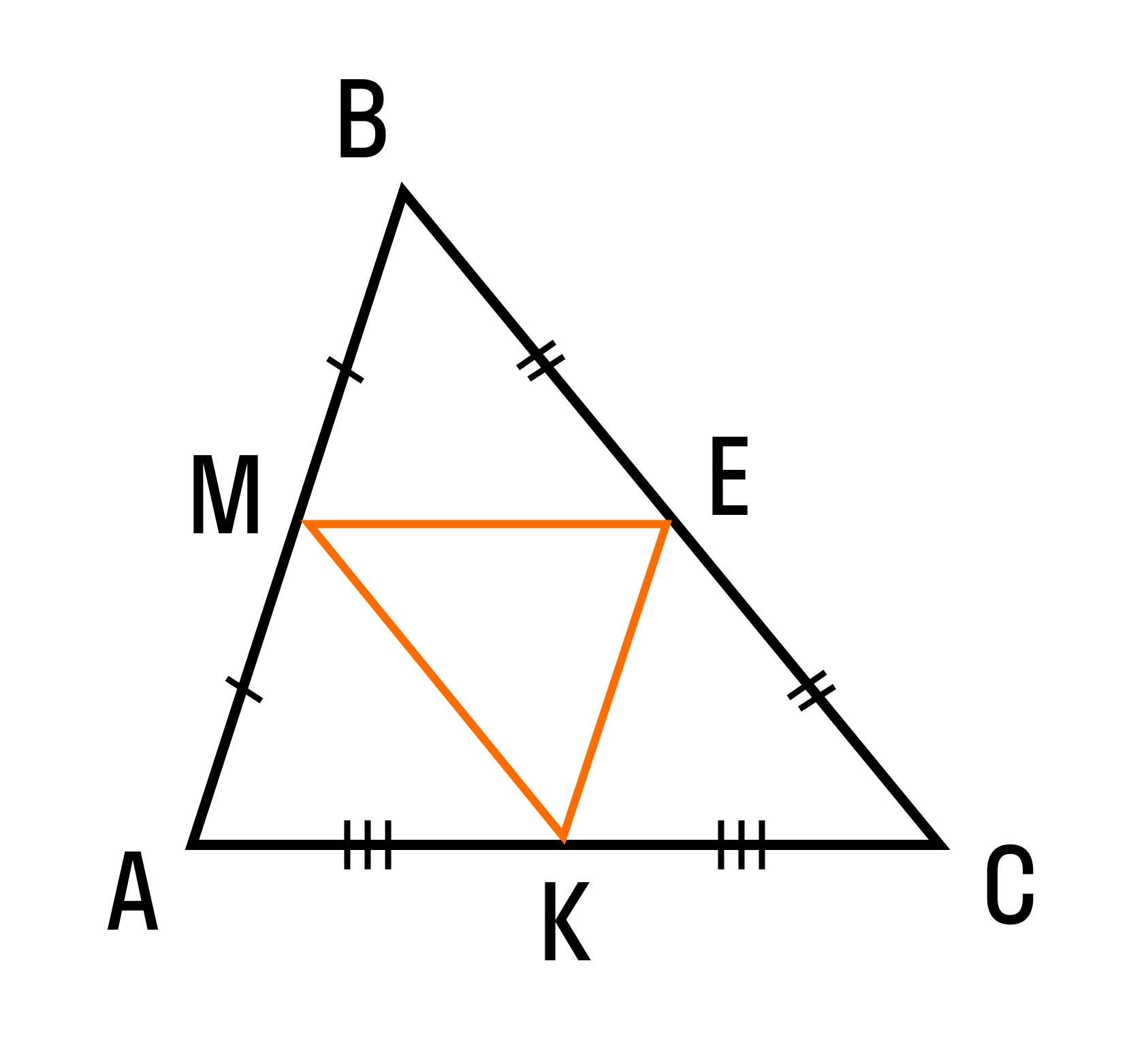
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
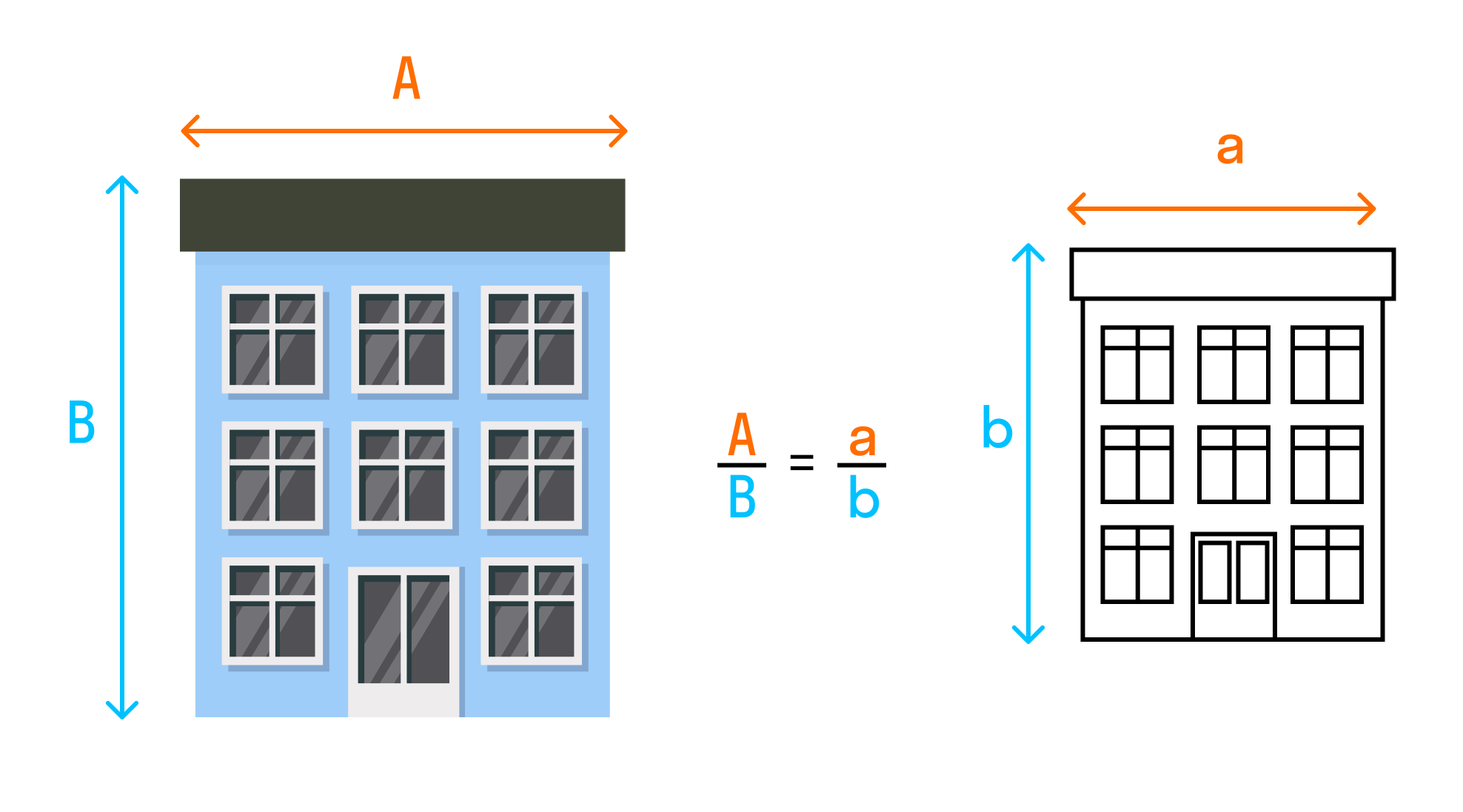
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
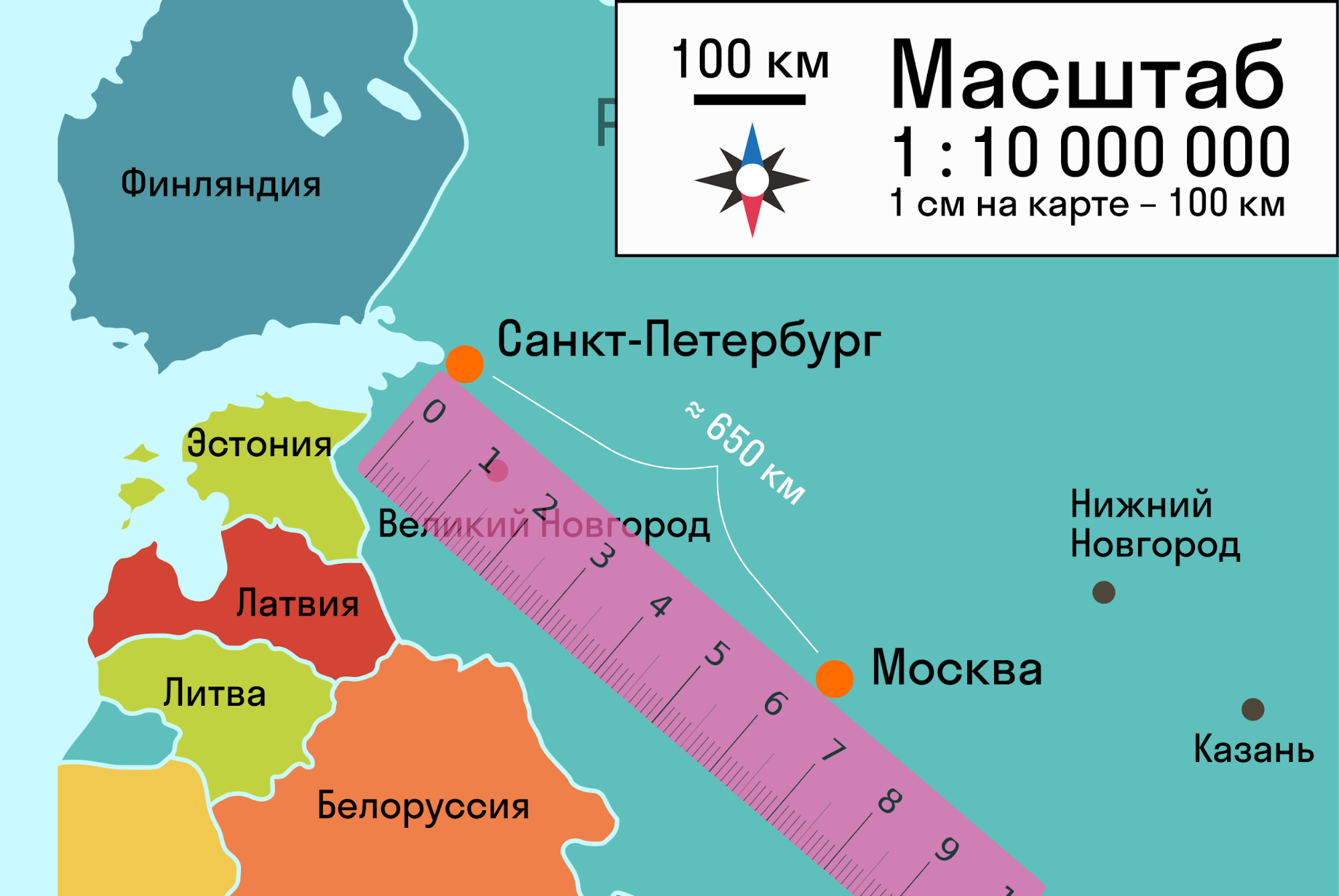
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
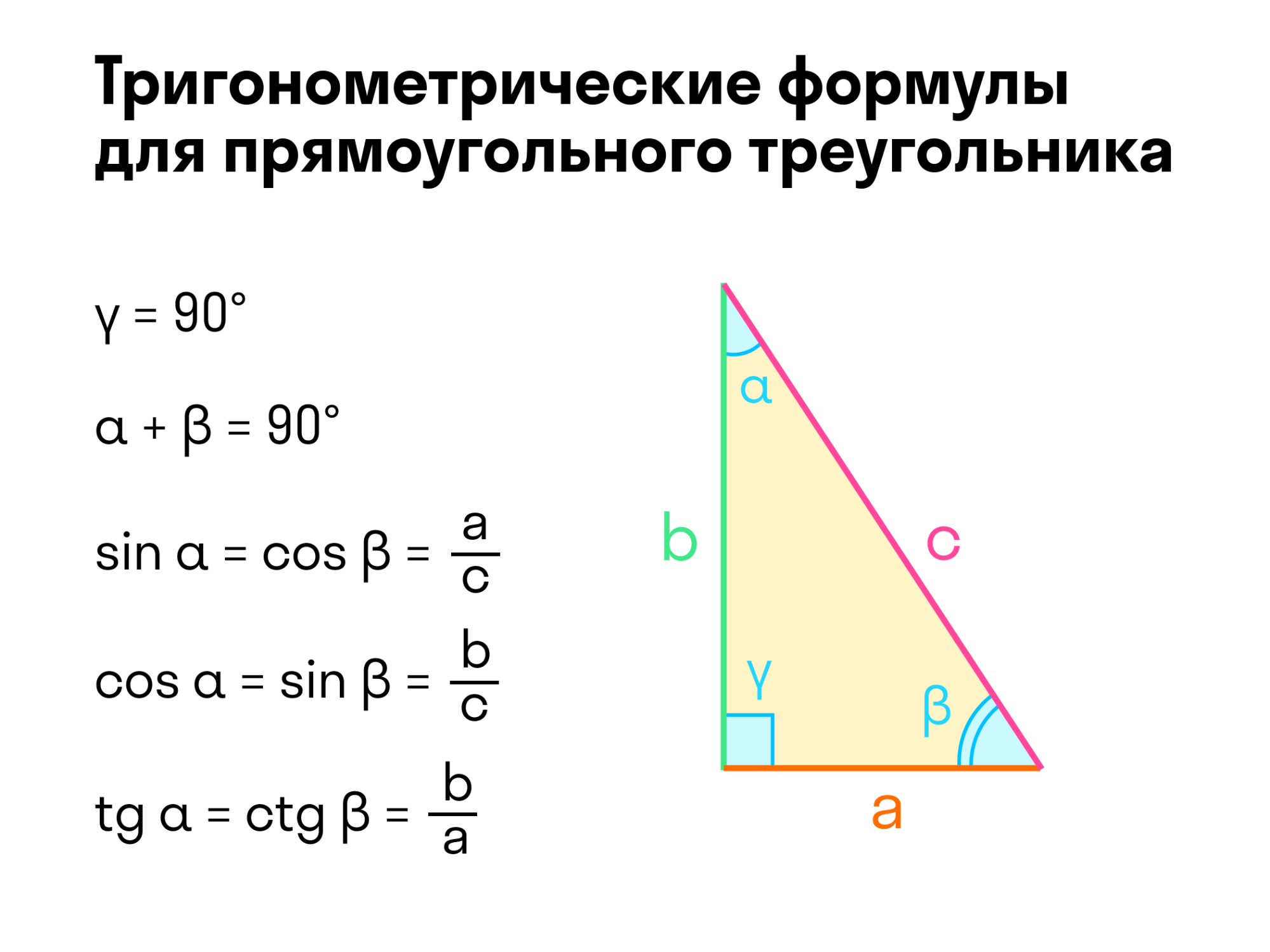
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
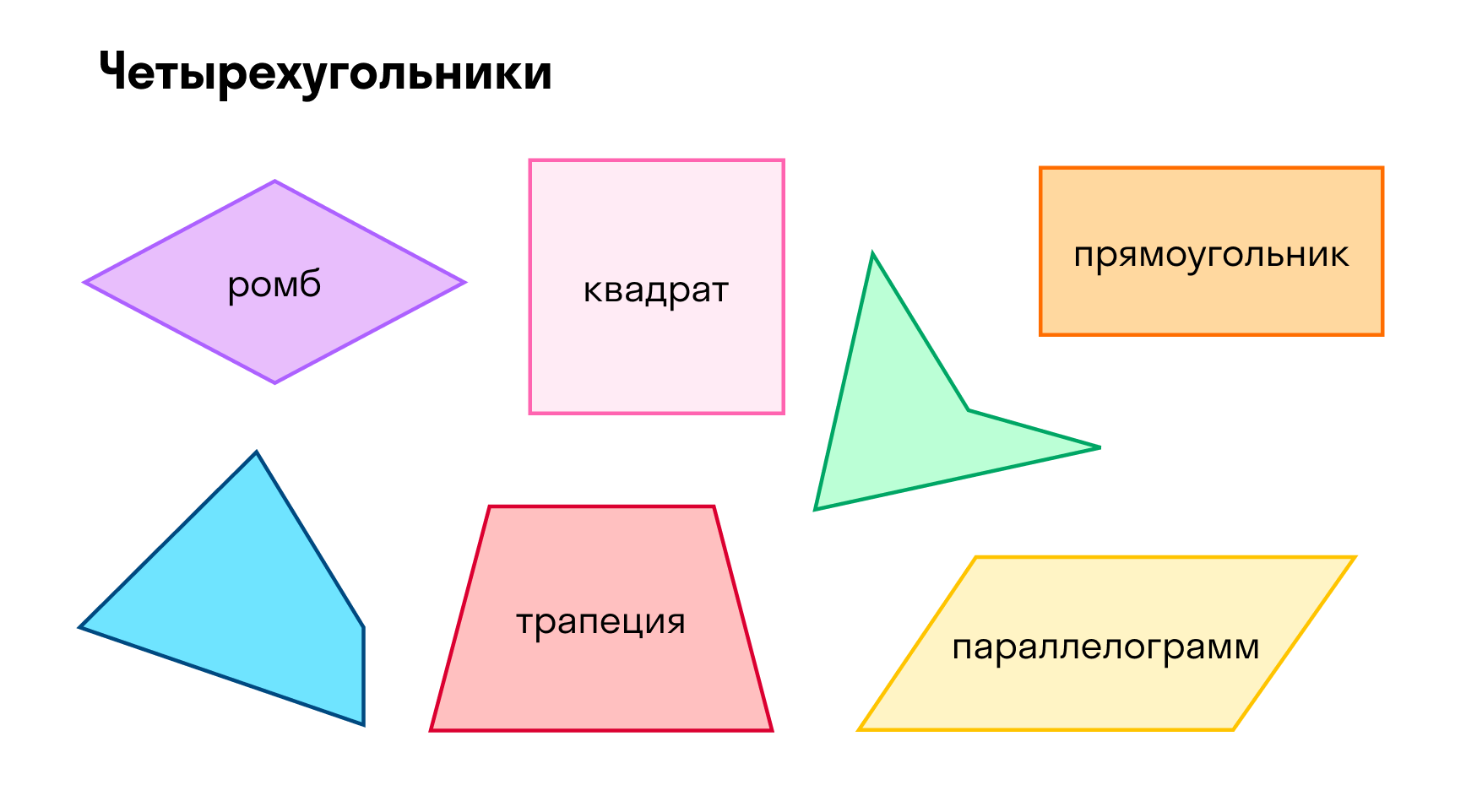
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
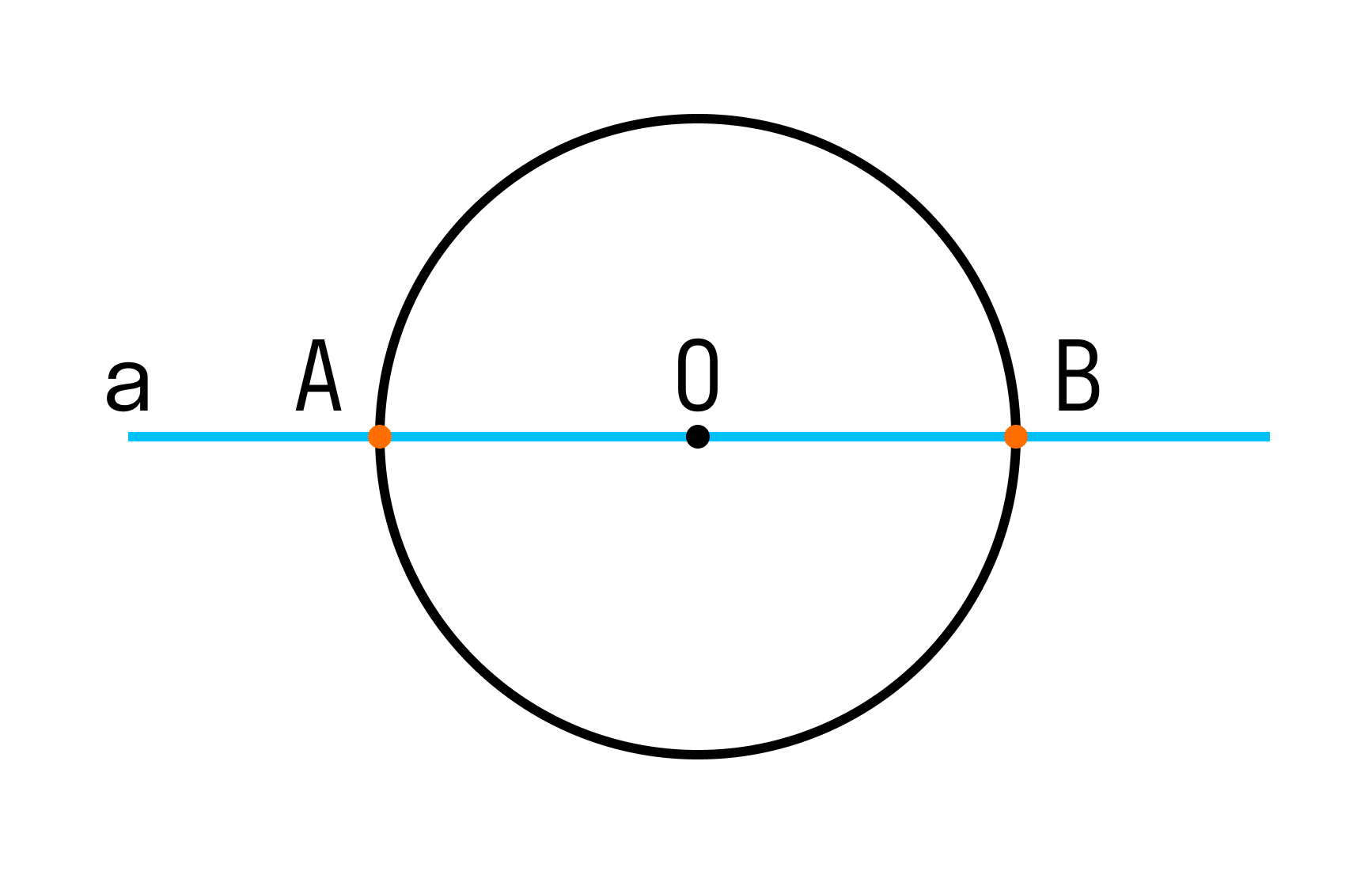
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
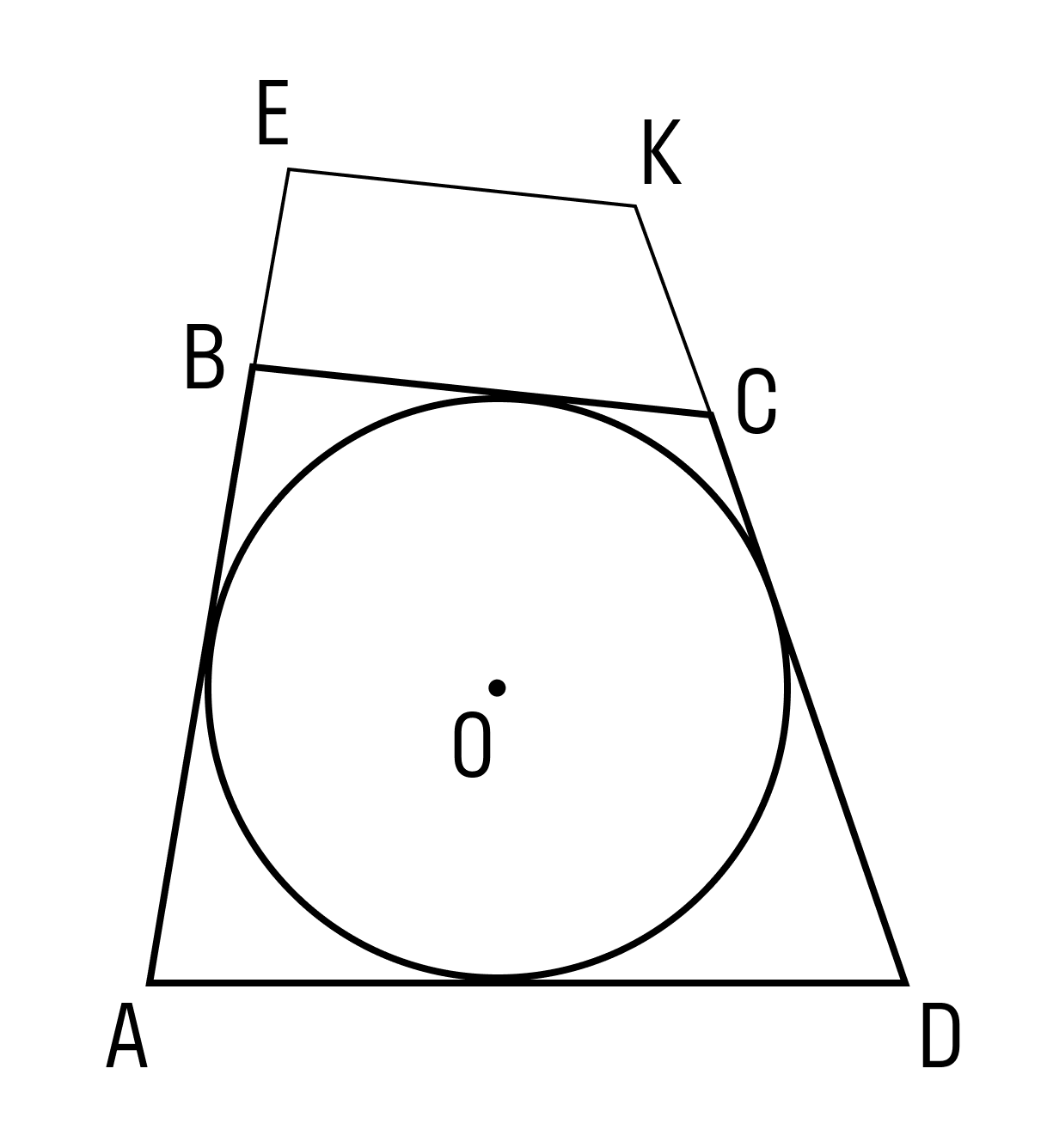
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
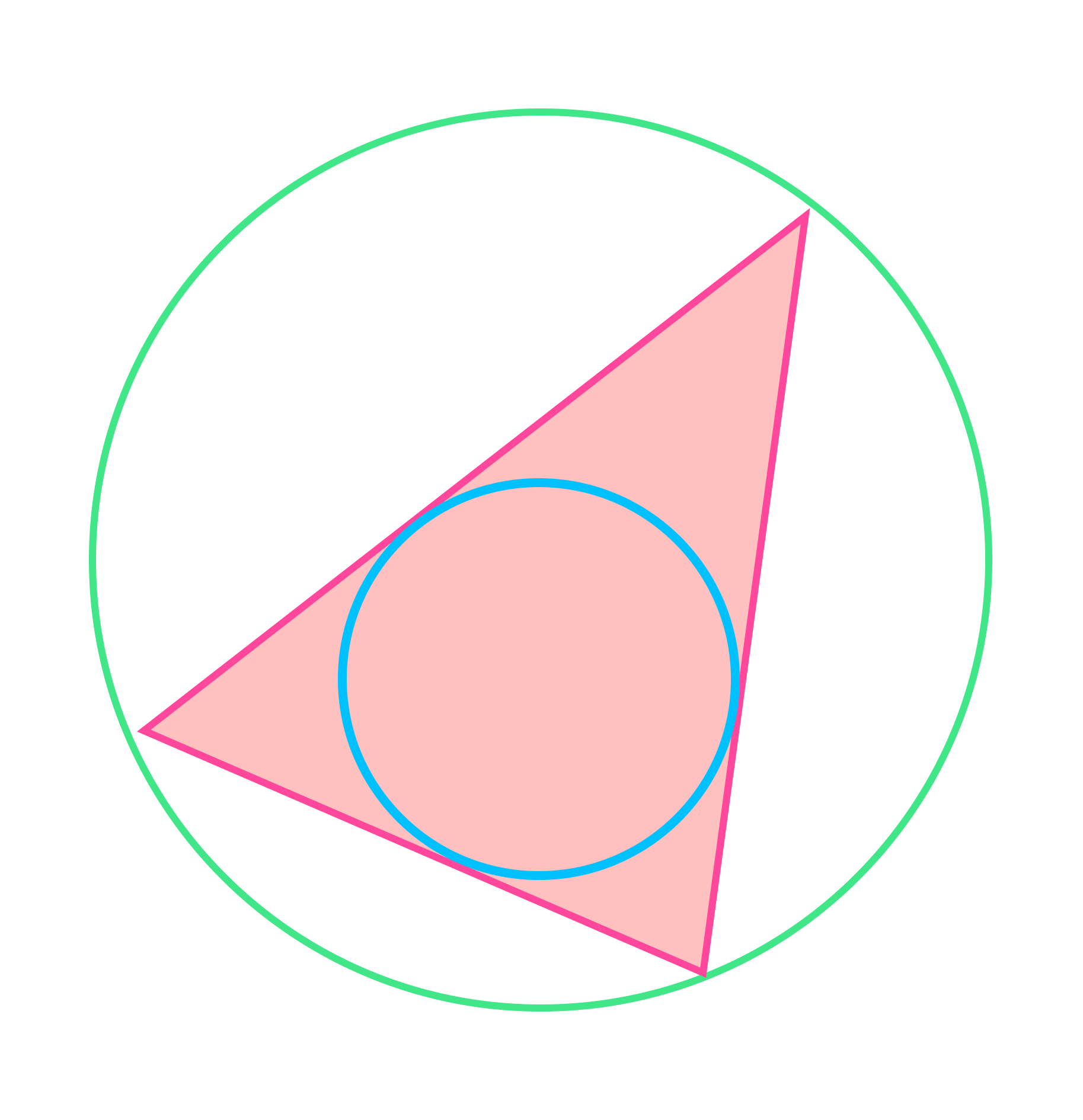
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Вот и настал момент прощания с математикой, сопровождающей нас на протяжении долгих шести лет школьной жизни. Но огорчаться не нужно, на смену привычной математике приходят занимательные и интересные разделы этой науки – алгебра и геометрия.
Давайте разберемся, что же такое геометрия, для чего она нужна, где её используют?
В дословном переводе с греческого, геометрия означает землемерие:
Геометрия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.
Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основе инвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.
Аксиома — математическое предложение, принимаемое без доказательства, называют аксиомой.
Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости.
Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.
Проективная геометрия — изучающая проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях.
Аффинная геометрия — изучающая свойства фигур, сохраняющиеся при аффинных преобразованиях.
Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.
Прямая линия, ограниченная с одного конца и неограниченная с другого, называется лучом.
Угол — это геометрическая фигура, образованная двумя лучами (стороны угла), исходящими из одной точки (вершина угла). Применяются две единицы измерения углов: радиан и градус. Угол в 90° называется прямым; угол, меньший чем 90°, называется острым; угол, больший чем 90°, называется тупым.
Смежные углы — это углы, имеющие общую вершину и общую сторону; две другие стороны являются продолжениями одна другой. Сумма смежных углов равна 180°. Вертикальные углы — это два угла с общей вершиной, у которых стороны одного являются продолжениями сторон другого.
Биссектрисой угла — называется луч, делящий угол пополам.
Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Все прямые, параллельные одной прямой, параллельны между собой. Все перпендикуляры к одной и той же прямой параллельны между собой, и обратно, прямая, перпендикулярная к одной из параллельных прямых, перпендикулярна к остальным. Длина отрезка перпендикуляра, заключенного между двумя параллельными прямыми, есть расстояние между ними. При пересечении двух параллельных прямых третьей прямой образуются восемь углов, которые попарно называются: соответственные углы (эти углы попарно равны); внутренние накрест лежащие углы (они попарно равны); внешние накрест лежащие углы (они попарно равны); внутренние односторонние углы (их сумма равна 180°); внешние односторонние углы (их сумма равна 180°).
Теорема Фалеса. При пересечении сторон угла параллельными прямыми стороны угла делятся на пропорциональные отрезки.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение.
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
Линия — представляет собой массу точек. Линии принято обозначать строчными буквами латиницы.
С углами, отрезками и методом сравнения без использования вычислений мы познакомились. Теперь давайте узнаем, какие бывают виды углов в зависимости от градусной меры.
Острый. Градусная мера 90 ˚
Развернутый. Градусная мера =180 ˚. Развернутый угол, состоит из двух прямых углов.
Когда углы дополняют один другого, то они могут быть смежными углами и вертикальными углами.
Смежные углы – углы, у которых есть общая сторона, а из оставшихся сторон получается прямая линия.
Если прямые никогда не пересекаются на плоскости, то их называют параллельными.
Аксиома принадлежности — через любые две точки на плоскости можно провести прямую и притом только одну. Аксиома порядка: среди любых трех точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.
Aксиома конгруэнтности (равенства) отрезков и углов —если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой. Аксиома параллельных прямых: через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
Аксиома непрерывности (аксиома Архимеда): для любых двух отрезков AB и CD существует конечный набор точек A1, A2, …, An, лежащих на прямой AB, таких что отрезки AA1, A1A2, …, An-1An конгруэнтны отрезку CD, a точка B лежит между A и An.
Плоская фигура, образованная замкнутой цепочкой отрезков, называется многоугольником.
В зависимости от количества углов многоугольник может быть треугольником, четырехугольником, пятиугольником, шестиугольником и т. д. Сумма длин называется периметром и обозначается p.
Если все диагонали лежат внутри многоугольника, он называется выпуклым. Сумма внутренних углов выпуклого многоугольника равна 180°*(n—2), где n — число углов (или сторон) многоугольника.
Треугольник — это многоугольник с тремя сторонами (или тремя углами). Если все три угла острые, то это остроугольный треугольник. Если один из углов прямой, то это прямоугольный треугольник; стороны, образующие прямой угол, называются катетами; сторона, противоположная прямому углу, называется гипотенузой. Если один из углов тупой, то это тупоугольный треугольник. Треугольник равнобедренный, если две его стороны равны. Треугольник равносторонний, если все его стороны равны.
В прямоугольном треугольнике справедливы следующие соотношения:
Площадь прямоугольного треугольника :
Радиус вписанной окружности:
В произвольном треугольнике:
В любой правильный многоугольник можно вписать окружность и около него можно описать окружность:
Площадь правильного многоугольника:
Длины сторон и диагоналей связаны формулой:
Основные свойства треугольников:
Признаки равенства треугольников: треугольники равны, если равны:
Признаки равенства прямоугольных треугольников: два прямоугольных треугольника равны, если выполняется одно из следующих условий:
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или ее продолжение). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника расположен внутри треугольника, а ортоцентр тупоугольного треугольника — снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
Формула для высоты треугольника:
Медиана — это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
Биссектриса — это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанного круга. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.
Формула для биссектрисы треугольника:
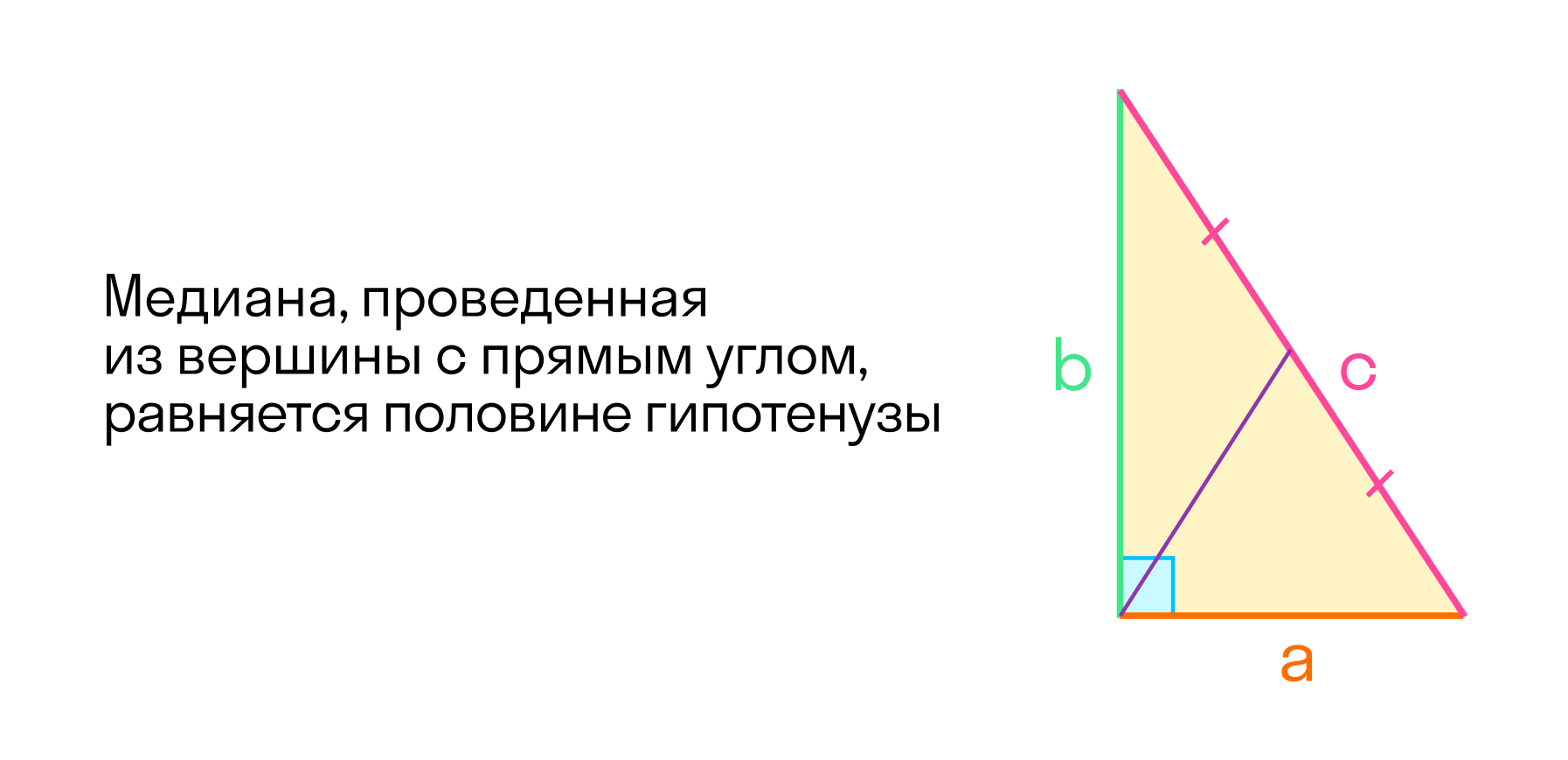
Срединный перпендикуляр — это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга. В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном — снаружи; в прямоугольном — в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.
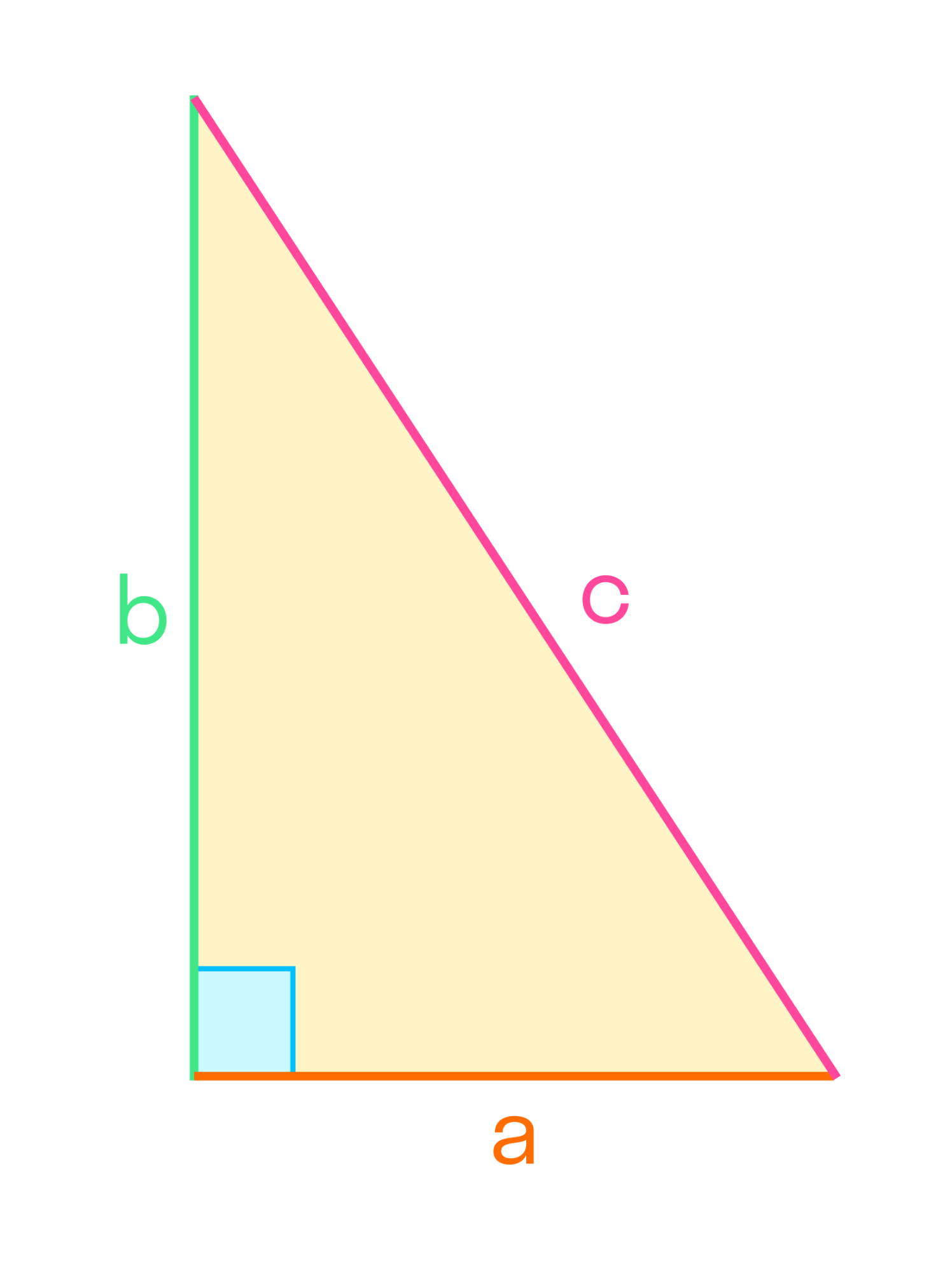
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов: c2 = a2 + b2.
В общем случае (для произвольного треугольника) имеем: c2=a2+b2–2?a?b?cosC, где C — угол между сторонами a и b.
Четырехугольник — фигура, образованная четырьмя точками (вершинами), никакие три из которых не лежат на одной прямой, и четырьмя последовательно соединяющими их отрезками (сторонами), которые не должны пересекаться.
Параллелограмм — это четырехугольник, противоположные стороны которого попарно параллельны. Любые две противоположные стороны параллелограмма называются его основаниями, а расстояние между ними — высотой.
Радиус вписанной в параллелограмм окружности:
Прямоугольник — это параллелограмм, все углы которого равны 90°.
Основные свойства прямоугольника.
Стороны прямоугольника являются одновременно его высотами.
Диагонали прямоугольника равны: AC = BD.
Квадрат диагонали прямоугольника равен сумме квадратов его сторон (по теореме Пифагора).
Площадь прямоугольника:S = ab.
Радиус описанной около прямоугольника окружности:
Ромбом называется параллелограмм, у которого все стороны равны. Диагонали ромба взаимно перпендикулярны и делят их углы пополам.
Площадь ромба выражается через диагонали:
Квадрат — это параллелограмм с прямыми углами и равными сторонами. Квадрат является частным случаем прямоугольника и ромба одновременно, следовательно, он обладает всеми их вышеперечисленными свойствами.
Радиус описанной около квадрата окружности:
Радиус вписанной в квадрат окружности:
Трапеция — это четырехугольник, у которого две противоположные стороны параллельны. Параллельные стороны называюся основаниями трапеции, а две другие — боковыми сторонами. Расстояние между основаниями есть высота. Отрезок, соединяющий средние точки боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований и параллельна им. Трапеция с равными боковыми сторонами называется равнобочной трапецией. В равнобочной трапеции углы при каждом основании равны.
Средняя линия треугольника — это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине его основания и параллельна ему. Это свойство вытекает из свойства трапеции, так как треугольник может рассматриваться как случай вырождения трапеции, когда одно из ее оснований превращается в точку.
Подобие плоских фигур. Если изменить все размеры плоской фигуры одно и то же число раз (отношение подобия), то старая и новая фигуры называются подобными. Два многоугольника подобны, если их углы равны, а стороны пропорциональны.
Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон, диаметров).
Геометрическое место точек — это множество всех точек, удовлетворяющих определенным заданным условиям.
Окружность — это геометрическое место точек на плоскости, равноудаленных от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается — r. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности называется дугой. Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности — хордой. Хорда, проходящая через центр круга, называется диаметром и обозначается d. Диаметр — это наибольшая хорда, по величине равная двум радиусам: d = 2r.
Сегмент — это часть круга, ограниченная дугой и соответствующей хордой. Длина перпендикуляра, проведенного из середины хорды до пересечения с дугой, называется высотой сегмента.
Сектор — это часть круга, ограниченная дугой и двумя радиусами, проведенными к концам этой дуги.
Центральный угол — угол, образованный двумя радиусами. Вписанный угол — это угол, образованный двумя хордами, проведенными из их одной общей точки. Описанный угол — угол, образованный двумя касательными, проведенными из одной общей точки.
Радианная мера любого угла — это отношение длины дуги, проведенной произвольным радиусом и заключенной между сторонами этого угла, к ее радиусу.
Соотношения между элементами круга.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Следовательно, все вписанные углы, опирающиеся на одну и ту же дугу, равны. А так как центральный угол содержит то же количество градусов, что и его дуга, то любой вписанный угол измеряется половиной дуги, на которую он опирается.
Все вписанные углы, опирающиеся на полукруг, прямые.
Угол, образованный двумя хордами, измеряется полусуммой дуг, заключенных между его сторонами.
Угол, образованный двумя секущими, измеряется полуразностью дуг, заключенных между его сторонами.
Угол, образованный касательной и хордой, измеряется половиной дуги, заключенной внутри него.
Угол, образованный касательной и секущей, измеряется полуразностью дуг, заключенных между его сторонами.
Описанный угол, образованный двумя касательными, измеряется полуразностью дуг, заключенных между его сторонами.
Произведения отрезков хорд, на которые они делятся точкой пересечения, равны.
Квадрат касательной равен произведению секущей на ее внешнюю часть.
Хорда, перпендикулярная диаметру, делится в их точке пересечения пополам.
Вписанным в круг называется многоугольник, вершины которого расположены на окружности. Описанным около круга называется многоугольник, стороны которого являются касательными к окружности. Соответственно, окружность, проходящая через вершины многоугольника, называется описанной около многоугольника; окружность, для которой стороны многоугольника являются касательными, называется вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника эта возможность существует всегда.
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба (квадрата). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырехугольника можно описать круг, если сумма его противоположных углов равна 180°. Для параллелограммов это возможно только для прямоугольника (квадрата). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, если только она равнобочная. Правильный многоугольник — это многоугольник с равными сторонами и углами.
Основные аксиомы стереометрии.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Если две различные прямые имеют общую точку, то через них можно провести одну и только одну плоскость.
Через три точки, лежащие на одной прямой, можно провести бесчисленное множество плоскостей, образующих в этом случае пучок плоскостей. Прямая, через которую проходят все плоскости пучка, называется осью пучка. Через любую прямую и точку, лежащую вне этой прямой, можно провести одну и только одну плоскость. Через две прямые не всегда можно провести плоскость, тогда эти прямые называются скрещивающимися.
Скрещивающиеся прямые не пересекаются, сколько бы их ни продолжать, но они не являются параллельными прямыми, так как не лежат в одной плоскости. Только параллельные прямые являются непересекающимися линиями, через которые можно провести плоскость. Разница между скрещивающимися и параллельными прямыми состоит в том, что параллельные прямые имеют одинаковое направление, а скрещивающиеся — нет. Через две пересекающиеся прямые всегда можно провести одну и только одну плоскость. Расстояние между двумя скрещивающимися прямыми есть длина отрезка, соединяющего ближайшие точки, расположенные на скрещивающихся прямых. Непересекающиеся плоскости называются параллельными плоскостями. Плоскость и прямая либо пересекаются (в одной точке), либо нет. В последнем случае говорят, что прямая и плоскость параллельны друг другу.
Перпендикуляром, опущенным из точки на плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и ежащей на прямой, перпендикулярной плоскости.
Проекцией точки на плоскость называется основание перпендикуляра, опущенного из точки на плоскость. Проекцией отрезка на плоскость P является отрезок, концы которого являются проекциями точек данного отрезка.
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая их прямая — ребром двугранного угла. Плоскость, перпендикулярная к ребру, дает в ее пересечении с полуплоскостями угол называемый линейным углом двугранного угла. Двугранный угол измеряется своим линейным углом.
Многогранный угол. Если через точку провести множество плоскостей, которые последовательно пересекаются друг с другом по прямым, то получим фигуру, называемую многогранным углом. Плоскости, образующие многогранный угол называются его гранями; прямые, по которым последовательно пересекаются грани называются ребрами многогранного угла. Минимальное количество граней многогранного угла равно трем.
Параллельные плоскости вырезают на ребрах многогранного угла, пропорциональные отрезки и образуют подобные многоугольники.
Признаки параллельности прямой и плоскости.
Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Признаки параллельности плоскостей:
Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости.
Теорема о трех перпендикулярах
Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.
Признаки параллельности прямых в пространстве:
Уравнение прямой на плоскости в прямоугольной системе координат xy:
ax + bx + c = 0, где a, b, c — постоянные числа, x и y —координаты переменной точки M(x,y) на прямой.
Признаки параллельности прямых:
Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.
Многогранник — это тело, граница которого состоит из кусков плоскостей (многоугольников). Эти многоугольники называются гранями, их стороны — ребрами, их вершины — вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник — выпуклый, если все его диагонали расположены внутри него.
Куб — объемная фигура с шестью равными гранями.
Объем и площадь поверхности куба:
Призмой называется многогранник, две грани которого (основания призмы) — равные многоугольники с соответственно параллельными сторонами, а остальные грани — параллелограммы.
Отрезки, соединяющие соответствующие вершины, называются боковыми ребрами. Высота призмы — это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть, соответственно треугольной, четырёхугольной, пятиугольной, шестиугольной и т. д. Если боковые ребра призмы перпендикулярны к плоскости основания, то такая призма называется прямой; в противном случае это наклонная призма. Если в основании прямой призмы лежит правильный многоугольник, то такая призма также называется правильной. Диагональю призмы называется отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Площадь боковой поверхности прямой призмы:
Sбок = P*H, где P — периметр основания, а H — высота.
Параллелепипед — это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней, и все они — параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам.
Если четыре боковые грани параллелепипеда — прямоугольники, то он называется прямым. Прямой параллелепипед, у которого все шесть граней — прямоугольники, называется прямоугольным. Диагональ прямоугольного параллелепипеда d и его ребра a, b, c связаны соотношением d2 = a2 + b2 + c2. Прямоугольный параллелепипед, все грани которого квадраты, называется кубом. Все ребра куба равны.
Объем и площадь поверхности прямоугольного параллелепипеда:
V = a*b*c, Sполн = 2(ab + ac + bc).
Пирамида — это многогранник, у которого одна грань (основание пирамиды) является произвольным многоугольником, а остальные грани (боковые грани) — треугольники с общей вершиной, называемой вершиной пирамиды. Перпендикуляр, опущенный из вершины пирамиды на ее основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть, соответственно, треугольной, четырехугольной, пятиугольной, шестиугольной и т. д. Треугольная пирамида является тетраэдром, четырехугольная — пятигранником и т. д. Пирамида называется правильной, если в основании лежит правильный многоугольник, а ее высота падает в центр основания. Все боковые ребра правильной пирамиды равны; все боковые грани — равнобедренные треугольники. Высота боковой грани называется апофемой правильной пирамиды.
Если провести сечение, параллельное основанию пирамиды, то тело, заключенное между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани называются основаниями; расстояние между ними — высотой. Усеченная пирамида называется правильной, если пирамида, из которой она была получена, — правильная. Все боковые грани правильной усеченной пирамиды — равные равнобочные трапеции.
Площадь боковой поверхности правильной пирамиды:
Объем усеченной пирамиды:
Площадь боковой поверхности правильной усеченной пирамиды:
Цилиндрическая поверхность образуется при движении прямой, сохраняющей свое направление и пересекающейся с заданной линией (кривой). Эта линия называется направляющей. Прямые, соответствующие различным положениям прямой при ее движении, называются образующими цилиндрической поверхности.
Цилиндром называется тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Части этих плоскостей называются основаниями цилиндра. Расстояние между основаниями — высота цилиндра. Цилиндр прямой, если его образующие перпендикулярны основанию; в противном случае цилиндр наклонный. Цилиндр называется круговым, если его основание — круг. Если цилиндр является одновременно и прямым, и круговым, то он называется круглым. Призма является частным случаем цилиндра.
Объем, площади боковой и полной поверхностей цилиндра:
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, параллельные основанию, — круги того же радиуса.
Сечения, параллельные образующим цилиндра, — пары параллельных прямых.
Сечения, которые не параллельны ни основанию, ни образующим, — эллипсы.
Коническая поверхность образуется при движении прямой, проходящей все время через неподвижную точку, и пересекающей за данную линию, называемую направляющей. Прямые, соответствующие различным положениям прямой при ее движении, называются образующими конической поверхности; точка — ее вершиной. Коническая поверхность состоит из двух частей: одна описывается лучом, другая — его продолжением.
Обычно в качестве конической поверхности рассматривают одну из её частей.
Конус — это тело, ограниченное одной из частей конической поверхности с замкнутой направляющей и пересекающей коническую поверхность плоскостью, не проходящей через вершину.
Часть этой плоскости, расположенной внутри конической поверхности, называется основанием конуса. Перпендикуляр, опущенный из вершины на основание, называется высотой конуса.
Пирамида является частным случаем конуса. Конус называется круговым, если его основанием является круг. Прямая, соединяющая вершину конуса с центром основания, называется осью конуса. Если высота кругового конуса совпадает с его осью, то такой конус называется круглым.
Объем, площади боковой и полной поверхностей конуса:
Объем и площадь боковой поверхности усеченного конуса:
Сечения кругового конуса, параллельные его основанию, — круги.
Сечение, пересекающее только одну часть кругового конуса и не параллельное ни одной его образующей, — эллипс.
Сечение, пересекающее только одну часть кругового конуса и параллельное одной из его образующих, — парабола.
Сечение, пересекающее обе части кругового конуса, в общем случае является гиперболой, состоящей из двух ветвей. В частности, если это сечение проходит через ось конуса, то получаем пару пересекающихся прямых (образующих конус).
Сферическая поверхность — это геометрическое место точек в пространстве, равноудаленных от одной точки, которая называется центром сферической поверхности.
Шар (сфера) — это тело, ограниченное сферической поверхностью. Можно получить шар, вращая полукруг (или круг) вокруг диаметра. Все плоские сечения шара — круги. Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра, можно провести бесчисленное множество больших кругов.
Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а поверхность шара в полтора раза меньше полной поверхности того же цилиндра.
Часть шара (сферы), отсекаемая от него какой-либо плоскостью, называется шаровым (сферическим) сегментом. Круг называется основанием шарового сегмента. Отрезок перпендикуляра, проведенного из центра круга до пересечения со сферической поверхностью, называется высотой шарового сегмента. Часть сферы, заключенная между двумя параллельными плоскостями, пересекающими сферическую поверхность, называется шаровым слоем; кривая поверхность шарового слоя называется шаровым поясом (зоной). Расстояние между основаниями шарового пояса — его высота. Часть шара, ограниченная кривой поверхностью сферического сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара, называется шаровым сектором.