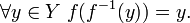Что такое образ функции

Понятие отображения (функции). Образы и прообразы множеств.

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Другими словами, функция — это правило, по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Элемент y=f(x), который сопоставлен элементу x, называется образом элемента (точки) x (при отображении f).

Если взять целиком подмножество A области определения функции f, то можно рассмотреть совокупность образов всех элементов множества A, а именно подмножество области значений (функции f) вида

которое, называется образом множества A (при отображении f). Это множество иногда обозначается как f[A] или A^f.

Наоборот, взяв некоторое подмножество B области значений функции f, можно рассмотреть совокупность тех элементов области определения (функции f), чьи образы попадают в множество B, а именно — множество вида которое называется (полным) прообразом множества B (при отображении f).

7. Способы задания функций. Обратная функция, сложная функция

· Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

· Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

· Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

· Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Чтобы найти обратную функцию, нужно решить уравнение y = f(x) относительно x. Если оно имеет более чем один корень, то функции обратной к f не существует. Таким образом, функция f(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она биективна.

Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).

Пусть функция g определена на множестве X и может принимать значения в множестве U. В таком случае говорят, что функция g отображает множество X в U, а сама функция записывается как

Представим теперь, что на множестве U задана другая функция f, которая отображает множество U в Y:

Такое двойное отображение, при котором область значений первого отображения является подмножеством области определения второго отображения, называется композицией отображений, а соответствующие функции образуют композицию функций.

Если g : X → U и f : U → Y, то композиция функций g и f обозначается как

и представляет собой «двухслойную» сложную функцию или функцию от функции.

8. Числовые последовательности.

Числовой последовательностью называется числовая функция, заданная на множестве натуральных чисел или на множестве первых натуральных чисел.

Для числовых последовательностей вместо обычно пишут , саму последовательность обозначают , общий член последовательности обозначают . Числа называются членами последовательности: — первый член последовательности, — второй член последовательности, — -ый член последовательности и т.д.

Числовая последовательность определена, если указан закон, по которому каждому натуральному числу ставиться в соответствие действительное число .

Числовая последовательность может быть определена заданием ее -го члена формулой, позволяющей найти любой член последовательности простой подстановкой номера искомого члена в эту формулу. Такой способ задания последовательности называется явным.

Закон образования числовой последовательности может состоять в задании нескольких первых членов последовательности и рекуррентной формулы, с помощью которой каждый следующий член выражается через предыдущий (или несколько предыдущих). Такой способ задания последовательности называется рекуррентным.

Числовая последовательность называется возрастающей, если в ней каждый следующий член больше предыдущего.

Числовая последовательность называется убывающей, если в ней каждый следующий член меньше предыдущего.

Числовая последовательность называется ограниченной, если существует такое натуральное число , что для любого натурального .

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Образ (математика)

В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.

Содержание

Определения

Обозначения

Связанные определения

Свойства

Свойства прообразов и образов

Классы функций

Вариации и обобщения

Функции нескольких аргументов

Определение функции легко обобщить на случай функции многих аргументов.

Примечания

См. также

Литература

Полезное

Смотреть что такое «Образ (математика)» в других словарях:

Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия

Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия

Путь (математика) — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия

Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия

Пучок (математика) — У этого термина существуют и другие значения, см. Пучок. Пучки используются для установления отношений между локальными и глобальными данными. По этой причине они играют значительную роль в топологии, дифференциальной геометрии и алгебраической… … Википедия

Хиральность (математика) — У этого термина существуют и другие значения, см. Хиральность (значения). В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с… … Википедия

Область (математика) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Промежуток (математика) — Промежуток, или более точно, промежуток числовой прямой множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними[1]. С использованием логических символов, это определение… … Википедия

Схема (математика) — В алгебраической геометрии схема это абстракция, позволяющая связать единым образом коммутативную алгебру и дифференциальную геометрию и переносить идеи из одной области в другую. В первую очередь понятие схемы позволяет перенести… … Википедия

Источник

Образ и прообраз при отображении

Взятие образа

Положим, и — подмножества области определения. Взятие образа (или, что то же самое, применение оператора ) обладает следующими свойствами:

· ;

· ;

· .

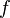
· образ объединения равен объединению образов: ;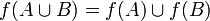

· образ пересечения является подмножеством пересечения образов .

Последние два свойства, вообще говоря, допускают обобщение на любое количество множеств, большее двух (как оно здесь сформулировано).

15. Определение прообраза подмножества относительно функции. Теорема о прообразе объединения и пересечения подмножеств относительно отображения.

Взятие прообраза

Положим, и — подмножества множества .

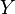
По аналогии с взятием образа, взятие прообраза (переход к прообразу) обладает также следующими двумя очевидными свойствами:

· прообраз объединения равен объединению прообразов: ;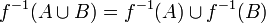

· прообраз пересечения равен пересечению прообразов .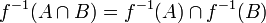

Данные свойства, также, допускают обобщение на любое количество множеств, большее двух (как оно здесь сформулировано).

В случае, если отображение обратимо (см. ниже), прообраз каждой точки области значений одноточечный, поэтому для обратимых отображений выполняется следующее усиленное свойство для пересечений:

· образ пересечения равен пересечению образов: .

16. Определение образа и прообраза подмножества относительно функции. Теоремы об образе прообраза и прообразе образа подмножества относительно функции.

Образ и прообраз (при отображении)

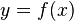
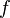
Элемент , который сопоставлен элементу , называется образом элемента (точки) (при отображении ).

Если взять целое подмножество области определения функции , то можно рассмотреть совокупность образов всех элементов множества , а именно подмножество области значений (функции ) вида

,

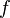
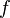
которое, называется образом множества (при отображении ). Это множество иногда обозначается как или .

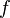
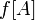
Наоборот, взяв некоторое подмножество области значений функции , можно рассмотреть совокупность тех элементов области определения (функции ), чьи образы попадают в множество , а именно — множество вида

,

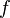
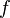
которое называется (полным) прообразом множества (при отображении ).

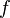
В том частном случае, когда множество состоит из одного элемента, скажем, , множество имеет более простое обозначение .

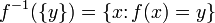
17. Свойства отображения – быть инъекцией, сюръекцией и биекцией. Теорема о композиции инъекций.

Инъективность

Основная статья: Инъекция (математика)

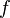
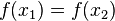
Функция называется инъективной (или, коротко, инъекция), если разным элементам множества сопоставлены разные элементы множества . Более формально, функция инъективна, если для любых двух элементов таких, что , непременно выполняется .

Другими словами, сюръекция — это когда «у каждого образа есть прообраз», а инъекция — это когда «разные — в разные». То есть при инъекции не бывает так, чтобы два или больше разных элементов отображались в один и тот же элемент . А при сюръекции не бывает так, чтобы какой-то элемент не имел прообраза.

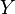
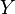
18. Свойства отображения – быть инъекцией, сюръекцией и биекцией. Теорема о композиции сюръекций.

Сюръективность

Основная статья: Сюръекция

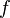
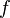
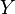
Функция называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция сюръективна, если образ множества при отображении совпадает с множеством : .

Такое отображение называется ещё отображением на.

Если условие сюръективности нарушается, то такое отображение называют отображением в.

Биекция

Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.

Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы.

Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества).

Определение

Функция называется биекцией (и обозначается ), если она:

1. Переводит разные элементы множества в разные элементы множества (инъективность). Иными словами,

· .

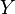
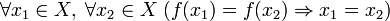
2. Любой элемент из 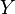имеет свой прообраз (сюръективность). Иными словами,

· .

Примеры

· Тождественное отображение на множестве биективно.

· — биективные функции из в себя. Вообще, любой моном одной переменной нечетной степени является биекцией из в себя.

· — биективная функция из в .

· не является биективной функцией, если считать её определённой на всём .

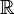
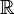
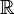
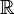
Свойства

· Функция является биективной тогда и только тогда, когда существует обратная функция такая, что

и

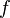
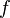
· Если функции и биективны, то и композиция функций биективна, в этом случае . Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если биективна, то мы можем утверждать лишь, что инъективна, а сюръективна.

20. Понятие о равномощности множеств. Счетные множества. Теорема о счетности или конечности объединения счетного числа конечных множеств. Пример применения теоремы к доказательству счетности множества всех слов над конечным алфавитом.

Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности.

21. Понятие о равномощности множеств. Счетные множества. Теорема о счетности счетного объединения счетных или конечных множеств. Пример применения теоремы к доказательству счетности множества всех конечных подмножеств в множестве всех слов над конечным алфавитом.

22. Понятие о равномощности множеств. Счетные множества. Теорема о счетности произведения счетных множеств. Доказательство счетности множества рациональных чисел.

23. Мощность континуума. Теорема Кантора о несчетности множества точек на отрезке [0;1].

Источник