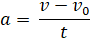Что такое объем в физике

Значение слова «объём»

1. Величина чего-л. в длину, высоту и ширину, измеряемая в кубических единицах. Объем геометрического тела. Объем куба. Объем здания.

2. Содержание чего-л. с точки зрения величины, размеров, количества и т. п. Объем работ. Объем розничной торговли. Объем знаний. Объем информации. □ Литературное наследство Гаршина очень невелико по объему. Короленко, В. М. Гаршин.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Единица измерения объёма в СИ — кубический метр; от неё образуются производные единицы, такие как кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель.

В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

ОБЪЁМ, а, м. 1. Величина в длину, ширину и высоту какого-н. тела с замкнутыми поверхностями, измеряемая в кубических единицах. О. шара. О. комнаты равен 140 куб. метрам. О. воды увеличивается при нагревании. 2. Величина, размеры. Книга небольшого объема. О. капитальных вложений в промышленность. || Содержание чего-н. с точки зрения величины, размеров, количества содержащегося. О. работ. О. знаний. Поставить проблему во всем объеме. ◊

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

объём

1. мера занимаемого телом пространства, измеряемая в кубических единицах

3. трёхмерное тело ◆ Несколько объёмов пересекаются, образуя многогранник.

4. внутренняя часть тела ◆ Предполагается, что электронейтральность образца устанавливается за счет движения электронов с поверхности в объём по дислокациям. В. Д. Куликов, «Ток проводимости в структуре металл — диэлектрик — металл», 2004.10.15 г. // «Журнал технической физики» (цитата из НКРЯ)

5. разг. техн. то же, что рабочий объём поршневого двигателя внутреннего сгорания ◆ Бензиновый двигатель объёмом 1,4 л обеспечивает максимальную скорость 90 км/ч и запас хода 400 км. Владимир Мосалев, «Легкие боевые машины иностранных государств», 2004.08.04 г. // «Солдат удачи» (цитата из НКРЯ)

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: цианид — это что-то нейтральное, положительное или отрицательное?

Источник

Объём

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Синонимом вместимости частично является ёмкость, но словом ёмкость обозначают также сосуды и качественную характеристику конденсаторов.

Принятые единицы измерения — в СИ и производных от неё — кубический метр, кубический сантиметр, литр (кубический дециметр) и т. д. Внесистемные — галлон, баррель.

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

Содержание

Вычисление объёма

Математически

В общем случае математически объём тела вычисляется по следующей интегральной формуле:

,

где — характеристическая функция геометрического образа тела.

Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен .

Через плотность

Объём находится по формуле:

Единицы объёма жидкости

Английские внесистемные

Американские внесистемные

Античные внесистемные

Древнееврейские

Русские внесистемные

Единицы сыпучих веществ

Английские внесистемные

Русские внесистемные

Молярный объём

Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:

Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль

Прочие единицы измерения

Примечания

Литература

Полезное

Смотреть что такое «Объём» в других словарях:

объём — объём, а … Русский орфографический словарь

объём — объём … Словарь употребления буквы Ё

объём — объём/ … Морфемно-орфографический словарь

объём — сущ., м., употр. сравн. часто Морфология: (нет) чего? объёма, чему? объёму, (вижу) что? объём, чем? объёмом, о чём? об объёме; мн. что? объёмы, (нет) чего? объёмов, чему? объёмам, (вижу) что? объёмы, чем? объёмами, о чём? об объёмах 1. В… … Толковый словарь Дмитриева

объём — а; м. 1. Величина чего л. в длину, высоту и ширину, измеряемая в кубических единицах. О. геометрического тела. О. куба, цилиндра. О. здания. О. полтора кубометра. В объёме (в трёх измерениях; объёмно). 2. Содержание чего л. с точки зрения… … Энциклопедический словарь

объём — объём, объёмы, объёма, объёмов, объёму, объёмам, объём, объёмы, объёмом, объёмами, объёме, объёмах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

ОБЪЁМ — ОБЪЁМ, а, муж. 1. Величина чего н. в длину, высоту и ширину, измеряемая в кубических единицах. О. пирамиды. О. здания. 2. Вообще величина, количество. Большой о. работ. О. информации. О. знаний. | прил. объёмный, ая, ое (к 1 знач.). Объёмное… … Толковый словарь Ожегова

объём — ОБЪЁМ1, а, м Величина или вместимость предмета, определяемая произведением длины, высоты и ширины и измеряемая в кубических единицах. Объем бассейна в новой школе составляет 300 кубических метров. ОБЪЁМ2, а, м Количество или величина чего л.… … Толковый словарь русских существительных

ОБЪЁМ — ОБЪЁМ, мера части пространства, занимаемого телом. Единицей измерения служит объём единичного куба … Современная энциклопедия

объ — объ. Пишется вм. (об) перед е, ю, я, напр. объехать, объявить.Примечание. Вм. этой приставки и следующей за ней буквы и пишется обы, напр. обыграть. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

объ… — Пишется вместо об… перед е, ю, я, напр. объехать, объявить. Примечание. вместо этой приставки и следующей за ней буквы и пишется обы, напр. обыграть. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

Источник

Определение площади и объема в физике с примером

Содержание:

Определение площади и объема:

В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.

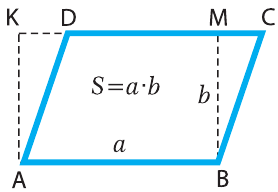
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.

Рис. 6.1.

Рис. 6.2.

Рис. 6.3

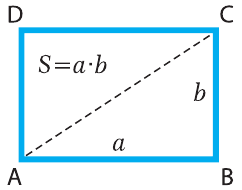
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.

Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
, (6.3)

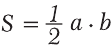
Значение числа 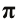можно получить, если разделить длину круга L на его диаметр. Причем не имеет значения, каков размер круга и в каких единицах измерены длина и диаметр (нужно только, чтобы это были одни и те же единицы).

Вычисление объема простых фигур

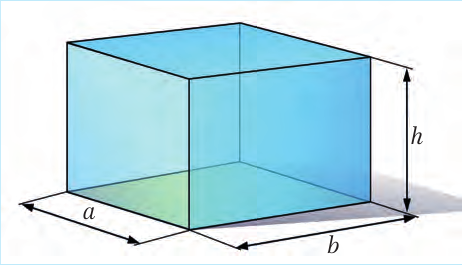
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):

Рис. 6.4.

Рис. 6.5.

Рис. 6.6.

V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:

V = S · h (6.5)
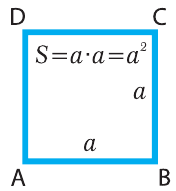
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a 3 (6.6)

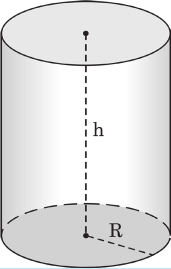
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR 2 · h (6.7)

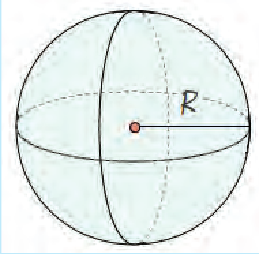
Объем шара (рис. 6.6)
(6.8)

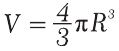
Единицы измерения объема

Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.

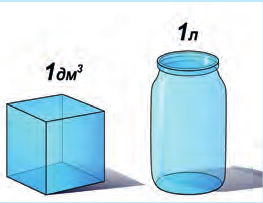
Рис. 6.7. Один литр – это 1дм 3

Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра

Таблица 6.1

Измерение объема тел неправильной формы

Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.

Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см 3 )

История:

Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!».

Итоги:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Изучаем объем, работу и другие явления: формулы физика 7 класс

Здравствуйте, дорогие друзья! Сегодня мы рассмотрим основные понятия физики и формулы, которые входят в программу учебника Физика 7 класс. Мы пройдем вкратце весь путь познания в области физики от таких базовых понятий, как объем и масса, до коэффициента полезного действия….

Количественные характеристики тела

Основные понятия физики – суть всех понятий, которые прямо или косвенно описывают природу явлений. Из количественных характеристик тела можно отметить его объем и массу. Приведем определение.

Объем представляет собой показатель того, сколько место занимает тело в пространстве. Уточним, что, если, к примеру, полая сфера и шар одинакового радиуса находятся в пространстве, то это не означает, что обе фигуры занимают в пространстве одинаковое количество места. Поясним это подробнее.

Полая сфера только на первый взгляд занимает столько же места, сколько шар, на деле их объемы различны – внутри сферы пустота, поэтому, рассчитывая объем, необходимо понимать, что объем воздуха внутри не входит в общую формулу.

Важно! Объем – величина, которая характеризует исключительно место, занимаемое телом. Объем не отражает суть влияние тела на само пространство и на другие тела. Тела одинаковой формы и размеров из совершенно различных материалов будут иметь одинаковые объемы. Формула объема также будет одинакова, как и его численное значение.

Для того чтобы характеризовать понятие объема, вспомним о том, каким образом мы измеряли размеры фигур на плоскости. Для этого мы пользовались понятием площадь. У плоских фигур не может быть объема, у объемных фигур может быть площадь, она называется площадью поверхности. Роль объема в физике очень велика, так как она отражает суть его размеров.

Приведем формулы некоторых фигур:

Формула объема параллелепипеда:

,

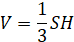
где S – основание, Н – высота.

,

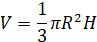
где R – радиус основания, Н – высота.

?=? ,

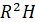
где R – радиус основания, Н – высота.

Говоря о массе, необходимо помнить, что эта физическая величина, в отличие от объема, как раз отражает влияние тела на окружающие тела. Масса представляет собой меру инерции тела, это физическая величина, которая определяет его гравитационные характеристики.

Не следует путать вес с массой, поскольку вес – это сила, и она зависит от гравитационных условий, в котором тело взвешивается.

Путь, время, скорость, ускорение

При движении тела оно проходит множество точек. Совокупность этих точек называется траекторией. Вектор между началом движения и концом называется перемещением. Если тело движется равномерно и прямолинейно, то перемещение, путь и расстояния равны.

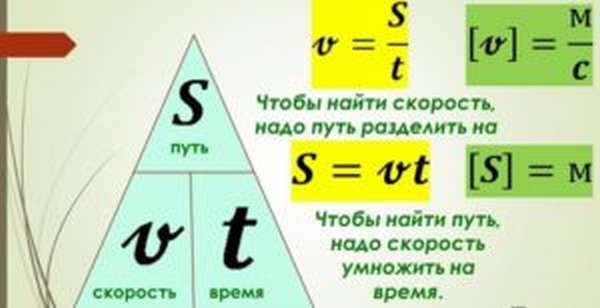
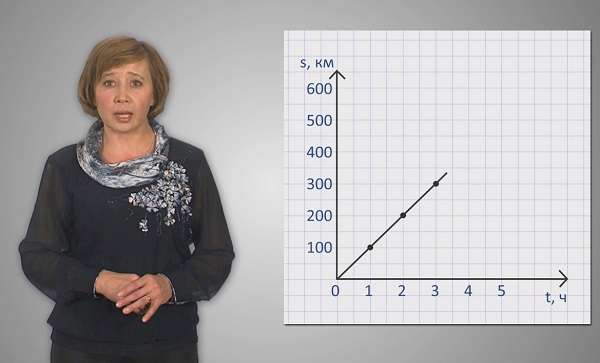
При движении с постоянной скоростью тело проходит за равные промежутки времени равные отрезки пути. Его путь можно отметить формулой:

v – скорость тела, t – время его пути. Понятие скорости в физике является одним из самых базовых, поскольку отражает общую тенденцию движущегося тела.

Если в течение времени t1 тело прошло расстояние S1, затем, изменив свою скорость, прошло расстояние S2 за время t2, то есть смысл говорить о таком понятии, как средняя скорость.

Явление средней скорости в общем понимании можно рассматривать как среднее арифметическое двух его скоростей:

.

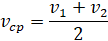
Если тело обе части пути проходило одно и то же расстояние S, то формула времени принимает вид:

.

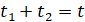
Запишем время как отношение расстояния к скорости:

.

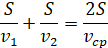
Тогда из этого соотношения можно получить выражение для средней скорости:

.

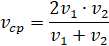
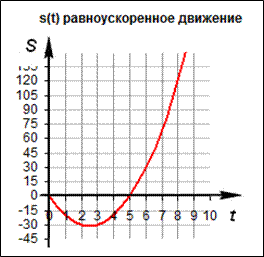
Если тело движется не с постоянной скоростью, но в течение одинаковых промежутков времени, его скорость одинаково меняется, то есть смысл говорить о равноускоренном движении (либо равнозамедленном, если скорость снижается, т.е. тело тормозит).

Важно! Именно равноускоренно двигаются все падающие тела. Ускорение соответствует ускорению свободного падения.

Введем понятие ускорения. Если тело двигалось со скоростью v0, спустя время t оно начало двигаться со скоростью v, то ускорением называется величина, равная:

В математике подобное отношение также называют производной скорости по времени. Зависимость скорости от каждого момента времени легко получить, отделив из формулы ускорения скорость:

.

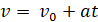
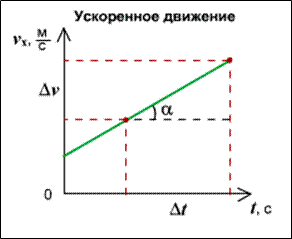
Изобразим график зависимости скорости от времени:

Очевидно, что графиком является прямая, причем тангенсом угла наклона этой прямой будет ускорение.

Площадь трапеции под графиком – расстояние, которое прошло тело. Вычислить эту площадь довольно просто, нам известно, что площадь трапеции является полусуммой ее оснований, умноженной на высоту. Одно основание трапеции равно v0 (как раз место, где прямая пересекает координату скорости), второе основание равно v. Высотой трапеции является ее сторона – время, т.е. t. Таким образом, площадь трапеции (пройденное расстояние) будет равна:

.

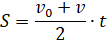
Поскольку v = v0 + at, получаем:

.

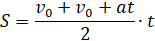
Таким образом, при равноускоренном движении расстояние равно:

.

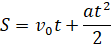
В случае, если речь идет о свободном падении, то вместо ускорения во все формулы должно быть поставлено ускорение свободного падения g=9,81 м/с2.

Если начальная скорость равна нулю, то:

.

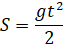
Графиком зависимости пути от времени будет парабола (поскольку зависимость квадратичная):

Постараемся найти формулу времени для разных типов движений:

При равномерном движении:

.

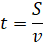
При равноускоренном движении:

.

Расчет скорости, пути и времени движения

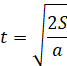
Вес, сила

Если кинематика занимается изучением того, как именно двигаются тела, то динамика подходит к понятию движения более глубоко – она изучают, почему они двигаются именно так. Здесь появляется понятие силы. Что такое сила в динамике? Данная физическая величина численно отражает уровень воздействия одного тела на другое. Измеряется она в ньютонах.

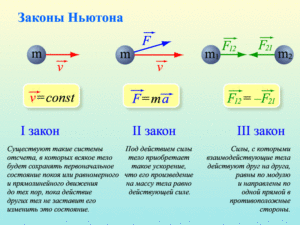
Больше всего физического смысла данной величины отражается в главных четырех законах, которые носят названия Три закона Ньютона и Закон всемирного тяготения.

Первый закон Ньютона гласит, что если сумма всех сил равна нулю, то тело движется равномерно. Не стоит путать сумма всех сил равна нулю и на тело не действуют никакие силы.

Знаменитый второй закон Ньютона устанавливает связь между динамической величиной силы, импульса и ускорения:

,

.

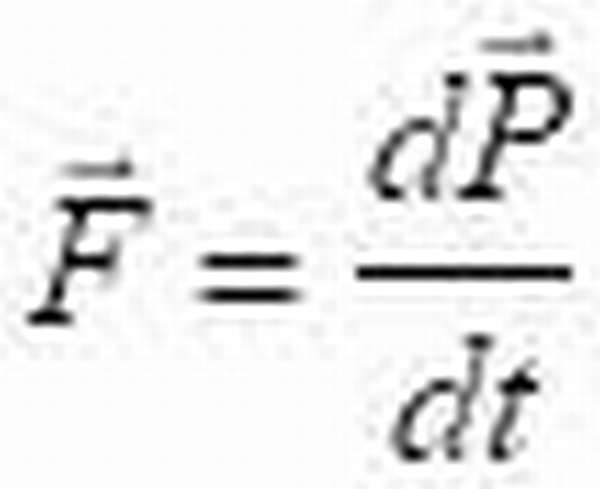
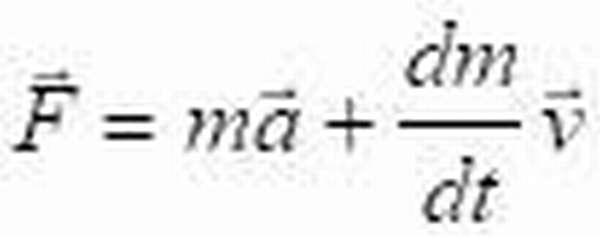
При постоянной массе:

В частности, если ускорение представляет собой ускорение свободного падения g, то сила превращается в вес:

Здесь мы на минуту остановимся и постараемся при помощи этих двух законов Ньютона усвоить несколько важных понятий.

Первый закон Ньютона гласит, что лежащее на поверхности тело хотя и находится в состоянии покоя (относительно земли), тем не менее, на него действуют две силы. Вес:

И нормаль (сила реакции опоры). Сумма этих сил равна нулю. Формула первого закона Ньютона может выглядеть таким образом:

Если .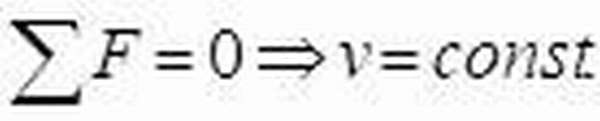

Вес является величиной относительной с точки зрения планет, на которых находятся тела. Например, часто можно услышать ошибочное высказывание: масса тела на Луне меньше, чем на Земле. Это не так. Массы на всех планетах одинаковые, а вот вес разный, поскольку различается ускорение свободного падения. Именно поэтому космонавты на Луне с такой легкостью подпрыгивали – их вес на Луне был значительно ниже, чем на Земле, ведь Луна их притягивала к себе не так сильно, как Земля.

Третий закон Ньютона гласит, что сила действия равна силе противодействия. Иными словами, чем сильнее мы давим на тело, тем сильнее оно давит на нас. Этот закон отражает равенство силы тяжести и нормали.

.

,

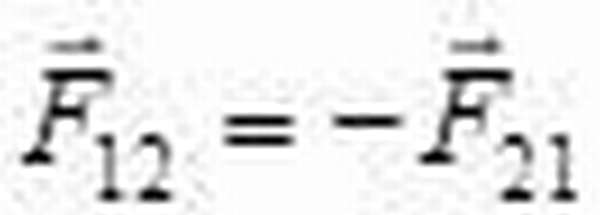
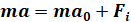
где Fi сила инерции.

Если есть система тел, то скорость центра масс системы равна:

.

Три закона Ньютона

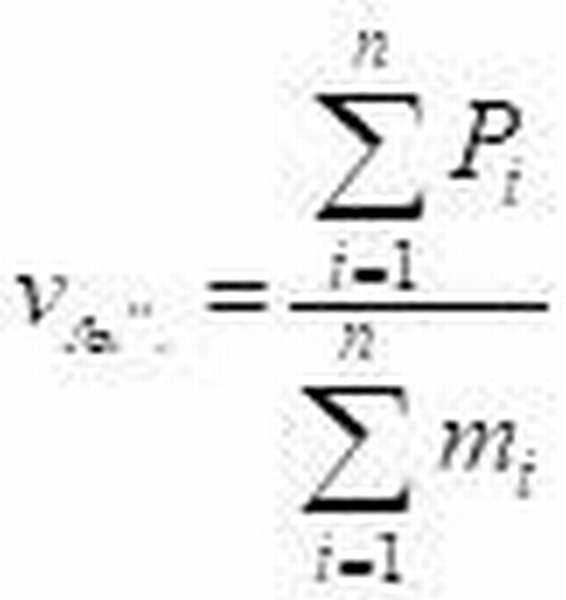
Закон всемирного тяготения, который еще называют четвертым законом Ньютона, гласит:

,

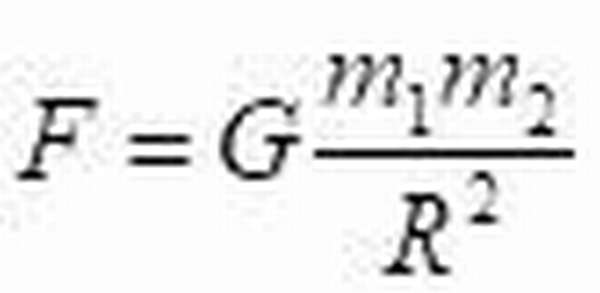
где G – гравитационная постоянная, m1, m2 – массы притягивающихся тел.

Если в левой части этого равенства указать вес, то получаем формулу для ускорения свободного падения тел на любой планете:

.

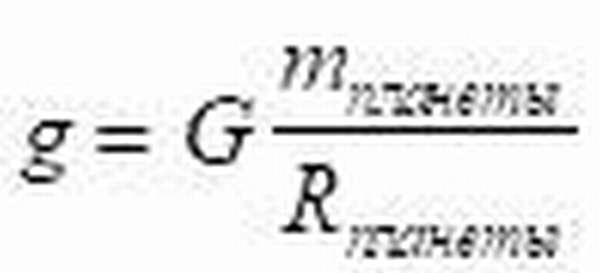
Также, из закона всемирного тяготения выводится понятие первой космической скорости, т.е. скорости, при которой тело покидает гравитационное поле. Именно до этой скорости (на Земле она равна 7,9 км/с) разгоняют ракеты, которые необходимо вывести на орбиту.

Первая космическая скорость:

.

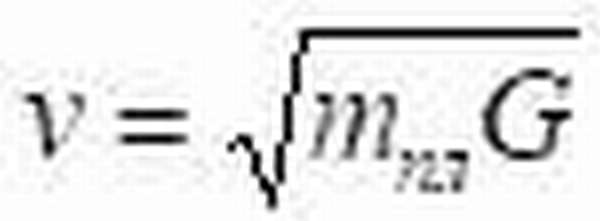
Вернемся к понятию веса.

Если тело находится в состоянии покоя, то вес равен:

Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:

Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:

Эта формула наглядно показывает, что в падающем лифте, где а = g, вес тела будет равен нулю, т.е. тело испытает невесомость.

Если тело движется по выпуклой траектории, то ускорение, действующее на него, – центробежное, а значит вес:

Если тело движется по вогнутой траектории, то ускорение действующее на него тоже центробежное и направлена от центра, а значит вес:

Формула силы трения:

,

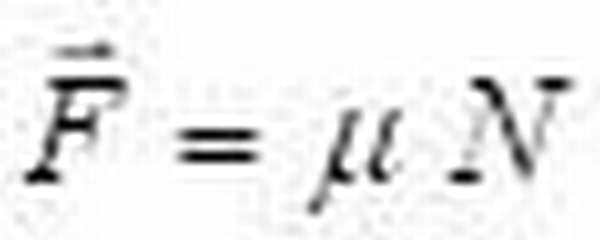
где 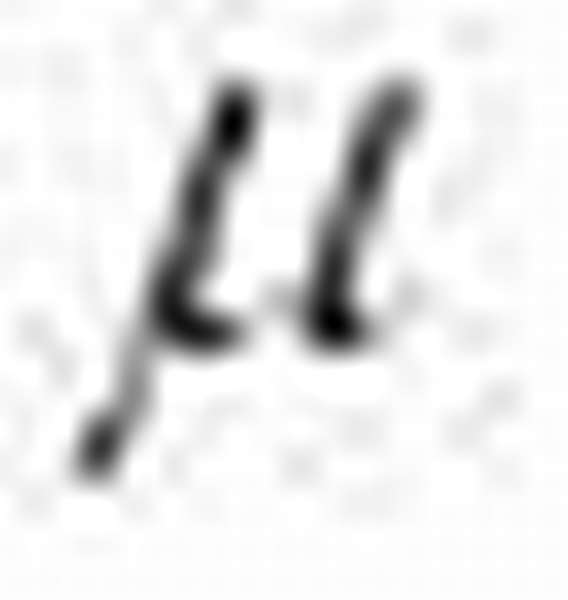коэффициент трения, N нормаль (реакция опоры).

Таким образом, мы познакомились уже с несколькими видами сил – вес (сила тяжести), сила трения, центробежная сила, сила всемирного тяготения (которая является по сути тем же весом, только в более общей форме).

Рассмотрим еще одну силу, которая имеет место в случае деформаций. Она называется силой упругости. Закон Гука для малых деформаций (сжатий или растяжений) гласит, что сила, действующая на тело, длину которого деформировали на х, равна:

Из этого закона вытекает ряд следствий, например модуль Юнга, который выступает коэффициентом пропорциональности в связи между нормальным напряжением и относительным изменением длины:

.

Центробежная сила

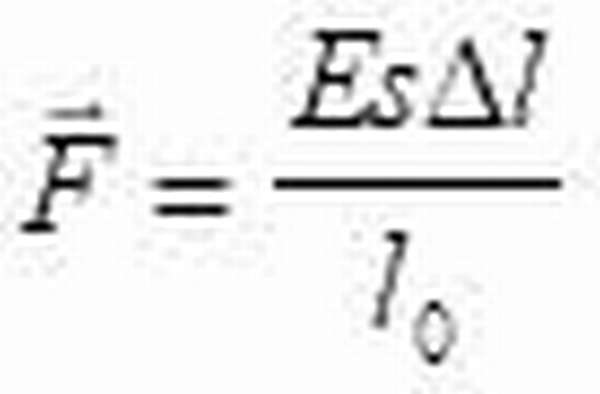
Энергия, работа, мощность, полезное действие

Для того чтобы описывать различные формы взаимодействия материи и ее движение, вводится физическая величина энергия. Если тело прошло расстояние S из-за того, что на него в это время действовала сила F, то энергия этого движения называет работой этого тела. Формула работы записывается таким образом (произведение силы и пройденного пути):

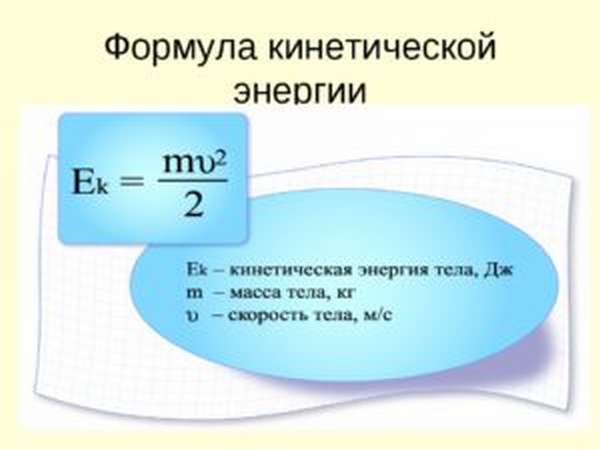
Если тело движется со скоростью v, то тело обладает энергией, которая называется кинетической:

.

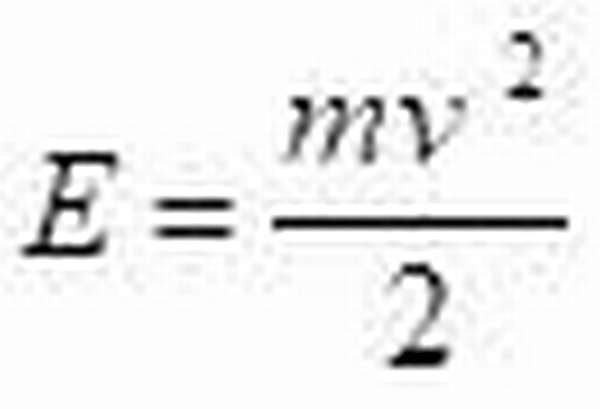
Если тело приподняли на высоту h, то оно обладает в точке подъеме потенциальной энергией:

При падении тела с высоты Н его потенциальная энергия превращается в кинетическую.

Закон сохранения энергии гласит, что в замкнутых системах энергия сохраняется. Таким образом, если тело подняли на высоту h и отпустили, то скорость, с которой оно будет приземляться, можно вычислить из закона сохранения:

.

.

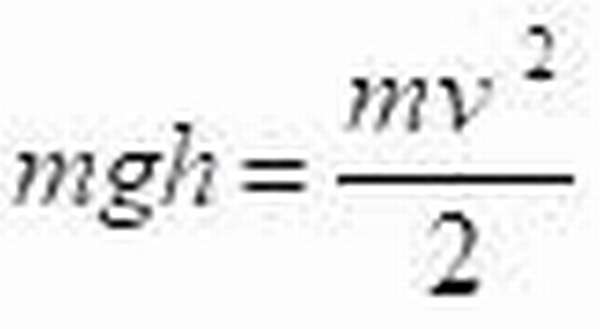
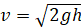
Остановимся подробнее на двух законах сохранения: законе сохранения энергии и импульса.

Импульс в замкнутых системах сохраняется, энергия в замкнутых системах сохраняется. В паре эти два закона могут разрешить бесконечное количество задач. Рассмотрим пример.

Кинетическая энергия

Задача на закон сохранения энергии и импульса

Какая будет скорость u шарика массой M и скорость v1 шарика массой m после удара?

Первый шарик до столкновения обладал импульсом mv. Второй шарик находился в состоянии покоя, т.е. его импульс был равен M∙0 = 0.

Таким образом, в системе двух шариков суммарный импульс до столкновения был равен:

.

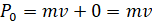
После столкновения импульс первого шарика стал равен mv1, а импульс второго шарика составил Mu. Тогда суммарный импульс системы двух шариков после удара равен:

Согласно закону сохранения импульса Р = Р1, а именно:

(1).

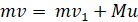
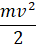
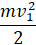
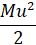
Теперь рассмотрим энергии. Кинетическая энергия первого шарика до удара составила . Кинетическая энергия второго шарика равна нулю. После удара первый шарик имеет кинетическую энергию . Второй шарик после удара обладает энергией: .

Согласно закону сохранения энергии:

.

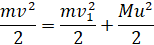
Сократив двойки в знаменателях, получаем:

(2).

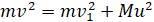
Получаем систему из двух выражений (1) и (2).

(*).

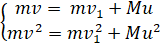
Из первого уравнения можем получить выражение для скорости первого шарика после удара:

(3).

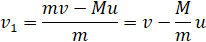
Найдем квадрат этой скорости:

.

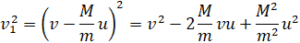
Найдем значение выражения:

.

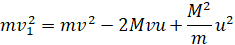
Теперь можно подставить это выражение во второе уравнение системы (*):

.

.

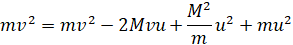
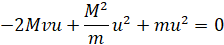
Выводим квадрат скорости u за скобки:

.

.

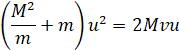
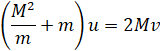
Таким образом, скорость второго шарика после удара составляет:

.

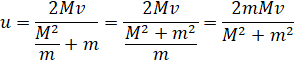
Подставив это в выражение (3), можем найти скорость первого шарика после удара:

.

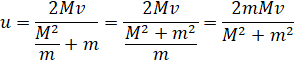
Это был один из немногих примеров того, каким образом при помощи двух законов сохранения находить величины.

Траты энергии. КПД

Однако, говоря об энергии, следует помнить о ее тратах. Например, если во время работы какой-либо физической системы (движущееся тело или тепловая машина) затраченная энергия Q привела к тому, что система произвела полезную энергию A, то говорят о так называемом коэффициенте полезного действия (КПД). КПД измеряется в процентах, которые численно отображают отношение полезной энергии (которую дает система) ко всей суммарно использованной.

Формулу КПД записывают в таком виде:

,

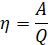
либо, если в процентах:

.

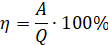
КПД всегда меньше единицы, поскольку полезная работа не может быть больше суммарной, а закон сохранения энергии должен соблюдаться.

Не существует КПД 100%, поскольку траты (даже самые малые) есть в любых системах.

Источник