Что такое нормальный вектор

Нормальный вектор прямой

Вы будете перенаправлены на Автор24

В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.

Нормаль – синоним для слова перпендикуляр.

Можно выразить уравнение прямой и другим способом:

Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ

Нормальное уравнение прямой можно выразить и в тригонометрическом виде:

$x \cdot \cos <\alpha>+ y \cdot \sin <\alpha>— p = 0$

Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:

Готовые работы на аналогичную тему

Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.

Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:

Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.

Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.

то нормальный вектор описывается формулой:

При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.

В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:

Подставив значения, получаем:

Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:

Что соответствует числам исходных данных.

Равенство верно. Осталось лишь найти формулу направляющего вектора:

$\bar

(-B; A) \implies \bar

(1; 3)$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 03 2021

Источник

Нормальный вектор прямой, координаты нормального вектора прямой.

При изучении уравнений прямой линии на плоскости и в трехмерном пространстве мы опираемся на алгебру векторов. При этом особое значение имеют направляющий вектор прямой и нормальный вектор прямой. В этой статье мы подробно рассмотрим нормальный вектор прямой. Начнем с определения нормального вектора прямой, приведем примеры и графические иллюстрации. Следом перейдем к нахождению координат нормального вектора прямой по известным уравнениям прямой, при этом покажем подробные решения задач.

Навигация по странице.

Нормальный вектор прямой – определение, примеры, иллюстрации.

Для понимания материала Вам необходимо иметь четкое представление о прямой линии, о плоскости, а также знать основные определения, связанные с векторами. Поэтому рекомендуем сначала освежить в памяти материал статей прямая на плоскости, прямая в пространстве, представление о плоскости и векторы – основные определения.

Дадим определение нормального вектора прямой.

Из определения нормального вектора прямой понятно, что существует бесконечное множество нормальных векторов данной прямой.

Определение нормального вектора прямой и определение направляющего вектора прямой позволяют заключить, что любой нормальный вектор данной прямой перпендикулярен любому направляющему вектору этой прямой.

Приведем пример нормального вектора прямой.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям этой прямой.

Найдем ответ на поставленный вопрос для прямых, заданных на плоскости уравнениями различного вида.

Если прямую линию на плоскости определяет общее уравнение прямой вида , то коэффициенты А и B представляют собой соответствующие координаты нормального вектора этой прямой.

Найдите координаты какого-нибудь нормального вектора прямой .

Одно из чисел A или B в общем уравнении прямой может равняться нулю. Это не должно Вас смущать. Рассмотрим на примере.

Укажите любой нормальный вектор прямой .

Нам дано неполное общее уравнение прямой. Его можно переписать в виде , откуда сразу видны координаты нормального вектора этой прямой: .

Уравнение прямой в отрезках вида или уравнение прямой с угловым коэффициентом легко приводятся к общему уравнению прямой, откуда и находятся координаты нормального вектора этой прямой.

Найдите координаты нормального вектора прямой .

От уравнения прямой в отрезках очень легко перейти к общему уравнению прямой: . Следовательно, нормальный вектор этой прямой имеет координаты .

Также можно получить координаты нормального вектора прямой, если привести каноническое уравнение прямой или параметрические уравнения прямой к общему уравнению. Для этого производят следующие преобразования:

Как способ предпочесть – решать Вам.

Покажем решения примеров.

Найдите какой-нибудь нормальный вектор прямой .

Второй способ решения.

Перейдем от канонического уравнения прямой к общему уравнению: . Теперь стали видны координаты нормального вектора этой прямой .

или

Укажите координаты какого-либо нормального вектора прямой, заданной параметрическими уравнениями .

Перейдем к общему уравнению этой прямой. Для этого выполним следующие действия:

Теперь видны координаты нормального вектора прямой: .

Если прямая задана уравнениями двух пересекающихся плоскостей и , то ее нормальным вектором является как нормальный вектор плоскости , так и нормальный вектор плоскости , то есть, векторы и .

Источник

Нормальный вектор плоскости, координаты нормального вектора плоскости.

Хорошее представление о прямой линии начинается с момента, когда вместе с ее образом одновременно возникают образы ее направляющих и нормальных векторов. Аналогично, при упоминании о плоскости в пространстве, она должна представляться вместе со своим нормальным вектором. Почему так? Да потому что во многих случаях удобнее использовать нормальный вектор плоскости, чем саму плоскость.

В этой статье мы сначала дадим определение нормального вектора плоскости, приведем примеры нормальных векторов и необходимые графические иллюстрации. Далее поместим плоскость в прямоугольную систему координат в трехмерном пространстве и научимся определять координаты нормального вектора плоскости по ее уравнению.

Навигация по странице.

Нормальный вектор плоскости – определение, примеры, иллюстрации.

Для хорошего усвоения материала нам потребуется хорошее представление о прямой в пространстве, представление о плоскости и определения из статьи векторы – основные определения.

Дадим определение нормального вектора плоскости.

Из определения следует, что существует бесконечное множество нормальных векторов данной плоскости.

Так как все нормальные векторы заданной плоскости лежат на параллельных прямых, то все нормальные векторы плоскости коллинеарны. Другими словами, если — нормальный вектор плоскости , то вектор при некотором ненулевом действительном значении t также является нормальным вектором плоскости (смотрите статью условие коллинеарности векторов).

Также следует заметить, что любой нормальный вектор плоскости можно рассматривать как направляющий вектор прямой, перпендикулярной к этой плоскости.

Множества нормальных векторов параллельных плоскостей совпадают, так как прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и ко второй плоскости.

Из определения перпендикулярных плоскостей и определения нормального вектора плоскости следует, что нормальные векторы перпендикулярных плоскостей перпендикулярны.

Приведем пример нормального вектора плоскости.

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.

Общее уравнение плоскости вида определяет в прямоугольной системе координат Oxyz плоскость, нормальным вектором которой является вектор . Таким образом, чтобы найти координаты нормального вектора плоскости нам достаточно иметь перед глазами общее уравнение этой плоскости.

Рассмотрим несколько примеров.

Найдите координаты какого-либо нормального вектора плоскости .

Плоскость задана уравнением . Определите координаты ее направляющих векторов.

Нам дано неполное уравнение плоскости. Чтобы стали видны координаты ее направляющего вектора, перепишем уравнение в виде . Таким образом, нормальный вектор этой плоскости имеет координаты , а множество всех нормальных векторов запишется как .

Уравнение плоскости в отрезках вида , как и общее уравнение плоскости, позволяет сразу записать один из нормальных векторов этой плоскости – он имеет координаты .

В заключении скажем, что с помощью нормального вектора плоскости могут быть решены различные задачи. Самыми распространенными являются задачи на доказательство параллельности или перпендикулярности плоскостей, задачи на составление уравнения плоскости, а также задачи на нахождение угла между плоскостями и на нахождение угла между прямой и плоскостью.

Источник

Нормальный вектор плоскости

Вы будете перенаправлены на Автор24

Для каждой плоскости существует бесконечное множество коллинеарных друг по отношению к другу нормальных векторов.

Рисунок 1. Векторы в трехмерной системе координат. Автор24 — интернет-биржа студенческих работ

Рассмотрим основные математические закономерности, показываюшие как найти вектор нормали к плоскости.

$Ax + D = 0 \\ By + D = 0 \\ Cz + D = 0$

Готовые работы на аналогичную тему

$\overline \cdot N = 0$

Переписав уравнение через проекции, получим

Это дает нам возможность выводить уравнение плоскости через координаты точки и параметры нормального вектора плоскости.

Определить плоскость в пространстве можно и другими способами, например, с помощью указания координат трех ее точек, не лежащих на одной прямой, двух неколлинеарных векторов и точки и т.д. Однако форма записи с помощью нормального вектора плоскости и точки наиболее компактна. К ней другие методы задания плоскости можно привести путем алгебраических преобразований.

С помощью нормального вектора плоскости как ее определителя могут быть решены задачи на доказательство параллельности или перпендикулярности плоскостей, на составление уравнения плоскости, на нахождение угла между прямой и плоскостью, на нахождение угла между плоскостями.

Для начала найдем коэффициенты, соответствующие координатам:

Подставим значения в формулу:

После стандартных преобразований получим ответ:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 03 2021

Источник

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

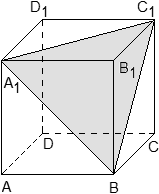
· Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Решение. Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − B = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Ответ: n = (− 1; 1; − 1)

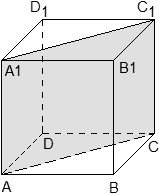
· Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Решение. В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Ответ: n = (− 1; 1; 0)

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Источник