Что такое нормальное гравитационное поле
Нормальное гравитационное поле и его аномалии.
Нормальное гравитационное поле – это такое поле, которое имела бы Земля, если бы у нее была форма эллипсоида вращения с правильным распределением масс в нем. Нормальное поле изменяется строго по широте.
Существуют три основные поправки: поправка за свободный воздух, за промежуточный слой и за окружающий рельеф.
Поправка за свободный воздух учитывает разницу в уровне наблюдения и уровне сфероида и рассчитывается по формуле (в мГал)
где h– расстояние от точки наблюдения до уровня моря, м.
Поправку за промежуточный слой вводят для исключения влияния масс, расположенных между поверхностью наблюдений и сфероидом: Δgс=0,041ρh,
Поправка за окружающий рельеф вводится для более точного учета притяжения рельефа местности, окружающего пункт наблюдения. Определяется эта поправка по специальным таблицам в тех случаях, если отклонения рельефа местности в районе наблюдения значительны (горные районы, переходные и рифтовые зоны и др.).
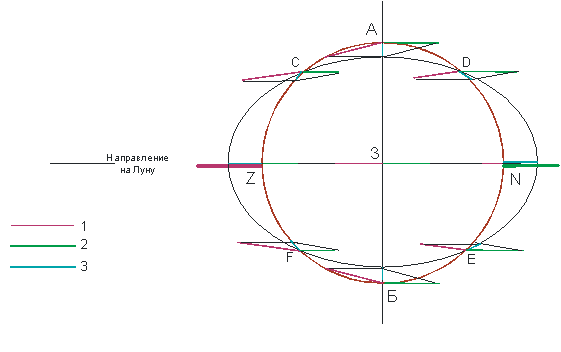
В точках Z и N приливообразующие силы, направленные вдоль радиуса Земли, уменьшают силу тяжести, а в точках А и В–увеличивают ее. В промежуточных точках С, D, F и Е приливообразующие силы направлены по касательной к земной поверхности.
Рис. 4.3 – Приливообразующие силы Луны: 1 – сила тяготения; 2 – центробежная; 3 – равнодействующая
Вследствие суточного вращения Земли приливные выступы (приливные волны) перемещаются по поверхности океанов с периодом, равным 24 ч («солнечные сутки») для солнечной приливной волны, и 24 ч 50 мин («лунные сутки») для лунной. За это время бывает два прилива (полная вода) и два отлива (малая вода).
Величина прилива во многом зависит от конфигурации берегов и рельефа дна. Приливы происходят в атмосфере, где они проявляются в периодических изменениях атмосферного давления, причем наиболее четко выражена волна с периодом 12 ч.
Геофизика
1.1. Основы теории гравиразведки
1.1.1. Нормальное гравитационное поле Земли
Согласно закону всемирного тяготения все тела притягиваются друг к другу с силой, пропорциональной их массе и обратно пропорциональной квадрату расстояния между ними. Для точечных масс, т. е. для масс, сосредоточенных в бесконечно малом объеме, справедлив закон всемирного тяготения Ньютона :
Если силу притяжения отнести к единичной массе ( т 1 = 1), то точечная масса ( т 2 = m ) будет притягивать ее с силой, равной ускорению силы притяжения :
В случае притяжения единичной массы телом, состоящим из отдельных точек ( n ) с массой ( m i ), ускорение силы притяжения принимает вид
При непрерывном распределении притягиваемых масс сумма заменяется интегралом по всему занимаемому массами объему ( V ):
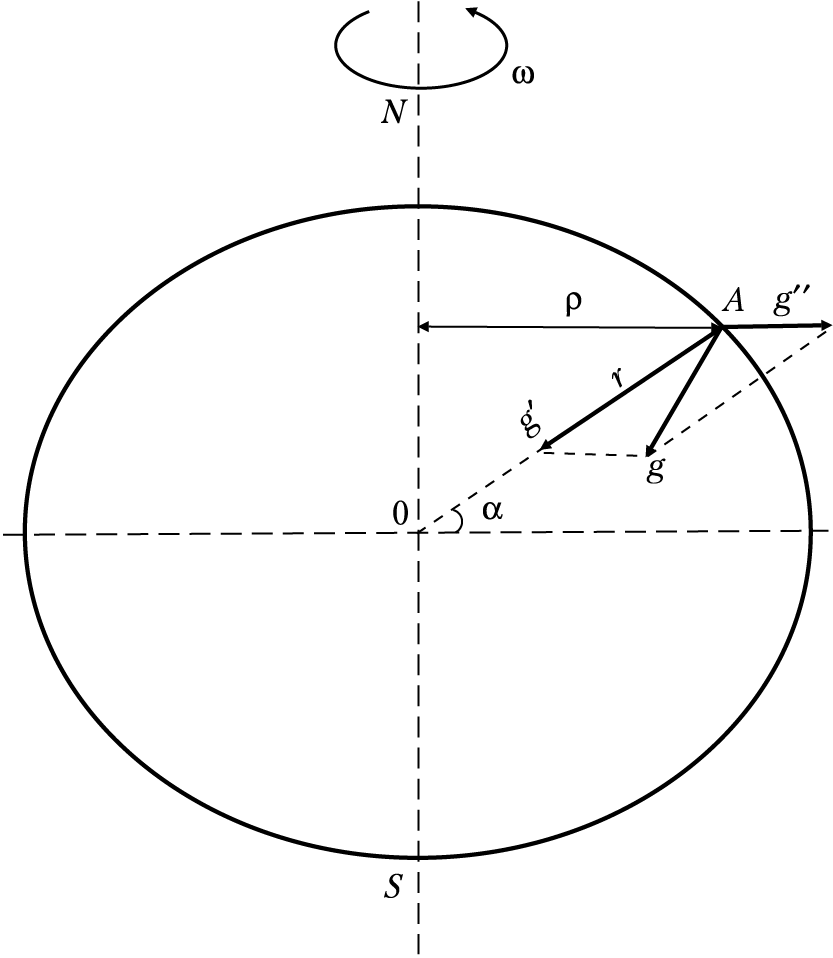
где М — масса Земли; r — средний радиус Земли, если притягиваемая точка А находится на ее поверхности (рис. 1.1).
Рис. 1.1. Нормальное поле силы тяжести и составляющие силы тяжести:
В общем случае нормальное гравитационное поле ( γ 0 ) Земли в виде шара представляет собой равнодействующую ускорений притяжения ( g ′ ) и центробежной силы ( g ′′ ):
Если представить форму Земли в виде эллипсоида вращения малого сжатия ( α = 298,26), нормальное значение ускорения силы тяжести ( γ 0 ) можно выразить, например, по Элкинсу, формулой
γ 0 = g норм = g э (1 + 0,005302sin 2 φ – 0,000007sin 2 2 φ ), (1.9)
где g э — среднее значение поля на экваторе Земли; φ — широта наблюдения.
Это выражение позволяет рассчитать γ 0 на поверхности геоида, т. е. уровенной поверхности однородной Земли, совпадающей с невозмущенной поверхностью океана. С ростом количества точек наблюдений и повышением точности самих измерений g численные коэффициенты и их количество в формуле (1.9) будут меняться, поэтому существует несколько вариантов аналитического расчета значений нормального гравитационного поля как для всей поверхности Земли, так и для территорий отдельных государств, что необходимо учитывать при анализе гравитационных данных сопряженных или пограничных территорий.
1.1.2. Аномалии и редукции силы тяжести
Аномалией силы тяжести называют отклонение наблюденного значения ( g набл ) от нормального поля, теоретически рассчитанного для этой же точки, например, по формуле
где h — высота точки наблюдения над уровнем моря, выраженная в метрах.
Аномалией Фая ( Δ g Ф ) называют аномалию силы тяжести, полученную с учетом различия высот точек наблюдения:
Поправку за свободный воздух вводят в g набл со знаком плюс, если наблюдения проводят над уровнем моря, и со знаком минус, если наблюдения осуществляются ниже уровня моря. При погрешности относительных гравиметрических измерений ±0,01 мГал разница в высотах должна быть известна с погрешностью не более 4 см.
Аномалии Фая в основном используют в геодезической гравиметрии, а также при оценке геодинамического состояния земной коры и литосферы.
При наземных съемках на участках, приподнятых по отношению к уровню геоида, между поверхностью наблюдения и геоидом располагаются массы горных пород, которые при введении поправки за свободный воздух виртуально смещаются на величину h и «накладываются» на нижележащие массы, создавая как бы двойной плотностной эффект. Для исключения влияния масс, расположенных между поверхностью наблюдения и уровнем нормального поля, вводят поправку за промежуточный слой — поправку Буге ( Δ g Б ). Для выровненного спокойного рельефа поверхности наблюдения, когда массы промежуточного слоя можно представить в виде плоскопараллельного горизонтального слоя мощностью h (в м), эту поправку вычисляют по формуле (в мГал)
При расположении точки наблюдения выше уровня моря поправку Δ g Б вводят в наблюденные значения силы тяжести со знаком минус.
Поправка Буге, или полная поправка за промежуточный слой, имеет вид
В зависимости от точности наблюдений используют топографические карты различного масштаба, с помощью которых определяют влияние масс рельефа в области радиусом порядка 200 км и более от точки наблюдения. Причем для близко расположенных к точке наблюдения участков необходимы более точные карты рельефа местности.
Аномалия Буге ( Δ gБ ) представляет собой разность наблюденного и теоретического полей силы тяжести при введении соответствующих поправок:
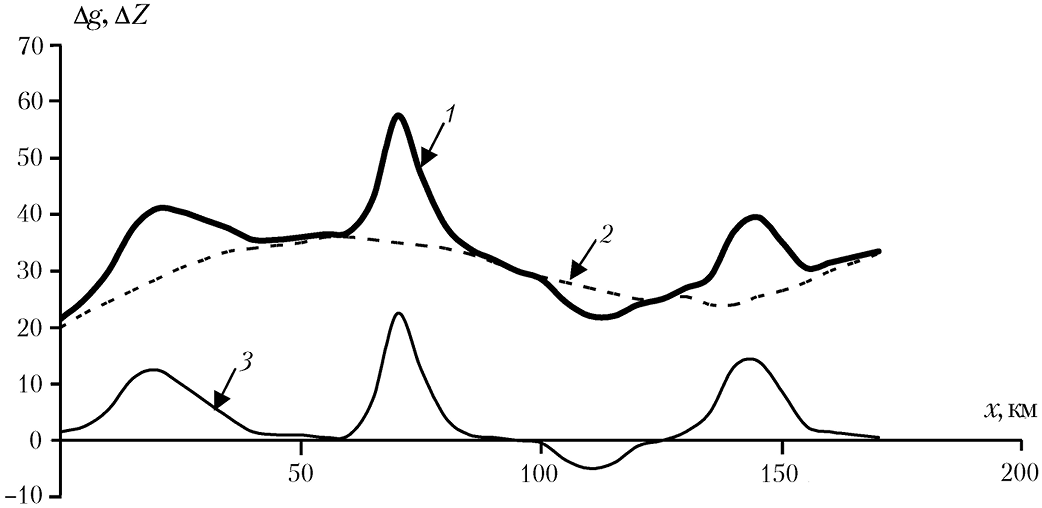
Аномалии Буге практически каждой территории представлены набором аномалий от разноглубинных и разномасштабных плотностных неоднородностей, отражающих локальные и региональные составляющие (рис. 1.2). Такое разделение аномалий связано с их разной частотной характеристикой: более высокочастотные аномалии относятся к локальным, а более низкочастотные — к региональным. Для выявления локальных аномалий Буге ( Δ g лок ) от, например, геологических структур осадочных бассейнов, отдельных интрузий, карстовых образований, рудных тел и других из наблюденного поля ( Δ g набл ) исключают региональную составляющую ( Δ g рег ), вычисляемую различными математическими (статистическими и др.) способами. На рисунке 1.2 приведен пример графического сглаживания наблюденного поля и выделения плавно изменяющегося регионального поля и локальной аномалии: Δ g лок = Δ g набл – Δ g рег (подробнее см. 1.4.2).
Рис. 1.2. Наблюденные (1), региональные (2) и локальные (3) аномалии силы тяжести
1.1.3. Плотность горных пород
Плотность горных пород и руд главным образом зависит от химико-минерального состава и пористости. Плотность изверженных и метаморфических пород определяется в основном минеральным составом и увеличивается при переходе от пород кислых к основным и ультраосновным в соответствии с увеличением железосодержащих минералов. Для осадочных пород плотность определяется прежде всего пористостью, водонасыщенностью и в меньшей степени минералогическим составом. Некоторые значения плотности приведены в табл. 1.1.
Таблица 1.1. Плотность некоторых веществ, пород, минералов и оболочек Земли
Нормальное и аномальное гравитационное поле
Как и во всех геофизических полях, в гравитационном поле Земли можно выделить нормальное и аномальное поле.
Нормальным полем считается теоретически рассчитанное поле для поверхности эллипсоида вращения или сфероида, которым в первом приближении является Земля. Величина сжатия земного эллипсоида равна:
Задача о распределении силы тяжести на поверхности сфероида была решена французским математиком Клеро в 1743 году. Исходя из допущения, что Земля состоит из однородных жидких слоев, плотность которых увеличивается к ее центру, он вывел формулу для вычисления величины нормальной силы тяжести go в зависимости от географической широты φ пункта Земли. В упрощенном виде она выглядит следующим образом:
Путем многочисленных измерений силы тяжести на поверхности Земли и на основе теоретических разработок о распределении плотности внутри нее, были получены значения числового коэффициента для этой формулы. Практически, из-за того, что разные авторы использовали различные исходные данные и предпосылки, существует несколько формул определения go.
В действительности Земля имеет более сложную форму и более сложное внутреннее строение. Поэтому наблюдаемое на реальной поверхности гравитационное поле будет отличаться от нормального поля. Как известно, разность между наблюденным полем и нормальным составляет аномальную часть. В общем виде аномальное поле можно представить как:
Поправка за высоту вводится для приведения силы тяжести к уровню моря. Для ее вычисления полагают, что между точкой наблюдения А (рис. 4.2), расположенной на некоторой высоте h, и уровнем моря нет притягивающих масс.
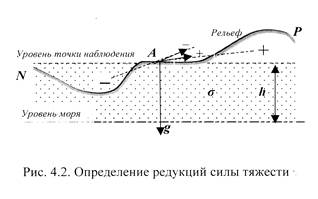
Поправка за промежуточный слой учитывает влияние масс, расположенных между точкой наблюдения А и уровнем моря (см. рис 4.2). Формула для вычисления этой поправки выведена в предположении, что Земля имеет ровный рельеф, и слой между поверхностью наблюдения и уровнем моря можно представить в виде плоско-параллельного безграничного слоя, однородного по составу.
Поправка имеет отрицательный знак, потому что притяжение промежуточного слоя, находящегося под пунктом наблюдений, увеличивает силу тяжести.
Поправка за влияние окружающего рельефа местности (или топографическая поправка) вводится в связис тем, что при определении поправки за промежуточный слой поверхность Земли предполагалась ровной. В реальности влияние рельефа может достигать нескольких десятков миллиГал.
Избыток или недостаток масс, связанный с формами рельефа, всегда уменьшает наблюденное значение силы тяжести. Поэтому эта поправка всегда имеет положительный знак.
В самом деле, избыток масс над уровенной поверхностью, проходящей через точку наблюдения А, под отрезком АР рельефа Земли (см. рис. 4.2) создает добавочную силу (+), направленную в сторону центра избытка масс (+), и вертикальная составляющая этой силы направлена вверх, то есть уменьшает значение g. Недостаток масс под уровенной поверхностью над отрезком рельефа АN создает добавочную силу (-), направленную в сторону центра недостатка масс (-), вертикальная составляющая которой направлена вверх и тоже уменьшает величину g относительно той величины, которая должна была быть при однородном распределении масс под уровенной поверхностью.
Введение всех указанных поправок позволяет привести аномальное поле силы тяжести к некоторой поверхности, которую назвали геоидом (что означает «землеобразный»). Под геоидом подразумевают поверхность, совпадающую на океанах с уровнем воды и мысленно продолженную под континенты.
Теперь, мы имеем возможность дать более точное определение аномалии силы тяжести.
Аномалией силы тяжести называется разность между наблюденным значением силы тяжести на дневной поверхности с поправками и нормальным значением, вычисленным по соответствующей формуле.
Таким образом, выражение для аномалии силы тяжести может быть записано:
∆g =gн– g0+ ∆´g
Гравитационное поле
Под гравитационным полем Земли понимается поле силы тяжести (ускорения силы тяжести), которая определяется как составляющая двух основных сил: силы притяжения Земли и центробежной силы, вызванной её суточным вращением. Влияние других факторов (притяжения Луны, Солнца и других небесных тел и масс атмосферы) на значение силы тяжести учитывается соответствующими поправками.
Изменение силы тяжести на 1мГал соответствует:
· перемещению над поверхностью Земли на 3м;
· притяжению слоя грунта толщиной 10м (при плотности земной коры 2,67г/см 3 );
· перемещению на 1,23 км по широте на параллели 45°.
Гравитационное поле Земли принято разделять на две части: нормальное гравитационное поле и остаточное аномальное поле. Основное преимущество такого разделения состоит в том, что аномальное поле гораздо слабее действительного гравитационного поля Земли и поэтому его характеристики легче определить. Термин «аномалии» означает отклонение от некоторой «нормы», т.е. значение, которые можно предсказать, вычислив его по формуле
Нормальное гравитационное поле (гравитационное поле Нормальной Земли) характеризуется четырьмя параметрами: общей массой Земли, формой и размерами эллипсоида, наиболее близко соответствующего геоиду в глобальном масштабе, скоростью вращения Земли. Его определение вытекает из условия, что поверхность эллипсоида есть уровенная поверхность в нормальном гравитационном поле, а поверхность геоида представляет собой уровенную поверхность в действительном гравитационном поле. При этом предполагается, что центр нормального эллипсоида (или референц-эллипсоида) совпадает с центром масс Земли.

Рис.1.38. Общий вид гравиметра ГНК-К2
Геодезическая практика в значительной мере сосредоточена на измерении силы тяжести. Наиболее распространённым прибором для измерения силы тяжести является гравиметр, используемый для измерений разности силы тяжести между двумя пунктами (относительные измерения). Этот прибор (рис.1.38) работает на принципе компенсации изменений притяжения массы маятника гравиметра упругими силами закрученной кварцевой нити, на которой подвешен маятник. Достоинствами таких гравиметров являются малые размеры и высокая точность измерений (до 0,01 миллигал).
Для получения действительного значения силы тяжести в любом пункте относительные измерения в заданном пункте связывают с данными абсолютных измерений силы тяжести в этом пункте с помощью баллистического гравиметра. Точность измерения баллистическим гравиметром достигает 0,01 миллигал. Большинство баллистических гравиметров размещается в стационарных лабораториях, однако существуют и транспортабельные устройства, имеющие приемлемые точности измерения.
В совершенствовании измерений параметров гравитационного поля Земли важная роль принадлежит спутниковой альтиметрии, использующей радиолокационные альтиметры, размещаемые на борту орбитальных спутников.
Идея спутниковой альтиметрии достаточно проста (рис.1.39): расстояние от спутника Q (r, φ – геоцентрические радиус и широта спутникового радиовысотомера) до поверхности океана (точка Q¢) определяется с помощью электронных устройств, измеряющих время, за которое радиоволны проходят это расстояние и обратный путь до бортового приёмного устройства после отражения от поверхности океана. Скорость распространения сигнала, умноженная на половину полученного временного отрезка, даёт искомое значение высоты h.
Рис.1.39. Геометрия спутникового нивелирования
Уровень поверхности океана (примерно соответствующий поверхности геоида) относительно центра масс Земли вычисляется как разность между высотой орбиты спутника, которая постоянно определяется станциями слежения, и значениями высоты полёта спутника над поверхностью океана.
Векторное уравнение спутникового нивелирования имеет вид
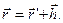
Из этого уравнения следует, во-первых, если при известном значении геоцентрического радиус-вектора r измерен вектор h, то можно определить геоцентрический радиус-вектор r¢ подспутниковой точки геоида; во-вторых, если задан геоид и измерен вектор h, то можно определить геоцентрический радиус-вектор спутникового высотомера.
Если же известны геоцентрические радиус-векторы, то можно предвычислить вектор h и сравнить его с измеренным значением. По совокупности разностей этих высот можно решать различные геодезические и геофизические задачи: эталонирование высотомеров, определение амплитуды волн океана и т.д.
Поверхность океана не совпадает с эквипотенциальной поверхностью гравитационного поля Земли из-за влияния различных астрономических, метеорологических, гидрологических и океанографических факторов, К числу этих факторов относятся приливные силы, изменения атмосферного давления и плотности воды. Последние в свою очередь зависят от температуры, солёности и давления. К ним же относятся изменения в выпадении осадков, притоке воды и её испарении.
Уклонения поверхности Мирового океана от геоида называют топографией морской поверхности. Изучение топографии морской поверхности – одна из главных задач физической океанографии. В геодезии она необходима для редуцирования измерений на единую уровенную поверхность.
Оперативное определение высот поверхности Мирового океана позволяет изучать топографию океана и периодически уточнять параметры внешнего гравитационного поля Земли. Повторные нивелировки дают представительскую статистику изменений геоида во времени и данные для решения координатно-гравитационной проблемы: установления на каждую эпоху геоцентрической системы геодезических координат и определения модели земного тяготения, ей соответствующей, и адекватной внешнему гравитационному полю Земли.
Поскольку около 70% общей площади поверхности Земли приходится на океан, значительная часть ранее не известных данных о гравитационном поле Земли, аппроксимированной в виде геоида, была получена спутниковым нивелированием. Для всей изученной части Мирового океана получены средние значения суммы высот геоида над эллипсоидом и высоты морской поверхности над геоидом по трапециям 1°´1° и 0,5°´0,5° с ошибкой, не превышающей ±1м. Альтиметрия даёт полезную информацию и при изучении рельефа морского дна. Наряду с обнаружением подводных горных хребтов, впадин и зон разломов альтиметрия даёт возможность выявлять подводные горы (к ним приурочены повышения геоида на несколько метров).
В будущем спутниковые наблюдения позволят с высокой точностью определять высоты ИСЗ над континентами. Используя совместно данные спутникового нивелирования над сушей и наземные астрономо-геодезические и гравиметрические измерения, можно будет определять геоид на континентах с ошибками порядка нескольких сантиметров с учётом движений земной коры и литосферных плит.
Вследствие неравномерного распределения масс в теле Земли сила тяжести на её поверхности изменяется по очень сложному закону. Задача о распределении силы тяжести на поверхности Земли была решена в общем виде в 18 веке французским математиком А. Клеро (1713-1765). Он впервые вывел формулу для вычисления силы тяжести на любой широте эллипсоида при известных значениях силы тяжести у полюса и на экваторе. Формула Клеро имеет вид


где 

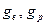




Гипотезы, на которых Клеро построил свою теорию, заключались в следующем. Земля внутри состоит из эллипсоидальных слоёв малого сжатия, имеющих общий центр и общую ось вращения. Каждый слой однороден, но от слоя к слою плотность меняется по произвольному закону, причём возможны скачкообразные изменения плотности от слоя к слою. Никаких предположений относительно агрегатного состояния каждого слоя, кроме наружного, не делается. Условие гидростатического равновесия должно быть соблюдено только для верхнего слоя. Верхний слой должен быть в жидком состоянии и действующая на него сила должна быть везде направлена по нормали к его внешней поверхности.
Теоретические исследования Клеро подтвердили, что фигура Земли связана с её внутренним строением. Они также показали, что результаты выводов о форме и размерах Земли, выполненных на основании опытных данных, совместно с определениями угловой скорости вращения Земли могут использоваться для изучения её внутреннего строения, а данные о внутреннем строении – для изучения фигуры Земли.
В пространственной геоцентрической системе координат потенциал притяжения для точки, находящейся на поверхности Земли или во внешнем пространстве, обычно представляется в виде разложения в бесконечный ряд по сферическим функциям Лежандра
V= 

где 



fM = f(M 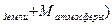
J 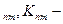
P 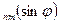
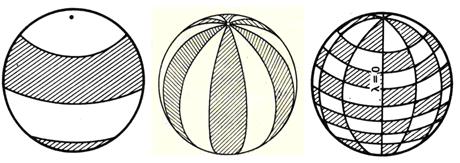
Рис.1.40. Положительные и отрицательные значения зональных, секториальных и тессеральных гармоник
В разложении (1.18) члены нулевого порядка (m=0) называются зональными гармониками, так как их значения изменяются только с широтой. Внутри одной зоны, отделённой от других с севера и с юга параллелями, зональные гармоники сохраняют свой знак (рис.1.40).
Гармоники называются секториальными, если их знак может изменяться только с долготой. Это имеет место при n=m. В этом случае шар оказывается расчленённым на сектора – полосы, которые соединяют северный и южный полюса. Внутри одного сектора секторальные гармоники сохраняют свой знак.
Гармоники, для которых 0 0 =. 
Нормальную часть поля силы тяжести можно рассчитать по формулам распределения нормальной силы тяжести. В Российской федерации наиболее часто используется формула немецкого геодезиста и геофизика Ф. Гельмерта (1843-1917), полученная им в 1901г.

В 1971г. Международный Геофизический и Геодезический союз принял следующую формулу для нормальной силы тяжести

В качестве Нормальной Земли принят общий земной эллипсоид с параметрами
Сжатие этого эллипсоида, определённое по спутниковым данным, равно 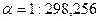
Существуют и другие формулы, учитывающие небольшое долготное изменение нормальной силы тяжести, а также асимметрию Северного и Южного полушарий. Ведётся подготовка к переходу к единой новой формуле с учётом уточнённого абсолютного значения силы тяжести.
Гравиметрическая изученность Земли весьма неравномерна. Материки исследованы более полно, чем моря и океаны, Северное полушарие в гравиметрическом отношении изучено лучше, чем Южное. Гравитационные аномалии на Земле, как правило, меньше 100мГал, их среднеквадратические вариации по Земле составляют около 20 мГал. Следовательно, гравитационное поле Земли достаточно гладкое. В Северном полушарии наибольшая величина средней квадратической аномалии составляет 27 мГал. В Южном полушарии, где значительную часть поверхности Земли занимает океан, гравитационное поле более спокойно. Максимальная аномалия силы тяжести на Земле зафиксирована на Гавайском архипелаге (+600 мГал).
В настоящее время создано достаточно много моделей гравитационного поля Земли разной детальности и точности. Они представляют собой некоторое приближение к реальному полю. Оптимальные модели наилучшим образом соответствуют результатам измерения силы тяжести, а также учитывают ошибки измерений и ошибки интерполяции. В глобальных моделях используют разложение по шаровым функциям, ограничиваясь их степенью. Наиболее детальная из известных моделей модель, получившая шифр EGM-96 (360´360).
Рис.1.41. Модель гравитационного поля Земли
На рис. 1.41 представлена модель гравитационного поля Земли, построенная по данным о небольших изменениях расстояния между двумя идентичными орбитальными спутниками GRACE (Gravity Recovery and Climate). Более тёмным цветом отмечены участки с повышенной гравитацией. Таковы, например, северная часть Срединно-Атлантического хребта в Атлантическом океане и Гималайские горы.
Глобальные модели гравитационного поля используются для решения задач для больших регионов земной поверхности (определение орбит ИСЗ, создание геофизических и геодинамических моделей). Глобальные модели гравитационного поля позволяют получать высоты геоида с точностью, достаточной для решения многих задач в науках о Земле, океанографии и навигации.
Для описания регионального поля часто используется модель степени и порядка 36 (36´36). Локальное описание гравитационного поля используется при создании геодезических сетей для задач высшей и прикладной геодезии, прикладной геофизики и геодинамики.
Представление потенциала притяжения Земли в виде ряда по сферическим функциям стало классическим. В силу простоты сферических функции оно очень удобно, однако оно обладает одним существенным недостатком, а именно медленной сходимостью. Это обстоятельство заставило искать другую форму представления потенциала.
С 1985г. наряду с моделями в виде гармонических коэффициентов геопотенциала создаются планетарные модели гравитационного поля в виде систем точечных масс. Впервые аномальная часть потенциала Земли была представлена потенциалом притяжения некоторой совокупности точечных масс в 1971г. Балмино. Им было использовано 126 материальных точек с заданными координатами в теле Земли. Такие модели дают возможность более оперативно выполнять некоторые геодезические, орбитальные и навигационные расчёты.
Рис.1.42. Карта высот геоида в системе модели геопотенциала GRIM3-L1
(сечение горизонталей 10 м)
Модели ПЗ-90 (до 36-й степени) и ГПЗ-200 (до 200-й степени) обеспечивают определение высот геоида со средней квадратической ошибкой соответственно 2,5 и 1,5м.
Вторые производные потенциала силы тяжести применяются при решении геодезических и геологоразведочных задач. Вертикальный градиент силы тяжести, соответствующий нормальной части гравитационного поля Земли, равен в среднем для всей Земли 3086 этвеш и изменяется от полюса к экватору всего на 0,1% своей величины. Намного меньше по абсолютной величине горизонтальные градиенты силы тяжести.
Рис.1.43. Внешний вид вариометра
Аномальная часть вторых производных потенциала даёт информацию о плотностных неоднородностях в верхних частях земной коры. По величине она достигает в равнинных местах десятков, а в горных – сотен этвеш. Вторые производные потенциала силы тяжести измеряются гравитационными вариометрами (рис.1.43).
Наибольшие искажения гравитационного поля Земли вызываются потенциалом притяжения Луны и Солнца. Это приводит к возникновению:
Лунный прилив геоида оценивается в 53,4см, а прилив, создаваемый Солнцем, составляет 24,6см. В общем, поверхность геоида колеблется в пределах 78см. Максимальное суммарное изменение силы тяжести под действием лунно-солнечных приливов равно 240 мкГал.
Изменения силы тяжести происходят и из-за перемещения центра инерции Земли в её теле. Изучение временных вариаций силы тяжести на гравиметрических пунктах, равномерно размещённых по всему земному шару, позволяет следить за положением центра масс в каждую эпоху.
Сила тяжести, измеряемая на поверхности Земли, содержит информацию о местоположении пункта наблюдений (геодезическое применение), распределении масс в недрах Земли (геофизическое применение) и, в случае повторных измерений, о временных изменениях в теле Земли (геодинамическое применение).
Как известно, основная задача геодезии состоит в определении поверхности Земли. Большинство измеряемых для этой цели величин в общем виде могут быть представлены как нелинейные функции векторов местоположения пункта наблюдений и визирной цели и гравитационного потенциала. Для получения из наблюдений геодезических координат пункта необходимо моделировать гравитационное поле. Системы высот в гравитационном поле Земли также предполагают, что характеристики этого поля известны. При определении гравитационного поля преобладают непосредственные определения вектора силы тяжести (направления отвесной линии и величины силы тяжести), а также её потенциала. По величинам силы тяжести, измеренным на поверхности Земли или редуцированным на неё, определяют геометрию этой поверхности.
Одна из задач физики Земли состоит в изучении твёрдой Земли (и других небесных тел) физическими методами, а также применении результатов для разработки статических и динамических моделей Земли. Важным источником информации для этого служат измеренные во внешнем пространстве элементы гравитационного поля, которые рассматриваются как функции распределения земных масс. Данные о гравитационном поле дают возможность определить функцию плотности (положение, форма и плотность аномальных масс). Для решения этой задачи используют аномалии силы тяжести. В меньшей степени используются другие параметры аномального поля.
При построении геодинамических моделей одним из наиболее важных условий является их соответствие реальному гравитационному полю. Временные вариации силы тяжести, обнаруженные из повторных измерений, дают важную информацию о глобальных, региональных и локальных перемещениях земных масс.
Глобальные изменения силы тяжести (область проявления более 10 4 км) могут быть вызваны смещениями эксцентричного земного ядра относительно мантии, перемещениями масс в мантии (конвекция в мантии) и литосфере (движение тектонических плит), а также повышением уровня Мирового океана.
Смещения масс и связанные с ними изменения силы тяжести вызываются и человеческой деятельностью (откачка воды, нефти, газа, горные разработки, создание крупных инженерных сооружений). Выемка близповерхностных масс приводит к возникновению внутренних компенсационных процессов, связанных с уплотнением осадочных пород или разрушением горных пород, что в свою очередь вызывает опускание дневной поверхности. При многолетней эксплуатации нефтяных и газовых месторождений опускания дневной поверхности могут составлять порядка дециметра в год. При откачке подземных вод понижающиеся водные горизонты в большинстве случаев образуют конические формы. В районах с уплотняющимися осадочными породами это приводит к необратимым опусканиям дневной поверхности, охватывающим обширные территории (в г. Мехико более 9м). Обычно мониторинг изменений силы тяжести в районах таких опусканий показывает увеличение силы тяжести
Изменения силы тяжести, вызванные внутренними геодинамическими процессами, представляют особый интерес. Изменения, связанные с землетрясениями и вулканизмом, являются предвестниками этих явлений. Измерения, выполненные до и после активной фазы этих явлений, важны для разработки динамических моделей накопления и разрядки напряжений при землетрясениях, а также моделей миграции вещества магмы и вариаций плотности в вулканах.
Изменения силы тяжести тектонического происхождения можно ожидать особенно на границах литосферных плит, они также содержат информацию о перемещениях масс под литосферой. В районах послеледникового поднятия земной коры или её опускания измеренные вариации позволяют судить о реологии (вязкости) верхней мантии.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет