Что такое нейрон в нейросети
Нейронные сети в картинках: от одного нейрона до глубоких архитектур
Многие материалы по нейронным сетям сразу начинаются с демонстрации довольно сложных архитектур. При этом самые базовые вещи, касающиеся функций активаций, инициализации весов, выбора количества слоёв в сети и т.д. если и рассматриваются, то вскользь. Получается начинающему практику нейронных сетей приходится брать типовые конфигурации и работать с ними фактически вслепую.
В статье мы пойдём по другому пути. Начнём с самой простой конфигурации — одного нейрона с одним входом и одним выходом, без активации. Далее будем маленькими итерациями усложнять конфигурацию сети и попробуем выжать из каждой из них разумный максимум. Это позволит подёргать сети за ниточки и наработать практическую интуицию в построении архитектур нейросетей, которая на практике оказывается очень ценным активом.
Иллюстративный материал
Популярные приложения нейросетей, такие как классификация или регрессия, представляют собой надстройку над самой сетью, включающей два дополнительных этапа — подготовку входных данных (выделение признаков, преобразование данных в вектор) и интерпретацию результатов. Для наших целей эти дополнительные стадии оказываются лишними, т.к. мы смотрим не на работу сети в чистом виде, а на некую конструкцию, где нейросеть является лишь составной частью.
Фреймворк
Для демонстрации конфигураций и результатов предлагаю взять популярный фреймворк Keras, написанный на Python. Хотя вы можете использовать любой другой инструмент для работы с нейросетями — чаще всего различия будут только в наименованиях.
Самая простая нейросеть
Самой простой из возможных конфигураций нейросетей является один нейрон с одним входом и одним выходом без активации (или можно сказать с линейной активацией f(x) = x):
N.B. Как видите, на вход сети подаются два значения — x и единица. Последняя необходима для того, чтобы ввести смещение b. Во всех популярных фреймворках входная единица уже неявно присутствует и не задаётся пользователем отдельно. Поэтому здесь и далее будем считать, что на вход подаётся одно значение.
Несмотря на свою простоту эта архитектура уже позволяет делать линейную регрессию, т.е. приближать функцию прямой линией (часто с минимизацией среднеквадратического отклонения). Пример очень важный, поэтому предлагаю разобрать его максимально подробно.
Как видите, наша простейшая сеть справилась с задачей приближения линейной функции линейной же функцией на ура. Попробуем теперь усложнить задачу, взяв более сложную функцию:
Опять же, результат вполне достойный. Давайте посмотрим на веса нашей модели после обучения:
Первое число — это вес w, второе — смещение b. Чтобы убедиться в этом, давайте нарисуем прямую f(x) = w * x + b:
Усложняем пример
Хорошо, с приближением прямой всё ясно. Но это и классическая линейная регрессия неплохо делала. Как же захватить нейросетью нелинейность аппроксимируемой функции?
Давайте попробуем накидать побольше нейронов, скажем пять штук. Т.к. на выходе ожидается одно значение, придётся добавить ещё один слой к сети, который просто будет суммировать все выходные значения с каждого из пяти нейронов:
И… ничего не вышло. Всё та же прямая, хотя матрица весов немного разрослась. Всё дело в том, что архитектура нашей сети сводится к линейной комбинации линейных функций:
f(x) = w1′ * (w1 * x + b1) +… + w5′ (w5 * x + b5) + b
Т.е. опять же является линейной функцией. Чтобы сделать поведение нашей сети более интересным, добавим нейронам внутреннего слоя функцию активации ReLU (выпрямитель, f(x) = max(0, x)), которая позволяет сети ломать прямую на сегменты:
Максимальное количество сегментов совпадает с количеством нейронов на внутреннем слое. Добавив больше нейронов можно получить более точное приближение:
Дайте больше точности!
Уже лучше, но огрехи видны на глаз — на изгибах, где исходная функция наименее похожа на прямую линию, приближение отстаёт.
В качестве стратегии оптимизации мы взяли довольно популярный метод — SGD (стохастический градиентный спуск). На практике часто используется его улучшенная версия с инерцией (SGDm, m — momentum). Это позволяет более плавно поворачивать на резких изгибах и приближение становится лучше на глаз:
Усложняем дальше
Синус — довольно удачная функция для оптимизации. Главным образом потому, что у него нет широких плато — т.е. областей, где функция изменяется очень медленно. К тому же сама функция изменяется довольно равномерно. Чтобы проверить нашу конфигурацию на прочность, возьмём функцию посложнее:
Увы и ах, здесь мы уже упираемся в потолок нашей архитектуры.
Дайте больше нелинейности!
Давайте попробуем заменить служивший нам в предыдущих примерах верой и правдой ReLU (выпрямитель) на более нелинейный гиперболический тангенс:
Инициализация весов — это важно!
Приближение стало лучше на сгибах, но часть функции наша сеть не увидела. Давайте попробуем поиграться с ещё одним параметром — начальным распределением весов. Используем популярное на практике значение ‘glorot_normal’ (по имени исследователя Xavier Glorot, в некоторых фреймворках называется XAVIER):
Уже лучше. Но использование ‘he_normal’ (по имени исследователя Kaiming He) даёт ещё более приятный результат:
Как это работает?
Давайте сделаем небольшую паузу и разберёмся, каким образом работает наша текущая конфигурация. Сеть представляет из себя линейную комбинацию гиперболических тангенсов:
f(x) = w1′ * tanh(w1 * x + b1) +… + w5′ * tanh(w5 * x + b5) + b
На иллюстрации хорошо видно, что каждый гиперболический тангенс захватил небольшую зону ответственности и работает над приближением функции в своём небольшом диапазоне. За пределами своей области тангенс сваливается в ноль или единицу и просто даёт смещение по оси ординат.
За границей области обучения
Давайте посмотрим, что происходит за границей области обучения сети, в нашем случае это [-3, 3]:
Как и было понятно из предыдущих примеров, за границами области обучения все гиперболические тангенсы превращаются в константы (строго говоря близкие к нулю или единице значения). Нейронная сеть не способна видеть за пределами области обучения: в зависимости от выбранных активаторов она будет очень грубо оценивать значение оптимизируемой функции. Об этом стоит помнить при конструировании признаков и входных данный для нейросети.
Идём в глубину
До сих пор наша конфигурация не являлась примером глубокой нейронной сети, т.к. в ней был всего один внутренний слой. Добавим ещё один:
Можете сами убедиться, что сеть лучше отработала проблемные участки в центре и около нижней границы по оси абсцисс:
N.B. Слепое добавление слоёв не даёт автоматического улучшения, что называется из коробки. Для большинства практических применений двух внутренних слоёв вполне достаточно, при этом вам не придётся разбираться со спецэффектами слишком глубоких сетей, как например проблема исчезающего градиента. Если вы всё-таки решили идти в глубину, будьте готовы много экспериментировать с обучением сети.
Количество нейронов на внутренних слоях
Просто поставим небольшой эксперимент:
Начиная с определённого момента добавление нейронов на внутренние слои не даёт выигрыша в оптимизации. Неплохое практическое правило — брать среднее между количеством входов и выходов сети.
Нейронные сети, перцептрон
Искусственная нейронная сеть (ИНС) (англ. Artificial neural network (ANN)) — упрощенная модель биологической нейронной сети, представляющая собой совокупность искусственных нейронов, взаимодействующих между собой.
На данный момент нейронные сети используются в многочисленных областях машинного обучения и решают проблемы различной сложности.
Содержание
Структура нейронной сети [ править ]
Хорошим примером биологической нейронной сети является человеческий мозг. Наш мозг — сложнейшая биологическая нейронная сеть, которая принимает информацию от органов чувств и каким-то образом ее обрабатывает (узнавание лиц, возникновение ощущений и т.д.). Мозг же, в свою очередь, состоит из нейронов, взаимодействующих между собой.
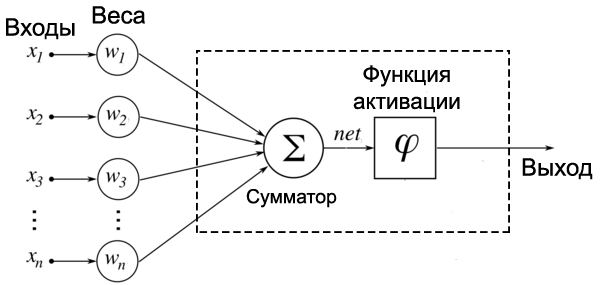
Для разных типов нейронов используют самые разные функции активации, но одними из самых популярных являются:
Виды нейронных сетей [ править ]
Разобравшись с тем, как устроен нейрон в нейронной сети, осталось понять, как их в этой сети располагать и соединять.
Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу — распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений. В остальном нейронные сети делятся на основные категории, представленные ниже.
Однослойные нейронные сети [ править ]
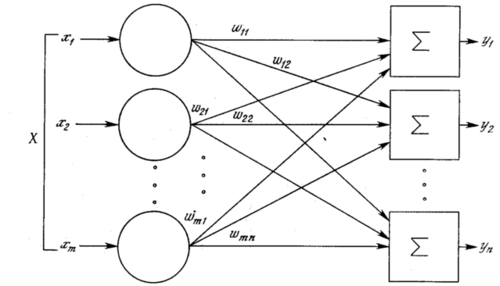
Однослойная нейронная сеть (англ. Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.
Как видно из схемы однослойной нейронной сети, представленной справа, сигналы [math]x_1, x_2, \ldots x_n[/math] поступают на входной слой (который не считается за слой нейронной сети), а затем сигналы распределяются на выходной слой обычных нейронов. На каждом ребре от нейрона входного слоя к нейрону выходного слоя написано число — вес соответствующей связи.
Многослойные нейронные сети [ править ]
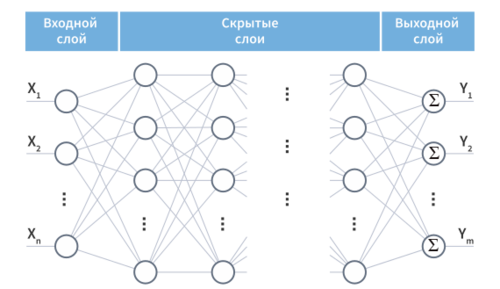
Многослойная нейронная сеть (англ. Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.
Помимо входного и выходного слоев эти нейронные сети содержат промежуточные, скрытые слои. Такие сети обладают гораздо большими возможностями, чем однослойные нейронные сети, однако методы обучения нейронов скрытого слоя были разработаны относительно недавно.
Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям на станках. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.
Сети прямого распространения [ править ]
Сети прямого распространения (англ. Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.
Все сети, описанные выше, являлись сетями прямого распространения, как следует из определения. Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.
Однако сигнал в нейронных сетях может идти и в обратную сторону.
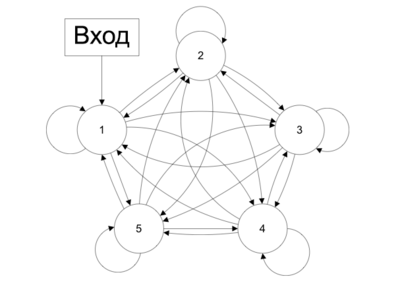
Сети с обратными связями [ править ]
Сети с обратными связями (англ. Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.
В сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах. В сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).
Обучение нейронной сети [ править ]
Обучение нейронной сети — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.
Это определение «обучения нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей, каждая из которых в отдельности состоит из нейронов одного типа (с одинаковой функцией активации). Наш мозг обучается благодаря изменению синапсов — элементов, которые усиливают или ослабляют входной сигнал.
Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ», а как только мы подадим немного измененный сигнал, вместо правильного ответа получим бессмыслицу. Мы ждем от сети способности обобщать какие-то признаки и решать задачу на различных входных данных. Именно с этой целью и создаются обучающие выборки.
Обучающая выборка — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.
После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике. Однако прежде чем сразу использовать нейронную сеть, обычно производят оценку качества ее работы на так называемой тестовой выборке.
Тестовая выборка — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.
Перцептрон [ править ]
Перцептрон (англ. Perceptron) — простейший вид нейронных сетей. В основе лежит математическая модель восприятия информации мозгом, состоящая из сенсоров, ассоциативных и реагирующих элементов.
История [ править ]
Идею перцептрона предложил нейрофизиолог Фрэнк Розенблатт. Он предложил схему устройства, моделирующего процесс человеческого восприятия, и назвал его «перцептроном» (от латинского perceptio — восприятие). В 1960 году Розенблатт представил первый нейрокомпьютер — «Марк-1», который был способен распознавать некоторые буквы английского алфавита.
Таким образом перцептрон является одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.
Описание [ править ]
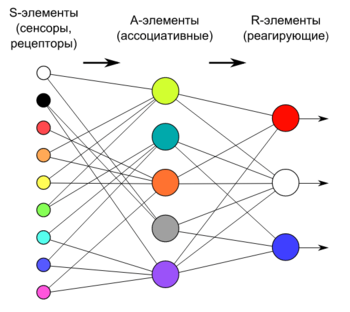
В основе перцептрона лежит математическая модель восприятия информации мозгом. Разные исследователи по-разному его определяют. В самом общем своем виде (как его описывал Розенблатт) он представляет систему из элементов трех разных типов: сенсоров, ассоциативных элементов и реагирующих элементов.
Принцип работы перцептрона следующий:
Для элементов перцептрона используют следующие названия:
Классификация перцептронов [ править ]
Перцептрон с одним скрытым слоем (элементарный перцептрон, англ. elementary perceptron) — перцептрон, у которого имеется только по одному слою S, A и R элементов.
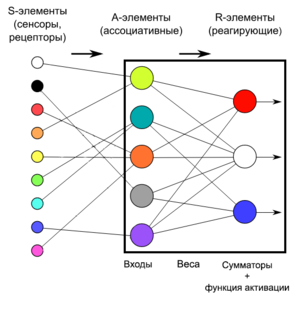
Однослойный персептрон (англ. Single-layer perceptron) — перцептрон, каждый S-элемент которого однозначно соответствует одному А-элементу, S-A связи всегда имеют вес 1, а порог любого А-элемента равен 1. Часть однослойного персептрона соответствует модели искусственного нейрона.
Его ключевая особенность состоит в том, что каждый S-элемент однозначно соответствует одному A-элементу, все S-A связи имеют вес, равный +1, а порог A элементов равен 1. Часть однослойного перцептрона, не содержащая входы, соответствует искусственному нейрону, как показано на картинке. Таким образом, однослойный перцептрон — это искусственный нейрон, который на вход принимает только 0 и 1.
Однослойный персептрон также может быть и элементарным персептроном, у которого только по одному слою S,A,R-элементов.
Многослойный перцептрон по Розенблатту (англ. Rosenblatt multilayer perceptron) — перцептрон, который содержит более 1 слоя А-элементов.
Многослойный перцептрон по Румельхарту (англ. Rumelhart multilater perceptron) — частный случай многослойного персептрона по Розенблатту, с двумя особенностями:
Обучение перцептрона [ править ]
Иначе говоря, мы минимизируем суммарное отклонение наших ответов от правильных, но только в неправильную сторону; верный ответ ничего не вносит в функцию ошибки. Умножение на [math]y(x)[/math] здесь нужно для того, чтобы знак произведения всегда получался отрицательным: если правильный ответ −1, значит, перцептрон выдал положительное число (иначе бы ответ был верным), и наоборот. В результате у нас получилась кусочно-линейная функция, дифференцируемая почти везде, а этого вполне достаточно.
Алгоритм такой — мы последовательно проходим примеры [math]x_1, x_2, \ldots[/math] из обучающего множества, и для каждого [math]x_n[/math] :
Ошибка на примере [math]x_n[/math] при этом, очевидно, уменьшается, но, конечно, совершенно никто не гарантирует, что вместе с тем не увеличится ошибка от других примеров. Это правило обновления весов так и называется — правило обучения перцептрона, и это было основной математической идеей работы Розенблатта.
Применение [ править ]
Примеры кода [ править ]
Пример использования с помощью scikit-learn [4] [ править ]
Нейронные сети для начинающих. Часть 2
Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.
Что такое нейрон смещения?
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
Для чего нужен нейрон смещения?

Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу H1, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес H1, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = H1*w1+H2*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Как сделать чтобы НС давала правильные ответы?
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
Что такое градиентный спуск?
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Что такое Метод Обратного Распространения (МОР)?
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1.


Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.
O1output = 0.33
O1ideal = 1
Error = 0.45
δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для H1:
H1output = 0.61
w5 = 1.5
δO1 = 0.148
δH1 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так: 
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:
H1output = 0.61
δO1 = 0.148
GRADw5 = 0.61 * 0.148 = 0.09
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом: 
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.
E = 0.7
Α = 0.3
w5 = 1.5
GRADw5 = 0.09
Δw5(i-1) = 0
Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + Δw5 = 1.563
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для H2.
GRADw6 = 0.69 * 0.148 = 0.1
Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.
H2input = 1 * 0.73 + 0 * 0.124 = 0.73
H2output = sigmoid(0.73) = 0.675
Результат — 0.37, ошибка — 39%.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Что еще нужно знать о процессе обучения?
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.
Что такое гиперпараметры?
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
Что такое сходимость?

Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
Что такое переобучение?
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.