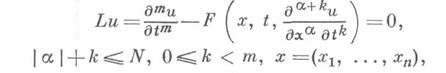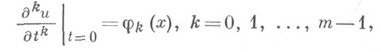Что такое начальные условия

НАЧАЛЬНЫЕ УСЛОВИЯ

— условия при постановке задачи Коши для дифференциальных уравнений. Для обыкновенного дифференциального уравнения, разрешенного относительно старшей производной:

Н. у. состоят в задании производных (данных Коши)

где — произвольная фиксированная точка области определения функции F;эта точка наз. начальной точкой искомого решения. Задачу Коши (1), (2) часто наз. также начальной задачей.

Для дифференциального уравнения с частными производными, записанного в нормальной форме относительно выделенной переменной V.

Н. у. состоят в задании производных (данные Коши):

от искомого решения и( х, t )этого уравнения на гиперплоскости t=0 (носителя начальных условий).

Смотреть что такое «НАЧАЛЬНЫЕ УСЛОВИЯ» в других словарях:

начальные условия — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] начальные условия Начальное состояние в динамических моделях экономики — совокупность сложившихся к началу… … Справочник технического переводчика

Начальные условия — [initial conditions] (начальное состояние) в динамических моделях экономики совокупность сложившихся к началу исследуемого (или планового) периода значений экономических переменных, последующие значения которых определяются в ходе решения задачи … Экономико-математический словарь

Начальные условия — В теории дифференциальных уравнений, начальные и граничные условия дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой… … Википедия

начальные условия — [initial conditions] описание состояния тела перед деформацией. Обычно в начальный момент заданны эйлеровы координаты точек xi0 поверхности тела, напряжения, скорости, плотности, температуры в любой точке М тела. Дия области пространства,… … Энциклопедический словарь по металлургии

начальные условия — pradinės sąlygos statusas T sritis Standartizacija ir metrologija apibrėžtis Sąlygos, apibūdinančios sistemą vyksmo pradžioje. atitikmenys: angl. initial conditions; starting conditions vok. Anfangsbedingungen, f rus. исходные условия, n;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

начальные условия — pradinės sąlygos statusas T sritis chemija apibrėžtis Sąlygos, apibūdinančios sistemą proceso pradžioje. atitikmenys: angl. initial conditions; starting conditions rus. исходные условия; начальные условия … Chemijos terminų aiškinamasis žodynas

начальные условия — pradinės sąlygos statusas T sritis fizika atitikmenys: angl. initial conditions; starting conditions vok. Anfangsbedingungen, f rus. исходные условия, n; начальные условия, n pranc. conditions initiales, f … Fizikos terminų žodynas

Независимые начальные условия — Независимые начальные условия электрические параметры, которые не изменяются скачком в момент коммутации, то есть, остаются неизменными в начале переходного процесса в электрической цепи. Согласно законам коммутации, скачком не могут… … Википедия

Начальные и граничные условия — В теории дифференциальных уравнений, начальные и граничные условия дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе… … Википедия

Начальные и краевые условия — В теории дифференциальных уравнений, начальные и граничные условия дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой… … Википедия

Источник

Начальные и граничные условия

Раздел №3. Математическая постановка краевых задач

Уравнение теплопроводности (диффузии) является дифференциальным уравнением в частных производных относительно функции двух переменных T(x,t). Пространственную переменную x будем считать изменяющейся на ограниченном отрезке [0,l], а время – . Уравнение теплопроводности имеет первый порядок по времени и второй порядок по пространственной координате x. (Такие уравнения называются уравнениями параболического типа). Так же как и обыкновенное дифференциальное уравнение, где искомая функция зависит от одной переменной, уравнение в частных производных имеет бесконечное множество частных решений. В теории обыкновенных дифференциальных уравнений для выделения нужного частного решения задаются дополнительные условия – начальные или граничные. Точно так же для нахождения нужного частного решения уравнения в частных производных должны быть заданы аналогичные условия. При этом, поскольку искомая функция зависит от двух переменных, эти дополнительные условия должны быть заданы по каждой переменной. Дополнительные условия по времени называются начальными условиями, а дополнительные условия по пространственной координате называются граничными условиями, вместе их называют краевыми условиями. Поскольку уравнение (2.5) имеет первый порядок по времени, то начальное условие только одно, и записывается оно в виде значения искомой функции в начальный момент времени

. (2.6)

Относительно дополнительных условий по пространственной координате x имеется гораздо большее разнообразие. А именно, существует три типа граничных условий: граничные условия 1-го, 2-го, 3-го рода. Сформулируем все три типа для одномерного уравнения теплопроводности и диффузии.

Граничные условия 1-го рода. В этом случае, на границе области, где изучается процесс, задается значение искомой функции (температуры или концентрации)

В одномерном случае граница состоит из двух частей, задаваемых уравнениями x=0 и x=l, поэтому граничные условия запишутся так

или ,

где f1(t), f2(t) — заданные функции времени, а .

Граничные условия 2-го рода. Здесь на границе области задается не сама искомая функция, а ее тепловой или диффузионный поток. (т.е. в случае граничных условий 2-го рода задается производная искомой функции по направлению внешней нормали к поверхности). В соответствии с законами Фурье и Нернста граничное условие 2-го рода для одномерного случая имеет вид (отдельно для теплопроводности и диффузии)

и (2.7)

Граничные условия первого и второго рода называются однородными, если они равны нулю.

Физически однородные граничные условия второго рода означают тепловую изоляцию поверхности или ее непроницаемость для диффундирующего вещества.

Граничные условия 3-го рода. Это условие тепло- или массообмена с окружающей средой. Для теплопроводности процесс теплообмена описывается законом Ньютона – Рихмана, согласно которому количество теплоты, которое отдает или получает малый участок поверхности DS за малое время Dt, пропорционально разности температур поверхности и окружающей среды, т.е.

, (2.9)

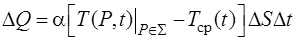
где α – относительный коэффициент теплообмена [α] = [кал/(см2 сек град)], – точка на границе области.

С другой стороны, количество теплоты, которое переносится через тот же участок DS за то же время Dt определяется законом Фурье

.

или

,

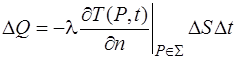
где – коэффициент теплообмена [h] = [1/см].

В одномерном случае это будет

.

Однородные граничные условия третьего рода, когда температура окружающей среды равна нулю, имеют вид

.

Для диффузии граничные условия третьего рода записываются аналогично

.

Соответственно однородные граничные условия третьего рода, когда концентрация вещества в окружающей среде равна нулю, имеют вид

.

Ранее выведенные основные уравнения теплопроводности (диффузии) содержат пространственную переменную x и время t. Для этих уравнений рассмотрим модельные задачи на примере тонкого стержня или бесконечной пластины, когда 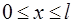. В краевую задачу входят следующие составляющие:

· уравнение теплопроводности вместе с областью определения уравнения по пространственным переменным и времени, причем только во внутренних точках областей для x и t;

· начальное условие для области по x берется из эксперимента;

· граничные условия при x = 0, x = l берутся из эксперимента.

Источник

Начальные условия

В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.

Обычно дифференциальное уравнение имеет не одно решение, а целое их семейство. Начальные и граничные условия позволяют выбрать из него одно, соответствующее реальному физическому процессу или явлению. В теории обыкновенных дифференциальных уравнений доказана теорема существования и единственности решения задачи с начальным условием (т. н. задачи Коши). Для уравнений в частных производных получены некоторые теоремы существования и единственности решений для определенных классов начальных и краевых задач.

Содержание

Терминология

Иногда к граничным относят и начальные условия в нестационарных задачах, таких как решение гиперболических или параболических уравнений.

Для стационарных задач существует разделение граничных условий на главные и естественные.

Естественные условия содержат также и производную решения по нормали к границе.

Пример

Корректность постановки граничных условий

Задачи математической физики описывают реальные физические процессы, а потому их постановка должна удовлетворять следующим естественным требованиям:

Требование непрерывной зависимости решения обусловливается тем обстоятельством, что физические данные, как правило, определяются из эксперимента приближенно, и поэтому нужно быть уверенным в том, что решение задачи в рамках выбранной математической модели не будет существенно зависеть от погрешности измерений. Математически это требование можно записать, например, так (для независимости от свободного члена):

Пусть задано два дифференциальных уравнения: с одинаковыми дифференциальными операторами и одинаковыми граничными условиями, тогда их решения будут непрерывно зависеть от свободного члена, если:

решения соответствующих уравнений.

Множество функций, для которых выполняются перечисленные требования, называется классом корректности. Некорректную постановку граничных условий хорошо иллюстрирует пример Адамара.

См. также

Литература

Владимиров В.С., Жаринов В.В. Уравнения математической физики. — Физматлит, 2004. — ISBN 5-9221-0310-X

Полезное

Смотреть что такое «Начальные условия» в других словарях:

начальные условия — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] начальные условия Начальное состояние в динамических моделях экономики — совокупность сложившихся к началу… … Справочник технического переводчика

Начальные условия — [initial conditions] (начальное состояние) в динамических моделях экономики совокупность сложившихся к началу исследуемого (или планового) периода значений экономических переменных, последующие значения которых определяются в ходе решения задачи … Экономико-математический словарь

начальные условия — [initial conditions] описание состояния тела перед деформацией. Обычно в начальный момент заданны эйлеровы координаты точек xi0 поверхности тела, напряжения, скорости, плотности, температуры в любой точке М тела. Дия области пространства,… … Энциклопедический словарь по металлургии

начальные условия — pradinės sąlygos statusas T sritis Standartizacija ir metrologija apibrėžtis Sąlygos, apibūdinančios sistemą vyksmo pradžioje. atitikmenys: angl. initial conditions; starting conditions vok. Anfangsbedingungen, f rus. исходные условия, n;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

начальные условия — pradinės sąlygos statusas T sritis chemija apibrėžtis Sąlygos, apibūdinančios sistemą proceso pradžioje. atitikmenys: angl. initial conditions; starting conditions rus. исходные условия; начальные условия … Chemijos terminų aiškinamasis žodynas

начальные условия — pradinės sąlygos statusas T sritis fizika atitikmenys: angl. initial conditions; starting conditions vok. Anfangsbedingungen, f rus. исходные условия, n; начальные условия, n pranc. conditions initiales, f … Fizikos terminų žodynas

НАЧАЛЬНЫЕ УСЛОВИЯ — условия при постановке задачи Коши для дифференциальных уравнений. Для обыкновенного дифференциального уравнения, разрешенного относительно старшей производной: Н. у. состоят в задании производных (данных Коши) где произвольная фиксированная… … Математическая энциклопедия

Независимые начальные условия — Независимые начальные условия электрические параметры, которые не изменяются скачком в момент коммутации, то есть, остаются неизменными в начале переходного процесса в электрической цепи. Согласно законам коммутации, скачком не могут… … Википедия

Начальные и граничные условия — В теории дифференциальных уравнений, начальные и граничные условия дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе… … Википедия

Начальные и краевые условия — В теории дифференциальных уравнений, начальные и граничные условия дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой… … Википедия

Источник

Начальные и граничные условия

Здравствуйте, продолжаем нашу рубрику по дифференциальным уравнениям, это уже 2 статья, если вы хотите начать сначала и ознакомиться с видами дифференциальных уравнений, то вам в первую статью.

Введение

Итак, для использования численных методов при решении дифференциального уравнения необходимо дополнительные условия. Если искомая функция(концентрация, температура и т.д) является функцией времени u=u(t), то требуются начальные условия, которые являются значением этой функции в момент времени, принятый за начальный:

Если начальная функция также зависит и от пространственных координат u=u(t,x), то начальное условие характеризуют ее распределение в пространстве в начальный момент времени:

В последнем случае помимо начальных условий требуются еще и граничные условия, которые имеют значения функции u(t,x) на границе изучаемой системы для любого момента времени. Причем, если искомая функция зависит от нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них.

Небольшой пример

Например для следующего уравнения:

Сразу же возникает вопрос, почему именно так? Так вот, порядок производной определяет количество граничных условий для переменной. Как вы заметили, по y присутствует только первая производная, поэтому и одно граничное условие.

Классификация граничных условий

Для лучшего понимания рассмотрим классификацию на примере уравнения:

Записываются следующим образом:

Здесь вместо самих функций используются их первые производные.

В этом случае левое и правое граничные условия могут быть разных родов:

Заключение

На этом мы подходим к концу нашей статьи. Сегодня мы с вами изучили начальные и граничные условия в дифференциальных уравнениях. Если вам что то осталось непонятным, то это нормально, не пугайтесь. В будущих статьях мы будем еще подробнее разбираться с этими и другими тонкостями, ну а на сегодня это все.

Спасибо, что прочитали статью, если у вас остались вопросы, то задавайте их в комментариях.
И, буду вам очень признателен, если вы вступите в нашу группу вконтакте, ссылка на которую размещена слева вверху под названием сайта.

Источник

Начальные и краевые условия

В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.

Обычно дифференциальное уравнение имеет не одно решение, а целое их семейство. Начальные и граничные условия позволяют выбрать из него одно, соответствующее реальному физическому процессу или явлению. В теории обыкновенных дифференциальных уравнений доказана теорема существования и единственности решения задачи с начальным условием (т. н. задачи Коши). Для уравнений в частных производных получены некоторые теоремы существования и единственности решений для определенных классов начальных и краевых задач.

Содержание

Терминология

Иногда к граничным относят и начальные условия в нестационарных задачах, таких как решение гиперболических или параболических уравнений.

Для стационарных задач существует разделение граничных условий на главные и естественные.

Естественные условия содержат также и производную решения по нормали к границе.

Пример

Корректность постановки граничных условий

Задачи математической физики описывают реальные физические процессы, а потому их постановка должна удовлетворять следующим естественным требованиям:

Требование непрерывной зависимости решения обусловливается тем обстоятельством, что физические данные, как правило, определяются из эксперимента приближенно, и поэтому нужно быть уверенным в том, что решение задачи в рамках выбранной математической модели не будет существенно зависеть от погрешности измерений. Математически это требование можно записать, например, так (для независимости от свободного члена):

Пусть задано два дифференциальных уравнения: с одинаковыми дифференциальными операторами и одинаковыми граничными условиями, тогда их решения будут непрерывно зависеть от свободного члена, если:

решения соответствующих уравнений.

Множество функций, для которых выполняются перечисленные требования, называется классом корректности. Некорректную постановку граничных условий хорошо иллюстрирует пример Адамара.

См. также

Литература

Владимиров В.С., Жаринов В.В. Уравнения математической физики. — Физматлит, 2004. — ISBN 5-9221-0310-X

Полезное

Смотреть что такое «Начальные и краевые условия» в других словарях:

Краевые условия — В теории дифференциальных уравнений, начальные и граничные условия дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой… … Википедия

Краевые задачи — задачи, в которых из некоторого класса функций, определённых в данной области, требуется найти ту, которая удовлетворяет на границе (крае) этой области заданным условиям. Функции, описывающие конкретные явления природы (физические,… … Большая советская энциклопедия

АДСОРБЦИЯ — (от лат. ad на, при и sorbeo поглощаю), изменение (обычно повышение) концентрации в ва вблизи пов сти раздела фаз ( поглощение на пов сти ). В общем случае причина А. нескомпенсированность межмол. сил вблизи этой пов сти, т. е. наличие адсорбц.… … Химическая энциклопедия

МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ — уравнения, описывающие математические модели физических явлений. М. ф. у. часть предмета математической физики. Многие явления физики и механики (гидро и газодинамики, упругости, электродинамики, оптики, теории переноса, физики плазмы, квантовой… … Математическая энциклопедия

МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ — ур ния, описывающие матем. модели физ. явлений. Теория этих моделей (математическая физи к а) занимает промежуточное положение между физикой и математикой. При построении моделей используют физ. законы, однако методы исследования полученных ур… … Физическая энциклопедия

СМЕШАННАЯ И КРАЕВАЯ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ — задачи отыскания решений уравнений и систем с частными производными гиперболич. типа, удовлетворяющих на границе области их задания (или ее части) определенным условиям (см. Краевые условия, Начальные условия). Краевая задача для гиперболич.… … Математическая энциклопедия

Принцип максимума (уравнение теплопроводности) — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия

КОШИ ЗАДАЧА — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в отыскании решения (интеграла) дифференциального уравнения, удовлетворяющего так наз. начальным условиям (начальным данным). К. з. обычно… … Математическая энциклопедия

Уравнение диффузии — Механика сплошных сред … Википедия

Источник