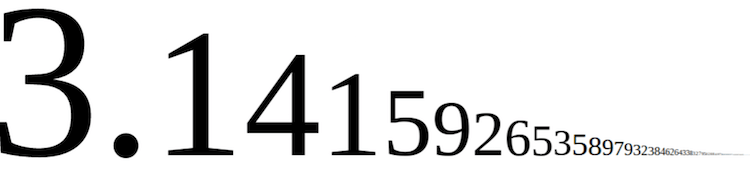Что такое на самом деле число пи
Число Пи — это математическая постоянная
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы подробно расскажем, что такое число «пи», которое частенько используется в математике.
На самом деле, это постоянная величина, которая помогала еще древним Египтянам проводить расчеты при проектировании. Она, например, позволяла, зная диаметр окружности, легко рассчитать ее длину (периметр).
Но вот только значение этой постоянной в те времена точно рассчитать не получалось. Сегодня же мы можем узнать чему равно число ПИ вплоть до триллионного знака после запятой.
Что такое число Пи
Впервые школьники сталкиваются с этим понятием еще в 3-м классе, когда начинают изучать окружность (что это?).
Им просто говорят, что какую бы окружность они не нарисовали, если поделить ее длину на диаметр, то получится одно и то же число. И называется это число «пи», обозначается латинской буквой «π» и равно 3,14.
Кстати, именно так и звучит официальное определение числа «пи»:
Пи – это математическая константа (постоянная), которая равна отношению длины окружности к ее диаметру.
А вот в 6-м классе школьников ближе знакомят с этим числом. Именно тогда начинают изучать формулы длины и площади окружности. А в них без «пи» не обойтись:
История возникновения числа «пи»
Ученые считают, что еще в Древнем Египте знали о существовании некой математической постоянной. Этот вывод сделали на основании папирусов, на которых расписаны вычисления площади круга. И в ней фигурировало некое число, которое равнялось 3,160.
Но число, напоминающее «пи» встречается и в других странах:
Эта греческая буква взята неслучайно, она первая в словах «περιφέρεια» (окружность) и «περίμετρος» (периметр).
И наконец, общепринятым понятие «математической постоянной» стало в 1737 году после публикации научных работ Леонардо Эйлера.
Чему равно число Пи
Количество знаков после запятой у числа «пи» бесконечно.
Во всяком случае, ни один компьютер (это что?) до сих пор так и не смог вычислить их до конца. Самая современная вычислительная машина смогла показать лишь 10 триллионов цифр.
И что наиболее любопытно, в этом огромном количестве цифр нет никакой зависимости или тенденции. Математики очень любят разбивать знаки после запятой на группы по 10 цифр. И вот среди этих групп у числа «пи» невозможно найти две одинаковые.
На рисунке ниже приведено значение числа Пи с точностью до 1000 знаков после запятой:
Число «пи» в фольклоре
Чтобы запомнить побольше знаков числа «пи» люди пользуются разными приемами мнемотехники.
Например, есть такие стихотворения:
Чтобы нам не ошибиться,
Надо правильно прочесть.
Три, четырнадцать, пятнадцать.
Девяносто два и шесть.
А есть специальные стихи, в которых числа определяются по количеству букв в словах:
Это(3) я(1) знаю(4) и(1) помню(5) прекрасно(9).
Пи(2) многие(6) знаки(5) мне(3) лишни(5), напрасны(8).
Доверимся(9) знаньям(7) громадным(9)
Тех(3), пи(2) кто(3) сосчитал(8), цифр(4) армаду(6).
Называние «пи» присутствует и в нескольких фильмах. Например, в 1998 году режиссер Даррен Аронофски снял картину «Пи». Это психологический триллер, в котором главный герой считает, что все в жизни можно описать с помощью чисел. Но в результате он чуть не сошел с ума.
А в 2012 году на экраны вышел фильм «Жизнь Пи». Он, правда, не имеет ничего общего с математикой. Это приключенческая лента о путешествиях индийского юноши по имени Пи.
С 1987 году математики даже отмечают День числа «пи». Происходит это 14 марта, так энтузиасты обыграли первые цифры (3,14). А начало торжеств приходится на определенное время – 01:59. Это также дань цифрам, которые идут после запятой.
Празднования проходят, как правило, скромно. Люди просто готовят круглый торт, садятся за круглый стол и делятся забавными историями, связанными с числом «пи» и математическими задачками в целом.
И наконец, есть даже анекдоты на тему числа «пи». Один из таких звучит так:
Один ученый спрашивает другого:
— Скажи, а почему рельсы прямые, колеса круглые, а когда поезд едет, то они стучат?
— Ну, это просто. Колеса же круглые. А значит, их площадь равна «пи эр квадрат». Вот тот самый квадрат и стучит.
Вот и все, что мы хотели рассказать о числе «пи». До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (3)
Приведенное выше число пи не точное (приближенное)
ТОчное значение этого числа 3,14269680. Это доказано в статье «Через центр масс квадранта к числу пи» см. в Инете
Самое забавное, что мы не можем вычислить точную площадь круга, именно потому что число Пи бесконечно.
Вроде бы Архимед нашел свое число Пи следующим образом, он брал два многоугольника, один был вписан в окружность, а сама окружность была вписана во второй многоугольник, затем он находил периметры этих двух многоугольников и брал их отношение, потом он увеличивал количество сторон этих многоугольников и они все больше становились похожи на окружность, так он и получил наиболее точное значение своего числа.
Да зачем нужны эти триллионы после запятой? Вот учёным делать нечего, всё равно погрешность изготовления окружности будет выше этой точности.
Что особенного в числе Пи?
Буквально через 2 недели дату своего рождения празднует знаменитое число Пи. Про него говорят ученые, продолжают снимать фильмы и безудержно используют в высшей математике. Праздник для универсального числа пройдёт 14 марта в 1.59.26 ночи. Знатокам математики не трудно разгадать, почему именно этот весенний день считается именитым. А тем, кто не знают, но хочет получить ответ на загадку, узнать особенности числа Пи – наша статья в помощь.
Перед тем, как перейти к основным вопросам давайте ознакомимся с самым длинным числом. В 2011 году американскому учёному удалось вновь установить мировой рекорд и вычислить количество знаков числа Пи до 10 триллионов. Прежний рекорд был установлен тем же американским и японским экспертами, но количество знаков составляло 5 триллионов. Конечно ни один математик не сможет запомнить последовательность 10 триллионов цифр. Да и необходимости в этом нет. Для вычисления окружности с диаметром достаточно знать 39 цифр.
Число Пи история.
Знак Пи интересные особенности.
Интересный факт:
В марте 2011 года американский музыкант Майкл Блэйк решил создать из числа Пи мелодию. Он положил его на музыку. Чтобы эксперимент прошёл успешно, композитор взял 31 цифру после запятой. Распределил ноты для каждой, правда пришлось залезть в соседнюю октаву. С помощью квинтового круга назначил каждой цифре собственный аккорд. Провёл аранжировку мелодии в темпе 157 ударов в минуту. Получилась весьма интересная и бурная мелодия. Найти ее можно в любом интернет источнике.
Число Пи, что такое? Его краткая история
Число Пи знак математической константы. Он приравнивает отношение длины окружности к длине ее диаметра. Обозначать данное число названием «Пи» предложил британский математик Джонс в 1706 году. А уже в 1737 году число Пи приняло форму официального названия благодаря учёному математику Леонарду Эйлеру.
Но на самом деле значение существует уже больше 4000 лет. Ведь древнеегипетские математики подтвердили, что длина окружности к диаметру одинаковые для любой окружности. Значение равно чуть больше трёх.
Архимед, Хэн, Ариабхата – математические эксперты, которые на протяжение многих лет приближали число Пи к точному значению. Но самую приближённую цифру открыл китайский математик Цзу Чунчжи в 480-ых годах. На тот период число имело около 10 символов после запятой. Голландцу Людольфу удалось назвать ещё 20 знаков. Он потратил на это 20 лет жизни. Позже археологи нашли его дневник, в котором было указано следующие 15 чисел. На 1500 год значение Пи имело уже 35 цифр.
Как только в мире появились компьютерные системы, значение резко стало увеличиваться. Количество символов после запятой доросло до триллионов.
Число Пи, особенности и факты
Часто задаваемые вопросы про Пи значение
Станьте членом КЛАНА и каждый вторник вы будете получать свежий номер «Аргументы Недели», со скидкой более чем 70%, вместе с эксклюзивными материалами, не вошедшими в полосы газеты. Получите премиум доступ к библиотеке интереснейших и популярных книг, а также архиву более чем 700 вышедших номеров БЕСПЛАТНО. В дополнение у вас появится возможность целый год пользоваться бесплатными юридическими консультациями наших экспертов.
Таинственное число «ПИ»
Что такое «пи» известно абсолютно всем. Но знакомое всем со школы число возникает во многих ситуациях, не имеющим никакого отношения к окружностям. Его можно встретить в теории вероятностей, в формуле Стирлинга для вычисления факториала, в решении задач с комплексными числами и прочих неожиданных и далеких от геометрии областях математики. Английский математик Август де Морган назвал как-то «пи» “…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу”.
Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта (в американском написании – 3.14) ровно в 01:59 дата и время совпадут с первыми разрядами числа Пи = 3,14159.
14 марта 1879 года также родился создатель теории относительности Альберт Эйнштейн, что делает этот день еще более привлекательным для всех любителей математики.
Кроме того, математики отмечают и день приближенного значения Пи, который приходится на 22 июля (22/7 в европейском формате записи даты).
«В это время читают хвалебные речи в честь числа Пи и его роли в жизни человечества, рисуют антиутопические картины мира без Пи, едят пироги с изображением греческой буквы Пи или с первыми цифрами самого числа, решают математические головоломки и загадки, а также водят хороводы», – пишет Википедия.
В цифровом выражении Пи начинается как 3,141592 и имеет бесконечную математическую продолжительность.
Французский ученый Фабрис Беллар вычислил число Пи с рекордной точностью. Об этом сообщается на его официальном сайте. Свежий рекорд составляет около 2,7 триллиона (2 триллиона 699 миллиардов 999 миллионов 990 тысяч) десятичных знаков. Предыдущее достижение принадлежит японцам, которые посчитали константу с точностью до 2,6 триллиона десятичных знаков.
На вычисления у Беллара ушло около 103 дней. Все расчеты проводились на домашнем компьютере, стоимость которого лежит в пределах 2000 евро. Для сравнения, предыдущий рекорд был установлен на суперкомпьютере T2K Tsukuba System, у которого ушло на работу около 73 часов.
Сначала Пи рассчитывалось в двоичной системе, после чего переводилось в десятичную. Это проделали за 13 дней. В общей сложности для хранения всех цифр требуется 1,1 терабайта дискового пространства.
Более того, до сих пор не известно, все ли цифры от 0 до 9 встречаются в десятичной записи числа Пи бесконечное число раз.
В данном случае сверхточное вычисление числа является удобным экспериментом, результаты которого позволяют сформулировать гипотезы относительно тех или иных особенностей числа.
Число вычисляется по определенным правилам, причем при любом вычислении, в любом месте и в любое время, на определенном месте в записи числа стоит одна и та же цифра. Значит существует некий закон, по которому в числе в определенном месте ставится определенная цифра. Конечно, это закон не простой, но закон всё таки есть. И, значит, цифры в записи числа не случайны, а закономерны.
Считают число Пи: PI = 4 — 4/3 + 4/5 — 4/7 + 4/9 — … — 4/n + 4/(n+2)
Поиск Pi или деление столбиком:
Пары целых чисел, дающих при делении большое приближение к числу Pi. Деление производилось «столбиком», чтобы обойти ограничения по длине чисел с плавающей точкой Visual Basic 6.
Pi = 3.14159265358979323846264>33832795028841 971.
К экзотическим методам вычисления пи вроде использования теории вероятности или простых чисел принадлежит и метод, придуманный Г.А. Гальпериным, и называемый Пи-биллиардом, который основан на оригинальной модели. При столкновении двух шаров, меньший из которых находится между большим и стенкой, и больший движется к стенке, число соударений шаров позволяет вычислить Пи со сколь угодно большой наперед заданной точностью. Надо только запустить процесс (можно и на компьютере) и посчитать число ударов шаров. Программная реализация этой модели пока не известна
В каждой книге по занимательной математике вы непременно найдете историю вычисления и уточнения значения числа «пи». Сначала, в древних Китае, Египте, Вавилоне и Греции для расчетов использовали дроби, например, 22/7 или 49/16. В Средние века и Эпоху Возрождения европейские, индийские и арабские математики уточнили значение «пи» до 40 знаков после десятичной точки, а к началу Эпохи Компьютеров усилиями многих энтузиастов количество знаков было доведено до 500. Такая точность имеет чисто научный интерес (об этом ниже), для практики, в пределах Земли достаточно 11 знаков после точки.
Число объясняет мир
Кажется, двум американским математикам удалось приблизиться к разгадке тайны числа пи, представляющего в сугубо математическом плане соотношение длины окружности круга к его диаметру, сообщает Der Spiegel.
Как иррациональная величина оно не может быть представлено в виде завершенной дроби, поэтому после запятой следует бесконечный ряд цифр. Это свойство всегда привлекало математиков, стремившихся найти, с одной стороны, более точное значение пи, а с другой — его обобщенную формулу.
Однако математики Дэвид Бейли из лаборатории Lawrence Berkeley National Laboratory в Калифорнии и Ричард Грендел из колледжа Reed College в Портланде, рассматривали число с другой стороны — они попытались найти какой-то смысл в кажущемся хаотичном ряду цифр после запятой. В результате установили, что регулярно повторяются комбинации следующих цифр — 59345 и 78952.
Но пока что не могут ответить на вопрос, является ли повторение случайным или закономерным. Вопрос закономерности повторения определенных комбинаций цифр, и не только в числе пи,— один из самых трудных в математике. Но теперь можно сказать что-то более определенное об этом числе. Открытие прокладывает путь к разгадке числа пи и в целом к определению его сути — является ли оно нормальным для нашего мира или нет.
Интересные данные о распределении цифр Пи.
(Программирование — величайшее из достижений человечества. Благодаря ему мы регулярно узнаем то, что нам знать совсем не нужно, но уж очень интересно)
Посчитано (для миллиона цифр после запятой):
В первых 200,000,000,000 десятичных знаках Пи цифры встречались с такой частотой:
01234567891 : с 26,852,899,245
01234567891 : с 41,952,536,161
01234567891 : с 99,972,955,571
01234567891 : с 102,081,851,717
01234567891 : с 171,257,652,369
01234567890 : с 53,217,681,704
Можно поискать в первых десяти тысячах знаков Пи свой телефон или дату рождения, если не получится, то ищите в 100.000 знаков.
В числе 1/Пи начиная с 55,172,085,586 знака идут 3333333333333, не правда ли удивительно?
В философии обычно противопоставляют случайное и необходимое. Так знаки числа пи случайны? Или они необходимы? Скажем, третий знак числа пи равен «4». И вне зависимости от того, кто-бы это пи вычислял, в каком месте и в какое время он бы это не делал, третий знак с необходимостью всегда будет равен «4».
Связь числа Пи, числом Фи и рядом Фибоначии. Связь числа 3,1415916 и числа 1,61803 и последовательности Пизанского.
А нам-то что с того? А следует из этого то, что в десятичном хвосте числа пи можно отыскать любую задуманную последовательность цифр. Ваш телефон? Пожалуйста, и не раз (проверить можно тут, но имейте в виду, что эта страничка весит около 300 мегабайт, так что загрузки придется подождать. Можно скачать жалкий миллион знаков тут или поверить на слово: любая последовательность цифр в десятичных знаках числа пи рано или поздно найдется. Любая!
Для более возвышенных читателей можно предложить и другой пример: если зашифровать все буквы цифрами, то в десятичном разложении числа пи можно найти всю мировую литературу и науку, и рецепт изготовления соуса бешамель, и все священные книги всех религий. Я не шучу, это строгий научный факт. Ведь последовательность БЕСКОНЕЧНА и сочетания не повторяются, следовательно она содержит ВСЕ сочетания цифр, и это уже доказано. А раз все, то все. В том числе и такие, которые соответствуют выбранной вами книге.
А это опять-таки означает, что там содержится не только вся мировая литература, которая уже написана (в частности и те книги, которые сгорели и т.д.), но и все книги, которые еще БУДУТ написаны.
Получается, что это число (единственное разумное число во вселенной!) и управляет нашим миром.
Вопрос в том, как их там отыскать.
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.
Но Сатана не долго ждал реванша.
Суть: число Пи не равно 3,14159265358979.
Это заблуждение, основанное на ошибочном постулате отождествления плоского Евклидового пространства с реальным пространством Вселенной.
Краткое объяснение почему в общем случае Пи не равно 3,14159265358979.
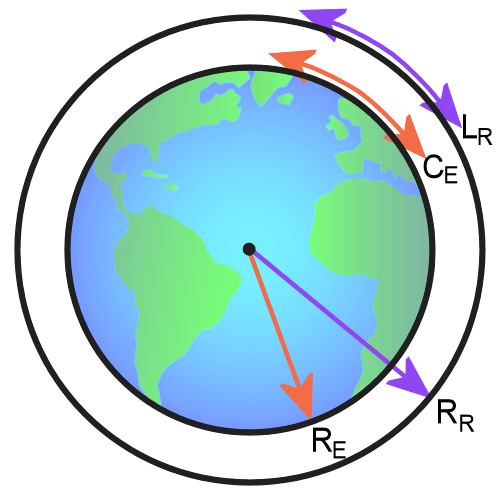
Этот феномен связан с кривизной пространства. Силовые линии во Вселенной на значительных расстояниях не идеальные прямые, а слегка изогнутые линии. Мы уже доросли до момента констатации факта, что в реальном мире не существует идеально прямых линий, идеально плоских кругов, идеального Евклидового пространства. Следовательно, мы должны представлять себе любой круг одного радиуса на сфере гораздо большего радиуса.
Мы заблуждаемся, думая что пространство плоско, «кубично». Вселенная не кубична, не цилиндрична и тем более не пирамидальна. Вселенная сферична. Единственный случай, когда плоскость может быть идеальной (в смысле «неизогнутой») является случай, когда такая плоскость проходит через центр Вселенной.
Конечно, кривизной CD-ROMа можно пренебречь, поскольку диаметр компакт-диска значительно меньше диаметра Земли, тем более диаметра Вселенной. Но пренебрегать кривизной в орбитах комет и астероидов не следует. Неистребимое Птолемеевское убеждение, что мы всё ещё находимся в центре Вселенной может нам дорого стоить.
Ниже приводятся аксиомы плоского Евклидова («кубичного» Декартова) пространства и сформулированная мной дополнительная аксиома для сферического пространства.
Аксиомы плоского сознания:
через 1 точку можно провести бесконечное количество прямых и бесконечное количество плоскостей.
через 2 точки можно провести 1 и только 1 прямую, через которую можно провести бесконечное количество плоскостей.
через 3 точки в общем случае нельзя провести ни одной прямой и одну, и только одну, плоскость. Дополнительная аксиома для сферического сознания:
через 4 точки в общем случае нельзя провести ни одной прямой, ни одной плоскости и одну и только одну сферу. Арсентьев Алексей Иванович
Немного мистики. Число ПИ Разумно?
На самом деле, Кэнтор лукавит, ответ есть, просто он настолько невероятен, что учёные предпочитают не выносить его на широкую публику, опасаясь за собственную жизнь (об этом чуть позже): число Пи само себя контролирует, оно разумно! Вздор? Не спешите. Ведь ещё Фонвизин говорил, что «в человеческом невежестве весьма утешительно считать всё то за вздор, чего не знаешь.»
Связана ли эта история с числом Пи? Пока неясно, но не правда ли, любопытно?
Вообще говоря, подобных историй можно накопать очень много, и, разумеется, не все они трагичны.
Но, перейдём к «во-вторых»: каким образом число вообще может быть разумным? Да очень просто. Человеческий мозг содержит 100 млрд. нейронов, число знаков Пи после запятой вообще стремится к бесконечности, в общем, по формальным признакам оно может быть разумным. Но ведь если верить работе американского физика Дэвида Бейли и канадских математиков Питера Борвина и Саймона Плофе, последовательность десятичных знаков в Пи подчиняется теории хаоса, грубо говоря, число Пи это и есть хаос в его первозданном виде. Может ли хаос быть разумным? Конечно! Точно так же, как и вакуум, при его кажущейся пустоте, как известно, отнюдь не пуст.
Но ведь год (1592) может определяться по собственному, более логичному для Пи летоисчислению. Если принять это предположение, то претендентов на роль числа Пи становится много больше.
В какой личности Пи персонифицировано сегодня, не ясно, но для того, что бы увидеть значение этого числа для нашего мира, не нужно быть математиком: Пи проявляется во всём, что нас окружает. И это, кстати, очень свойственно для любого разумного существа, каковым, без сомнения, является Пи!
-Пер-СОНальный ИДЕН-тифи-КА-ЦИ-онный номер.
Что такое число ПИ?
Расшифровка числа ПИ (3, 14. ) (пин-код), сделать это может любой и без меня, через Глаголицу. Подставляем вместо цифр буквы (числовые значения букв приведены в Глаголице) и получаем вот такую фразу: Глаголи (глаголю, говорю, делаю) Аз (я, ас, мастер, творец) Добро. А если взять следующие цифры, то там получается примерно следующее: «Делаю я добро, я есть Фита (скрытое, внебрачный ребенок, непорочное зачатие, непроявленное, 9), ведаю (познаю) искажение (зло) это есть говорение(действие) воля (желание) Земля делаю познаю делаю воля добро зло (искажение) познаю зло добро делаю». и так до бесконечности, там много цифр, но полагаю, что всё об одном и том же.
15 интересных фактов о числе Пи, о которых вы, возможно, не знали
Пи считается хлебом с маслом для математиков и инженеров. Это буквально круто, немного странно, но круто. Число Пи является математической константой, и оно определяет отношение между окружностью круга и его диаметром. С начала 19-го века (наиболее вероятно с середины 18-го века), это было обозначено греческой буквой «π». Это некоторые известные вещи о пи, но как насчет вещей, которые ты не знаешь? Хотите узнать некоторые неизвестные факты об этом интересном номере? Давайте наполним вас некоторыми интересными фактами о числе Пи.
11. Ваши банковские реквизиты можно найти в пи
Что ж, мы знаем, что число Пи является иррациональным числом, то есть его десятичное представление может длиться вечно. Технически, каждое возможное число, которое вы можете придумать, находится где-то в нем. Это включает в себя ваш контактный номер, дату рождения, номер вашего шкафчика и даже ваши банковские реквизиты. Более того, если у нас будет достаточно цифр, использование алгоритма, который может преобразовывать числа в буквы, позволит нам найти Библию, полное собрание сочинений Шекспира и Чосера или любую книгу, когда-либо написанную.
10. Использует в навигации
Пи играет важную роль в системах наведения, установленных на спутниках и космических станциях. Из всего, навигация в космосе на самом деле требует высокой точности. Для каждой вычисляемой десятичной цифры мы получаем большую точность. Но насколько мы должны быть точными, чтобы все работало правильно? Сьюзан Гомез из НАСА, управляющего Международной космической станцией по навигации, навигации и управлению (GNC), сообщает, что в большинстве расчетов с использованием Пи используются 15 цифр для GNC и 16 цифр для космической интегрированной системы глобального позиционирования / инерциальной навигационной системы (SIGI).
9. Истинная площадь круга никогда не может быть известна
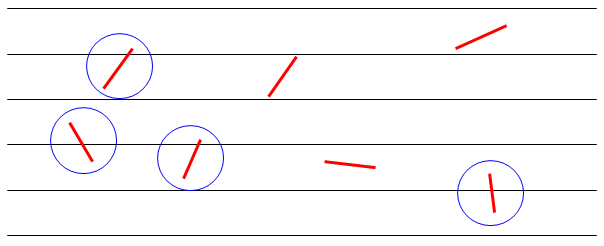
8. Игла Буффона
Игла Буффона или просто проблема с иглой в вероятности была впервые указана Жоржем-Луи Леклерком, графом де Буффоном, в 18-м веке, когда падение иглы на лист, отмеченный линиями, определит вероятность того, что игла пересечет линию на странице. Важно отметить, что вероятность результата эквивалентна значению числа Пи.
Давайте разберемся с этим. В этом случае на самом деле есть две переменные: угол наклона иглы, давайте присвоим ему символ тета (θ) и расстояние между ближайшей линией и центральной точкой иглы. Тета может варьироваться от 0 ° до 180 °, который измеряется параллельно нарисованным линиям.
Выяснилось, что вероятность того, что игла прорежет линию при посадке, составляет ровно 2 / Пи или почти 64%. Это означает, что число Пи можно как-то рассчитать, используя технику Буффона, если у кого-то будет достаточно времени и терпения, чтобы пройти все симуляции. Чтобы понять это намного лучше, вы можете попробовать это.
7. Отношения между извилистыми реками и Пи
У Пи неожиданные отношения со многими явлениями в этом мире, включая извилистые реки. Как? Что ж, путь любой реки в основном описывается ее извилистостью, способностью изгибаться, перемещаться назад и вперед по ее пойме. Математически говоря, это длина извилистого пути, деленная на длину реки от начала до конца. Оказывается, что средняя река имеет извилистость числа Пи независимо от ее длины или количества поворотов на своем пути.
6. Преобразование Фурье и обработка сигналов
Пи играет еще одну очень важную роль в области «обработки сигналов». Это просто анализ, синтез и модификация сигналов. Но здесь действует сложная система. Эта сложная система представляет собой «преобразование Фурье», которое преобразует сигналы в частотный спектр. Мобильный телефон каждого, будь то его андроид или iPhone, выполняет преобразование Фурье, когда он связывается с местной сотовой вышкой.
Кроме того, формула оценивается вашим мобильным телефоном в цифровом виде с помощью определенного алгоритма, известного как «быстрое преобразование Фурье» или «БПФ», который был открыт математиками в 1950-х годах. Важно отметить, что каждый процесс включает в себя число π. Так что технически, есть определенное значение Пи где-то в вашем телефоне, будь то простой или смартфон.
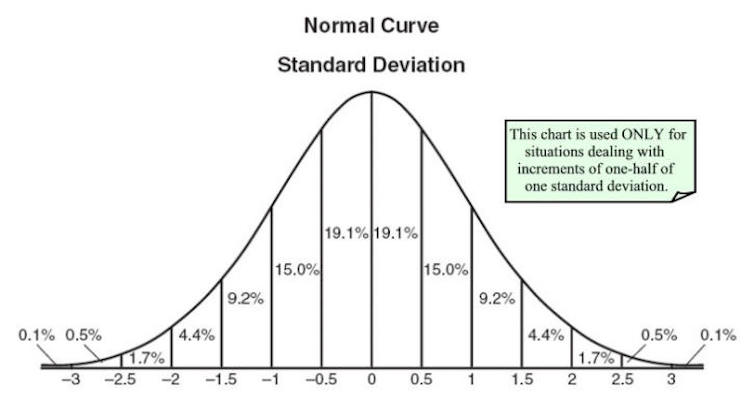
5. Распределение вероятностей
Пи также играет важную роль в нормальном распределении вероятностей. Без сомнения, вы сталкивались с таким распределением вероятностей не один, а много раз. Они важны и часто используются в различных областях исследований, включая математику, физику и общественные науки. Это то, что вам нужно, от прогнозирования результатов теста ученика до измерения отдаленных сверхновых звезд.
Это правило большого пальца: всякий раз, когда вы видите, как Пи подкрадывается где-то в любом уравнении, убедитесь, что где-то в этом спрятан круг. В этом случае Пи вводится через интеграл Эйлера – Пуассона, который содержит квадратный корень из Пи.
4. Проблема с лентой
Предположим, вы хотите обернуть вокруг Земли ленту на экваторе, длина окружности которого составляет 24 900 миль (идеальная сфера). Теперь попытайтесь выяснить, сколько потребуется ленты, которая могла бы окружить Землю на расстоянии одного дюйма над ее поверхностью. Можно легко подумать, что для этого потребуется огромное количество ленты. Но на самом деле это не так. Мы расскажем вам, как.
Еще раз предположив, что Земля является идеальной сферой, у нас будет круг с окружностью 24 900 миль (на экваторе). Это означает, что радиус будет 24 900 / (2 * пи) или примерно 3963 миль. Теперь вторая лента, на дюйм выше поверхности Земли, будет иметь радиус на один дюйм больше радиуса Земли, что дает нам уравнение C = 2 Пи (r + 1) или C = 2 Пи (r) + 2 Пи.
Отсюда можно сказать, что окружность второй ленты увеличится на 2Пи. Фактически, независимо от того, какой первоначальный радиус увеличивает радиус, всегда будет 2Пи.
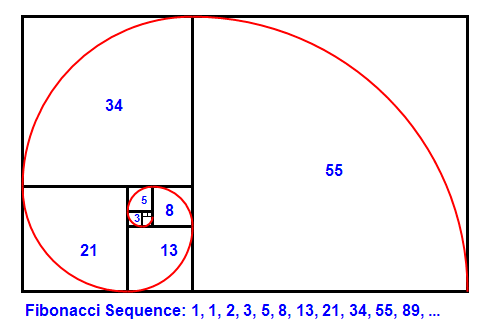
3. Последовательность Фибоначчи и вычисление числа Пи
Долгое время вычисления числа Пи основывались на двух методах: первый был разработан Архимедом, а второй был разработан Джеймсом Грегори, шотландским математиком в 1671 году. Однако оказывается, что последовательность Фибоначчи также может быть эффективно использована для вычисления значение Пи.
2. Самый первый расчет
Считается, что Пи был первоначально открыт древними вавилонянами около 4000 лет назад. Согласно Rhind Papyrus, древние египтяне вычислили значение Пи как приблизительно 3.1605. Но первый зарегистрированный метод для вычисления значения числа Пи был разработан греческим математиком Архимедом Сиракузским в 250 году до нашей эры.
Архимед знал о том факте, что он не обнаружил фактическое значение Пи, а лишь приблизительное значение в этих пределах. Таким образом, Архимед показал, что число Пи между 3 1/7 и 3 10/71. Этот алгоритм строго использовался учеными и инженерами на протяжении 1000 лет, из-за чего даже сегодня его иногда называют «постоянной Архимеда».
1. Скрытая связь между квантовой механикой и Пи
Физики недавно обнаружили связь между многовековой известной математической формулой Пи и квантовой механики, которая скрывалась годами. Это было в 1665 году, когда известный британский математик Джон Уоллис представил свою собственную версию формулы вычисления Пи. Исследователи из Университета Рочестера считают, что они нашли ту же формулу, скрывающуюся при расчете энергетических уровней атома водорода.
Краткие факты
С 1998 года, каждый год 14 марта, научное сообщество празднует день Пи. Этот конкретный день был выбран из-за его соответствия с 3.14, который является пи значение. Первое широко посещаемое празднование дня пи было организовано физиком Ларри Шоу. Интересно, что Альберт Эйнштейн родился 14 марта 1879 года.
В 2002 году группа японских исследователей из Токийского университета вычислила 1,24 триллиона цифр числа пи, используя мощный суперкомпьютер Hitachi SR 8000, побив все предыдущие рекорды.
По мнению некоторых математиков, вместо того чтобы называть его Безугловым, гораздо правильнее сказать, что круг имеет бесконечное число углов.