Что такое мощность алфавита
Что такое мощность алфавита
Алфавитом в информатике называется система знаков, с помощью которой можно подать информационное сообщение. Чтобы понять сущность этого определения, приведем немного дополнительных теоретических фактов:
Но на практике мы имеем следующее: компьютер не понимает, что такое буквы. Поэтому для передачи информационного сообщения его сначала нужно закодировать понятным компьютеру языком. Для того чтобы двигаться дальше, необходимо ввести дополнительные термины.
Что такое мощность алфавита
Под мощностью алфавита мы подразумеваем общее количество символов в нем. Для того чтобы узнать, какова мощность алфавита, необходимо просто посчитать количество символов в нем. Давайте разбираться. Для русского алфавита мощность алфавита равна 33 или же 32 символам, если не использовать «ё».
Давайте предположим, что все символы в нашем алфавите встречаются с равной вероятностью. Это предположение можно понимать так: допустим, у нас есть мешок с подписанными кубиками. Число кубиков в нем бесконечно, и каждый подписан лишь одним символом. Тогда при равномерном распределении, сколько бы мы кубиков ни доставали из мешка, количество кубиков с разными символами будет одинаково, или будет стремиться к этому при росте числа кубиков, которые мы достаем из мешка.
Оценка веса информационных сообщений
Почти сто лет назад американский инженер Ральф Хартли вывел формулу, с помощью которой можно оценивать количество информации в сообщении. Его формула работает для равновероятных событий и выглядит так:
Эта формула в общем виде задает связь между количеством равновероятных событий «M» и количеством информации «i».
Рассчитываем мощность
Скорее всего, вам уже известно из школьного курса информатики, что в современных вычислительных системах, построенных на архитектуре фон Неймана, используется двоичная система кодировки информации. Так кодируются как программы, так и данные.
Как измеряют информацию
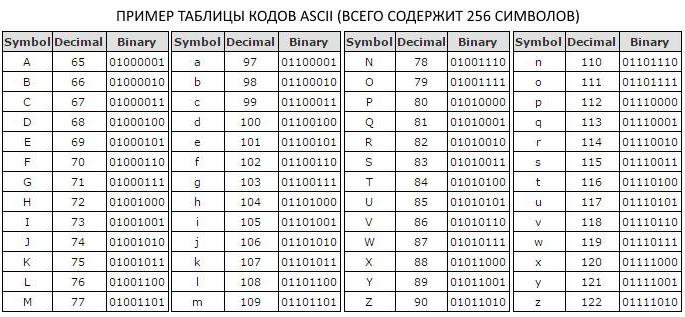
Восьмибитная кодировка текстовых сообщений, которая используется в кодовой таблице ASCII, позволяет вместить базовый набор символов латиницы и кириллицы в прописном и строчном варианте, цифры, символы знаков препинания и другие базовые символы.
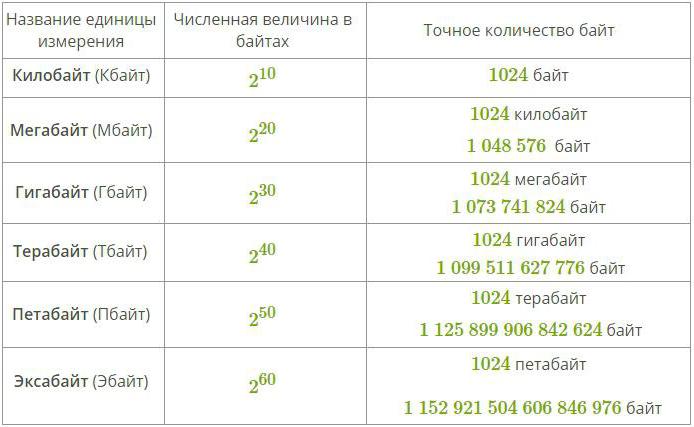
Для того чтобы измерять более крупные объемы данных, используют специальные приставки к словам байт и бит. Такие приставки приведены в таблице ниже:
Многие люди, изучавшие физику возразят, что рационально было бы использовать классические приставки для обозначения единиц информации (вроде кило- и мега-), но на самом деле это не совсем корректно, ведь такие префиксы к величинам обозначают умножение на ту или иную степень числа десять, когда в информатике везде используется двоичная система измерений.
Правильные названия единиц измерения данных
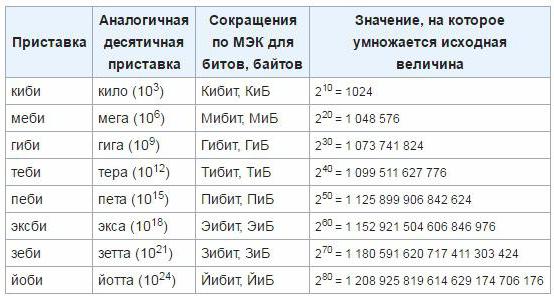
Для того чтобы устранить некорректности и неудобства, в марте 1999 года Международной комиссией в области электротехники были утверждены новые приставки к единицам, которые используются для определения объема информации в электронной вычислительной технике. Такими приставками стали «меби», «киби», «гиби», «теби», «эксби», «пети». Пока эти единицы еще не прижились, так что, скорее всего, необходимо время для введения этого стандарта и начала широкого применения. Как осуществлять переход от классических единиц к новоутвержденным, вы можете определить по следующей таблице:
Предположим, что мы имеем текст, который содержит K символов. Тогда, используя алфавитный подход, можно вычислить объем информации V, который в нем содержится. Он будет равен произведению мощности алфавита на информационный вес одного символа в нем.
По формуле Хартли мы знаем, как вычислить объем информации через двоичный логарифм. Предположив, что количество знаков алфавита равно N и количество знаков в записи информационного сообщения равняется K, получим такую формулу для вычисления информационного объема сообщения:
Алфавитный подход свидетельствует о том, что информационный объем будет зависеть только лишь от мощности алфавита и размера сообщений (то есть количества символов в нем), но никак не будет связан со смысловым содержанием для человека.
Примеры расчета мощности
На уроках информатики часто дают задачи на нахождение мощности алфавита, длины сообщения или информационного объема. Вот одна из таких задач:
«Текстовый файл занимает 11 Кбайт дискового пространства и содержит 11264 символа. Определите мощность алфавита данного текстового файла».
Каким будет решение, можно увидеть на картинке ниже.
Таким образом, алфавит мощностью 256 символов несет в себе всего лишь 8 бит информации, что в информатике называют одним байтом. Байт описывает 1 символ таблицы ASCII, что, если задуматься, совсем не много.
Современные хранилища данных вроде дата-центров Google и Facebook содержат не меньше, чем десятки петабайт информации. Точное количество данных, впрочем, трудно будет подсчитать даже им самим, ведь тогда нужно будет остановить все процессы на серверах и закрыть пользователям доступ к записи и редактированию их личной информации.
Но чтобы вообразить такие немыслимые объемы данных, необходимо четко понимать, что все складывается из маленьких деталей. Необходимо понимать, чему равна мощность алфавита (256) и сколько бит содержит 1 байт информации (как вы помните, 8).
Мощность алфавита в информатике
Описание термина
Понятие мощности алфавита находится в основании изучения информатики. Алфавитом принято называть набор многочисленных символов. Сумма всех их в определённом языке и есть алфавитная мощность. Иными словами, это количество всех символов, входящих в конкретно взятый язык. Сюда входят не только буквы, но и прочие обозначения, в частности:
Это определение считается обобщённым и не принимает во внимание вычисления информационной составляющей сообщения. Она может содержать в себе числа, знаки препинания и прочее. В этом случае прибегают к использованию другого способа. Его суть основывается на том, что любая буква, цифра или знак обладают собственным информационным объемом данных. Компьютер работает с этим информационным кодом и распознает то, что было написано.
Основным постулатом в информатике является тот факт, что устройство разбирает введённую информацию исключительно в двоичном коде в форме нуля и единицы. В итоге получается, что абсолютно любой символ алфавита может быть успешно закодирован при помощи соответствующего подбора этих двух цифровых символов. Самая маленькая последовательность, применяемая при обозначении какой-либо цифры, буквы или другого знака, состоит из двух элементов.
Информационная масса отдельно взятого символа обычно изображается в форме информационной стандартной измерительной единицы, которая называется «бит». Восемь битов становятся равны одному байту.
Отображение символов в двоичном коде
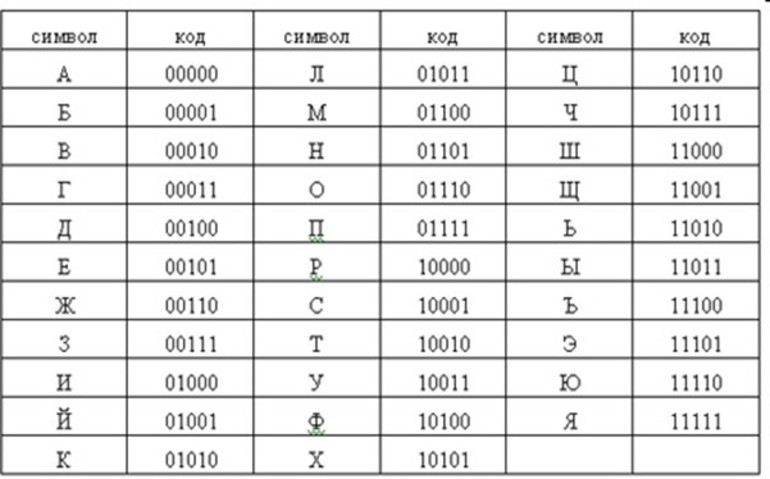
Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:
Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:
Иными словами, если алфавитная мощность равна 8, то вес отдельно взятого символа для двоичного трёхзначного кода составит 3 бита.
Вычисление мощности алфавита
Эта формула была изобретена американским инженером Ральфом Хартли более сотни лет тому назад. Она применяется для работы с равновероятными событиями и используется для определения мощности конкретного буквенного набора, которая обозначается буквой N (информационная масса или объём). n означает численность бит в словесной единице, иными словами, количество знаков внутри двоичного кода. Так, если n равен 1, то N тоже равен 1, при n = 2 N = 4, при n = 3 N = 8, при n = 4 N = 16.
Чтобы сформулировать теорию о численности информации в набранном словосочетании, пользуются формулой I=K*i. В этом случае К обозначает численность всех символов в предложении, а i — это информационная масса символа.
При ответе на вопрос, как найти мощность алфавита, нужно сказать, что в русском языке 33 буквы, поэтому это можно выразить как N = 33. Для сравнения, аналогичный показатель в английском, немецком и французском языках равняется 26, в испанском — 27. Венгерский язык, например, является 40-символьным.
Существует также и клавиатурный язык, куда входят не только буквы, но и дополнительные знаки. Так, в русском языке есть ещё 10 цифр и 11 символов, а также пробел и пара скобок. Их мощность прибавляется к аналогичному буквенному показателю, и на выходе получается N = 33+10+11+1+2=57. В некоторых случаях букву «ё» не выделяют в качестве отдельного самостоятельного символа, и в таком случае полная мощность русского алфавита становится равна 56.
Определение информационного объёма в тексте
Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:
По всем расчётам получается, что мощность компьютерного алфавита составляет 256 различных символов и вариантов. В соответствии с формулой Хартли, N = 256, а i — масса любого из значков в клавиатурном алфавите соответствует одному байту, или восьми битам.
Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.
Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.
В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.
Для удобства их всегда переводят в увеличенные величины — кило-, мега-, гигабайты и прочее. Для их упрощённого обозначения используются специальные сокращения: Кб, Мб, Гб и так далее. 1 Кб равняется 1024 байтам (2 байта в десятой степени), 1 Мб составляет 1024 Кб (2 Кб в десятой степени) и так далее. Исходя из этого, 65250 байт будут составлять 63,72 килобайта.
Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.
При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.
Примеры расчёта мощности
От пользователей или обучающихся в задачах часто требуют научиться определять информационный объём какого-либо сообщения, приняв информационный вес символа за один байт. Так, в отрывке из поэмы Н. Н. Некрасова «Крестьянские дети»:
Я из лесу вышел; был сильный мороз»
будет 67 символов вместе с пробелами, то есть, в соответствии с условиями задания, 67 байт. Их количество умножают на 8 (количество битов в байте), и на выходе получается 536 битов.
Таким образом, зная в теории суть мощности, можно без проблем определять информационный объем различных сообщений.
Мощность алфавита: что это и как она определяется?

Методы измерения информации в электронном виде
Мощность алфавита может пригодиться очень многим пользователям в процессе работы. Однако перед тем как дать определение этому термину и разобраться в методах его расчета необходимо немного поговорить о том, как измеряется электронная информация, поскольку это является материальной базой, на основании которой базируется дальнейшая теория.
Каждый человек знает о том, что любая величина имеет свою систему измерений. Например, температура измеряется в градусах, расстояние выражается в метрах, временные интервалы строятся из секунд и так далее. Однако немногие пользователи знают о том, в каких величинах измеряется текстовая информация в электронном виде. Для этих целей в информатике и было создано определение мощность алфавита.
Определение термина
Исходя из того, что значение абсолютно любой величины, известной в наши дни человечеству, является неким параметром, состоящим из набора измерительных единиц, то определение понятию мощности алфавита проще всего сделать следующим образом: мощность алфавита — это количество символов, которое входит в состав любого языка.
Однако это всего-лишь общее определение, которое отражает только поверхностное значение мощности алфавита, поскольку само определение носит более глубокий характер. Чтобы понять всю его суть необходимо разобраться с тем, что представляют собой символы, с точки зрения высоких технологий. Все символы, используемые в компьютере, включают в себя буквы, цифры, знаки препинания и набор специальных символов. Однако это еще не все, поскольку для определения мощности алфавита необходимо еще учитывать и пробел, который предназначен для разделения слов между собой.
Давайте в качестве примера рассмотрим русскую раскладку клавиатуры, которая используется для печати русскоязычного текста и состоит из 34 букв, 10 цифр и 11 дополнительных символов, суммарное количество которых составляет 54, что, в свою очередь, классифицируется как мощность алфавита русской раскладки клавиатуры..
Информационный вес символов
Давайте постепенно продвигаться далее. Мощность алфавита не заключается в одном лишь числе букв и цифр, которые используются в напечатанном тексте. Для определения этого параметра необходим более глубокий подход.
Давайте на секунду задумаемся о том, какой минимальный объем символов входит в состав одной буквы, цифры или специального знака? Правильный ответ — два. Каждый символ в компьютере обладает своим информационным весом, благодаря которому машина способна распознавать какую информацию ввел пользователь. Все дело в том, что машина не способна распознавать информацию в том виде, в котором ее представляют люди. Вместо этого, он использует специальный машинный язык, состоящий из нулей и единиц, при помощи которых происходит преобразование текстовой информации в двоичный код, понятный компьютерной системе.
Что касается информационного веса, то он выражается в битах и является стандартной единицей для измерения информации в электронном виде.
Немного о двоичном коде
Теперь мы имеем более-менее доступным для понимания определением мощности алфавита. Однако для понимания всей глубины теории представления электронной информации машинами необходимо иметь представление о двоичном коде. Давайте рассмотрим этот вопрос на примере мощности алфавита, состоящей из четырех любых символов, каждый из которых имеет вес два бита.
Следуя из всего вышесказанного, четыре символа будут иметь весь четыре бита, восемь — три и так далее. На основании этого принципа и происходит расчет веса текстовой информации, выраженной в электронном виде, компьютерными системами.
Вычисления мощности алфавита и ее практическое использование
С терминологией и основными теоретическими терминами мы разобрались, поэтому теперь давайте рассмотрим какая существует взаимосвязь между мощностью алфавита и его весом. Чтобы более наглядно провести взаимосвязь между ними давайте рассмотрим одну формулу: N=2b, в которой первая переменная соответствует количеству символов, а вторая — количеству знаков, используемых компьютерами в машинном языке.
Из этого математического выражения следует, что 21=2, 22=4, 23=8, 24=16 и так далее. На основании этого можно сделать весьма разумный и обоснованный вывод: число символов, используемых в машинном языке, представляет собой вес символа.
Как измеряется объем информации?
Рассмотренные выше примеры являются очень простыми, на примере которых можно дать общее представление мощности алфавита. Однако на деле все выглядит намного сложнее, поскольку каждый пользователь в процессе набора текста использует не только строчные, но и заглавные буквы, а также различные шрифты, языковую раскладку, знаки препинания, специальные символы, цвета и многое другое. Исходя из этого можно предположить, что общее число всех суммарных символов равняется 256. Поскольку 256 равняется 28 в двоичном коде, то в этом случае вес каждого символа составляет 8 битам или одному байту.
Таким образом, обладая всеми необходимыми параметрами, мы можем рассчитать объем электронной информации. Например, мы напечатали 30 страниц печатной информации, на каждой из которых содержится 50 строк по 60 различных символов. Используя известную нам формулу, производим необходимые вычисления:
— информационный вес одной строки будет равен: 50 х 60 = 3000 байт;
— а весь текст будет весить: 3000 х 50 = 150 000 байт.
Стоит отметить, что конечный результат можно выражать не только в байтах, а переводить стандартную единицу измерения в килобайты, мегабайты и другие. Для этого необходимо величину более младшего порядка разделить на 1024, поскольку именно столько единиц младшей величины образуют старшую единицу измерения.
Заключение
Прочитав эту статью, вы получили общее представление о том, что представляет собой мощность алфавита, а также о методах ее расчета. Однако был рассмотрен исключительно математический подход, в котором не учитываются некоторые другие параметры, основным из которых является смысловая нагрузка. Этот аспект является одним из наиболее важных для понимания, поскольку независимо от объема символов, если они не несут никакой информационной ценности, то его ценность равна нулю. Однако рассчитать вес бессмысленного набора символов все равно можно.
Если говорить в общем, то мощность алфавита, как один из терминов информатики, не представляет собой ничего сложного для понимания. Но многие пользователи пренебрегают этим терминов, поскольку считают его бесполезным, однако, на практике все обстоит совершенно иначе. В наши дни пользователи работают преимущественно с электронной информацией, которая со временем может полностью вытеснить печатную, поэтому необходимо иметь представление о том, как эта информация выражается в машинном виде и каким образом она рассчитывается.
Мощность алфавита в информатике
Понятие алфавита в информатике немного отличается от того, что изучают дети в первом классе. Здесь так называют знаковую систему, при помощи которой может быть передано информационное сообщение. Оно состоит из символов — минимально значимых составляющих, которые являются неделимыми. Одним из важнейших терминов в этой области является мощность алфавита.
Описание термина
Понятие мощности алфавита находится в основании изучения информатики. Алфавитом принято называть набор многочисленных символов. Сумма всех их в определённом языке и есть алфавитная мощность. Иными словами, это количество всех символов, входящих в конкретно взятый язык. Сюда входят не только буквы, но и прочие обозначения, в частности:
Это определение считается обобщённым и не принимает во внимание вычисления информационной составляющей сообщения. Она может содержать в себе числа, знаки препинания и прочее. В этом случае прибегают к использованию другого способа. Его суть основывается на том, что любая буква, цифра или знак обладают собственным информационным объемом данных. Компьютер работает с этим информационным кодом и распознает то, что было написано.
Основным постулатом в информатике является тот факт, что устройство разбирает введённую информацию исключительно в двоичном коде в форме нуля и единицы. В итоге получается, что абсолютно любой символ алфавита может быть успешно закодирован при помощи соответствующего подбора этих двух цифровых символов. Самая маленькая последовательность, применяемая при обозначении какой-либо цифры, буквы или другого знака, состоит из двух элементов.
Информационная масса отдельно взятого символа обычно изображается в форме информационной стандартной измерительной единицы, которая называется «бит». Восемь битов становятся равны одному байту.
Отображение символов в двоичном коде
Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:
Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:
Иными словами, если алфавитная мощность равна 8, то вес отдельно взятого символа для двоичного трёхзначного кода составит 3 бита.
Вычисление мощности алфавита
Эта формула была изобретена американским инженером Ральфом Хартли более сотни лет тому назад. Она применяется для работы с равновероятными событиями и используется для определения мощности конкретного буквенного набора, которая обозначается буквой N (информационная масса или объём). n означает численность бит в словесной единице, иными словами, количество знаков внутри двоичного кода. Так, если n равен 1, то N тоже равен 1, при n = 2 N = 4, при n = 3 N = 8, при n = 4 N = 16.
Чтобы сформулировать теорию о численности информации в набранном словосочетании, пользуются формулой I=K*i. В этом случае К обозначает численность всех символов в предложении, а i — это информационная масса символа.
При ответе на вопрос, как найти мощность алфавита, нужно сказать, что в русском языке 33 буквы, поэтому это можно выразить как N = 33. Для сравнения, аналогичный показатель в английском, немецком и французском языках равняется 26, в испанском — 27. Венгерский язык, например, является 40-символьным.
Существует также и клавиатурный язык, куда входят не только буквы, но и дополнительные знаки. Так, в русском языке есть ещё 10 цифр и 11 символов, а также пробел и пара скобок. Их мощность прибавляется к аналогичному буквенному показателю, и на выходе получается N = 33+10+11+1+2=57. В некоторых случаях букву «ё» не выделяют в качестве отдельного самостоятельного символа, и в таком случае полная мощность русского алфавита становится равна 56.
Определение информационного объёма в тексте
Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:
По всем расчётам получается, что мощность компьютерного алфавита составляет 256 различных символов и вариантов. В соответствии с формулой Хартли, N = 256, а i — масса любого из значков в клавиатурном алфавите соответствует одному байту, или восьми битам.
Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.
Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.
В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.
Для удобства их всегда переводят в увеличенные величины — кило-, мега-, гигабайты и прочее. Для их упрощённого обозначения используются специальные сокращения: Кб, Мб, Гб и так далее. 1 Кб равняется 1024 байтам (2 байта в десятой степени), 1 Мб составляет 1024 Кб (2 Кб в десятой степени) и так далее. Исходя из этого, 65250 байт будут составлять 63,72 килобайта.
Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.
При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.
Примеры расчёта мощности
От пользователей или обучающихся в задачах часто требуют научиться определять информационный объём какого-либо сообщения, приняв информационный вес символа за один байт. Так, в отрывке из поэмы Н. Н. Некрасова «Крестьянские дети»:
Я из лесу вышел; был сильный мороз»
будет 67 символов вместе с пробелами, то есть, в соответствии с условиями задания, 67 байт. Их количество умножают на 8 (количество битов в байте), и на выходе получается 536 битов.
Таким образом, зная в теории суть мощности, можно без проблем определять информационный объем различных сообщений.